"Основы финансовой математики" 24

Вид материала

Реферат

Содержание 2.4. Описание методики развития мыслительных способностей учащихся при обучении теме "Основы финансовой математики" ВЦ: Воспитание правильного отношения к общечеловеческим ценностям, высокого чувства гражданского долга.. ОЦ В чем оцениваются проданные товары и оказанные клиентам услуги? Что понимается под финансовой математикой? Данный график позволяет учащимся понять зависимость денег от времени. Тип урока ОЦ: Обеспечить понимание сущности представлений учащихся о процентах через изучение новых понятий и новых задач. Оборудование План изучения нового Учащиеся изучают информационные листы банков, который заранее были положен на каждую парту) Для этого учащиеся снова изучают информационные листы банков, а именно на каких вкладах какие проценты) Представленные величины и формулы предлагается учащимся записать в тетради. Проведем анализ содержания и поиск плана решения задачи. Урок 3 Тема: Временная база финансовых операций. Переменная ставка Это доход от предоставленной в долг суммы, I=FV-PV Осуществляется анализ содержания, и перебираются возможные ситуации, связанные с длительностью начисления процентов Срок кредита Данный график позволяет учащимся лучше осознать модель простых процентов. Записать формулу и взять ее рамочку. Если время финансовой операции выражено в днях, то расчет простых процентов может быть произведен одним из трех возможных вариан Перед тем как учащиеся приступят к самостоятельному решению необходимо провести анализ задачи и поиск плана решения задачи. ... Полное содержание

Подобный материал:

• Данный спецкурс посвящен рассмотрению важных задач современной финансовой математики, 40.94kb.
• Данный спецкурс посвящен основам современной финансовой математики или математической, 39.19kb.
• Программа дисциплины Биномиальные и непрерывные модели финансовой математики Семестр, 23.24kb.
• Рекомендации по повышению финансовой устойчивости на основе анализа Прогнозирование, 545.11kb.
• Лабскер Л. Г. Вероятное моделирование в финансово-экономической области, 15.66kb.
• Зайцев Михаил Владимирович, доктор физико-математических наук, профессор, заведующий, 561.58kb.
• Ifrs 1 Принятие Международных стандартов финансовой отчетности впервые, 382.76kb.
• «Основы математики и информатики», 461.29kb.
• Тема финансы и финансовая деятельность, 963.77kb.
• Программа курсов повышения квалификации учителей математики «теоретические основы, 49.73kb.

2.4. Описание методики развития мыслительных способностей учащихся при обучении теме "Основы финансовой математики"

Урок 1

Тема: Введение в финансовую математику

Тип урока: Лекция с обратной связью

Цели:

РЦ: Развитие умения анализировать полученную информацию и делать собственные выводы.

ВЦ: Воспитание правильного отношения к общечеловеческим ценностям, высокого чувства гражданского долга..

ОЦ: Обеспечить получение учащимися общих представлений о финансовой математике.

1) Учитель заранее предлагает учащимся помочь провести ему лекцию и 2 учащимся дает вопросы для подготовки (что есть деньги и что есть финансы). Лекция проводится с использованием компьютерной поддержки, которая содержит основные факты. Учащиеся записывают эти факты в тетради.

После знакомства с этими понятиями учитель задает классу ряд последовательных вопросов:

• В чем оцениваются проданные товары и оказанные клиентам услуги?
  

Именно деньги являются универсальным измерителем необходимых предприятию ресурсов - сырья и материалов, станков, человеческих ресурсов, информации и т.д. Поэтому планирование и прогнозирование, контроль и оптимизация финансовых потоков являются жизненно важными задачами финансовой службы.

• Что понимается под финансовой математикой?
  
• Чему посвящен курс «Финансовая математика»?
  

2) Затем вводится понятие финансовая математика учителем и на доску выводится график.







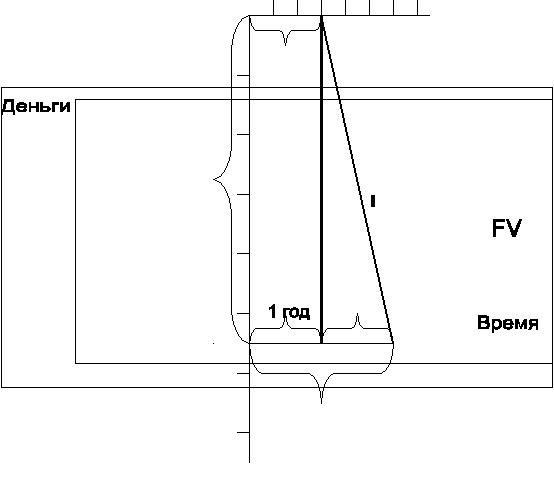
Данный график позволяет учащимся понять зависимость денег от времени.

3) Далее для размышления ученикам ставится проблемный вопрос:

Как фактор времени влияет на финансово-экономические расчеты?

Для того чтобы помочь учащимся ответить на этот вопрос учитель приводит примеры, связанные с обесцениванием денег.

4) рассматривается два утверждения: 1)Рост денег по правилу простых процентов является линейным и подчиняется закону арифметической прогрессии. 2) правило сложных процентов порождает геометрическую прогрессию.

После рассмотрения этих утверждений педагог пытается вступить с учащимися в беседу. А именно интересуется таким вопросом: От чего зависит увеличение капитала при открытии банковского вклада? Какое- то время ученики пытаются ответить самостоятельно без помощи учителя. Если сдвигов, на ответ данного вопроса, не произошло, то учитель выводит следующий рисунок:





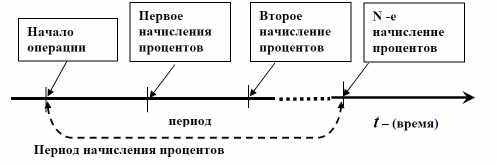
5) Необходимо также уточнить, что курс «основы финансовой математики» предполагает выполнение лабораторных работ на одной из самых популярных программ работающих в операционной среде Windows, сочетающей возможности графического и текстового редакторов с мощной математической поддержкой, позволяющей решать задачи практически любой степени сложности – Excel.

6) На этапе контроля усвоения материала лекции учащимся предлагается работа, состоящая из устных вопросов:

• Чем же мы будем с Вами заниматься на всех последующих уроках? (решением задач на проценты).
  
• Что нам для этого надо знать?
  
• Что надо сделать чтобы увеличить величину на 50%?( достаточно прибавить её половину)
  
• Как найти 20% величины? ( надо найти её пятую часть)
  
• Треть величины это примерно сколько процентов?( это примерно 33%)
  

Итак, на первом вводном занятии (введение в финансовую математику) развитию мышления способствовали ответы на проблемные вопросы учителя. Реализации целей способствовал такой приём, как: помощь со стороны учеников в проведение лекции. Методы, использовавшиеся на уроке: объяснительно-иллюстративный, репродуктивный, частично-поисковый. Виды учебных ситуаций на уроке: автономная деятельность учителя, автономная деятельность учащихся, коллективная работа.


Урок 2

Тема: Основные категории финансово-экономических расчетов

Тип урока: урок введения нового

Цели:

РЦ: Развитие умения анализировать полученную информацию и делать собственные выводы, переносить имеющийся опыт в новые ситуации

ВЦ: Через организацию урока воспитывать активность в учебной работе.

ОЦ: Обеспечить понимание сущности представлений учащихся о процентах через изучение новых понятий и новых задач.

Оборудование: интерактивная доска

I. В организационной части учитель, об объеме изучаемого материала, дает установку на обязательную запись новой информации в тетрадях и дает информацию о значимости темы. Формулирует цель урока: «Разобраться в сущности ключевых понятий темы и в сущности новых ключевых задач», приглашает учащихся принять активное участие в получение новых теоретических и практических сведений о финансовой математике и представляет на интерактивной доске план изучении нового.


План изучения нового:

• Понятийный аппарат финансово-экономических расчетов и их формулы расчетов
  
• Две базовые задачи на финансово-экономические расчеты
  

Запись плана занятия позволит учащимся настроиться на определенный объем работы. Помогает увидеть главное и существенное в теоретических и практических основах изучения темы.

II. Актуализация необходимых знаний в форме устного мини-опроса по следующей системе вопросов:

• Что такое процент? (Процентом (от лат. “pro cento”) числа называется сотая часть этого числа.) Приведите пример.
  
• Как найти % от числа? (Данное число умножается на число процентов и полученный результат делиться на 100.) Приведите пример.
  
• Что значит найти 10 %, 20 % от данного числа? Найдите. Чем это задание отличается от предыдущего? Ответ обоснуйте.
  
• Что значит увеличить данное число на 10 %, на 50 %? Увеличьте число. Ответ обоснуйте. Чем это задание отличается от предыдущего.
  
• В каждой из двух строк данного количеству процентов найти соответствующее число. Ответ обосновать:
  

1) 80% - 3/4, 2/3, 4/5, 7/10.

2) 45% - 9/20, 3/5, 3/10, 5/10.

Комментарий: такой подход к подготовке введения нового (чередование теоретических и практических заданий,. требование обосновать свое решение) способствует осмысленному восприятию теории простых процентов и развитию приемов мыслительной деятельности.

III. Введение нового начинается с показа схеме «виды процентных ставок» которая выводится на интерактивную доску.






Здесь учащиеся должны внимательно посмотреть, что дано на схеме и выделить существенное. Так как цель педагога это понимание учащимися данной темы, а не изложение лекции в чистом виде, то перед тем как учитель сам даст пояснение к каждой процентной ставе необходимо задать ряд наводящих вопросов. Тем самым учащиеся попытаются самостоятельно дать определение каждой процентной ставки.

- Где мы с Вами встречаемся с процентными ставками?

- Что указывает банк на информационном листе при открытии нового вклада? ( Учащиеся изучают информационные листы банков, который заранее были положен на каждую парту).

- Что по Вашему мнению называется фиксированной и плавающей процентной ставкой?( Для этого учащиеся снова изучают информационные листы банков, а именно на каких вкладах какие проценты)

Комментарий: Такой подход в изучении процентной ставки задействует познавательную активность учащихся, т.к. они получают не готовую информацию от учителя, а пытаются разобраться самостоятельно с учетом правильно подобранных вопросов, анализируя и сопоставляя представленные учителем информационные банковские листы и таблицу.

IV. После показа схемы учащиеся попытаются определить четыре величины присутствующие в любой простейшей финансовой операции, при помощи вопросов. Ответ на каждый вопрос педагог будет фиксировать схематично на доске.

- Для достижения какой цели мы открываем вклад в банке?

- Что нужно для увеличения суммы?

Для каждой величины вводится формула. Представленные величины и формулы предлагается учащимся записать в тетради.

VI. Приступая к четвертому вопросу учитель предлагается рассмотреть пример показывающий применение введенных ранее формул.

Пример 1:

Вы заняли сегодня 100 рублей, дав обязательство вернуть к указанной дате 120 рублей. Оценим доходность этой сделки для кредитора величиной процентной ставки r, приняв за единицу времени срок n=1.

Проведем анализ содержания и поиск плана решения задачи.

Анализ содержания задачи:

• О чем идет речь в задаче? (речь идет о займе 100 рублей. )
  
• Какие величины известны? ( текущая стоимость или величина кредита PV=100; срок погашения кредита n=1 год, будущую стоимость или сумма возврата FV=120)
  
• Что необходимо найти? (процентную ставку r)
  
• Какой формулой связаны величины? (r=(FV-PV)/PV)
  
• Можно ли сразу решить задачу или нужны дополнительные условия?
  

Решение: r=(FV-PV)/PV = (120-100)/100 = 20%

Предлагаем учащимся изменить задание предыдущего примера, а именно:


Пример 2:

Вы обратились к кредитору с просьбой о займе 100 руб. (PV) на срок 1 год. Какую сумму сможет получить кредитор по окончании срока займа, при процентной ставке 20%.

Проведем анализ содержания и поиск плана решения задачи.

Анализ содержания задачи:

• О чем идет речь в задаче? (речь идет о займе 100 рублей. )
  
• Какие величины известны? (текущая стоимость или величина кредита PV=100; срок погашения кредита n=1 год, процентная ставка r=20%)
  
• Что необходимо найти? (будущую стоимость или сумму возврата FV)
  
• Какой формулой связаны величины? (r=(FV-PV)/PV)
  
• Можно ли сразу решить задачу или нужны дополнительные условия? (необходимо выразить из формулы величину FV)
  

Решение: решить самостоятельно

Комментарий: Решение задач способствует развитию познавательных мотивов учения, в частности, интереса к предмету как мотива обучения при обсуждении поиска путей решения, а также мотивов сотрудничества при взаимодействии в процессе совместного решения.

Итак, на занятии 2 развитию мышления способствовали ответы на вопросы учителя, выделение главного и существенного, краткая запись задачи. Методы, использовавшиеся на уроке: объяснительно-иллюстративный, репродуктивный.


Урок 3

Тема: Временная база финансовых операций. Переменная ставка

Тип урока: комбинированный урок

Цели:

РЦ: Способствовать развитию умений анализировать, систематизировать, обобщать, составлять план, делать выводы

ВЦ: Через организацию урока воспитывать активность в учебной работе. Формировать умения и навыки применения процентов для количественной характеристики различных явлений окружающего мира.

ОЦ: Сформировать понимание необходимости знаний процентных вычислений для решения задач. Сформировать умение производить процентные вычисления, необходимые для применения в практической деятельности.

Оборудование: интерактивная доска


Ход урока

I. В организационной части учитель дает информацию о значимости темы, об объеме изучаемого материала, записывает тему и план урока на доске, дает установку на обязательную запись читаемого в тетрадях.

План изучения нового:

• Модель простых процентов
  
• Варианты расчета
  
• Переменная ставка
  
• Решение задач на основные формулы
  

Запись плана занятия позволит учащимся настроиться на определенный объем работы.

II. Актуализация необходимых знаний в форме устного мини-опроса по следующей системе вопросов:

• Какие четыре величины присутствуют в любой простейшей финансовой операции ? Напишите на доске их символьное обозначение (время = n; текущая стоимость = PV; будущая стоимость = FV; процентная ставка = r)
  
• Что такое процентные деньги ? Напишите на доске формулу вычисления процентных денег ( Это доход от предоставленной в долг суммы, I=FV-PV)
  
• Что понимается под процентной ставкой? (Это отношение суммы процентных денег, выплачивающихся за определенный период времени, к величине ссуды). Записать формулу процентной ставки ( r=I/PV=(FV-PV)/PV )
  

Комментарий: такой подход к подготовке введения нового способствует осмысленному восприятию теории простых процентов.

III. Введение нового начинается с задачи, конкретный текст которой представляется на интерактивной доске.

Задача1: представим, что кредитор и заемщик договариваются о величине кредита PV (первоначальная денежная сума), в размере годовой процентной ставки r, сроке кредита Т и длительности периода начисления процентов n. Найти наращенную сумму FV.

Осуществляется анализ содержания, и перебираются возможные ситуации, связанные с длительностью начисления процентов

	Обозначение
Величина кредита	PV
Годовая процентная ставка	r
Срок кредита	T
Длительность начисления процентов	n
Наращенная сумма	FV-?

Математическая такая операция может быть представлена в виде модели простых процентов. По этой модели происходит накопление наращенной суммы FV за счет периодического (например, ежегодного) начисления процентных денег I (напомним, что «процентные деньги»- это разность между первоначальной денежной суммой PV и наращенной денежной суммой FV т.е. I=FV-PV ). В соответствии с этим наращенная сумма равна:

к концу первого года – FV₁=PV+I

к концу второго года – FV₂=PV+2*I

к концу n-го года – FV_n=PV+n*I

Комментарий: Учитель вводит учащихся в новую тему с типовой задачи №1, т.к. она содержит ключевую терминологию финансовой математики и ее элементы будут использоваться в последующих типах задач.




IV. Перед тем как записать общую формулу простых процентов, выведем график на интерактивную доску, который показывает накопление первоначальной суммы по схеме простых процентов.


Накопление суммы происходит по схеме простых процентов и образует возрастающую числовую последовательность: FV₁, FV₂,…, FV_n, которая представляет собой арифметическую прогрессию с первым членом PV и разностью прогрессии I=FV-PV.

Данный график позволяет учащимся лучше осознать модель простых процентов.

Для того чтобы убедиться, что модель простых процентов стала понятна учащимся, предлагается обсудить вопрос:

• От каких факторов зависит размер ожидаемой наращенной суммы долга (дохода)? (от величины инвестированной суммы, уровня процентной ставки, срока финансовой операции)
  

V. После осознания сущности процесса наращения учитель записывает модель накопления капитала по схеме простых процентов в общем случае: FV=PV+I=PV+n*PV*I=PV*(1+n*I)………………..(1). Учитывая выражение I=PV*r модель простых процентов можно записать: FV=PV+I=PV+r*PV*n=PV*(1+r*n)=PV*k_n………(2)

Записать формулу и взять ее рамочку.

VI. Приступая ко второму вопросу учитель разбирает следующие варианты расчета которые расшифровываются:

• Временная база ( T )
  

Можно представить по-разному:

- Условно состоящую из 360 дней (в этом случае речь идет об

обыкновенном или коммерческом проценте)

- взять действительное число дней в году 365 или 366 (в этом случае

получаются точные проценты)

• Число дней ссуды ( t )
  

Можно определять по разному:

- Условно, исходя из того, что продолжительность любого целого

месяца составляет 30 дней, а оставшиеся дни от месяца считают

точно, - в результате получают так называемое приближенное число

дней ссуды.

- Используя прямой счет или специальные таблицы порядковых

номеров дней года, рассчитывают фактическое число дней между

датами,- в этом случае получают точное число дней ссуды.

Если время финансовой операции выражено в днях, то расчет простых процентов может быть произведен одним из трех возможных вариантов:

• Обыкновенный проценты с приближенным числом дней ссуды (германская практика расчета)
  

Когда продолжительность года условно принимается за 360 дней, а целого месяца за 30 дней.

• Обыкновенный проценты с точным числом дней ссуды (французская практика расчета)
  

Когда продолжительность года условно принимается за 360 дней, а продолжительность ссуды рассчитывается точно по календарю

• Точные проценты с точным числом дней ссуды (или английская практика)
  

Когда продолжительность года и продолжительность ссуды рассчитывается точно по календарю.

VII. Приступая к 3-му вопросу нового материала, учитель рассматривает сущность по переменной ставке и с помощью задачи №1 совместно с учащимися делает общий вывод в виде формулы (3).

Ставка процентов не является застывшей на вечные времена величиной, поэтому в финансовых операциях, в силу тех или иных причин, предусматриваются дискретно изменяющиеся во времени процентные ставки. Например, наличие инфляции вынуждает собственника денег периодически варьировать процентной ставкой.

В том случае, если на последовательных интервалах начисления процентов n₁, n₂, n₃,…,n_m устанавливаются разные процентные ставки r₁, r₂, r₃,…,r_m, то наращенная сумма может быть определена как

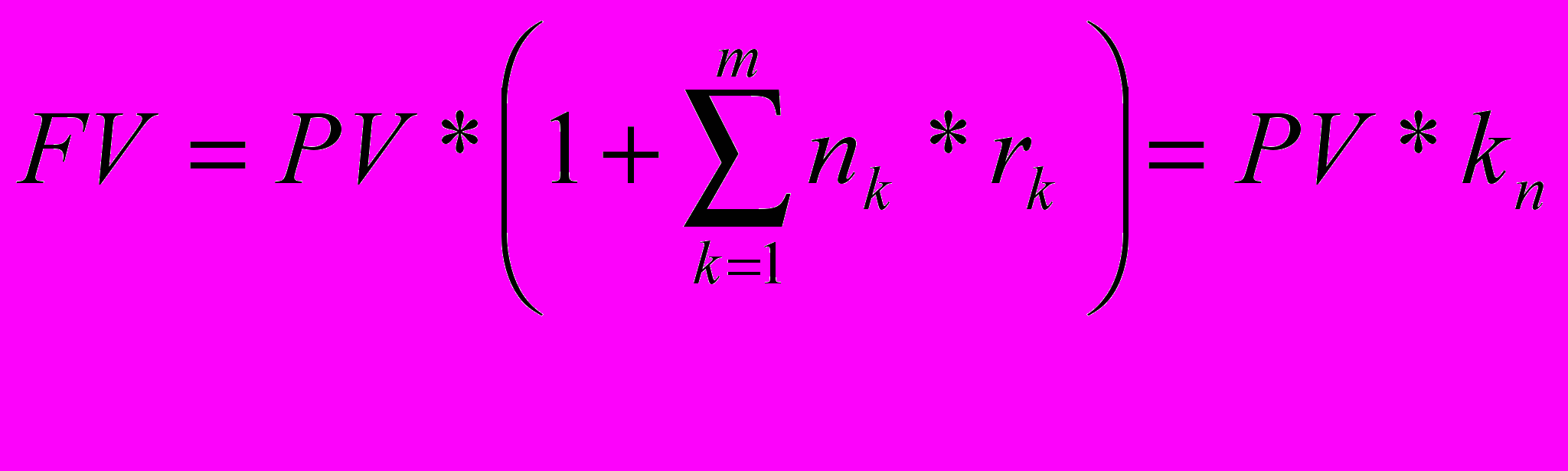где коэффициент наращения (k_n) …….….(3)



VIII. Учитель предлагает найти введенные 3 формулы; проверить их названия и спросить какие типы задач нам предстоит научиться решать.

8.1. Задача 2.

Сумма в размере 2000 рублей выдана в долг на 1 год по схеме простого процента под 10% годовых. Определить проценты и сумму, подлежащую возврату.

Проведем анализ содержания и поиск плана решения задачи.

Анализ содержания задачи:

• О чем идет речь в задаче? (речь идет о кредиторе, который дал деньги в долг на 1 год под 10% годовых)
  
• Какие величины известны? ( текущая стоимость или величина кредита PV=2000; процентная ставка r=10%; срок погашения кредита n=1 год)
  
• Что необходимо найти? (будущую стоимость или сумма возврата FV и проценты или сумма начисленных процентов I )
  
• Какой формулой связаны величины? (формула 2 и формулы I=FV-PV)
  
• Можно ли сразу решить задачу или нужны дополнительные условия? (можно)
  

Решение:

FV=PV*(1+n*r)=2000*(1+1*0.1)=2200

I=FV-PV=2200-2000=200

Таким образом, через год необходимо вернуть общую сумму в размере 2200 рублей, из которой 2000 рублей составляет долг, а 200 рублей –«цена долга (процентные деньги)»

Далее необходимо предложить решить эту задачу другим способом, т.е. математическим.

2. Самостоятельная работа по решению двух задач.
   

Задача 3.

Ссуда в размере 50000 руб. выдана на полгода по простой ставке 14% годовых. Определить наращенную сумму и сумму начисленных процентов

Задача 4.

Определить сумму вклада, которую надо положить в банк сроком на 2 месяца под 10% годовых, чтобы к концу срока получить 110000 рублей.


Чем задачи 3 и 4 отличаются от задачи 2? (в задаче номер 4 известна будущая стоимость FV=110000 руб., и неизвестна текущая стоимость PV,а в задаче 2 наоборот; также в задаче 2 срок равен 1 году, а в задаче 4 срок равен 2 месяца)

Комментарий: В тех случаях, когда срок ссуды менее года, происходит модификация формулы:

а) если срок ссуды выражен в месяцах (М), то величина n выражается в виде дроби: n=M/12…(4)

б) если время выражено в днях (t), то величина n выражается в виде дроби: n=t/T, где t- число дней ссуды, а Т- расчетное число дней в году (временная база)

Перед тем как учащиеся приступят к самостоятельному решению необходимо провести анализ задачи и поиск плана решения задачи.

Анализ содержания задачи:

• О чем идет речь в задаче? (речь идет о вкладчике, который положил деньги в банк на 2 месяца под 10% годовых)
  
• Какие величины известны? ( будущая стоимость FV=110000; процентная ставка r=10%; срок вклада n=2 месяца)
  
• Что необходимо найти? (текущую стоимость или PV )
  
• Какой формулой связаны величины? (формула 2)
  
• Можно ли сразу решить задачу или нужны дополнительные условия? (можно, только необходимо выразить из формулы 2 нужную величину)
  

8.3. Предлагается рассмотреть еще один тип задачи:

Задача 5.

Клиент внес вклад в банк в сумме 1 тыс. руб. сроком на 1 год. Процентная ставка до середины второго квартала составляла 30% годовых, далее до конца третьего квартала -25%, а с начала четвертого квартала- снова 30%. Какую сумму клиент получил в конце года?

Проведем анализ содержания и поиск плана решения задачи:

• Чем эта задача отличается от предыдущих? (тем, что процентная ставка r изменяется во времени)
  
• О чем идет речь в задаче? (речь идет о кладчике, который положил деньги в банк на сроком на 1 год)
  
• Какие величины известны? (текущая стоимость FV=1000; процентная ставка r=30%, r=25%, r=30%; срок вклада n=1 год)
  
• Что необходимо найти? (будущую стоимость или FV )
  
• Какой формулой связаны величины? (формула 3)
  
• Можно ли сразу решить задачу или нужны дополнительные условия? (для этого сначала надо найти коэффициент наращения: до середины второго квартала, затем от середины второго квартала до начала четвертого квартала, потом за четвертый квартал и все эти коэффициенты сложить)
  

IX. В заключительной части урока подводится итог:

- Какого типа задачи мы решали на уроке?

- Назовите формулу простых процентов и обозначения, которые в ней даны?

- Приведите пример задачи, решаемой с помощью формулы простых процентов?


Самоанализ урока

Тип урока: комбинированный урок.

Цели урока следующие:

РЦ: Способствовать развитию навыка анализировать, систематизировать, обобщать, составлять план, делать выводы

ВЦ: Через организацию урока воспитывать активность в учебной работе. Формировать умения и навыки применения процентов для количественной характеристики различных явлений окружающего мира.

ОЦ: Сформировать понимание необходимости знаний процентных вычислений для решения задач. Сформировать умение производить процентные вычисления, необходимые для применения в практической деятельности.

1) Данный урок соответствует календарно-тематическому планированию.

2) Структура урока полностью соответствует логике проведения заявленного типа урока.

3) На протяжении всего урока прослеживалось соблюдение одного из основных принципов дидактической системы – работа над развитием всех учащихся.

4) Отобранное содержание урока, оборудование урока, организация активной мыслительной деятельности учащихся на всех этапах урока, применение словесных, визуальных методов способствовали достижению образовательных целей урока, стимулировали познавательные интересы учащихся.

5) развитию мышления способствовали ответы на вопросы учителя, выделение главного и существенного, краткая запись задачи. Методы, использовавшиеся на уроке: объяснительно-иллюстративный, репродуктивный.

6) Я считаю, что выбранная форма организации учебной деятельности школьников была достаточно эффективной. С моей стороны были соблюдены нормы педагогической этики и такта, культура общения «учитель-ученик».

Полагаю, что использование компьютерных технологий в процессе обучения необходимо, актуально, эффективно, поскольку они имеют ряд преимуществ, а именно:

1. делают процесс обучения продуктивным посредством наглядности;
   
2. мотивируют познавательную деятельность учащихся;
   
3. стимулируют самостоятельную работу учащихся;
   
4. развивают творческие способности учащихся;
   
5. учитель экономит время на уроке для оформления классной доски, наглядного и иллюстрированного материала.
   

Урок 4-5

Тема: Определение срока ссуды и величины процентной ставки

Тип урока: комбинированный урок, урок решения задач

Цели:

РЦ: Способствовать развитию умений анализировать, систематизировать, обобщать, составлять план, делать выводы. Формировать умения и навыки применения процентов для количественной характеристики различных явлений окружающего мира.

ВЦ: Через организацию урока воспитывать активность в учебной работе и самостоятельность.

ОЦ: Углубление и расширение знаний по теме простые проценты. Обеспечение отработки умений. Обучить решению типовых задач на проценты с применением формул простых процентов.

Оборудование: интерактивная доска с записью плана занятия.

План урока:

• Актуализация опорных знаний
  
• Определить формулу срока и величины процентной ставки
  
• Решение задач на нахождение срока и величины процентной ставки
  
• Проверка знаний пройденного материала по теме простые проценты в виде тестирования
  
• Самостоятельное решение задач (парная работа)
  

Запись плана занятия позволит учащимся настроиться на определенный объем работы.

Ход урока

I. В организационной части учитель дает информацию о значимости темы, об объеме изучаемого материала, записывает тему и план урока на доске, дает установку на обязательную запись читаемого в тетрадях.

II. Актуализация необходимых знаний в форме устного мини-опроса по следующей системе вопросов:

• Какие четыре величины присутствуют в любой простейшей финансовой операции ? Напишите на доске их символьное обозначение (время = n; текущая стоимость = PV; будущая стоимость = FV; процентная ставка = r)
  
• Назовите формулу для наращения вложенной суммы по схеме простых процентов ( FV=PV*(1+r*n) )
  
• Назовите формулу для наращения вложенной суммы, если процентная ставка r изменяется во времени ()
  

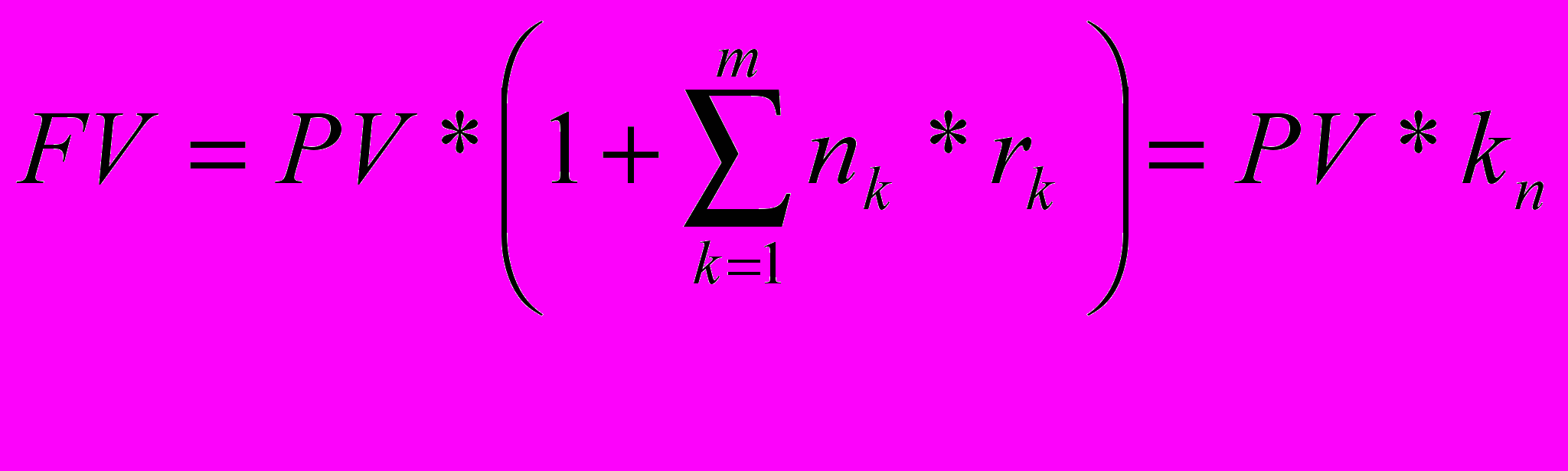Комментарий: Актуализация знаний в форме перечисленных выше вопросов способствует осмысленному восприятию теории простых процентов.

III. Введение новых формул начинается с информационного сообщения учителя с использованием блок схемы.








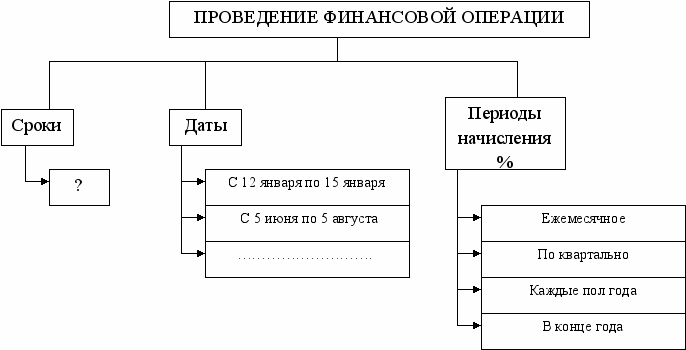
“Как правило, при проведении финансовых операций обязательно фиксируются сроки, даты, периоды начисления процентов, так как фактор времени (как мы уже отмечали) в финансово-коммерческих расчетах играет важную роль...

Однако достаточно часто возникают ситуации, когда срок финансовой операции в условиях конкретной финансовой сделки не может быть оговорен заранее, а когда определяется при достижении какой-то цели финансовой операции (конечной или промежуточной)….

Подобным же образом может обстоять дело и с определением величины процентной ставки. Так, например, на начальном этапе заключения коммерческой сделки нас могут интересовать только величины вложенных (PV) и полученных сумм (FV). В тоже время при анализе эффективности этой сделки возникает вопрос степени ее доходности”…

Эти величины могут быть легко определены из введенных ранее формул определения наращения вложенной суммы по схеме простых процентов.

Срок финансовой операции может быть определен как:

при определении срока в годах - n=(FV-PV)/(PV*r)…………..(1)

при определении срока в днях - t=[(FV-PV)/(PV*r)]*T………(2)

Процентная ставка может быть определена как:

r=(FV-PV)/(PV*n)=[(FV-PV)/(PV*t)]*T………(3)

Комментарий: Сопоставление формул процентной ставки и сроков по годам и дням помогает осознать сущность вводимой информации.

VI. Отработка новых знаний осуществляется через решение 3-х задач по трем введенным формулам. Учитель последовательно представляет текст задачи на интерактивной доске, обсуждает содержание, выявляет совместными усилиями формулу для ее решения и записывает решение.

Задача 1.

За какое время может быть накоплена сумма в 2000 долларов, если сегодня мы можем оформить депозитный вклад 1000 долларов под 10% годовых.

Проведем анализ содержания и поиск плана решения задачи.

Анализ содержания задачи:

• О чем идет речь в задаче? (речь идет о вкладчике, который положил деньги в банк под 10% годовых)
  
• Какие величины известны? (текущая стоимость PV=1000; будущая стоимость FV=2000; процентная ставка r=10%)
  
• Что необходимо найти? (срок накопления капитала (n) в размере 2000 )
  
• Какой формулой связаны величины? (формула 1)
  
• Можно ли сразу решить задачу или нужны дополнительные условия…?
  

Решение: п = (FV-PV)/(PV *n)= (2ООО-1ООО)/(1ООО*О,1) = 10 лет


Задача 2.

На сколько дней можно дать в долг 1000 долларов, исходя из 8% годовых, если возвращенная сумма должна составлять 1100 долларов.

Проведем анализ содержания и поиск плана решения задачи.

Анализ содержания задачи:

• О чем идет речь в задаче? (речь идет о кредиторе, который дал деньги в долг на 1 год под 8% годовых)
  
• Какие величины известны? (текущая стоимость PV=1000; будущая стоимость FV=1100; процентная ставка r=8%)
  
• Что необходимо найти? (срок накопления капитала (n) в размере 1100 )
  
• Отличается ли эта задача от предыдущей и если да то чем? (отличается тем. Что срок финансовой операции определен в днях)
  
• Какой формулой связаны величины? (формула 2)
  
• Можно ли сразу решить задачу или нужны дополнительные условия…?
  

Решение: t= [(FV-PV)/(PV*r)] *T= (1100-1000)/(1000*0.08)*360 =450 дней

Задача 3.

В контракте предусматривается погашение обязательств через 120 дней в сумме 1200 долларов, при первоначальной сумме долга 1150 долларов. Определить доходность операции для кредитора в виде процентной ставки.

Проведем анализ содержания и поиск плана решения задачи.

Анализ содержания задачи:

• О чем идет речь в задаче? (речь идет о кредиторе, который дал деньги в долг на 120 дней)
  
• Какие величины известны? (текущая стоимость PV=1150; будущая стоимость FV=1200; срок n=120 дней)
  
• Что необходимо найти? (процентную ставку r )
  
• Какой формулой связаны величины? (формула 3)
  
• Можно ли сразу решить задачу или нужны дополнительные условия…?
  

Комментарий: Перед решением необходимо задать следующий уточняющий вопрос: Используя, какую формулу, будем рассчитывать годовую процентную ставку? (Рассчитываем годовую процентную ставку, используя формулу «обыкновенного процента», поскольку в условиях сделки нет ссылки на точный процент)

Решение: r=(FV-PV)/(PV*n)=[(FV-PV)/(PV*t)]*T =[(1200- 1150)/(1150* 120)] * 360 = 0.13

Задача 4. (Решите самостоятельно)

Банк выдал ссуду в размере 100000 рублей сроком:

а) на 5 месяцев: б) на 3 месяца.

Какими должны быть процентные ставки с тем. чтобы доход банка (не зависимо от срока ссуды) составил 120000 рублей?

VII. Для понимания уровня сформированности умений решать типовые задачи по теме простые проценты учащимся предлагается пройти тест. (см. приложение 1).

Характеристика теста

Тема: простые проценты

Цель: сформировать умение решать типовые задачи по теме простые проценты.

Время прохождения и критерии оценивания: на тест отводится 23 мин.; результаты теста оцениваются по следующей категории: удовлетворительно, хорошо, отлично.

Инструкции по выполнению: Тест состоит из 11 вопросов, в каждом вопросе представлено четыре варианта ответа, необходимо выбрать правильный вариант ответа.

VIII. После осознания правил вычисления простых процентов учитель предлагает выполнить самостоятельную работу по решению задач на простые проценты в парах на оценку. (список задач смотри в приложении 2)


Самоанализ урока

Тип урока: комбинированный урок, урок решения задач.

Цели урока следующие:

РЦ: Способствовать развитию умений анализировать, систематизировать, обобщать, составлять план, делать выводы. Формировать умения и навыки применения процентов для количественной характеристики

ВЦ: Через организацию урока воспитывать активность в учебной работе и самостоятельность.

ОЦ: Углубление и расширение знаний по теме простые проценты. Обеспечение отработки умений. Обучить решению типовых задач на проценты с применением формул простых процентов.

1) Данный урок соответствует календарно-тематическому планированию, является заключительным в изучении темы «Простые проценты».

2) Структура урока полностью соответствует логике проведения заявленного типа урока.

3) На протяжении всего урока прослеживалось соблюдение одного из основных принципов дидактической системы – работа над развитием всех учащихся.

4) Отобранное содержание урока, оборудование урока, организация активной мыслительной деятельности учащихся на всех этапах урока, применение словесных, визуальных методов способствовали достижению образовательных целей урока, стимулировали познавательные интересы учащихся.

5) развитию мышления способствовало выполнение самостоятельной работы, ответы на вопросы учителя по ходу урока, предложение учителя записать решение задачи. Методы, использовавшиеся на уроке: объяснительно-иллюстративный, частично-поисковый, репродуктивный.

6) Я считаю, что выбранная форма организации учебной деятельности школьников была достаточно эффективной. С моей стороны были соблюдены нормы педагогической этики и такта, культура общения «учитель-ученик».

Полагаю, что использование компьютерных технологий в процессе обучения необходимо, актуально, эффективно, поскольку они имеют ряд преимуществ, а именно:

6. делают процесс обучения продуктивным посредством наглядности;
   
7. мотивируют познавательную деятельность учащихся;
   
8. стимулируют самостоятельную работу учащихся;
   
9. развивают творческие способности учащихся;
   
10. учитель экономит время на уроке для оформления классной доски, наглядного и иллюстрированного материала.