Geum.ru

Робоча навчальна програма навчальної дисципліни " Вища математика " (за кредитно-модульною системою) Напрям: 0925 "Автоматизація та комп’ютерно-інтегровні системи"

Вид материалаДокументы

Содержание


2. Зміст навчальної дисципліни
3. Навчально-методичні матеріали з дисципліни
1. Пояснювальна записка
1.2. Завдання вивчення навчальної дисципліни
1.3. Місце навчальної дисципліни в системі професійної підготовки фахівців
1.4. Інтегровані вимоги до знань і умінь з навчальної дисципліни.
1.5. Інтегровані вимоги до знань і умінь з навчальних модулів
Знати: – типи диференціальних рівнянь та методи їх розв’язання;Вміти
1.6. Міждисциплінарні зв’язки навчальної дисципліни
2. Зміст навчальної дисципліни
Модуль №1 „ Елементи лінійної та векторної алгебри”
Модуль №2 „ Елементи аналітичної геометрії”
Модуль №4 „ Комплексні числа. Диференціальне числення функції кількох змінних”
Модуль №5 „ Інтегральне числення функції однієї змінної”
Модуль №7 „ Ряди”
Усього за 3 семестр
Модуль №10 „ Операційне числення”
Усього за модулем №10
Усього за модулем №11
Усього за модулем №12
...
Полное содержание
Подобный материал:
  1   2   3   4   5   6


НАЦІОНАЛЬНИЙ АВІАЦІЙНИЙ УНІВЕРСИТЕТ


Інститут електроніки та систем управління

Факультет систем управління


Кафедра вищої та обчислювальної математики


ЗАТВЕРДЖУЮ Індекс Р01 – 8.092502 – 13 Проректор з навчальної роботи

__________________ М.Кулик

“_____”______________2005р


РОБОЧА НАВЧАЛЬНА ПРОГРАМА


навчальної дисципліни

“ Вища математика ”

(за кредитно-модульною системою)


Напрям: 0925 “Автоматизація та комп’ютерно-інтегровні системи”


Спеціальність: 6.092500 – “ Комп’ютерно-інтегровані технологічні процеси та

виробництва”


Курс – 1, 2 Семестр 1, 2, 3, 4

Лекції – 210 год.

Практичні заняття – 210 год. Іспит –1, 2,3 семестри

Самостійна робота – 262 год. Диференційовний залік – 4 семестр

Індивідуальна робота – 20 год.

Всього годин – 702 год.

Контрольні роботи 4 (1, 2, 3, 4 семестри)




Київ 2005


Робоча навчальна програма складена на основі робочого навчального плану № РБ-3-502/01 напряму 0925 “Автоматизація та комп’ютерно-інтегровні системи” спеціальності 6.092500 – “ Комп’ютерно-інтегровані технологічні процеси та виробництва”, навчальної програми з дисципліни “Вища математика” Н– 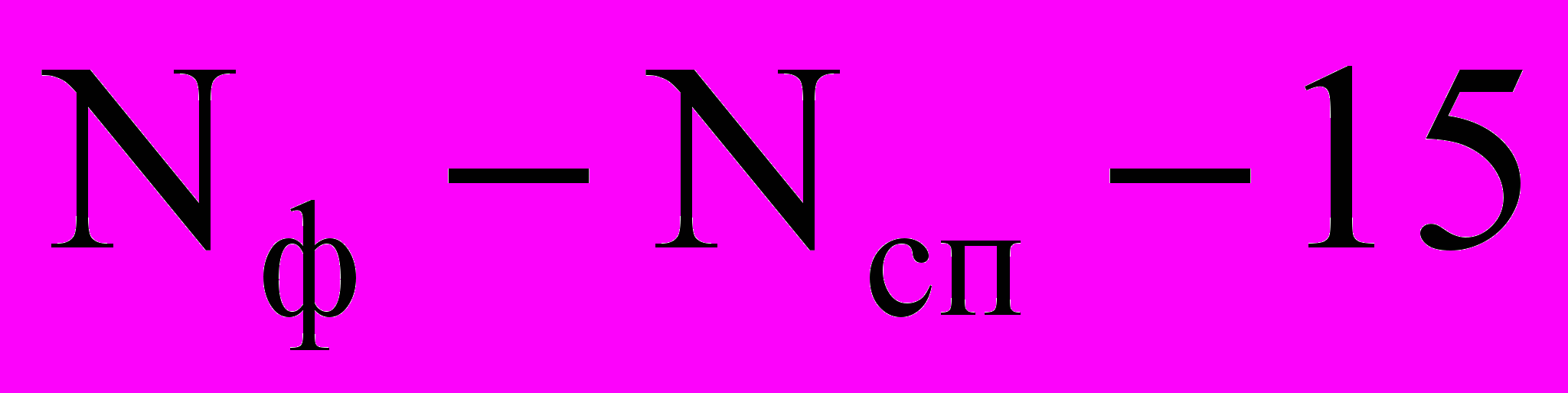, затвердженої 11.04.97 р. та перезатвердженої для спеціальності 6.092500 – “ Комп’ютерно-інтегровані технологічні процеси та виробництва” 23.06.05 р., “Тимчасового Положення про організацію навчального процесу за кредитно-модульною системою (в умовах педагогічного експерименту)” та “Тимчасового Положення про рейтингову систему оцінювання”, затверджених наказом ректора від 15.06.2004 №122/од.


Робочу навчальну програму склав

к.ф.–м. н., доц. В.Репета


Робоча навчальна програма розглянута на засіданні кафедри вищої та обчислювальної математики, протокол № від 2005 р.


Завідувач кафедри

д.ф.-м. н., проф. В.Денисюк


Робоча навчальна програма узгоджена з випусковою кафедрою комп’ютерно-інтегрованих комплексів спеціальності 6.092500 – “ Комп’ютерно-інтегровані технологічні процеси та виробництва”


Завідувач випускової кафедри


_______________ В. Синєглазов

“____”___________2005 р.


Робоча навчальна програма обговорена та схвалена на засіданні науково-методично-редакційної комісії факультету систем управління, протокол № від

Голова НМРК___________________________________ Ю.Безкоровайний


“згоден”

Декан факультету систем управління

________________ О.П. Кривоносенко

“___”_________2005 р.


ЗМІСТ


Вступ ............................................................................................................

1. Пояснювальна записка ............................................................................

1.1. Мета викладання навчальної дисципліни ................................................

1.2. Завдання вивчення навчальної дисципліни ..............................................

1.3. Місце навчальної дисципліни в системі професійної підготовки

фахівця .........................................................................................................

1.4. Інтегровані вимоги до знань і умінь з навчальної дисципліни ..............

1.5. Інтегровані вимоги до знань і умінь з навчальних модулів ...................

1.6. Міждисциплінарні зв’язки навчальної дисципліни .................................

2. Зміст навчальної дисципліни .................................................................

2.1. Тематичний план навчальної дисципліни ................................................

2.2. Проектування дидактичного процесу з видів навчальних занять ..............

2.2.1. Лекційні заняття, їх тематика і обсяг .....................................................

2.2.2. Практичні заняття, їх тематика і обсяг ..............................................

2.2.3. Індивідуальна робота ...............................................................................

2.2.3.1. Контрольні роботи ...............................................................................

2.2.3. Самостійна робота студента і контрольні заходи .................................

2.2.4. Графік проведення модульних контрольних робіт...............................

3. Навчально-методичні матеріали з дисципліни ..................................

3.1. Основна та додаткова література...............................................................

4. Рейтингова система оцінювання набутих студентом знань та вмінь

4.1 Основні терміни, поняття, означення .......................................................

4.2. Рейтингова система оцінювання набутих студентом знань та вмінь ....
4

4

4

4


4

4

4

8

8

8

8

10

16

22

23

23

28

28

28


29

31



ВСТУП


Однією з необхідних умов організації навчального процесу за кредитно-модульною системою є наявність робочої навчальної програми з кожної дисципліни, виконаної за модульно-рейтинговими засадами і доведеної до відома викладачів та студентів.

Рейтингова система оцінювання (РСО) є невід’ємною складовою робочої навчальної програми і передбачає визначення якості виконаної студентом усіх видів аудиторної та самостійної навчальної роботи та рівня набутих ним знань та вмінь шляхом оцінювання в балах результатів цієї роботи під час поточного, модульного та семестрового контролю, з наступним переведенням оцінки в балах у оцінки за традиційною національною шкалою та шкалою ECTS (European Credit Transfer System).


1. ПОЯСНЮВАЛЬНА ЗАПИСКА


1.1. Мета викладання навчальної дисципліни

Мета викладання навчальної дисципліни полягає в тому, щоб навчити студентів володінню відповідним математичним апаратом, який повинен бути достатнім для опрацьовування математичних моделей, пов’язаних з подальшою практичною діяльністю фахівців.


1.2. Завдання вивчення навчальної дисципліни

Завданнями вивчення навчальної дисципліни є:

– прищепити необхідні теоретичні знання та вміння розбиратися у математичному

апараті;
  • дати первинні навички математичного дослідження прикладних задач;
  • розвиток математичного мислення;
  • виробити навички самостійного вивчення наукової літератури з математики та її застосування.


1.3. Місце навчальної дисципліни в системі професійної підготовки фахівців

Загальний курс вищої математики є фундаментом математичної освіти спеціаліста. В стандарт технічної освіти розвинутих країн як обов’язкова складова входить добре володіння математичним апаратом. Вивчення математики пов’язане з опануванням інших загальнонаукових та спеціальних дисциплін і з подальшою діяльністю випускників вузу в якості спеціалістів.


1.4. Інтегровані вимоги до знань і умінь з навчальної дисципліни.

В результаті вивченні дисципліни студент повинен знати:
  • основні означення, теореми, правила та їх практичне застосування;
  • доведення найбільш важливих теорем, які лежать в основі методів, що вивчаються.

Студент повинен уміти:
  • користуватися методами вищої математики прививченні загальнонаукових та спеціальних дисциплін;
  • застосовувати математичні методи при розв’язуванні практичних задач з використанням обчислювальної техніки і нормативної літератури.


1.5. Інтегровані вимоги до знань і умінь з навчальних модулів

Навчальний матеріал дисципліни структурований за модульним принципом і складається з дванадцяти навчальних модулів.

1.5.1. У результаті засвоєння навчального матеріалу навчального модуля №1 „Елементи лінійної та векторної алгебри” студент повинен:

Знати:

– властивості та методи обчислення визначників;

– методи розв’язання систем лінійних алгебраїчних рівнянь;

– властивості та обчислення скалярного, векторного та мішаного добутків

векторів.

Вміти:

– обчислювати визначники;

– виконувати дії з матрицями;

– знаходити ранг матриці;

– знаходити обернену матрицю;

– розв’язувати СЛАР методом Крамера, матричним методом, методом Гаусса;

– аналізувати сумісність СЛАР;

– розкладати вектор за базисом;

– застосовувати скалярний, векторний та мішаний добутки до розв’язання

геометричних задач.


1.5.2. У результаті засвоєння навчального матеріалу навчального модуля №2

„ Елементи аналітичної геометрії ” студент повинен:

Знати:

– способи задання прямої та площини;

– різні форми рівняння прямої на площині;

– рівняння площини, прямої у просторі;

– рівняння кривих та поверхонь другого порядку.

Вміти:

– розв’язувати метричні задачі на площині і у просторі.


1.5.3. У результаті засвоєння навчального матеріалу навчального модуля №3 „ Диференціальне числення функції однієї змінної ” студент повинен:

Знати:

– похідні основних елементарних функцій і загальні правила відшукання похідних.

– правила диференціювання;

– основні формули диференціального числення

– загальну схему побудови графіка функції;

– теореми про границі, важливі границі.

Вміти:

– обчислювати границі;

– досліджувати функції на неперервність;

– знаходити похідні різних порядків функцій;

– будувати графіки функцій.


1.5.4. У результаті засвоєння навчального матеріалу навчального модуля №4 „ Комплексні числа. Диференціальне числення функції кількох змінних ” студент повинен:

Знати:

– форми запису комплексного числа;

– правила виконання дій з комплексними числами;

– частинні похідні;

– необхідну і достатню умови екстремуму функції двох змінних.

– формули дотичної площини та нормалі до поверхні, похідної за напрямом, градієнта.


Вміти:

– знаходити частинні похідні першого та вищих порядків явно заданої функції;

– досліджувати функцію двох змінних на екстремум;

– виконувати дії з комплексними числами.

1.5.5. У результаті засвоєння навчального матеріалу навчального модуля №5 „ Інтегральне числення функції однієї змінної ” студент повинен:

Знати:

– таблицю невизначених інтегралів;

– методи інтегрування;

Вміти:

– знаходити невизначені, визначені та невласні інтеграли;

– застосовувати визначені інтегралі до фізичних та геометричних задач.

1.5.6. У результаті засвоєння навчального матеріалу навчального модуля №6 „ Диференціальні рівняння ” студент повинен:

Знати:

– типи диференціальних рівнянь та методи їх розв’язання;

Вміти:

– знаходити загальний, частинний розв’язки диференціального рівняння та системи диференціальних рівнянь;

– складати диференціальне рівняння для конкретної фізичної задачі.


1.5.7. У результаті засвоєння навчального матеріалу навчального модуля №7 „ Ряди ” студент повинен:

Знати:

– типи числових та функціональних рядів;

– достатні ознаки збіжності знакододатних числових рядів;

– розвинення в степеневий ряд основних елементарних функцій.

Вміти:

– досліджувати числові ряди на збіжність;

– знаходити область збіжності функціональних рядів.

– розкладати функції у степеневий ряд;

– застосовувати ряди до наближених обчислень.

– розкладати функцію у ряд Фур’є для різних випадків задання функції.

1.5.8. У результаті засвоєння навчального матеріалу навчального модуля №8 „ Кратні, криволінійні та поверхневі інтеграли. Елементи теорії поля ” студент повинен:

Знати:

– означення, властивості та обчислення кратних, криволінійних та поверхневих

інтегралів;

– системи координат на площині і у просторі;

– формулу заміни змінних у кратному інтегралі;

– типи скалярних і векторних полів, їхні диференціальні і інтегральні характеристи-ки.

Вміти:

– обчислювати інтеграли;

– знаходити характеристики скалярного і векторного полів ( похідну за напрямом,

градієнт, дивергенцію, ротор, потік, роботу, циркуляцію, потенціал).

1.5.9. У результаті засвоєння навчального матеріалу навчального модуля №9 „ Теорія функції комплексної змінної ” студент повинен:

Знати:

– основні елементарні функції комплексної змінної;

– формули диференціювання та інтегрування функції комплексної змінної;

– ряди Тейлора і Лорана, ізольовані особливі точки, лишки.

Вміти:

– виділяти дійсну і уявну частини функції;

– диференціювати та інтегрувати функції;

– розкладати функції у ряд Лорана;

– застосовувати лишки до знаходження інтегралів.

1.5.10. У результаті засвоєння навчального матеріалу навчального модуля №10

„ Операційне числення ” студент повинен:

Знати:

– зображення основних елементарних функцій;

– властивості оригіналів і зображень.

Вміти:

– знаходити зображення оригіналів та оригіналу за зображенням;

– застосовувати перетворення Лапласа до розв’язування прикладних задач.


1.5.11. У результаті засвоєння навчального матеріалу навчального модуля №11 „ Чисельні методи ” студент повинен:

Знати:

– основні методі розв’язання нелінійних рівнянь, визначених інтегралів,

диференціальних рівнянь;

– алгоритм побудови інтерполяційного многочлена Лагранжа;

– обгрунтування методу найменших квадратів.

Вміти:

– знаходити наближі розв’язки нелінійних рівнянь;

– обчислювати визначені інтеграли за допомогою квадратурних формул;

– будувати інтерполяційного многочлена Лагранжа;

– будувати лінійний та кубічний сплайни;

– апроксимувати експериментальні дані лінійною та квадратичною функціями;

– інтегрувати диференціальні рівняння першого порядку методами Ейлера та Рунге-Кутта.


1.5.12. У результаті засвоєння навчального матеріалу навчального модуля №12 „ Теорія ймовірностей та елементи математичної статистики ” студент повинен:

Знати:

– різні означення ймовірностей;

– формули для обчислення ймовірностей;

– функції розподілу та їхні властивості;

– числові характеристики випадкових величин;

– основні закони розподілу випадкових величин;

– основні поняття і задачі математичної статистики.

Вміти:

– обчислювати ймовірності випадкових подій;

– знаходити числові характеристики випадкових величин;

– будувати закони розподілу випадкових величин;

– оцінювати невідомі параметри;

– проводити перевірку статистичних гіпотез.


1.6. Міждисциплінарні зв’язки навчальної дисципліни

В умовах технічного вузу курс вищої математики є одним з основних, визначальних як всього процесу навчання, так і подальшої практичної діяльності спеціаліста. Для вивчення цього курсу необхідні знання математики в об’ємі середньої школи.

Вища математика є базовою дисципліною для вивчення дисциплін “Теорія автоматичного управління”, “Електротехніка і електромеханіка”, “Основи теорії управління польотом”, “Теорія інформації”, “Основи переробки та передачі інформації”, та іншими, які зв’язують математику з технічними науками і дозволяють проводити аналіз технічних процесів і розв’язувати практичні задачі сучасними методами.

Міждисциплінарні зв’язки навчальної дисципліни ілюструються рисунком.


























. . . . . . . . . . . .




Знання та вміння, отримані під час вивчення даної навчальної дисципліни, будуть використані під час вивчення переважної більшості наступних дисциплін професійної та практичної підготовки фахівця.


2. Зміст навчальної дисципліни

2.1. Тематичний план навчальної дисципліни

Таблиця 2.1

№

пор.
Назва теми
Обсяг навчальних занять

(год.)

Усього
Лекції
Прак-тичні
СРС
Інд. роб.

1
2
3
4
5
6
7

1 семестр

Модуль №1 „ Елементи лінійної та векторної алгебри”

1.1
Елементи лінійної алгебри
32
10
10
12



1.2
Елементи векторної алгебри
17
4
6
7



1.3
Модульна контрольна робота №1
3
2



1



Усього за модулем №1
52
16
16
20



Модуль №2 „ Елементи аналітичної геометрії”

2.1
Пряма на площині та у просторі.

26
8
8
10



2.2
Криві та поверхні другого порядку
17
4
6
7



2.3
Модульна контрольна робота №2
3
2



1



Усього за модулем №2
46
14
14
18



Модуль №3 „ Диференціальне числення функції однієї змінної ”

3.1
Теорія границь
31
8
10
9
4

3.2
Похідна та її застосування
34
11
11
11
1

3.3
Контрольна робота №1
6





6



3.4
Модульна контрольна робота №3
3
2



1



Усього за модулем №3
74
21
21
27
5

Усього за 1 семестр
172
51
51
65
5

2 семестр

Модуль №4 „ Комплексні числа. Диференціальне числення функції кількох змінних”

4.1
Комплексні числа
6
2
2
2



4.2
Диференціальне числення функції кількох змінних
34
10
12
12



4.3
Модульна контрольна робота №4
3
2



1



Усього за модулем №4
43
14
14
15



Модуль №5 „ Інтегральне числення функції однієї змінної”

5.1
Невизначений інтеграл
35
10
12
11
2

5.2
Визначений інтеграл та його застосування.
32
10
10
10
2

5.3
Контрольна робота №2
6





6



5.4
Модульна контрольна робота №2
3
2



1



Усього за модулем №5
76
22
22
28
4

Модуль №6 „ Диференціальні рівняння ”

6.1
Диференціальні рівняння першого порядку
15
4
4
6
1

6.2
Диференціальні рівняння вищих порядків. Системи диференціальних рівнянь

41
12
14
15



6.3
Модульна контрольна робота №3
3
2



1



Усього за модулем №6
59
18
18
22
1

Усього за 2 семестр
178
54
54
65
5

3 семестр

Модуль №7 „ Ряди”

7.1
Числові ряди
15
4
6
5



7.2
Функціональні ряди
34
10
10
12
2

7.3
Модульна контрольна робота №7
3
2



1



Усього за модулем №7
52
16
16
18
2

Модуль №8 „ Кратні, криволінійні та поверхневі інтеграли. Елементи теорії поля”

8.1
Кратні інтеграли
22
6
6
8
2

8.2
Криволінійні інтеграли
13
4
4
5



8.3
Поверхневі інтеграли та елементи теорії поля
30
8
10
11
1

8.4
Контрольна робота №3
6





6



8.5
Модульна контрольна робота №8
3
2



1



Усього за модулем №8
74
20
20
31
3

Модуль №9 „ Теорія функції комплексної змінної”

9.1
Функції комплексної змінної

21
6
8
7



9.2
Ряди в комплексній області

24
7
7
10



9.3
Модульна контрольна робота №3
3
2



1



Усього за модулем №9
48
15
15
18



Усього за 3 семестр
174
51
51
67
5

4 семестр

Модуль №10 „ Операційне числення”

10.1
Оригінал та зображення за Лапласом.
23
6
8
9



10.2
Застосування перетворення Лапласа
14
4
4
4
2

10.3
Модульна контрольна робота №10
3
2



1



Усього за модулем №10
40
12
12
14
2

Модуль №11 „ Чисельні методи”

11.1
Наближене розв’зування рівнянь та інтегралів
23
6
8
9



11.2
Інтерполяція і наближення функцій
18
6
6
6



11.3
Модульна контрольна робота №11
3
2



1



Усього за модулем №11
44
14
14
16



Модуль №12 „ Теорія ймовірностей та елементи математичної статистики”

12.1
Випадкові події

23
6
8
7
2

12.2
Випадкові величини

43
14
14
14
1

12.3
Елементи математичної статистики
19
6
6
7



12.4
Контрольна робота №4
6





6



12.5
Модульна контрольна робота №12
3
2



1



Усього за модулем №12
94
28
28
35
3

Усього за 4 семестр
178
54
54
65
5

Усього за навчальною дисципліною
702
210
210
262
20



2.2. Проектування дидактичного процесу з видів навчальних занять

2.2.1. Лекційні заняття, їх тематика і обсяг