Geum.ru

Робоча навчальна програма навчальної дисципліни " Вища математика " (за кредитно-модульною системою) Напрям: 0925 "Автоматизація та комп’ютерно-інтегровні системи"

Вид материалаДокументы

Содержание


Перший семестр
Другий семестр
Модуль №7 „ Ряди”
Модуль №10 „ Операційне числення”
Усього за модулем №10
Усього за модулем №11
Усього за модулем №12
Подобный материал:
1   2   3   4   5   6



2.2.2. Практичні заняття, їх тематика і обсяг

Таблиця 2.3

№

пор.
Назва теми
Обсяг навчальних занять (год.)

Практ.

заняття
СРС

1
2
3
4

Перший семестр

Модуль №1 „ Елементи лінійної та векторної алгебри”

1.1
Визначники 2-го і 3-го порядків. Властивості визначників. Мінори та алгебраїчні доповнення.
2
2

1.2
Загальне означення визначника 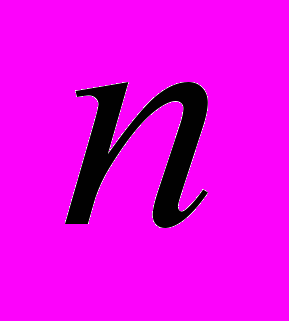–го порядку. Обчислення визначників. Застосування визначників до дослідження СЛАР. Формули Крамера.
2
1

1.3
Матриці, дії з ними. Обернена матриця. Матричні рівняння. Ранг матриці.
2
1

1.4
Система лінійних алгебраїчних рівнянь, її сумісність, дослідження сумісності системи за допомогою рангу матриць. Теорема Кронекера-Капеллі. Методи розв’язання СЛАР (Крамера, матричний, Гаусса). Однорідні системи.
2
2

1.5
Невизначені системи та їх розв’язання. Однорідні системи лінійних алгебраїчних рівнянь. Власні числа та власні вектори матриці.
2
1

1.6
Вектори, загальні означення, лінійні дії з векторами. Лінійна залежність і незалежність векторів. Базис. Проекція вектора на вісь. Системи координат на площині і в просторі

( ПДСК, полярна система координат). Метод координат. Вектори в ПДСК( координати, довжина, напрямні косинуси). Поділ відрізка у даному відношенні.
2
2

1.7
Скалярний добуток. Означення, властивості, обчислення, координатна форма. Геометричний зміст. Умова перпендикулярності двох векторів.
2
2

1.8
Векторний та мішаний добутки векторів Означення, властивості, обчислення, координатна форма. Геометричний зміст. Умова компланарності трьох векторів.
2
1

Усього за модулем №1
16
12

Модуль №2 „ Елементи аналітичної геометрії.”

2.1
Пряма на площині. Загальне рівняння прямої, неповні рівняння. Канонічне та параметричні рівняння прямої. Пряма, яка проходить через дві задані точки. Рівняння прямої у відрізках на осях.

2
2

2.2
Пряма з кутовим коефіцієнтом. Кут між двома прямими, умови паралельності і перпендикулярності двох прямих. Нормальне рівняння прямої. Відстань від точки до прямої
2
2

2.3
Площина і пряма у просторі . Способи задання площини. Види рівнянь площини. Пряма у просторі.
2
1

2.4
Площина і пряма у просторі. Взаємне розташування прямої і площини. Кут між площинами, прямими, площиною та прямою. Умови паралельності і перпендикулярності.
2
1

2.5
Криві другого порядку. Коло, еліпс. Їхні властивості, канонічні рівняння.
2
2

2.6
Криві другого порядку. Гіпербола, парабола. Їхні властивості, канонічні рівняння
2
2

2.7
Поняття поверхні другого порядку. Циліндричні, конічні поверхні, поверхні обертання. Канонічні рівняння.
2
1

Усього за модулем №2
14
11

Модуль №3 „ Вступ до математичного аналізу . Диференціальне числення функції однієї змінної ”

3.1
Поняття послідовності. Границя послідовності. Теореми про границі. Число e. Визначені та невизначені вирази. Обчислення границь.
2
1

3.2
Поняття функції. Класифікація функцій. Границя функції. Теореми про границі. Обчислення границь.
2
1

3.3
Перша і друга важливі границі. Наслідки.
2
1

3.4
Порівняння нескінченно малих величин, еквівалентні н.м.в. Неперервність функції, точки розриву та їх класифікація.
2
1

3.5
Похідна, її геометричний, механічний та фізичний зміст. Диференційовність та неперервність. Правила диферен-ціювання. Похідні елементарних функцій. Таблиця похідних.
2
1

3.6
Похідна складеної та оберненої функцій. Похідна функцій, заданих неявно або параметрично. Логарифмічне диференціювання.
2
1

3.7
Диференціал функції. Застосування. Похідні та диференціали вищих порядків. Формула Лейбніца
2
1

3.8
Властивості диференційовних функцій .Теореми Ролля, Лагранжа, Коші. Формули Тейлора, Маклорена. Правило Лопіталя.
2
1

3.9
Дослідження функцій. Монотонність функції. Екстремум. Інтервали опуклості та вгнутості, точки перегину.

2
2

3.10
Асимптоти. Найбільше та найменше значення функції. Загальна схема дослідження функції та побудова її графіка.
3
1

Усього за модулем №3
21
11

Усього за перший семестр

51
34
Другий семестр

Модуль №4 „ Комплексні числа. Диференціальне числення функції кількох змінних”

4.1
Комплексні числа. Основні поняття та означення. Різні форми комплексного числа. Дії над ними. Формула Ейлера. Формула Муавра. Корінь 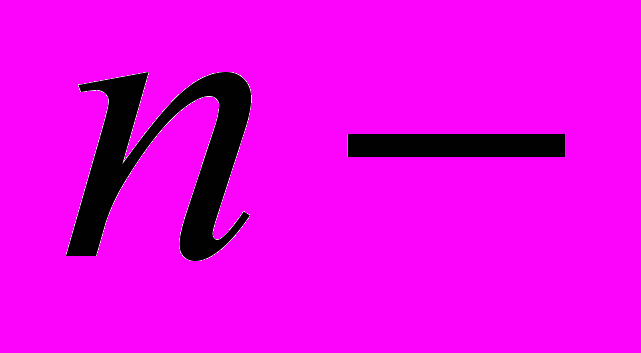го степеня з комплексного числа.

2
1

4.2
Функції кількох змінних. Основні поняття та означення. Границя. Неперервність.

2
1

4.3
Частинний і повний приріст. Частинні похідні. Диференційовність. Повний диференціал. Застосування.
2
1

4.4
Похідна складеної функції. Повна похідна. Диференціювання неявної функції. Похідні та диференціали вищих порядків. Формула Тейлора.
2
1

4.5
Дотична площина та нормаль до поверхні. Похідна за напрямом. Градієнт.
2
2

4.6
Екстремум функції двох змінних.

2
1

4.7
Умовний екстремум. Найбільше і найменше значення функції кількох змінних
2
1

Усього за модулем №4
14
8

Модуль №5 „ Інтегральне числення функції однієї змінної”

5.1
Первісна і невизначений інтеграл. Властивості. Таблиця основних інтегралів.

2
1

5.2
Основні методи інтегрування
2
1

5.3
Многочлени. Раціональні функції. Інтегрування раціональних виразів.

2
1

5.4
Інтегрування тригонометричних функцій.
2
1

5.5
Інтегрування ірраціональних функцій.
2
1

5.6
Задачі, що приводять до поняття визначеного інтеграла. Означення та властивості. Інтеграл із змінною верхнею межею. Формула Ньютона–Лейбниця.

2
1

5.7
Методи обчислення визначених інтегралів. Заміна змінної. Формула інтегрування частинами.

2
1

5.8
Невласні інтеграли з нескінченними межами інтегрування. Ознаки збіжності. Обчислення.
2
1

5.9
Невласні інтеграли від необмежених функцій. Ознаки збіжності. Обчислення.
2
1

5.10
Застосування визначених інтегралів Обчислення площ плоских фігур. Площа у прямокутних декартових координа-тах. Обчислення площі при параметричному заданні контура. Площа криволінійного сектора у полярних координатах.
2
1

5.11
Довжина дуги кривої. Об’єм тіла із заданим поперечним перерізом. Об’єм тіла обертання. Робота змінної сили. Координати центрів мас плоских областей та дуг кривих.
2
1

Усього за модулем №5
22
11

Модуль №6 „ Диференціальні рівняння”

6.1
Диференціальні рівняння першого порядку. Основні поняття та означення. Задача Коші. ДР з відокремлюваними змінними, однорідні.
2
2

6.2
Лінійні ДР, рівняння Бернуллі, у повних диференціалах.
2
2

6.3
Диференціальні рівняння вищих порядків. Основні поняття . Задача Коші. Диференціальні рівняння, які допускають зниження порядку.

2
1

6.4
Лінійні диференціальні рівняння. Поняття лінійно незалежної системи функцій. Визначник Вронського. Лінійні однорідні та неоднорідні ДР. Структура загального розв’язку.

2
1

6.5
Теорія лінійних однорідних ДР другого та вищих порядків зі сталими коефіцієнтами.
2
1

6.6
Лінійні неоднорідні ДР зі сталими коефіцієнтами і правою частиною спеціального вигляду.
2
1

6.7
Лінійні неоднорідні ДР зі сталими коефіцієнтами і правою частиною спеціального вигляду (продовження).

Метод Лагранжа (варіації довільних сталих) для лінійних ДР другого порядку.
2
2

6.8
Системи ДР. Метод виключення та інтегровних комбінацій розв’язання систем диференціальних рівнянь у нормальній формі.

2
1

6.9
Системи диференціальних рівнянь зі сталими коефіцієнтами.
2
2

Усього за модулем №6
18
13

Усього за другий семестр

54
32

Третій семестр

Модуль №7 „ Ряди”

7.1
Числові ряди. Основні поняття та означення , збіжність. Властивості ЧР. Достатні ознаки збіжності знакододатних рядів ( порівняння).
2
1

7.2
Достатні ознаки збіжності знакододатних рядів ( порівняння, Д’Аламбера, Коші).
2
1

7.3
Альтерновні ряди. Теорема Лейбниця. Знакозмінні ряди. Абсолютна і умовна збіжності.
2
1

7.4
Функціональні ряди. Основні поняття та означення. Рівномірна збіжність. Ознака Вейєрштрасса. Властивості рівномірно збіжних рядів. Степеневі ряди. Теорема Абеля. Інтервал та радіус збіжності степеневого ряду.
2
2

7.5
Властивості степеневих рядів. Ряди Тейлора та Маклорена. Застосування.
2
1

7.6
Ряди Фур’є. Гармонічні коливання. Тригонометричний ряд Фур’є. Коефіцієнти Фур’є. Достатня умова подання функції через її ряд Фур’є . Ряд Фур’є для 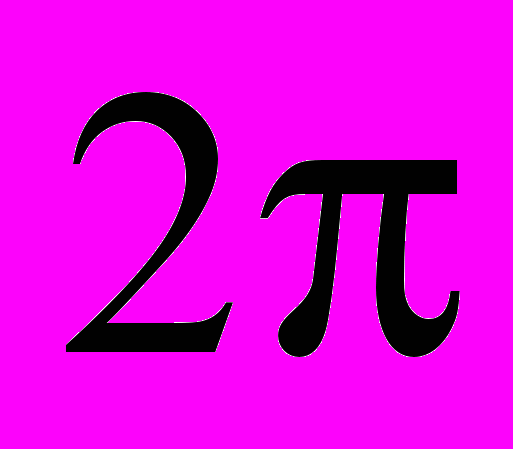періодичних функцій.
2
2

7.7
Ряд Фур’є для парних і непарних функцій. Ряд Фур’є для 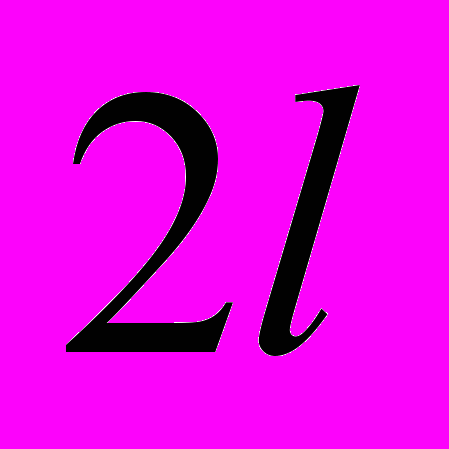– періодичних функцій.
2
1

7.8
Інтеграл Фур’є. Інтеграл Фур’є для парних і непарних функ-цій. Інтеграл Фур’є в комплексній формі.Перетворення Фур’є.
2
1

Усього за модулем №7
16
10

Модуль №8 „ Кратні, криволінійні та поверхневі інтеграли. Елементи теорії поля”

8.1
Подвійні інтеграли. Основні поняття та означення. Умови існування та властивості. Обчислення.

2
2

8.2
Заміна змінних у подвійному інтегралі. Застосування.
2
1

8.3
Потрійні інтеграли. Основні поняття та означення. Обчислення. Системи координат у просторі. Заміна змінних у потрійному інтегралі. Застосування.
2
2

8.4
Криволінійні інтеграли першого та другого роду. Властивості та обчислення.
2
1

8.5
Формула Гріна. Умови незалежності криволінійного інтеграла від форми шляху інтегрування. Інтегрування повних диференціалів
2
2

8.6
Поверхневі інтеграли першого роду. Властивості та обчислення.

2
1

8.7
Поверхневі інтеграли другого роду. Властивості та обчислен-ня. Формула Остроградського–Гаусса. Формула Стокса.
2
2

8.8
Елементи теорії поля. Скалярні та векторні поля. Векторні лінії. Градієнт скалярного поля. Похідна за напрямом.

2
1

8.9
Потік, циркуляція, дивергенція, ротор векторного поля.
2
2

8.10
Оператор Гамільтона. Безвихрове, потенціальне, соленоїдне поля. Диференціальні операції першого та другого порядків.
2
1

Усього за модулем №8
20
15

Модуль №9 „ Теорія функції комплексної змінної”

9.1
Комплексні числа. Функція комплексної змінної, границя, неперервність. Основні елементарні функції.
2
1

9.2
Диференціювання функції комплексної змінної . Аналітичні функції. Умови Коші–Рімана. Гармонічні функції. Геометричний зміст модуля і аргумента похідної
2
1

9.3
Інтегрування функції комплексної змінної. Інтегральна теорема та формула Коші.
2
2

9.4
Ряди в комплексній області
2
1

9.5
Ряди з комплексними членами. Ряди Тейлора і Лорана.
2
1

9.6
Нулі функції. Ізольовані особливі точки, їхня класифікація.
2
1

9.7
Елементи теорії лишків. Застосування до обчислення інтегралів.
2
2

9.8
Елементи теорії лишків. Застосування до обчислення інтегралів.
1
1

Усього за модулем №9
15
10

Усього за третій семестр

51
35

Четвертий семестр

Модуль №10 „ Операційне числення”

10.1
Оригінал та зображення за Лапласом, їхні властивості , знаходження. Теореми єдиності та лінійності. Теореми зсуву, запізнення, випередження.
2
1

10.2
Диференціювання та інтегрування оригіналу і зображення. Зображення періодичного сигналу.

2
2

10.3
Зображення ступінчатих функцій. Зображення згортки функцій. Формула Дюамеля.
2
2

10.4
Знаходження оригіналу дробово–раціональної функції. Елементарні засоби знаходження оригіналів. Перша та друга теореми розкладання
2
1

10.5
Застосування перетворення Лапласа до розв’язування диференціальних рівнянь.

2
1

10.6
Інтеграл Дюамеля. Розв’язання систем лінійних диференціальних рівнянь
2
1

Усього за модулем №10
12
8

Модуль №11 „ Чисельні методи”

11.1
Наближене розв’зування рівнянь. Метод спроб (половинного поділу або дихотомії). Методи хорд.

2
1

11.2
Метод дотичних (Ньютона). Комбінований метод. Точність і збіжність методів.
2
1

11.3
Наближене обчислення визначеного інтеграла. Квадратурні формули прямокутників, трапецій, Сімпсона.

Абсолютні похибки квадратурних формул.
2
1

11.4
Інтерполювання функцій. Інтерполяційний многочлен Лагранжа. Похибка інтерполяційної формули. Інтерполяційна формула Лагранжа для рівновіддалених вузлів.
2
2

11.5
Інтерполювання сплайнами. Визначення сплайн-функції. Найпростіша задача наближення лінійними сплайнами.  Алгоритм побудови кубічної сплайн-функції.

2
2

11.6
Принципи побудови методу найменших квадратів. Оцінка якості апроксимації методом найменших квадратів.
2
1

11.7
Наближене розв’зування ДР методами Ейлера та Рунге-Кутта.

2
1

Усього за модулем №11
14
9

Модуль №12 „ Теорія ймовірностей та елементи математичної статистики”

12.1
Випробування і події. Класичне, геометричне та статистичне означення ймовірності. Елементи комбінаторики. Обчислення ймовірностей.
2
1

12.2
Умовна ймовірність.Теореми про ймовірність суми та добутку подій.

2
1

12.3
Формула повної ймовірності. Формула Байєса.
2
1

12.4
Випробування Бернуллі. Теореми Муавра-Лапласа. Формула Пуассона.
2
1

12.5
Дискретні та неперервні випадкові величини. Ряд розподілу. Інтегральна функція та щільність ймовірності.
2
1

12.6
Математичне сподівання, дисперсія, їх властивості та ймовірнісне тлумачення. Мода і медіана. Моменти.
2
1

12.7
Біноміальний, геометричний, гіпергеометричний закони розподілу, їх характеристики. Рівномірний, нормальний, показниковий закони розподілу, їх характеристики.
2
1

12.8
Закон великих чисел. Нерівність Чебишова. Теореми Чебишова та Бернуллі.
2
1

12.9
Двовимірні випадкові величини. Закони розподілу двови-мірних величин. Інтегральна функція та щільність розподілу.

Математичне сподівання та дисперсія.
2
1

12.10
Залежність випадкових величин. Умовні закони розподілу. Кореляційний момент і коефіцієнт кореляції випадкових величин.
2
1

12.11
Випадкові функції. Стаціонарні випадкові функції. Спектральний розклад. Ергодична властивість стаціонарних випадкових функцій. Стандартні випадкові процеси.
2
1

12.12
Предмет математичної статистики. Генеральна та вибіркова сукупності. Вибірковий метод. Полігон та гістограма. Емпірична функція. Числові характеристики статистичного розподілу.
2
1

12.13
Оцінки невідомих параметрів. Поняття оцінки параметрів. Властивості статистичних оцінок. Точкові та інтервальні оцінки. Властивості оцінок. Побудова довірчих інтервалів.
2
2

12.14
Статистичні гіпотези, похибки, критерії перевірки статистичних гіпотез.
2
1

Усього за модулем №12
28
15

Усього за четвертий семестр

54
32

Усього за навчальною дисципліною
210
133


2.2.3. Індивідуальна робота