Диссертация на соискание ученой степени

Вид материала

Диссертация

Содержание 3.4Двухотраслевая модель с учетом сектора НИОКР 3.4.2Поведение модели

Подобный материал:

• Диссертация на соискание ученой степени, 3188.43kb.
• Диссертация на соискание учёной степени кандидата юридических наук, 1614.07kb.
• М. С. Тарков Математические модели и методы отображения задач обработки изображений, 17.1kb.
• Диссертация на соискание ученой степени кандидата экономических наук, 2079.82kb.
• Диссертация на соискание ученой степени доктора психологических наук, 5248.42kb.
• Диссертация в форме научного доклада на соискание ученой степени доктора медицинских, 907.5kb.
• Диссертация на соискание ученой степени, 3924.03kb.
• Диссертация на соискание ученой степени, 2781.79kb.
• Диссертация на соискание ученой степени, 2577.32kb.
• Диссертация на соискание ученой степени, 2127.42kb.

3.4Двухотраслевая модель с учетом сектора НИОКР

3.4.1Предпосылки и формальное описание модели

В двухотраслевой экономике, описанной в разделах 3.1 и 3.2, предполагается, что внутри экономики всегда существует достаточное предложение интеллектоемких ресурсов для добывающих и обрабатывающих отраслей. Однако зачастую в реальной экономике получение необходимой технологии или квалифицированных кадров представляет достаточно сложную задачу, и экономические агенты для ее решения вынуждены выходить на мировой рынок интеллектуальных ресурсов. Аналогично, зачастую по тем или иным причинам местные интеллектуальные ресурсы оказываются неконкурентоспособными на мировых рынках и потому непригодными к экспортированию, что приводит к дисбалансу спроса и предложения в индустрии производства интеллектуального капитала. Например, в начале 1990-х гг. российские научно-исследовательские институты имели завышенные ожидания относительно конкурентоспособности их конструкторских разработок и технологий на мировых рынках и даже в отечественной индустрии; предъявленный же спрос оказался значительно ниже ожиданий (так, в 2001 г. платежи за использование интеллектуальной собственности в РФ составили только 0,4 долл./чел. против 135,5 долл./чел. в США; высокотехнологичный экспорт РФ составил только 8% экспорта промышленных товаров или 0,6% ВВП, против 32% в США, или 2,9% ВВП [UNDP, 2003]) и вкупе с рядом других факторов привел к массовому «вымыванию» квалифицированного персонала из данной сферы

В модифицированной двухотраслевой модели можно предположить наличие выделенного сектора НИОКР³², производящего интеллектоемкие ресурсы – осуществляющего обучение (высшее и среднее специальное) рабочей силы и разрабатывающего различные технологии производства. Спрос на продукцию данного сектора предъявляют отрасли, инвестирующие в интеллектоемкий капитал. Кроме того, можно предположить, что существует возможность (ограниченная или неограниченная) покупать и продавать технологии и другие формы интеллектуального капитала на мировом рынке. Основной производительной силой в данном секторе также будет являться интеллектуальный капитал. Содержательные схемы модифицированной двухотраслевой модели представлены ниже (Рисунок 8 и Рисунок 9).

Объем производства (предложение) данного сектора будет зависеть от задействованных в нем интеллектуального капитала и рабочей силы:

S₃ = VA₃ = ₃LM₃^3 (9.1)

что является модификацией уравнения (2.1) при предположении ₃=0.

Динамика ресурса M₃ описывается аналогично уравнениям (2.5)-(2.7).

Таким образом, предлагаемая модель является модификацией подхода П. Ромера к сектору НИОКР [Romer, 1990] (см. также раздел 2.3.3); однако делается предположение о снижающейся производительности труда в данном секторе (0<₃<1), поскольку гипотеза Ромера о возрастающей продуктивности данного сектора на текущий момент не нашла эмпирического подтверждения (более того, эмпирические данные показывают, что при сохранении уровня расходов крупнейших стран-исследователей на НИОКР, темпы роста в этих странах стали снижаться).

Внутренний спрос со стороны отраслей на интеллектуальный капитал будет определяться

D₃ = I_Mi (9.2)

При этом, можно предположить, что спрос со стороны самого сектора НИОКР пропорционален спросу на интеллектуальный капитал со стороны других отраслей:

I_M3 =  (I_M1 + I_M2) (9.3)

Если предположить, что существует свободный рынок интеллектуального капитала, то любой излишек произведенных технологий может быть экспортирован, а любой дефицит технологий может быть «закрыт» с помощью их импорта. Тогда

S₃ > D₃: Ex₃ = S₃ - D₃ (9.4.1)

S₃ < D₃: Im₃ = D₃ - S₃ (9.4.2)

Однако иная ситуация возникает в случае, если не существует свободного рынка интеллектуального капитала. Данное предположение представляется более разумным в силу того, что рынок технологий очень ограничен (и имеет в мире тенденцию к сокращению), а основная часть технологии поставляется в страны в виде прямых иностранных инвестиций (см. [Mani, 2002], PP. 19-21).

Тогда, в случае, когда есть избыточная потребность в интеллектуальных ресурсах, эта потребность может быть компенсирована со стороны мирового рынка (уравнение (9.4.2)). Однако в случае, если существует излишек предложения технологий, этот излишек не может быть экспортирован. Таким образом, отрасли будет компенсирован только тот объем технологий и других интеллектуальных ресурсов, который найдет потребление внутри данной страны; соответственно, это приведет к сокращению национального дохода за счет добавленной стоимости сектора НИОКР (в доходной части) и за счет сокращения конечного потребления (в расходной части):

S₃ > D₃, Ex₃ = 0 => VA’₃ = VA₃ – (S₃ - D₃) (9.5.1)

C’ = С – (VA₃ – VA’₃) (9.5.2)


Р
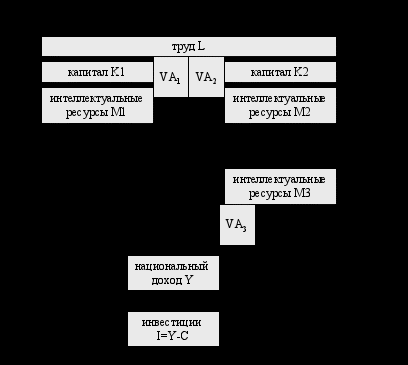
исунок 8. Воспроизводство ресурсов в двухотраслевой модели с учетом сектора НИОКР


Рисунок 9.
Структура потоков в двухотраслевой модели с учетом сектора НИОКР

3.4.2Поведение модели

Сходимость модели

Рассмотренный в разделе 3.3.3 анализ сходимости модели учитывал динамику четырех основных переменных (K₁, M₁, K₂, M₂) и демонстрировал сходимость системы к равновесной точке (K₁*, M₁*, K₂*, M₂*). Однако логика приведенного доказательства будет справедлива и для большего количества отраслей, в том случае, если производство в этих отраслях следует уравнению (2.1) и (2.3) (частный случай для отрасли производства интеллектоемких ресурсов (9.1)), а инвестиции – уравнению (2.7). Таким образом, можно показать, что для рассматриваемой в данном разделе модели с сектором производства интеллектуальных ресурсов, в том случае, если ограничения отсутствуют, модель из любого начального состояния (K₁, M₁, K₂, M₂, M₃) будет сходиться к равновесному состоянию (K₁*, M₁*, K₂*, M₂*, M₃*).

В том случае, если учитываются ограничения (9.5.1)-(9.5.2), введенные выше, модель может демонстрировать три типа динамики, аналогичные рассмотренным выше в разделе 3.3.3 (подраздел «Роль ограничений»): (а) ограничения не влияют на сходимость, (б) ограничения замедляют сходимость, (в) система не сходится к равновесному состоянию случая без ограничений. Однако, в отличие от ситуации в разделе 3.3.3, наиболее распространенным следует считать варианты (а) и (в).

Особенности поведения в случае наличия ограничений зависят от ряда факторов. В частности, запас интеллектуальных ресурсов в секторе НИОКР является избыточным, т.е. превышает потребности отраслей, то система конвергирует к траектории роста с учетом ограничений, а весь избыточный потенциал амортизируется и исчезает (скорость конвергенции будет зависеть от параметра _M3).

Максимизация

Задача максимизации для трех отраслей без наличия ограничений и при условии постоянных инвестиционных пропорций разрешается аналогично решению в разделе 3.3.4, т.е. существует оптимизирующее решение (₃^*=0, т.к. в секторе используется только интеллектуальный капитал)

s₁^*, s₂^*, s₃^* = argmax Y^*(₁^*,₂^*) (9.6.1)

₁^*, ₂^* = argmax Y^* (s₁, s₂, s₃) (9.6.2)

где s₁^*, s₂^*, s₃^* >0. Формальное решение максимизационной задачи здесь не приводится.