Geum.ru

Диссертация на соискание ученой степени

Вид материалаДиссертация
3.3Исследование двухотраслевой модели
Таблица 7. Основные сценарии экономической динамики в двухотраслевой экономике
3.3.2 Основные результаты моделирования: сбалансированный рост
3.3.3Сходимость при стационарных пропорциях инвестиций
3.3.4Оптимизация при стационарных пропорциях инвестиций
Подобный материал:
1   ...   7   8   9   10   11   12   13   14   ...   18

3.3Исследование двухотраслевой модели

3.3.1Сценарии экономической динамики


На дискретной версии модели, представленной выше (при предположении о переменной норме инвестиций в отрасли), был реализован ряд имитационных экспериментов [Luksha, 2003]. Эти эксперименты позволили определить ключевые сценарии экономического развития в двухотраслевой модели (пример этих имитационных экспериментов дан ниже, Рисунок 6). Сценарии обобщаются в приводимой ниже таблице (Таблица 7). Каждый из приведенных сценариев можно наблюдать в реальной переходной экономике.

Таблица 7. Основные сценарии экономической динамики в двухотраслевой экономике

№ п/п
Описание
Формальное описание
Примеры

I
«баланс» ресурсных и обрабатывающих отраслей (некоторый минимальный объем экспорта, в основном продукции ресурсных отраслей)
Q1 = Q1D

Q2 = Q2D
экономика Советского Союза

II
Спад производства в обрабатывающей отрасли; дефицит на рынке конечного товара компенсируется импортом, избыточный промежуточный товар экспортируется
Q1 > Q1D || Ex1>0

Q2 < Q2D || Im2>0
Россия, Украина

III
Практически полное исчезновение обрабатывающего сектора; выручка от экспорта продукции добывающего сектора используется для приобретения импортной конечной продукции
Q1>Q1D=0 || Ex1=Q1

Q2 =0 || Im2=Q2D
Казахстан, Туркменистан

IV
Развитие обрабатывающего сектора; добывающая промышленность снабжает в основном отечественную обрабатывающую промышленность
Q1 < Q1D || Im1>0

Q2 > Q2D || Ex2>0
страны Восточной Европы

V
Практически полное исчезновение сырьевого сектора; выручка от экспорта продукции обрабатывающего сектора используется в т.ч. для приобретения импортного сырья
Q1 =0 || Im1=Q1D

Q2 >Q2D ||
Ex2= Q2 - Q2D
(не среди переходных экономик): напр. Италия



Сценарии представлены на схеме, приведенной ниже (Рисунок 6) Серыми стрелками обозначены потенциальные переключение между сценариями. Сценарий I является особенно нестабильным, поскольку постоянный баланс двух отраслей в экономике может быть достигнуто только через контроль цен, регулирование спроса/предложения, а также контроль экспорта/импорта. Когда происходит либерализация экономики, эти ограничения снимаются, и система эволюционирует либо к сценарию II (сокращение обрабатывающей отрасли), либо к сценарию IV (рост обрабатывающей отрасли). Сценарий II может также эволюционировать к сценарию III (полное исчезновение обрабатывающей промышленности); аналогично, сценарий IV может эволюционировать к сценарию V (когда сырье для отраслей закупается практически полностью за рубежом, что можно наблюдать в случае развитых европейских стран). В своем развитии, как правило, экономика может переключаться между сценарием II (добывающий сектор растет быстрее) и сценарием IV (быстрее растет обрабатывающий сектор) в зависимости от внешних и внутренних условий.

Исходное состояние российской экономики как части экономики СССР до перехода представляло собой сбалансированную систему ресурсных и обрабатывающих отраслей (существовал определенный объем экспорта, в основном продукции ресурсных отраслей). Такое состояние сопровождалась производством неудовлетворительного (с потребительской точки зрения) набора для рынка конечной продукции.

Очевидно, что состояние «сбалансированности» ресурсных и обрабатывающих отраслей может существовать только в плановой экономике, изолированной от внешнего рынка. В рыночных экономиках следует ожидать ситуаций либо более активного развития ресурсных отраслей (и тогда значимая часть сырья, не находя спроса на внутреннем рынке, уходит на экспорт), либо активного развития обрабатывающих отраслей (и тогда страна нуждается в больших объемах сырья, чем способна производить сама)

Элементом программы либерализации экономики в 1990-х явилась либерализация внешнеэкономической деятельности. В результате, рынок готовой продукции был в значительной мере занят импортными продуктами. Как следствие, произошло сокращение внутреннего спроса на сырье, и потоки продукции сырьевых отраслей в значительной мере переориентировались на работу на экспорт. Дефицит ресурсов в экономике – снижение уровня жизни (уровня потребления) у населения в среднем, а также снижение совокупного объема инвестиций

Вариант прогнозного развития (дальнейшее развитие по пути сценария II): постепенное окончательное разрушение обрабатывающей промышленности; создание добавленной стоимости только в ресурсной промышленности, когда доходы от экспорта направляются на потребление и воспроизводство основного капитала

Вариант прогнозного развития: развитие обрабатывающей промышленности, постепенно переключающее сырьевые отрасли с внешнего на внутренний рынок. В какой-то момент времени потребности обрабатывающей отрасли могут превысить объемы производства ресурсной отрасли, и страна из чистого экспортера сырья может стать чистым импортером. Избыточный продукт обрабатывающих отраслей, при его достаточной конкурентоспособности, может экспортироваться.

Такой сценарий был реализован в ряде стран ЦВЕ, например, в Чехии и в Польше. Однако эти страны традиционно развивали свою обрабатывающую промышленность (поскольку их природные ресурсы находятся в достаточно истощенном состоянии), и их история закономерно ведет их по этому пути (напр. индустриализация в этих странах произошла на полвека раньше, чем в республиках СССР [Камерон, 2000]) Описание процессов перехода для стран Восточной Европы и влиявших на них факторов предлагается в исследовании Свейнара [Svejnar, 2002a]).


Рисунок 6. Некоторые варианты моделирования динамики двухотраслевой модели

Пример моделирования динамики без учета ограничений

1=0.2, 1=0.7, 2=0.7, 2=0.2, s1=0.3, s2=0.1, 2=1.2, 1=2=1=1


национальный доход Y пропорции добавленной стоимости

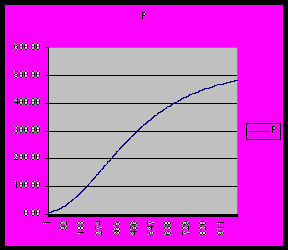
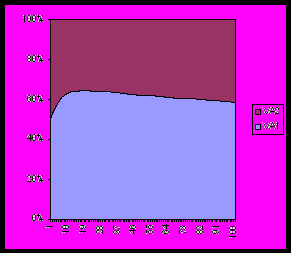по отраслям


структура предложения на структура предложения на

рынке сырья рынке готовой продукции




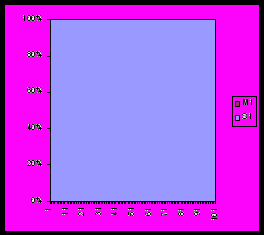
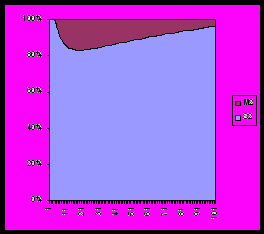
(спрос удовлетворяется внутренней (спрос удовлетворяется внутренней

отраслью) отраслью и импортом, доля

последнего сокращается)


Р
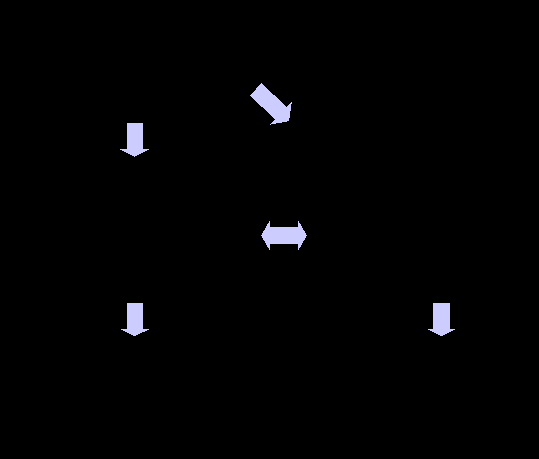
исунок 7. Сценарии развития экономики в двухотраслевой модели


3.3.2 Основные результаты моделирования: сбалансированный рост


В предложенной двухотраслевой модели стоит задача определения оптимального сценария развития и условий его достижения. Как и всегда в подобных моделях, источником долгосрочного роста являются инвестиции в факторы производства, т.е. необходимо определить оптимальную пропорцию распределения инвестиционных ресурсов между секторами экономики и внутри секторов между производственными ресурсами.

Для итогового результата очень важно сформулировать корректные критерии оптимальности сценария.

Например, в экономической практике часто ставится задача достижения максимально быстрых темпов роста в краткосрочной перспективе. Однако задача максимизации темпа экономического роста в текущем периоде Yt/Yt, (в случае, если определена предельная норма инвестиций s: s1+s2=s)):

s1, s2 = argmax Y (6.1)




(6.2)

ведет к «инвестиционной близорукости», когда все средства инвестируются в более производительную отрасль (s1=s, s2=0 если выражение в скобках больше для первого члена уравнения; s1=0, s2=s, если выражение в скобках больше для второго члена уравнения). Как следствие, падает выпуск в недоинвестированной отрасли (которая, как следствие, становится еще менее производительной);конечным результатом при такой политике будет полное исчезновение менее производительной отрасли, и, как следствие, общее падение производительности (и иногда схлопывание) более производительной отрасли. Поддержание постоянных пропорций инвестирования является более предпочтительным для экономики, чтобы достичь более высокого уровня национального дохода в долгосрочной перспективе, хотя в краткосрочной перспективе экономика может иметь более низкие темпы роста.

Для базового случая (без учета ограничений в модели), при предположении о фиксированных пропорциях инвестиций между отраслями и факторами, модель сходится к равновесному состоянию в том случае, если

ii, ii <1 (6.3)

Доказательство сходимости для простейшего случая (Ki = Mi = 1, i=1, i=1) приведено в разделе 3.3.3. Аналогичные результаты о сходимости двухсекторной неоклассической модели в предположении о фиксированном распределении инвестиций были получены Инадой [Inada, 1963].

В противном случае модель демонстрирует взрывную динамику (постоянно ускоряющийся рост). Это одна из возможностей отобразить напр. растущую сравнительную компенсацию за интеллектуальные ресурсы (или возрастающую полезность интеллектуальных ресурсов, введенную Ромером [Romer, 1989]).

В равновесном состоянии (для случая Ki=Mi=1, i=1, i=1):

Y*=Y*(1, 2, 1, 2, 1, 2, 1, 2, s1, s2, K1, K2, M1, M2, L) (6.4)

Тогда существует оптимальная пропорция распределения инвестиционных ресурсов между отраслями и внутри отраслей, максимизирующая выпуск в стационарном состоянии, если определена предельная норма инвестиций s:

s1*, s2* = argmax Y*(1*,2*) (6.5.1)

1*, 2* = argmax Y* (s1, s2) (6.5.2)

Формальное решение данной задачи приведено в разделе 3.3.4.

Таким образом, основные выводы представленной модели заключаются в следующем.

Во-первых, целевая задача максимизации темпов экономического роста может приводить к экономическим решениям, не являющимся эффективными в долгосрочной перспективе. Для экономических планировщиков целесообразно ставить задачи, обеспечивающие высокий уровень роста национального дохода на больших временных промежутках31.

Во-вторых, существует оптимальный способ распределения инвестиций между отраслями и факторами производства, обеспечивающий максимальный уровень ВВП в долгосрочной перспективе. Этот уровень достигается за счет сбалансированного роста экономики, предполагающего инвестиционное финансирование в определенных пропорциях.

Эмпирическая верификация полученных результатов на временных рядах экономики РФ затруднена по следующим причинам:
  • в течение первого десятилетия реформ (1990-1998 гг.) трансформационные процессы (изменение структурных пропорций и формирование институциональной инфраструктуры) оказывали большее влияние на динамику основных макропоказателей экономики, чем нормальные процессы экономического воспроизводства;
  • после внешнего шока, вызванного девальвацией рубля, рост в 1999-2000 гг. носил скорее регенерационный характер (т.е. восстанавливались уже существующие в экономике мощности, а не работал нормальный цикл развития капиталистической экономики «инвестиции-рост»)
  • рост за счет инвестиций в основные фонды начался в России только в 2001-
    2002 гг.; таким образом, временной ряд для анализа процессов роста недостаточен для каких-либо статистически значимых выводов.

Кроме того, эмпирическое тестирование модели на массивах данных переходных экономик затруднено невозможностью непосредственного измерения запаса интеллектуальных ресурсов. В аналогичной ситуации для оценки моделей роста с учетом человеческого капитала косвенным индикатором служит уровень образования населения (доля населения со средним образованием, доля населения с высшим образованием), оценка проводится на больших промежутках времени (десятилетия). Кроме того, на настоящий момент не существует индикаторов, позволяющих измерять конкурентоспособность интеллектуальных ресурсов (научных разработок и технологий) с т.з. создания ими добавленной стоимости на уровне экономики в целом. Таким образом, выводы предложенной модели носят скорее содержательный характер.

3.3.3Сходимость при стационарных пропорциях инвестиций


Необходимо доказать, что при любых значениях параметров и начальных данных система, описанная уравнениями, сходится к стационарной точке. Обозначим ее через
(X1*, X2*, X3*, X4*).

Сначала докажем сходимость к стационарной точке при следующих начальных условиях:

(7.1)

где d - некоторая константа. Пусть d>1, тогда для любого k,

(7.2)

Для состояния в момент времени t=1:


(7.3)

где

(7.4)

Таким образом,

(7.5)

Для произвольного момента времени k:

(7.6)

При d>1, последовательность {ak}, a0=d, ak+1=f(ak) монотонно сходится к 1, то есть Xik стремится к Xi*. Аналогичным образом доказывается сходимость при d<1.

Для произвольного начального условия

существуют константы D>1>d>0 такие, что

(7.7)

Обозначим за Uik значения на k-м шаге для последовательности, начинающейся в D*Xi*, а за Dik значения на k-м шаге для последовательности, начинающейся в d*Xi*. Обе эти последовательности сходятся к Xi*.

Так как

(7.8)

то

(7.9)

а значит, Xik и сходится к Xi*.

Существование равновесного состояния модели, к которому она эволюционирует из любого начального состояния, показывает, что в случае, если бы все страны придерживались стратегии поддержания постоянного уровня накоплений в отраслях, то в долгосрочной перспективе стоило бы ожидать установления «глобального равновесия» национальных страновых доходов. При этом, как видно из уравнения (8.11) ниже, точка равновесия для каждой страны будет зависеть от количества занятых в экономике страны и параметров производительности физического и интеллектоемкого капитала в отраслях.

Таким образом, модель двухотраслевой экономики с данным набором исходных свойств имеет равновесие типа «устойчивый узел»; подобный результат можно считать развитием работы Манкива и др. [Mankiw et al., 1992], показавших наличие устойчивого равновесного состояния для системы с накоплением интеллектуальных ресурсов, но без учета внутренней отраслевой структуры.

Роль ограничений

В случае наличия ограничений вида (4.1)-(4.7), введенных в разделе 3.2.3, имитационным экспериментом идентифицированы три основных типа их влияния на динамику модели:

а. ограничения не влияют на процесс сходимости модели (нет воздействия);

б. ограничения замедляют процесс сходимости (слабое воздействие);

в. система не сходится к равновесному состоянию случая без ограничений, напр. коллапсирует к нулю (критическое воздействие).

При условии постоянных инвестиционных пропорций (5.1.1)-(5.1.2) наиболее регулярно реализуется вариант динамики (б); таким образом, ограничения не оказывают принципиального воздействия на решение в равновесном состоянии. Вариант
динамики (в) реализуется при некотором достаточно ограниченном наборе параметров и начальных условий; специальное исследование обстоятельств, приводящих к данному типу динамики, не входило в задачу данного исследования.

3.3.4Оптимизация при стационарных пропорциях инвестиций


Критерием, определяющим оптимальность сценария при константных нормах сбережения в отраслях, может служить задача максимизации долгосрочного (равновесного) уровня национального потребления.

Соответственно, стоит задача определения нормы сбережения и параметров распределения инвестиций, максимизирующих национальное потребление C=(1-s)Y через максимизацию национального дохода Y при условии равенства суммы констант производственной функции (2.2) и при условии стационарности норм сбережения в отраслях (5.1.1)-(5.1.2).

Сначала попробуем найти параметры, максимизирующие национальный доход Y при заданной норме сбережений.

Рассмотрим динамику системы в дискретном времени. Имеем следующие зависимости

(8.1)


При t система сходится к решению (K1, M1, K2, M2). Доказательство сходимости представлено выше (раздел 3.3.3).

Для этого решения можно записать следующие уравнения



(8.2)


Из них можно выразить



(8.3)


и
подставить полученные значения в выражение для национального дохода Y

(8.4)

Пусть

 = 1 + 1 = 2 + 2 (8.5)

тогда



(8.6)


Значения 1, 2, максимизирующие национальный доход, имеют следующий вид



(8.7)


После подстановки получим:



(8.8)


Далее, поскольку s1 + s2 = s, то Y принимает максимальное значение при



(8.9.1)


где



(8.9.2)


Таким образом, указанные значения параметров s1, s2, обеспечивают максимальный национальный доход в стационарном режиме при заданном значении s.

Пусть



(8.10)


Тогда, при заданном значении s максимальное значение национального дохода Y имеет следующий вид




(8.11)


где E – очевидным образом вычисляемая константа, зависящая от параметров рассматриваемой экономики. Максимальное значение потребления при заданной норме сбережений имеет следующий вид

(8.12)


Максимум выражения (8.12) достигается при

s =  (8.13)

Таким образом, при заданных условиях и параметрах модели максимальное значение потребления достигается, когда ограничение нормы сбережений равно . При этом, распределение инвестиций между отраслями определяется по формуле (8.9.1)-(8.9.2), а распределение инвестиций внутри отрасли определяется по формуле (8.7).

Таким образом, при условии стратегии постоянного поддержания инвестиционных пропорций (условие (5.1.1)-(5.1.2)) и при выполнении предпосылки о снижающейся отдаче инвестиций в интеллектуальный капитал максимальный доход на одного работающего будет ограничен выражением (8.11) при условии (8.13)

Данный результат представляет собой аналог «золотого правила накопления» Солоу для случая двухотраслевой модели (добывающий и обрабатывающий сектора) с учетом интеллектоемкости производства.