Geum.ru

Диссертация на соискание ученой степени

Вид материалаДиссертация
3.2Базовая двухотраслевая модель
L – объем труда (предполагается константой) i
3.2.2Спрос и предложение в двухотраслевой модели
3.2.3Введение ограничений
3.2.4Динамика объемов инвестиций
Подобный материал:
1   ...   6   7   8   9   10   11   12   13   ...   18

3.2Базовая двухотраслевая модель

3.2.1Производство и распределение национального богатства


Приведенные в данном разделе уравнения позволяют описать динамику производства и инвестиций в системе, состоящей из произвольного числа отраслей.

Добавленная стоимость VAi, производимая в i-й отрасли, может быть представлена как

(2.1)

где

L – объем труда (предполагается константой30)

i – доля труда, направляемая в i-ю отрасль (1i0, i =1),

Ki – запас физического капитала в i-й отрасли,

Mi – запас интеллектуальных ресурсов в i-й отрасли,

i, i – константы в производственной функции (1i0, 1i0, i+i1).

В данной модели не является целью рассмотрение эмпирически известного факта о растущей компенсации за интеллектуальные ресурсы; однако возможно ввести ее в модель в том случае, если i1.

Также предполагается, что

i+i=j+j  i, j (2.2)

В противном случае предельная производительность инвестиций в одну отрасль всегда будет превышать производительность инвестиций в другую отрасль, и не может возникать вопрос о целесообразности некоторого «распределения» инвестиций между отраслями (наиболее целесообразным будет являться инвестирование в наиболее производительную отрасль).

Национальный доход Y представляет собой сумму добавленных стоимостей отраслей:

(2.3)


Распределение национального дохода достаточно традиционно представляется как

Y=C+I+S’ (2.4)

где

C – национальное потребление,

I – национальные инвестиции,

S’ - ‘мертвый груз’ сбережений (такое явление может наблюдаться напр. в экономиках с плохо функционирующей банковской системой, где население предпочитает хранить деньги напр. в виде иностранной валюты у себя дома, либо иным образом извлекать часть полезного продукта из экономики; в эффективно функционирующей рыночной экономике S’=0).

Хотелось бы отметить, что для экономики РФ показатель «мертвого груза сбережений» один из самых высоких в мире (норма национальных сбережений составляет около 30%, а норма валовых накоплений около 20%, т.е. расхождение около 10%) [Белоусов, 2003], что свидетельствует в пользу необходимости серьезной реформы финансового сектора. В работе соискателя данный аспект не рассматривается в силу объективных сложностей его моделирования; он не оказывает принципиального влияния на выводы модели, поскольку используется параметр «склонности к инвестированию», характеризующий долю ВВП, направляемую на валовые накопления. Однако следует заметить, что для достижения оптимального уровня инвестиций необходима мобилизация и «мертвого груза», что следует учитывать при разработке политики стимулирования роста.

В данной работе отдельно не рассматриваются вопросы налогового поведения государства, в т.ч. вопрос оптимального уровня налогообложения реального сектора, ранее рассмотренный соискателем [Лукша, 2000b].

Инвестиции распределяются между основными факторами производства M и К:

(2.5.1)


Это выражение может также быть представлено как

(2.5.2)

где

si – доля национального дохода, инвестируемая в i-ю отрасль (1si0, sis<1),

s – некоторая константа, ограничивающая норму инвестиций в экономике, s=I/Y.

i – доля инвестиций в i-й отрасли, которая инвестируется в физический капитал
Ki (1i0).

Коэффициенты si, i могут быть постоянными или варьирующимися во времени. Вопрос о динамике данных показателей (играющих ключевую роль для модели) рассматривается ниже, раздел 3.2.4.

Динамика запасов производственных факторов в i-й отрасли описывается как


(2.6)

где

Ki, Mi – нормы амортизации,

Ki, Mi, i, и i – некоторые константы, определяющие эффективность инвестиций в данный ресурс в данной отрасли.

В простейшем случае, Ki = Mi = 1, i=1, i=1, т.е.



(2.7)

Простейшая структура производства и инвестиций для двухотраслевой экономики представлена ниже (см. Рисунок 4)

Можно предположить, что производительность интеллектуальных ресурсов минимальная в добывающей отрасли и максимальна в обрабатывающей отрасли, т.е. 2>10. Кроме того, инвестиции в интеллектуальные ресурсы в обрабатывающей отрасли могут быть выше, чем в остальные ресурсы, 2>1 (1=2=1=1).

3.2.2Спрос и предложение в двухотраслевой модели


Структура добавленной стоимости в отраслях позволяет определить размер внутреннего предложения и объемы иностранной торговли. Можно предположить, что цена продукта добывающей отрасли P1, а цена продукта обрабатывающей индустрии P2.

Тогда добывающая отрасль производит (и предлагает) количество своего продукта Q1:



(3.1)

Можно предположить, что в обрабатывающей отрасли реализована технология леонтьевского типа, т.е. для производства одной единицы конечного продукта требуется единиц промежуточной продукции. Тогда спрос в обрабатывающей индустрии на сырье (рынок промежуточного блага) определяется как

(3.2)

где

 - коэффициент технологического использования сырья (можно предположить для простоты модели, что =1). Очевидно, что, P2>P1 (цена продукта второй отрасли превосходит стоимость сырья).

Обрабатывающая отрасль производит (и предлагает) количество продукта Q2 (случай =1):



(3.3)

Спрос на рынке конечной продукции, согласно изложенной выше логике, включает в себя конечное потребление и все виды инвестиционного потребления:



(3.4)

Размер импорта и экспорта при условии отсутствия ограничений определяется как разрыв между спросом и предложением на товарных рынках (избыточный продукт экспортируется, а дефицит продукта компенсируется импортом)




(2.5)


Элементарная структура товарных потоков в двухотраслевой модели представлена ниже (Рисунок 5).

3.2.3Введение ограничений


Модель, введенная в разделах 3.2.1-3.2.2, допускает аналитическое решение в том случае, если задан формальный критерий оптимальности (поскольку раздел 3.2.1 представляет собой вариацию традиционной неоклассической модели экономического роста, а раздел устанавливает формальное соответствие монетарных показателей модели с физическими показателями спроса и предложения условного товара в агрегированных отраслях).

Очевидно, что решение будет опираться на достаточно серьезную предпосылку о том, что свободная внешняя торговля будет способна «безболезненно» ликвидировать любые внутренние неравновесные состояния. Однако развитие на внешних рынках, как правило, ограничено высокой конкуренцией, а внутренние рынки, единожды отданные импортным товарам, достаточно сложно отобрать. Поэтому в модель может быть введен ряд ограничений, предполагающий, что реальное предложение будет ограничено либо размером производственных мощностей (определяемых запасами производственных факторов), либо рыночным спросом (который редко может расти быстрее, чем с определенным темпом, напр. рост мировой экономики).

Можно предположить, что не существует проблемы в субституции импорта промежуточного товара: производители в обрабатывающей отрасли всегда будут предпочитать приобретать природные ресурсы внутри страны в том случае, если они есть в достаточном количестве.

Введем R[] – оператор временного лага: для некоторой динамической переменной xt, R[xt]=xt-1.

Для обрабатывающей отрасли максимальный рост выпуска Q2 может быть ограничен фактором предпочтений потребителей (показывающим потенциальную их лояльность к продукции отечественных производителей):

Q2/R[Q2]<1+ (4.1)

поэтому,



(4.2)

и

VA2=(P2-P1)Q2 (4.3)

Внутренний спрос на продукт добывающей отрасли определяется из полученного выше объема выпуска Q2.

Экспорт продукта добывающей отрасли ограничен темпом роста внешнего рынка :



(4.4)

и


(4.5)


тогда

VA1=P1Q1 (4.6)

и

Y=VA1+VA2=C+I (3.7)

3.2.4Динамика объемов инвестиций


В рамках традиционной экономической теории [Coen, Eisner, 1988] рассматриваются несколько возможных типов валового накопления:

1. инвестиции пропорциональны национальному доходу страны (аналогично кейнсианским и неоклассическим моделям) и определяются склонностью к сбережению со стороны экономических агентов [Nell, 1988]

Данный подход основан на эмпирическом исследовании, проведенном С. Кузнецом, в рамках которого было показано, что агрегированное потребление и валовое накопление в США на больших промежутках времени были пропорциональны национальному доходу.

Таким образом, для анализируемой модели

sit = si (5.1.1)

it = i (5.1.2)

2. динамически определяемая доля инвестиций в национальном доходе (аналог рынка капиталов, определяющего направление и общий размер инвестиций). Существует несколько аспектов, влияющих на динамику пропорции инвестиций и национального дохода:

а. производительность факторов в отраслях. В соответствии с моделями неоклассической теории, потребность в ресурсе будет зависеть от относительной производительности данного ресурса. Таким образом, если



(5.2)


где

Xi – некоторый ресурс типа X (M или К) для отрасли i,

MPXit – предельный продукт ресурса Xi,

то пропорции инвестиций будут зависеть от (pK1, pM1, pK2, pM2):




(5.3.1)



(5.3.2)


б. производительность отраслей. Поскольку отрасли могут делать разный вклад в национальный доход, то пропорции распределения инвестиционных ресурсов между отраслями могут определяться вкладом каждой из отраслей. В простейшем случае,

sit =VAit/Yt*s (5.4.1)

it = i (5.4.2)

В данном случае, поскольку

Iit = sitYt = s* VAit (5.5)

можно рассматривать отрасли как независимые экономики, каждая из которых финансирует свое развитие из своих собственных средств (при норме сбережения s). Таким образом, (а) не учитываются эффекты межотраслевого взаимодействия, в т.ч. «переливания» инвестиционных ресурсов между отраслями, (б) сама экономическая система отображается неадекватно, поскольку развитие каждого из секторов за собственный счет – крайне редкий вариант ее развития, как правило же, ресурсы одной отрасли используются для развития другой (что соответствует эволюционарной парадигме).

Для сценарного моделирования использовался второй подход (вариант «2а»), предполагающий изменение инвестиционных пропорций в зависимости от относительной производительности факторов в отраслях. Это позволило выявить четыре базовых сценария развития экономики (при использовании первого подхода некоторые из сценариев невыполнимы) – см. раздел 3.3.1.

Для аналитического исследования модели был выбран первый подход. Хотя предположение о фиксированных пропорциях инвестиций больше соответствует неоклассической, а не эволюционарной парадигме, его применение в модели позволило получить интересные выводы об оптимальной экономической динамике в долгосрочной перспективе - см. разделы 3.3.2 и 3.3.4.

Р
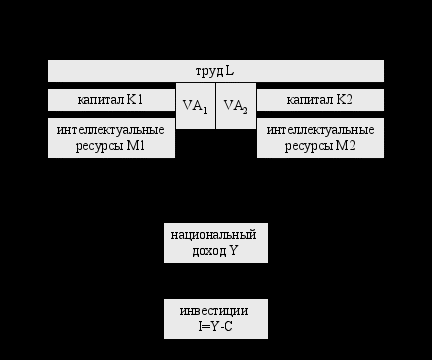
исунок 4. Схема воспроизводства ресурсов в двухотраслевой модели экономического роста


Р
исунок 5. Структура основных потоков в двухотраслевой модели