Проценко Ніна Федорівна, викладач правових дисциплін, спеціаліст вищої категорії Унавчально-методичному посібнику висвітлюються комплексно питання про закон

Вид материала

Закон

Содержание Зразки відповідей Число «13» ділиться лише на одиницю і само на себе. Щуки належать до риб. Розділ 9 ДЕДУКТИВНІ УМОВИВОДИ Умовним силогізмом Умовно категоричним силогізмом Стверджуючий модус На труні потерпілого В. ознак замерзання експертизою не встановлено. Сидоренком, визнаний недійсним. На руках, обличчі та шиї Петренка наявні садна. 9.2. Висновки із еквівалентних і одиничних умовних суджень Візерунки двох даних відбитків пальців збігаються. 9.3. Суто умовний силогізм Якщо тіло розшириться, то його не можна буде протягнути крізь отвір. Якщо існував факт

Подобный материал:

• Маляренко Світлана Олексіївна, спеціаліст вищої категорії, «старший учитель». «Нестандартні, 102.6kb.
• В. М. Захарова Використання інтерактивних методів навчання на урок, 682.45kb.
• Заступник директора з навчально-виховної роботи, вчитель математики вищої категорії,, 1763.48kb.
• Програма для вищих медичних навчальних закладів І-ІІ рівнів акредитації за спеціальністю, 2244.39kb.
• Вданій роботі подано методичні рекомендації, щодо використання методу проектів у курсі, 231.92kb.
• Програма вступного іспиту на базі освітньо-професійної програми підготовки молодшого, 194.52kb.
• Кияниця Ніна Віталіївна викладач української мови та літератури вищої категорії Тема,, 153.54kb.
• Довідка про підсумки проведення міських предметних олімпіад, 318.23kb.
• Формування ужиткових компетенцій при викладанні хімії Ряшина С.І., викладач вищої категорії,, 2216.75kb.
• Узгоджено: затверджую, 594.17kb.

ЗРАЗКИ ВІДПОВІДЕЙ


1. Вправи на визначення структури силогізмів лише на перший погляд здаються простими. Та коли при доборі та­ких вправ врахувати всі обставини, які ускладнюють про­цес відшукання складових силогізму, то доводиться визна­ти, що це вельми непроста процедура. І це пояснюється передусім тим, що не існує єдиної схеми, шаблону відшу­кання складових частин силогізму.

Аналіз будови силогізму 1а раціонально розпочати з відшукання його висновку. Висновком тут є судження «Чис­ло 13 — просте», бо саме це судження виражається го­ловним реченням¹ . До того ж це судження логічно випли­ває з інших суджень, пов'язаних з ним причинним зв'яз­ком. Про це, до речі, свідчить і сполучник «бо». Два² інших речення виражають засновки.

Оскільки суб'єкт висновку (в нашому прикладі — «чис­ло 13») завжди береться з меншого засновку, а предикат висновку (в нашому випадку — «просте») — з більшого, то судження «Ті (числа), які діляться лише на одиницю і самі на себе, називаються простими» є більшим засновком цього силогізму, а судження «Воно (число 13) ділиться лише на одиницю і саме на себе» — меншим.

Більшим терміном є поняття «прості (числа)», оскільки він займає місце предиката у висновку, а меншим — «чис­ло 13», бо цей термін виконує роль суб'єкта висновку.

Називаючи термін «ті (числа), які діляться лише на одини­цю і самі на себе» середнім, треба посилатися на те, що саме цей термін повторюється в засновках і пов'язує їх між собою.

¹ Щоправда, головним є і речення «ті числа... називаються простими». Проте воно головне стосовно підрядного означального речення «Які діляться лише на одиницю і самі на себе», котре аа своїм логічним зна­ченням рівнозначне поширеному означенню, що конкретизує ім'я, яким позначається суб'єкт відповідного засновку. Не перебуває воно і в при­чинному зв'язку з підпорядкованим йому реченням.

² Третє речення, як уже зазначалося, не виражає самостійної струк­турної одиниці силогізму — ні засновку, ні терміна.

Проте є й інші засоби встановлення структури силогізму. 2а. Ті, хто ознайомлені зі зразком розв'язання задачі 1а, погодяться, що з наведених понять можна побудувати пра­вильний силогізм, а його структуру ототожнять зі структурою силогізму, розглядуваного в першому завданні. Проте тут вар­то запропонувати й інший варіант поєднання цих понять: Всі прості числа діляться лише на одиницю і самі на себе.

Число 13 —просте._________________________________

Отже, число 13 ділиться лише на одиницю і саме на себе.

3а. Навіть тим, хто добре знає структуру та правила силогізму, відповідь на. подібне питання дається нелегко. Найраціональніше в даному разі — сказати все необхідне і обійти мовчанкою те, що не має прямого відношення до розв'язання саме цієї задачі. Основна теза міркування: цей силогізм — неправильний. Всі інші думки мають бути підпо­рядкованими обґрунтуванню цієї тези, тобто служити ар­гументами. Теоретичними аргументами виступає формулю­вання відповідного правила термінів, а фактичними — ха­рактер термінів силогізму, лише того терміна, який супе­речить відповідному правилу термінів. Все інше (якими є терміни, що не суперечать правилам термінів силогізму, тощо) не повинно відволікати увагу.

Ось така відповідь: цей силогізм — неправильний, бо в ньому порушено правило щодо середнього терміна, згідно з яким середній термін силогізму повинен бути розподіленим принаймні в одному із засновків. У цьому ж силогізмі се­редній термін («ті, що діляться лише на одиницю і самі на себе») є нерозподіленим в жодному із засновків, оскільки він (середній термін) займає місце предиката стверджувально­го судження і в більшому, і в меншому засновках.

Обґрунтовуючи неправильність наведеного силогізму графічно (з допомогою кругових схем), зазначимо, що об­сяг поняття «просте число» повністю включається в обсяг поняття «те (число), що ділиться лише на одиницю і саме на себе», оскільки поняття «просте число» є суб'єктом за­гального судження. Обсяг же поняття — «те (число) що ділиться лише на одиницю і саме на себе» — доводиться розглядати як таке, що неповністю включається¹ в обсяг

¹ Фактично названі поняття є рівнозначними (тотожними), такими, обсяги яких повністю співпадають. Проте встановити цей факт чисто формально-логічними засобами неможливо, тому предикат стверджуваль­них суджень в усіх випадках прийнято вважати нерозподіленим.

поняття «просте число», оскільки предикат стверджуваль­ного судження прийнято вважати нерозподіленим, тобто таким, що мислиться не в повному обсязі.

Сказане є підставою для такого зображення відношення обсягів суб'єкта і предиката першого засновку (хоч знання змісту цих понять свідчить про їх рівнозначність, схема 6),

Те число, що

ділиться лише на

одиницю і саме на себе



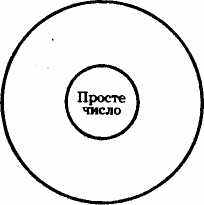
Схема 6

Залишається визначити місце обсягу поняття «число 13» стосовно обсягів понять, зображених на схемі. Щоб роз­в'язати це завдання, треба взяти до уваги лише ту інфор­мацію, яка міститься в меншому засновку: відомо, що об­сяг поняття «число 13» включається в обсяг поняття «те, що ділиться лише на одиницю і саме на себе», але нічого не відомо про його конкретну локалізацію. Враховуючи все сказане і той факт, що це поняття треба позначити точкою (як одиничне), одержимо таку схему (схема 7):

Те число, що

ділиться лише на

одиницю і саме на себе



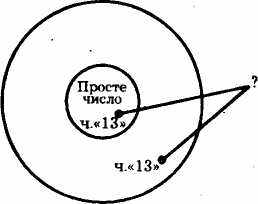
Схема 7

Схематичне зображення відношення обсягів термінів цього силогізму свідчить про те, що однозначно встанови­ти відношення обсягів крайніх термінів (тобто тих термінів, з яких робиться висновок) формально-логічними засобами неможливо. Це і є свідченням неправильності наведеного силогізму.

Багатьом таке розв'язання цієї (і подібних) задачі здаєть­ся неприйнятним. Для чого, мовляв, мудрувати, усклад­нювати прості речі? Адже «просте число» і «число, що ділиться лише на одиницю і саме на себе» — це одне й те саме. Тому знання того, що число «13» ділиться лише на одиницю і саме на себе, свідчить, що воно просте.

Проте в цьому разі не враховують, що мають справу з формальною логікою, яка навчає зв'язувати думки і робити висновки, беручи до уваги тільки ту інформацію, яка ви­ражається формою думок. А у формі даного міркування не міститься точної інформації про обсяг поняття «ті (числа), що діляться лише на одиницю і самі на себе». Обсяг його не вужчий, ніж обсяг поняття «просте число» (бо дано, що «Всі прості числа діляться лише на одиницю і самі на себе»), а такий же або ширший. За такої ситуації прийнято вва­жати, що воно має ширший обсяг (іншими словами, цей термін розглядається як нерозподілений).

Чи є якась можливість зробити цей силогізм правиль­ним? Цей — ні. Проте, вдаючись До додаткової інформації й включивши її до більшого засновку, можна одержати достовірний висновок. При цьому змін зазнає тільки більший засновок; із включаючого судження він перетвориться на виділяюче:

«Всі прості числа, і тільки вони, діляться лише на оди­ницю і самі на себе». Оскільки в цьому судженні є та інфор­мація, без якої не можна було одержати однозначного вис­новку, то є можливість побудувати правильний силогізм:

Всі прості числа, і тільки вони, діляться лише на одиницю і самі НА СЕБЕ.

Число «13» ділиться лише на одиницю і само на себе._________

Отже, число «13» — просте.

4а. Цей силогізм неправильний, оскільки в ньому по­рушено правило засновків силогізму, згідно з яким із двох заперечних засновків не можна зробити ніякого висновку.

5а. Щоб визначити фігуру цього силогізму, необхідно надати йому логічно правильної форми, тобто більший за­сновок треба поставити на перше місце, менший — на дру­ге, а висновок — на третє. Оскільки речення «Щуки диха­ють зябрами» головне, то воно виконує роль висновку в цьому силогізмі. Більший засновок тут «Всі риби дихають зябрами», бо саме з цього судження взято предикат ви­сновку («ті, що дихають зябрами»). Зрозуміло, що меншим засновком є судження «Щуки належать до риб». Про це свідчить і те, що суб'єкт висновку взято з цього судження. Після встановлення структури цього силогізму він на­буде такого вигляду:

Всі риби дихають зябрами.

Щуки належать до риб.

Отже, щуки дихають зябрами.

Цей силогізм побудований за схемою першої фігури, оскільки середній термін у ньому займає місце суб'єкта більшого засновку і предиката — меншого засновку. По­значивши засновки силогізму двома паралельними відрізка­ми прямої та сполучивши їх рисочкою, яка відповідає місцю розташування середнього терміна в засновках, одержимо схему, що нагадує зворотне зет:

А відомо, що перша фігура має саме такий вигляд.

6. Силогізм 3а побудований за схемою другої фігури. В ньому порушено правило другої фігури, згідно з яким один із засновків повинен бути заперечним.

7в. Цей силогізм побудований за схемою першої фігу­ри. В ньому порушено правило першої фігури, згідно з яким менший засновок повинен бути стверджувальним.

8. Силогізм 7а має модус АП. Про те, що більший засновок у цьому силогізмі є загальностверджувальним суд­женням, свідчать кванторне слово «всі» і зв'язка «є». Мен­ший засновок і висновок є частковостверджувальними суд­женнями. Про це свідчать відсутність кванторного слова перед суб'єктами цих суджень і наявність у них зв'язки «є». За відсутності кванторного слова лише суб'єкт одиничного судження мислиться в повному обсязі.

9а. Модус АЕЕ суперечить правилу першої фігури, згідно з яким менший засновок повинен бути стверджу­вальним.

96. Модус ІАІ суперечить обом правилам другої фігури. Більший засновок тут є частковим судженням (а він пови­нен бути загальним); обидва засновки в цьому силогізмі є стверджувальними, а згідно з вимогою одного із правил другої фігури, один із засновків повинен бути заперечним.

9в. Модус АЕЕ суперечить правилам третьої фігури си­логізму, згідно з якими менший засновок повинен бути стверджувальним судженням, а висновок — частковим. У цьому ж модусі менший засновок —заперечний, а висно­вок — загальний.


Розділ 9 ДЕДУКТИВНІ УМОВИВОДИ (продовження)


9.1. Умовно-категоричний силогізм

(ІНШІ ВИДИ ОПОСЕРЕДКОВАНИХ ДЕДУКТИВНИХ УМОВИВОДІВ)

Крім простих категоричних силогізмів, які складаються тільки з категоричних суджень, є й інші види опосередко­ваних дедуктивних умовиводів, до складу яких входять такі види суджень, як умовні та розділові.

Умовним силогізмом називається силогізм, у якому один або обидва засновки є умовними судженнями. Розрізняють два види умовних силогізмів: умовно-категоричний силогізм і чисто умовний силогізм.

Умовно категоричним силогізмом називається силогізм, у якому більший засновок є судженням умовним, а менший — категоричним. Наприклад:

Якщо правовідносини належать до цивільного права, то суперечка підлягає судовому розгляду.

Ці правовідносини належать до цивільного права.___________

Отже, суперечка у цьому випадку має бути розв'язана у судовому порядку.

Логічною основою висновків умовнокатегоричного сило­гізму є така аксіома: ствердження основи неодмінно призво­дить до ствердження наслідку, а заперечення наслідку — до заперечення основи.

Це положення виражає такий об'єктивно існуючий зв'я­зок між причиною і наслідком: 1) певна причина неодмінно викликає певний наслідок і 2) наслідок не може виникнути без причини з нічого. Тому, якщо існує причина, то має існу­вати і її наслідок; якщо гаданий наслідок не існує, то це означає, що не існує й причини, котра викликає цей наслідок. Наприклад, якщо тіло нагріти (причина), то воно обов'язково розшириться (наслідок), а якщо цей наслідок відсутній, то відсутня його причина (нагрівання).

Подібну умовну залежність ми спостерігаємо також між явищами співіснуючими та явищами, пов'язаними у певній послідовності у часі.

Залежно від того, який хід руху думки від ствердження основи до ствердження наслідку або від заперечення наслідку до заперечення основи, розрізняють два модуси умовно-кате­горичного силогізму: стверджуючий та заперечний.

Стверджуючий модус — це такий умов­но-категоричний силогізм, у якому в меншому засновку ствер­джується основа, а у висновку — наслідок більшого заснов­ку. Формула модусу:

Якщо А, то В

А____

Отже, В.

За допомогою символів математичної логіки цей модус відображають так:

А—>В . А

В.

У стверджуючому модусі від істинності (існування) осно­ви ми йдемо до істинності (існування) наслідку. Хід умови­воду тут ґрунтується на положенні: ствердження основи веде до ствердження наслідку.

Менший засновок стверджуючого модусу за якістю не обо­в'язково є ствердним, він може бути й заперечним. Згідно з цим стверджуючий модус має такі чотири різновиди:

1. Якщо А, то В

А або А -> В • А

В В.

2. Якщо не А, то В

не А або ~А—>В • ~А

В В.

3. Якщо А, то не В

_А_ або А->~В • А

не В ~В

4. Якщо не А, то В

не А або ~А ->~В • ~А

не В ~В.

Заперечний модус (тойиз іоііепз) — це такий умовно-категоричний силогізм, у котрому у меншому засновку за­перечується наслідок, а у висновку — основа більшого за­сновку. Формула модусу:

___не В__ або інакше: А->В • ~В

Отже, не А ~А

У заперечному модусі у меншому засновку заперечується істинність (існування наслідку) більшого засновку, йдеться про те, що в цьому випадку немає такого наслідку, котрий указано в умовному судженні. У висновку висловлюється думка про те, що в цьому випадку не було (або немає) і самої основи більшого засновку. Наприклад:

Якщо смерть потерпілого настає від замерзання, то на його трупі

мають бути ознаки замерзання.

На труні потерпілого В. ознак замерзання експертизою не встановлено.

Отже, смерть потерпілого В. настала не від замерзання.

У заперечному модусі ми робимо висновок від хибності (відсутності) наслідку до хибності (відсутності) основи. Та­кий рух думки визначається положенням (аксіомою): запе­речення наслідку є заперечення основи.

Заперечуючий модус має такі чотири різновиди:

1. Якщо А, то В

не В або А -> В • ~В

не А А.

2. Якщо не А, то В

не В або ~А -> В• ~В

А А.

3. Якщо А, то не В

В_ або А ->~В • В

не А ~А.

4. Якщо не А, то не В

_В_ або ~А ->~В • В.

А А

Обидва розглядувані модуси (стверджуючий і заперечний) правильні, їх висновки, що випливають із засновків немину­че, — достовірні. Правомірним є запитання: чи можна в умовно-категоричному силогізмі робити висновок від хиб­ності основи до хибності наслідку і від істинності наслідку до істинності основи? Відповідь на це запитання логіка дає негативну. Зумовлено це ось чим. Зв'язок причини й наслідку (дійсності), як правило, неоднозначний. Один і той же наслідок може бути викликаний не однією, а різними причинами. На­приклад, пожежа (наслідок) може виникнути унаслідок підпа­лу, через несправність електропроводки, удару блискавки, якогось нещасного випадку; подряпини та садна на тілі підоз­рюваного можуть бути наслідком його боротьби з жертвою, але можуть бути й наслідком якоїсь іншої причини.

Схематично відношення причини і наслідку можна відоб­разити так:

х ->

Причини у -> А (наслідок).

z ->

Якщо цю схему виразити у вигляді суджень, то вислови­мо три такі умовні судження:

1. Якщо є х, то є А

2. Якщо є у, то є А.

3. Якщо є z, то о А тобто якщо є причина, то є і наслідок.

Із наведеного видно також, що якщо немає, наприклад, причини х, то це ще не означає, що нема й наслідку А; воно могло бути викликане причиною у або причиною z. Л якщо існує наслідок А, то з цього неминуче не випливає, що в цьому випадку існує причина х; наслідок міг бути результатом при­чини у або z. Тому умовиводи від заперечення даної основи до заперечення наслідку і від ствердження наслідку до ствер­дження певної основи дають знання не достовірні, а тільки більш-менш імовірні або хибні. Наприклад:

Якщо договір купівлі-продажу будинку укладений не в нотаріальній

формі, то він визнається недійсним.

Договір купівлі-продажу будинку, укладений Петренком і

Сидоренком, визнаний недійсним.______________________

Отже,...

Тут у меншому засновку стверджується наслідок більшо­го засновку, тому не можна зробити істинного висновку про те, що даний договір укладений не в нотаріальній формі, він міг бути визнаний недійсним з якоїсь іншої причини, на­приклад тому, що документи домовласника виявилися підроб­леними.

Висновки від існування наслідку до існування основи і від відсутності основи до відсутності наслідку не містять до­казової сили, за їхньої допомоги не можна обґрунтувати кінце­вих висновків із судової справи. Але, оскільки вони все ж можуть давати приблизні знання, ними часто користуються у практиці розслідування кримінальних справ під час вису­вання версій.

Наприклад, на місці вчиненого злочину виявлено труп із слідами боротьби. Слідчий припускає, що сліди боротьби ма­ють залишитися і на тілі злочинця. У ході розслідування спра-ии стає відомо, що у Петренка на руках, обличчі і шиї наявні садна й подряпини. Природно припустити, що Петренко при­четний до вчиненого злочину. Така версія з логічного боку є висновком від існування наслідку до існування основи:

Якщо в момент скоєння злочину потерпілий залишив садна

й подряпини на тілі злочинця, то вони мають бути на ньому.

На руках, обличчі та шиї Петренка наявні садна.

Отже, вони залишені потерпілим.

Здобутий висновок тільки імовірний, оскільки садна у Петренка могли утворитися за обставин, котрі не пов'язані із цим злочином.


9.2. Висновки із еквівалентних і одиничних умовних суджень

Особливість еквівалентних умовних суджень полягає в тім, що в них зв'язок між основою й наслідком однозначний: основі відповідає такий і тільки такий наслідок, а наслідок може бути тільки і тільки даний основі. Тому в умовно-кате­горичних силогізмах, більший засновок котрих є умовне ек­вівалентне судження, робити висновок можна не тільки від істинності основи до істинності наслідку і від хибності на­слідку до хибності основи, а й від ствердження наслідку до ствердження основи та від заперечення основи до заперечен­ня наслідку. Наприклад:

Якщо два відбитки пальця залишені однією й тією ж особою, то

їхні візерунки будуть збігатися.

Візерунки двох даних відбитків пальців збігаються.

Отже, вони залишені однією й тією ж особою.

Схема цього умовиводу така:

А~В • В

А.

У цьому умовиводі від заперечення основи зроблено пе­рехід до заперечення наслідку. Висновок, як і в першому прикладі, є правомірним, оскільки більший засновок є еквіва­лентним умовним судженням.

В одиничних умовних судженнях основа й наслідок та­кож перебувають в однознач-ному зв'язку. Тому в умовиво­дах, побудованих із одиничних умовних суджень, правомірні висновки від істинності наслідку до істинності основи і від хибності основи до хибності наслідку. Наприклад:

Якщо ніж, знайдений біля трупа потерпілого, виготовлений із коси, виявленої в обвинувачуваного, то заглибина на обусі цього ножа за розміром і взаємним положенням має повністю збігатися із виступом на обусі коси.

Експертизою встановлено, що заглибина на обусі ножа за розміром і положенням повністю збігається з виступом на обусі коси, вилученої в обвинувачуваного.

Отже, ніж, виявлений біля трупа потерпілого, виготовлений із коси, вилученої в обвинувачуваного.

Тут від існування наслідку ми перейшли до існування основи. Правомірність такого висновку зумовлена характе­ром більшого засновку, що є в цьому випадку одиничним умовним судженням.


9.3. Суто умовний силогізм

Суто умовний силогізм — це такий силогізм, у котрому засновки є судженнями умовними. Наприклад:

Якщо дане тіло нагріти, то воно розшириться.

Якщо тіло розшириться, то його не можна буде протягнути крізь отвір.

Отже, якщо дане тіло нагріти, то його не можна буде протягнути крізь цей отвір.

Формула цього силогізму:

Якщо А, то В

Якщо В, то С_____

Отже, якщо А, то С.

За допомогою символів математичної логіки суто умов­ний силогізм можна записати так: (А—>В)(В—>С)—>(А—>С).

Суто умовний силогізм відображає такі причинно-наслідкові зв'язки трьох явищ, коли одне явище є причиною друго­го, а це друге виступає водночас причиною третього явища.

Випадки зв'язку, які мільярди разів повторюються на практиці, таких трьох явищ приводять нашу свідомість до переконання, що можна логічним шляхом установити відношення між першим (А) і третім (С) явищами на основі друго­го (В), безпосередньо пов'язаного з ними причинно-наслідковим зв'язком. Це переконання нашої свідомості закріпилося у практиці мислення у формі суто умовного силогізму.

Як видно із формули і наведеного прикладу, в цих умови­водах умовними є не тільки засновки, а й висновок. У більшому засновку висловлюється основа і наслідок, що з неї випли­ває: якщо А, то В. У меншому засновку йдеться про те, що якщо існує наслідок більшого засновку, то з нього, як із осно­ви, в свою чергу, випливає певний наслідок: якщо В, то С. У висновку встановлюється відношення, існуюче між основою більшого і наслідком меншого засновку, тобто між основою і наслідком результату: якщо А, то С. Пов'язуючою ланкою між засновками виступає наслідок (В) першого і основа (В) другого засновку. Вона виконує роль середнього терміна і до висновку не входить.

Висновок чисто умовного силогізму ґрунтується на такій аксіомі: результат наслідку є наслідок основи.

Суто умовний силогізм дає змогу від одного факту або явища перейти до другого, причинно пов'язаного з першим, а від другого — до третього і таким чином установити не дану безпосередню умовну залежність третього факту або явища від першого, вихідного явища.

Ця особливість суто умовних умовиводів широко вико­ристовується у слідчій практиці для виявлення, аналізу і оцінки доказових фактів та джерел доказів. Справді, якщо факти, ознаки, обставини причинно пов'язані між собою, то з визнанням одного факту ми маємо визнати існування (або неіснування) другого факту, а з наявністю (або відсутністю) третього факту і т. д. За вихідне (причину, основу) береться якийсь факт, повідомлений свідком, потерпілим, обвинувачу­ваним, експертом, або факт, установлений слідством, і з нього за формою суто умовного силогізму виводять інші факти. Умовивід має такий вигляд:

Якщо існував факт А, то мав бути і факт В.

Якщо існував факт В, то має існувати і факт С.____

Отже, якщо існував факт А, то має існувати і факт С.

Наприклад, за кримінальною справою про аварію поїзда слідчий від відомого факту (1 вересня о 2 год. 52 хв. ГЕС припинила подавати струм залізниці) дійшов висновку, що свідчення машиніста 3. і його помічника, нібито вони не проїздили сигналів заборони (жовтого кольору світлофорів), не відповідають тому, що було насправді. Умовивід будувався так:

Якщо 1 вересня о 2 год. 52 хв. ГЕС, що живила електроенергією залізницю, припинила подавати їй струм, то де неминуче мало викликати бездіяльність усієї системи автоблокування. Якщо автоблокування вийшло з ладу, то після проїзду першого недіючого світлофора автостоп потягу мав подати звуковий сигнал пильності.

Якщо автостоп потягу подав звуковий сигнал небезпеки, то машиніст 3. і його помічник мусили б помітити недіючі світлофори.___________________________

Отже, якщо 1 вересня о 2 год. 52 хв. ГЕС припинила подавати залізниці електричний струм, то машиніст 3. і його помічник мусили б помітити недіючі світлофори.