Учебно-методический комплекс информационные ресурсы дисциплины методические указания к лабораторно-практическим работам санкт-Петербург

Вид материала

Учебно-методический комплекс

Содержание уравнение электрического равновесия цепи первичной обмотки уравнен6ие электрического равновесия цепи вторичной обмотки уравнен6ие электрического равновесия магнитодвижущих сил в пределах магнитопровода трансформатора уравнен6ие электрического равновесия токов в узле контура намагничивания U на внутреннем сопротивлении приведенного трансформатора (изменение напряжения) можно вычислить по следующей формуле: u =  (u 3.5. Вычисление коэффициента полезного действия (КПД) трансформатора 3.6. Для описания конструкции и назначения

Подобный материал:

• Учебно-методический комплекс для студентов специальности «Реклама» Санкт-Петербург, 284.63kb.
• Методические указания к лабораторно-практическим занятиям для студентов очного и заочного, 620.25kb.
• Методика обучения изобразительной деятельности детей с проблемами в развитии Учебно-методический, 1422.44kb.
• Практикум (ч Деревообработка) Учебно-методический комплекс дисциплины Бийск бпгу имени, 1777.11kb.
• Учебно-методический комплекс по дисциплине " мировые информационные ресурсы " для специальности, 184.11kb.
• Учебно-методический комплекс по дисциплине " мировые информационные ресурсы " для специальности, 187.55kb.
• Учебно-методический комплекс по специальности: 030602. 65 Связи с общественностью Санкт-Петербург, 228.89kb.
• Учебно-методический комплекс по специальности: 030602. 65 Связи с общественностью Санкт-Петербург, 199.1kb.
• Учебно-методический комплекс по дисциплине психология искусства по направлению 521000, 624.8kb.
• Учебно-методический комплекс по специальности: 030602. 65 Связи с общественностью Санкт-Петербург, 214.6kb.

Полная система уравнений электрического равновесия трансформатора в соответствии с приведенной на рис. 1.5 Т-образной схемой замещения выглядит следующим образом:

• уравнение электрического равновесия цепи первичной обмотки:

U₁= - E₁ + r₁I₁ + j x₁I₁

• уравнен6ие электрического равновесия цепи вторичной обмотки:

U₂ = E₂ – r₂I₂ - j x₂I₂


или для приведенных величин:


U^/₂ = E^/₂ – r^/₂I^/₂ - j x^/₂I^/₂

• уравнен6ие электрического равновесия магнитодвижущих сил в пределах магнитопровода трансформатора:

I₁ W₁ + I₂ W₂ = I₀ W₁

• уравнен6ие электрического равновесия токов в узле контура намагничивания:

I₁ + I^/₂ = I₀ = I_0а + I_0р


Взаимосвязь и взаимовлияние синусоидальных электрических и магнитных величин с одинаковым периодом повторения (с одинаковой частотой f) проще и нагляднее анализировать при помощи так называемых векторных диаграмм.

При этом:

• на векторных диаграммах изменяющиеся синусоидально величины изображают в виде векторов, длины которых равны в определенном масштабе амплитуде отображаемых величин;
  
• все вектора, относящиеся к синусоидам одинаковой частоты, изображаются на векторной диаграмме вращающимися с циклической частотой ₀ = 2f относительно общего центра;
  
• за положительное направление вращения векторов принято левое направление (направление «против часовой стрелки»);
  
• углы, которые векторы образуют (с учетом положительного направления вращения) с начальной (нулевой) линией, равны фазовым (временным) сдвигам соответствующих синусоид относительно начала координат;
  
• углы, которые векторы образуют (с учетом положительного направления вращения) друг с другом, равны фазовым (временным) сдвигам между соответствующими синусоидами.
  

Обычно с нулевой линией отсчета на векторных диаграммах совмещают один из векторов, соответствующий какой либо величине (параметру) наиболее общей для различных участков рассматриваемой схемы или устройства.

При изображении и анализе векторных диаграмм трансформаторов за базовый вектор удобнее всего принять вектор основного магнитного потока Ф, имеющего потокосцепление со всеми обмотками трансформатора.

В качестве исходных данных для построения векторной диаграммы необходимо иметь все параметры соответствующей схемы замещения и соответствующие уравнения электрического равновесия.

На основании представленных выше Т-образной схемы замещения (см. рис. 1.5) и системы уравнений электрического равновесия цепей трансформатора на рисунке 1.7 представлена век­торная диаграмма для режима работы трансформатора со смешанной активно-индуктивной нагрузкой.

При построении векторной диаграммы рис. 1.7 использованы следующие обозначения и применены следующие правила для её построения.

Ф – вектор основного магнитного потока, создаваемого результирующей МДС первичной и вторичной обмоток трансформатора: является базовым вектором.

Е₁– вектор ЭДС, наводимой в первичной обмотке основным магнитным потоком: в соответствии с законом электромагнитной индукции отстает от вектора Ф на 90⁰.

Е₂^ (равная Е₁) – «приведенная» ЭДС вторичной обмотки: в соответствии с законом электромагнитной индукции также, как и Е₁ отстает от вектора Ф на 90⁰.

I₀– вектор тока холостого хода: опережает вектор основного магнитного потока на «гистерезисный» угол .

I₂^ - «приведенный» ток вторичной цепи (ток нагрузки): определяется в соответствии с уравнением (3.52), вследствие активно-индуктивного характера цепи отстает от вектора Е₂^ на угол ₂.

I₁– ток статорной обмотки: определяется в соответствии с уравнением (3.53) как сумма векторов I₀ и I₂^.

I₁r₁– вектор падения напряжения на активном сопротивлении r₁ первичной обмотки от протекающего по ней тока I₁: соввпадает по фазе с вектором тока I₁.

jI₁x₁ – вектор падения напряжения на индуктивном сопротивлении x₁ первичной обмотки от протекающего по ней тока I₁: опережает вектор тока I₁ на 90⁰.

U₁ – вектор напряжения сети: получается в соответствии с уравнением (3.50) как результат сложения векторов - Е₁, I₁r₁ и j I₁x₁.

I₂^r₂^ – вектор падения напряжения на «приведенном» сопротивлении r₂^ вторичной обмотки от протекающего по ней тока I₂^: соввпадает по фазе с вектором тока I₂^.

jI₂^x₂^ – вектор падения напряжения на «приведенном» индуктивном сопротивлении x₂^ вторичной обмотки от протекающего по ней тока I₂^: опережает вектор тока I₂^ на 90⁰.

U₂^ – вектор выходного напряжения трансформатора: получается в соответствии с уравнением (3.52) как результат вычитания из вектора Е₂^, векторов jI₂^x₂^ и I₂^r₂^.





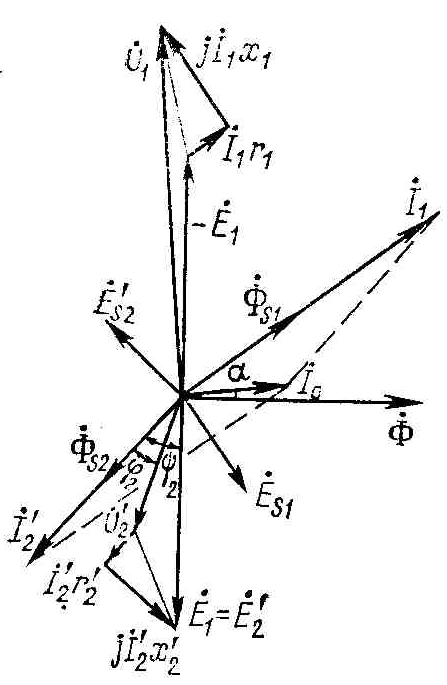
Рис. 1.7. Векторная диаграмма трансформатора при активно-индуктивной нагрузке.


Токи I₁ и I₂^создают вокруг витков первичной и вторичной обмоток потоки рассеяния Ф_S1 и Ф_S2, векторы которых совпадают с векторами создающих их токов (так как потоки рассеяния замыкаются по воздуху и «гистерезисный» угол отсутствует). Потоки рассеяния Ф_S1 и Ф_S2 создают ЭДС E_S1 и E_S2, векторы которых отстают от векторов вызвавших их магнитных потоков на угол 90⁰. Важно отметить, что векторы E_S1 и E_S2 в расчетной практике не применяются и заменяются (в соответствии с принципом компенсации) падениями напряжения (с противоположными знаками) на соответствующих индуктивных сопротивлениях рассеяния (в данном случае векторами: - jI₁x₁ и - jI₂^x₂^).^

Векторная диаграмма трансформатора при чисто активной нагрузке потребителя изображена на рис. 1.8а. Она отлича­ется от приведенной выше векторной диаграммы рис. 1.7 только тем, что угол ₂ между векторами выходного напряжения U₂^, и током вторичной обмотки (нагрузки) I₂^ равен нулю (индуктивная составляющая тока вторичной обмотки скомпенсирована).

Векторная диаграмма трансформатора при значительной ем­костной нагрузке потребителя представлена на рис. 1.8б. Здесь вектор тока вторичной обмотки I₂^ опережает ЭДС Е₂^. В ре­зультате и ток первичной обмотки I₁ получается опережающим по отношению к напряжению сети U₁.





Рис. 1.8. Векторные диаграммы трансформатора при чисто активной (а) и активно-емкостной (б) нагрузках.


3.4. Вычисление изменения напряжения трансформатора


Изменением напряжения трансформатора называется выраженное в процентах изменение его выходного (вторичного) напряжения при изменении тока нагрузки от нуля до номинального значения.

Падение напряжения  U на внутреннем сопротивлении приведенного трансформатора (изменение напряжения) можно вычислить по следующей формуле:

u =  (u_aCos₂ + u_r Sin₂ )

где: u_a - активная составляющая напряжения короткого замыкания;

u_r - реактивная составляющая напряжения короткого замыкания.

 – коэффициент загрузки (в номинальном режиме  = 1);

₂ – угол нагрузки.

Обратите внимание на то, что в последней формуле указаны действующие значения рассматриваемых напряжений.


3.5. Вычисление коэффициента полезного действия (КПД) трансформатора

Коэффициент полезного действия  это отношение полезной активной энергии (работы) ко всей затраченной. Разделив величину активной энергии или работы на время, за которое эта работа совершена, получим значение активной мощности и, соответственно, коэффициент полезного действия можно рассчитывать как соотношение полезной Р₂ и всей затраченной Р₁ активных мощностей.

Активную мощность P ₂ в нагрузке трансформатора (полезную мощность) можно рассчитать по следующей формуле:


P ₂ = U₂ I₂ Cos ₂


где Cos ₂ – коэффициент мощности приёмника (нагрузки) на вторичной стороне трансформатора;

Всю активную мощность, потребляемую трансформатором из сети, находим как:

P ₁ = U₁ I₁ Cos ₁


И, наконец:

 = Р₂/ Р₁


Однако, ввиду соизмеримости величин Р₂ и Р₁ (КПД крупных трансформаторов достигает величин 0,97 – 0,98), любая неточность в определении значений Р₂ и Р₁ может приводить к большим погрешностям в определении КПД. Поэтому, в теории электрических машин приняты и иные методы и приемы для расчета КПД трансформатора.

Если ввести понятие коэффициента загрузки трансформатора , под которым понимается отношение тока вторичной обмотки, который трансформатор действительно отдает нагрузке, к его номинальному значению, то полезная мощность трансформатора может быть вычислена как Р₂ = S_н Cos ₂. Чтобы получить затраченную мощность, надо прибавить к этой полезной мощности потери мощности в стали, которая равна мощности, найденной в опыте холостого хода Р_х и потери мощности на нагревание проводов обмоток (потери в меди), которая определяется из мощности Р_к , полученной в опыте короткого замыкания. Уточним, что в опыте короткого замыкания найдены потери мощности в меди при номинальном токе. Мощность, нагревания проводов пропорциональна квадрату тока, который по ним протекает или квадрату коэффициента загрузки трансформатора. Так что потери мощности в меди при заданной нагрузке равны ^Р_к. В результате, для расчета коэффициента полезного действия имеем формулу:


= k _нг P_2н  ( k _нг P_2н + Р_хх + k _нг²Р_К)


3.6. Для описания конструкции и назначения трансформатора по его буквенно-цифровому обозначению необходимо изучить [1], ч.1, с.с. 48-57; ч.2, с.с.14-24.