Geum.ru

Министерство образования и науки Российской Федерации Ростовский Государственный Университет

Вид материалаДокументы

Содержание


ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ ВРАЩЕНИЯ ТЯЖЕЛОГО АСИММЕТРИЧЕСКОГО ВОЛЧКА С НЕПОДВИЖНОЙ НИЖНЕЙ ТОЧКОЙ Новакович А.А., Кириленко О. В.
Подобный материал:
1   ...   42   43   44   45   46   47   48   49   ...   75


ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ ВРАЩЕНИЯ ТЯЖЕЛОГО АСИММЕТРИЧЕСКОГО ВОЛЧКА С НЕПОДВИЖНОЙ НИЖНЕЙ ТОЧКОЙ

Новакович А.А., Кириленко О. В.

Ростовский государственный университет, физический факультет




Задача университетского образования для специалистов с квалификацией: “Физик. Преподаватель физики, математики и информатики” - дать знания, позволяющие не только проводить уроки физики и информатики по программе средней школы, но и выходящие за рамки школьной программы. В частности умение ставить и решать задачи повышенной сложности с использованием персональных компьютеров и современных прикладных программ. Представленный доклад основан на материале дипломной работы Кириленко О.В., в которой решена задача об устойчивости вращения тяжелого (т.е. находящегося во внешнем, однородном гравитационном поле) асимметрического волчка с неподвижной нижней точкой. Полученный результат может быть использован в учебном курсе, как дополнительный материал при изучении теоретической механики в университетах и технических ВУЗах.

Предполагалось, что ось вращения волчка совпадает с одной из его осей инерции и ориентирована вертикально. Для решения были использованы уравнения Эйлера [1], проведены их линеаризация, и исследование динамики изменения малых возмущений движения во времени. Математический пакет Maple оказался необычайно удобен в данном случае. В работе указаны геометрия и размеры асимметрических волчков: а) вращение которых не устойчиво ни при какой угловой скорости, б) имеющих область устойчивого вращения, ограниченной снизу минимальным значением угловой скорости и в) областью устойчивого вращения которых является узкая полоса значений угловых скоростей. Существование узкой полосы частот устойчивости тяжелого асимметрического волчка вполне нетривиально. Этому случаю соответствует промежуточное значение момента инерции волчка относительно оси вращения. Известно, что вращение свободного асимметрического волчка в этом случае неустойчиво, и его формально можно рассматривать как предельный случай тяжелого волчка в пределе устремления ускорения свободного падения к нулю, или что, эквивалентно в случае бесконечного значения угловой скорости вращения. Напротив, при малом значении величины угловой скорости вращения, волчок представляет собой физический маятник в положении неустойчивого равновесия. Таким образом, ни при малых, ни при больших значениях угловой скорости вращения, не ожидается возникновения явления устойчивости. По этой причине возникновение полосы частот устойчивого вращения тяжелого асимметрического волчка факт нетривиальный. Полученные результаты вполне заслуживают отражения в современном курсе теоретической механики. Следует отметить, что ни в одном учебнике по теоретической механике данный результат не отражен.

Применим уравнения Эйлера к задаче об устойчивости вращения тяжелого асимметрического волчка с неподвижной нижней точкой:

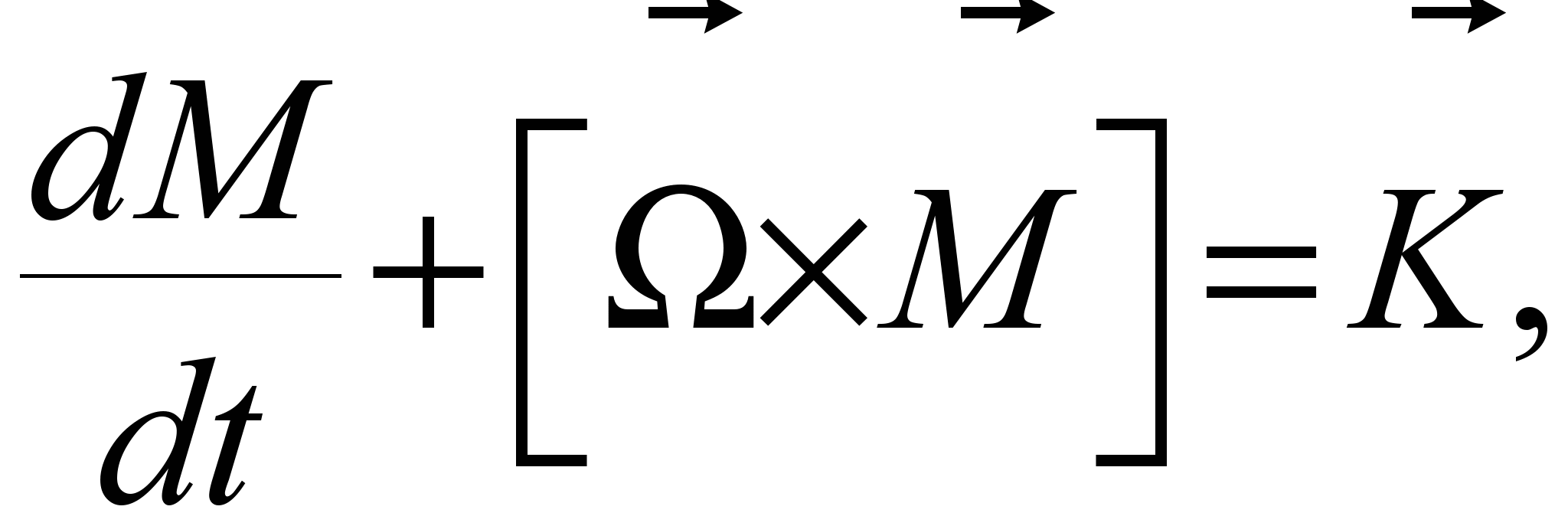(1)

где 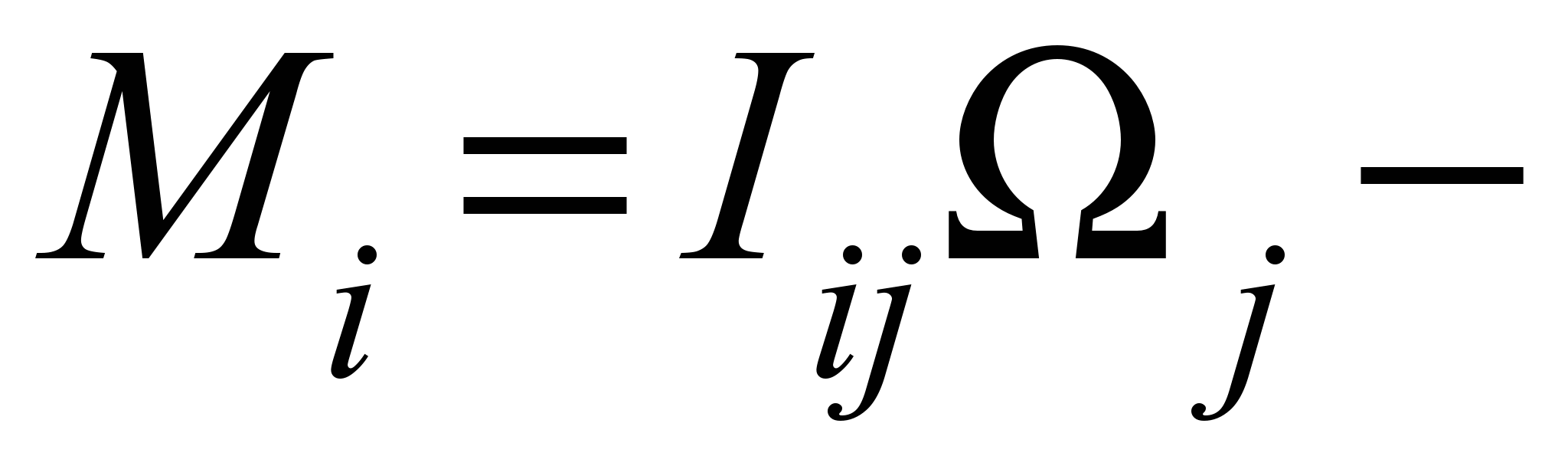момент импульса волчка, 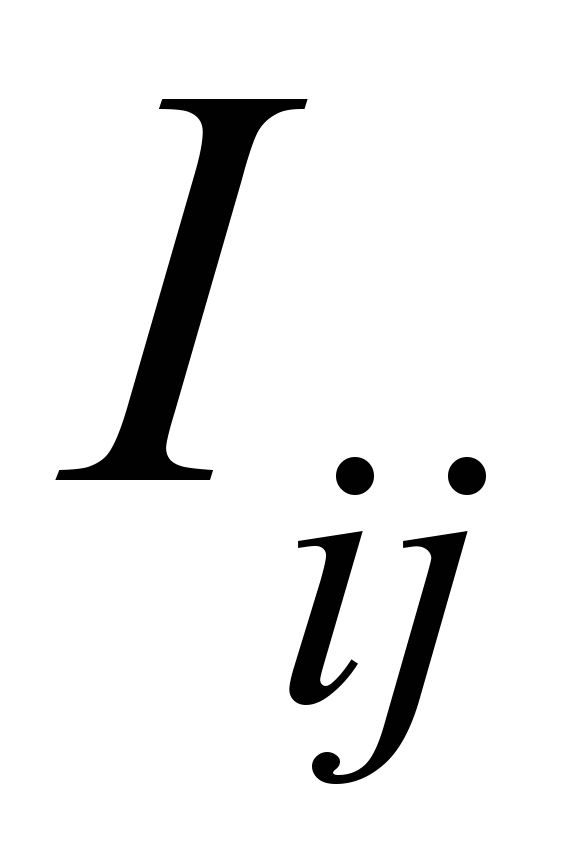- тензор моментов инерции, имеющий диагональный вид в подвижной системе координат. 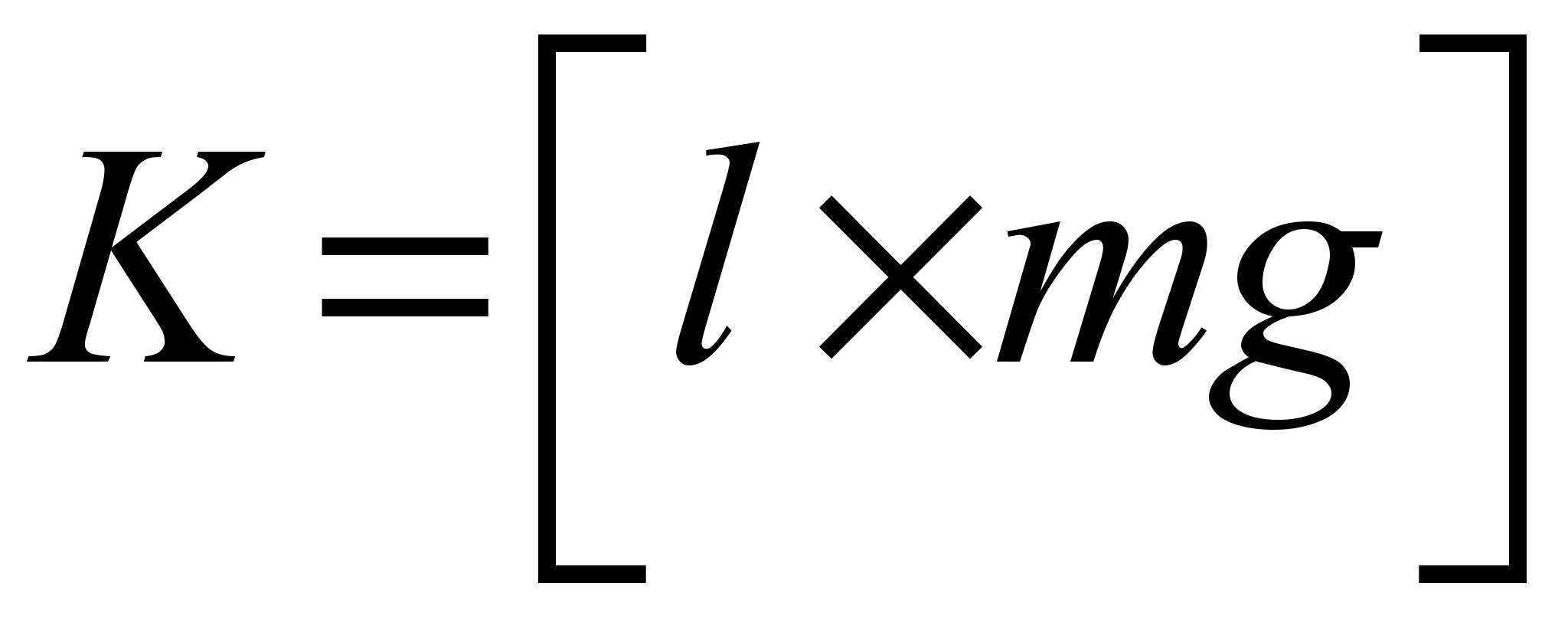- момент сил. Радиус-вектор центра масс: 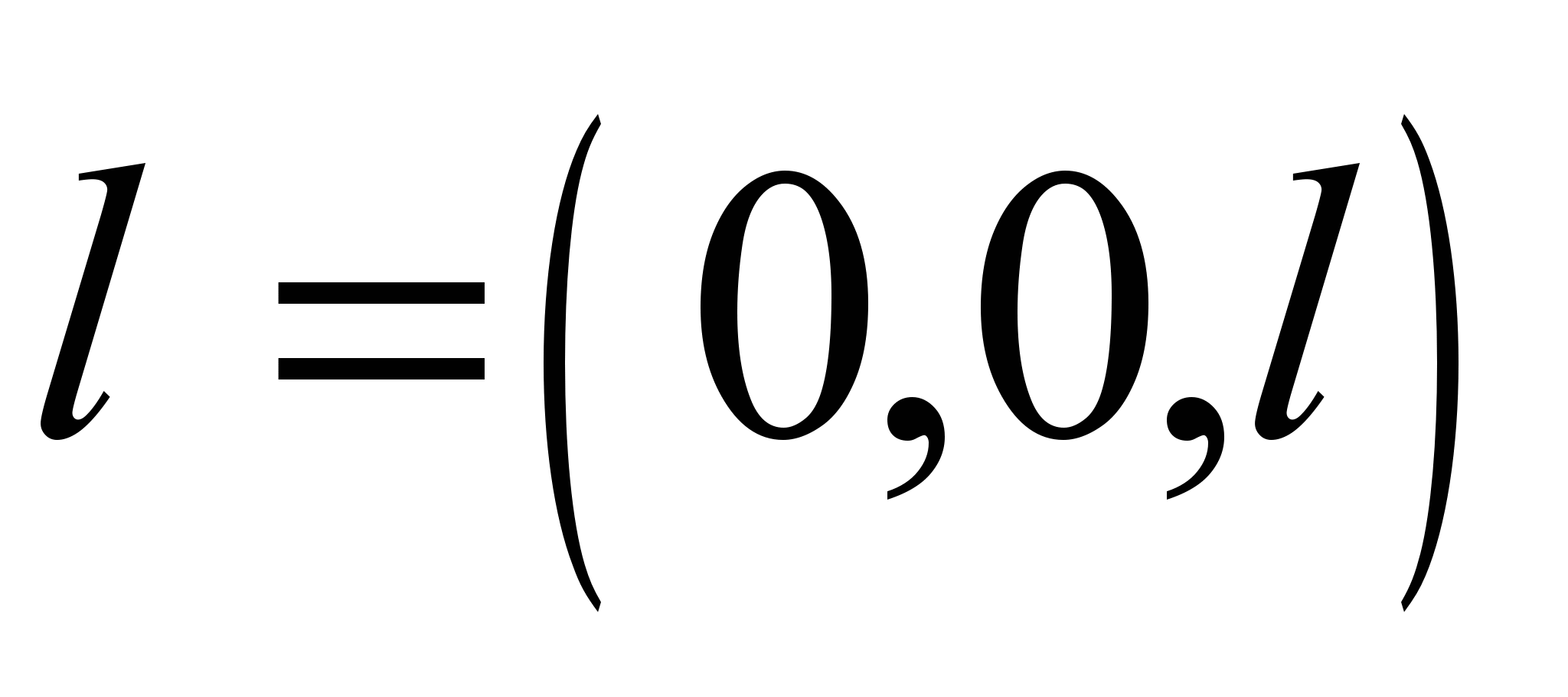в подвижной системе координат фиксирован.

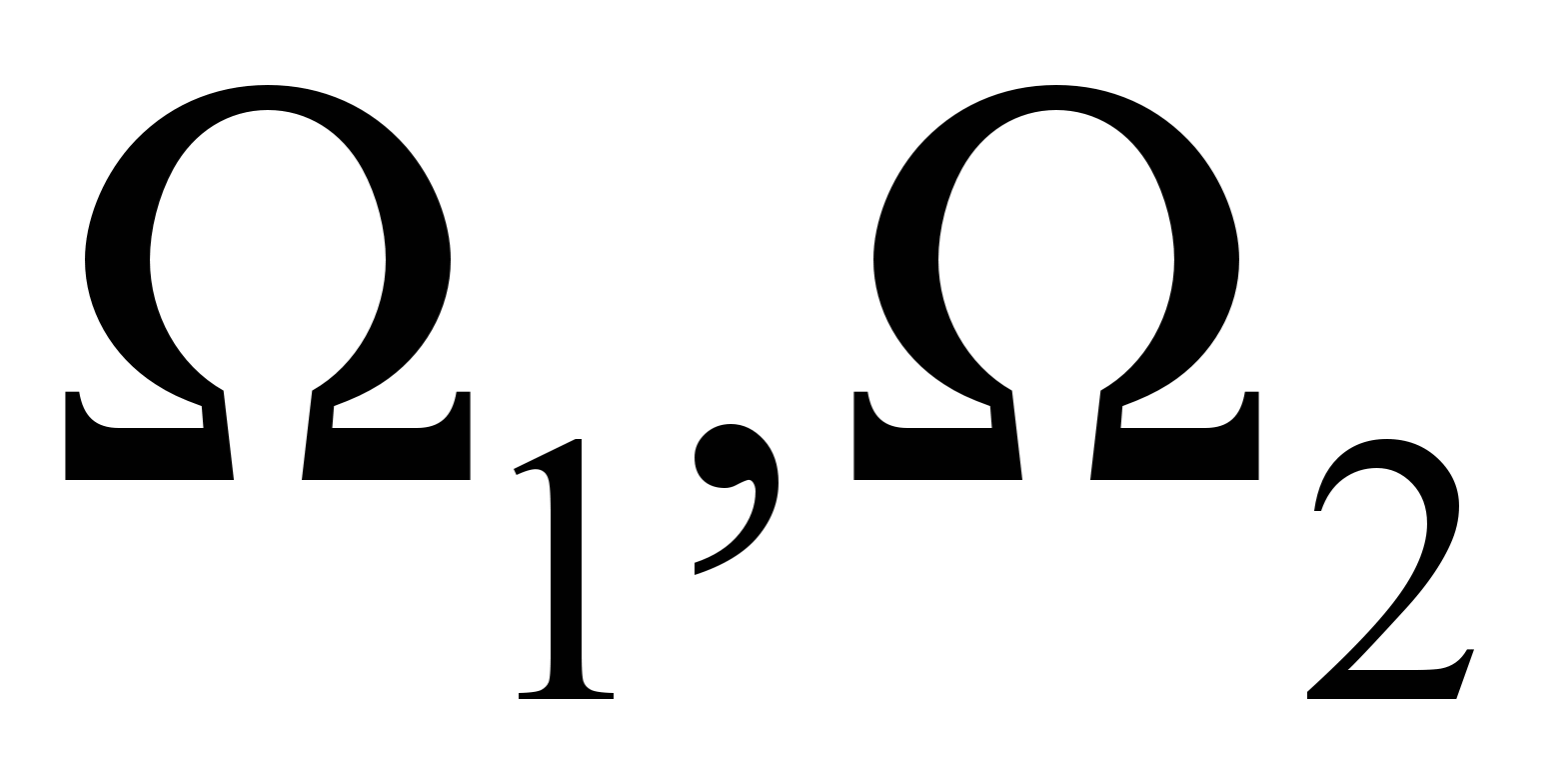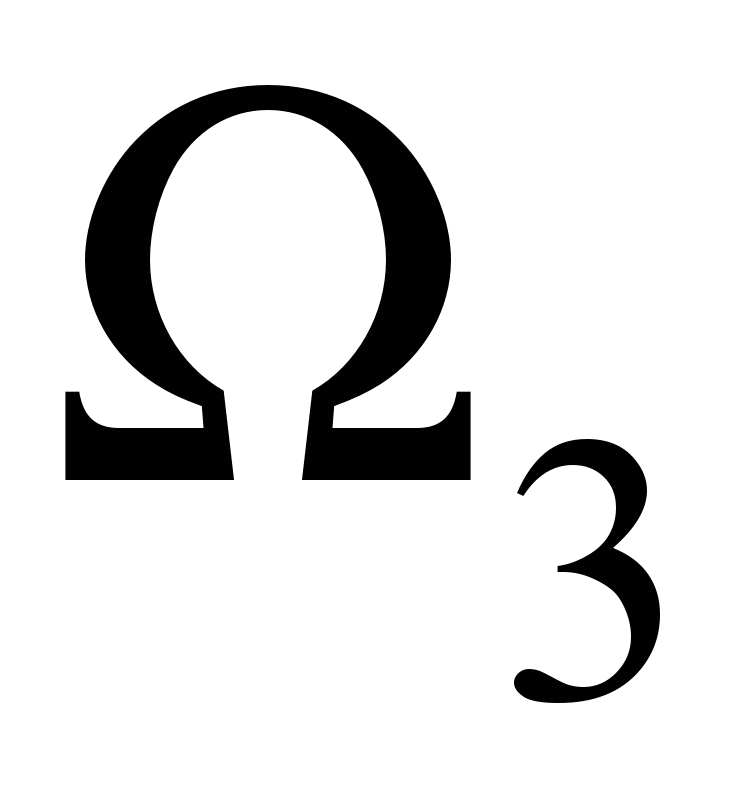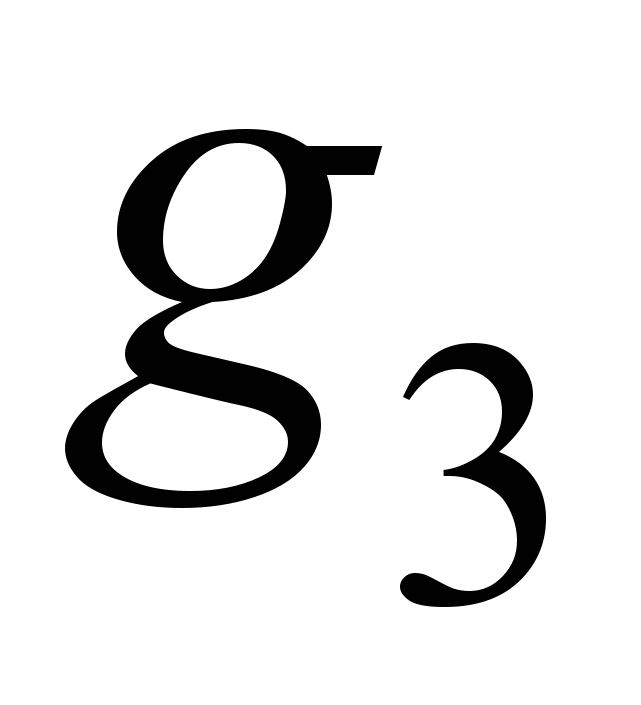Будем считать, что компоненты угловой скорости: малы по сравнению с , компоненты малы по сравнению с , тогда с точностью до величин первого порядка малости, 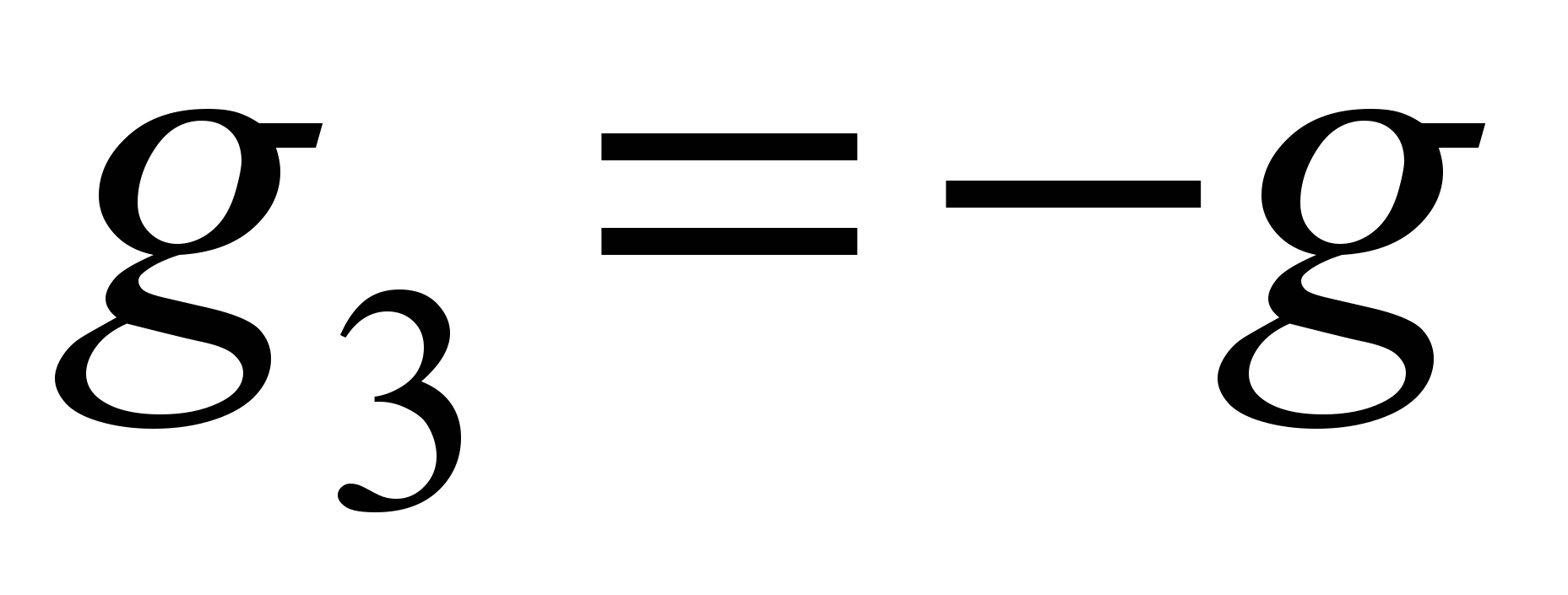, а 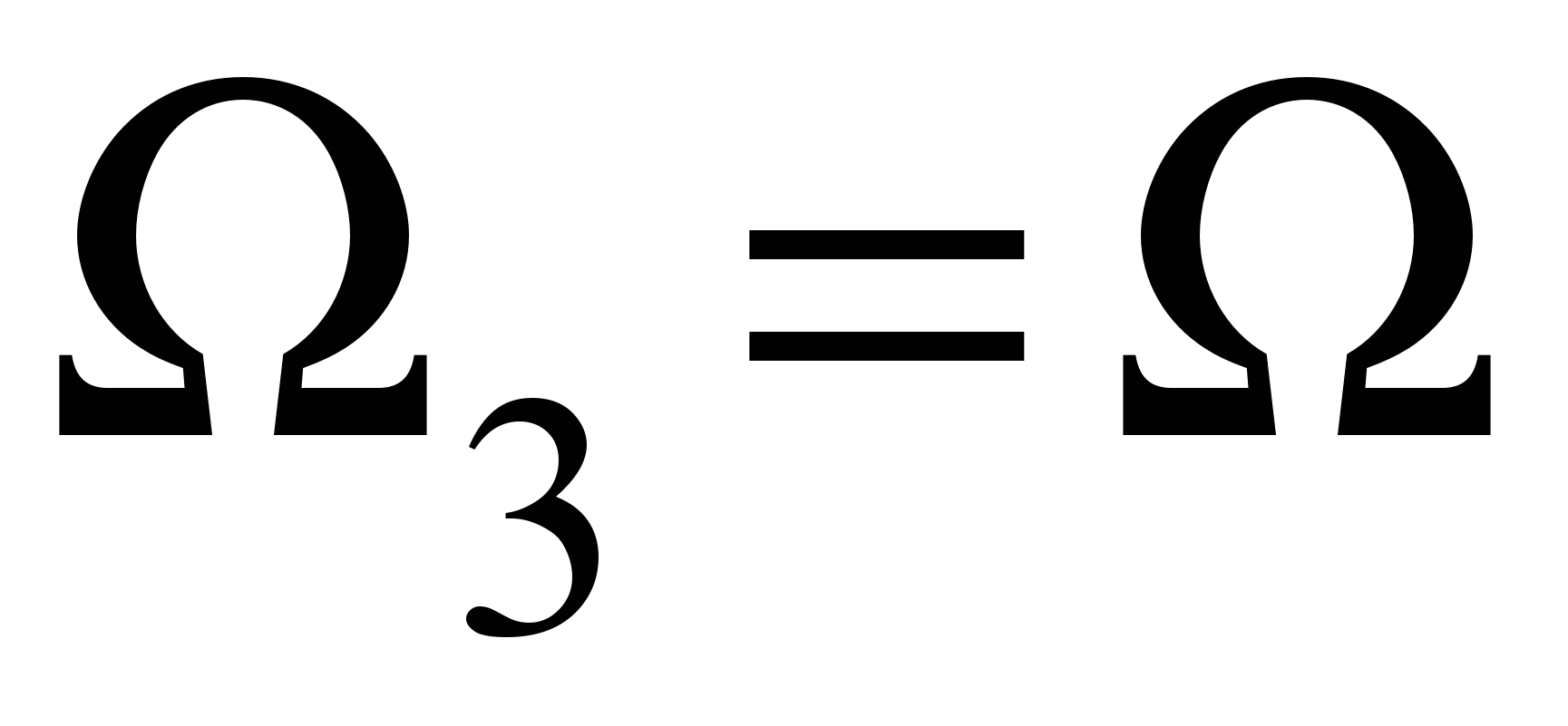(-угловая скорость относительно вертикальной оси, 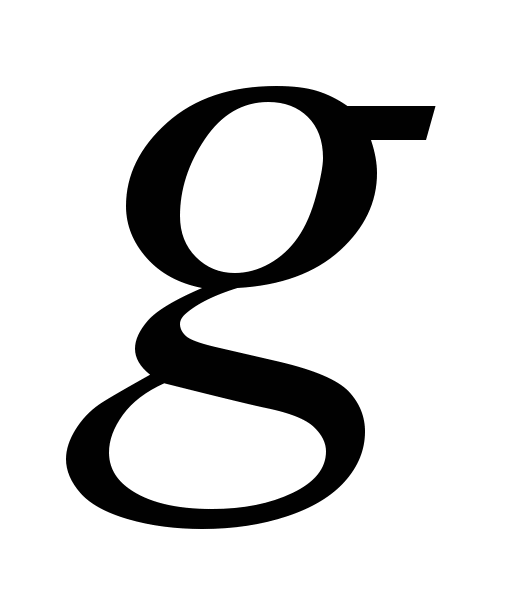-ускорение свободного падения). Уравнение (1) в данном случае приводится к виду:

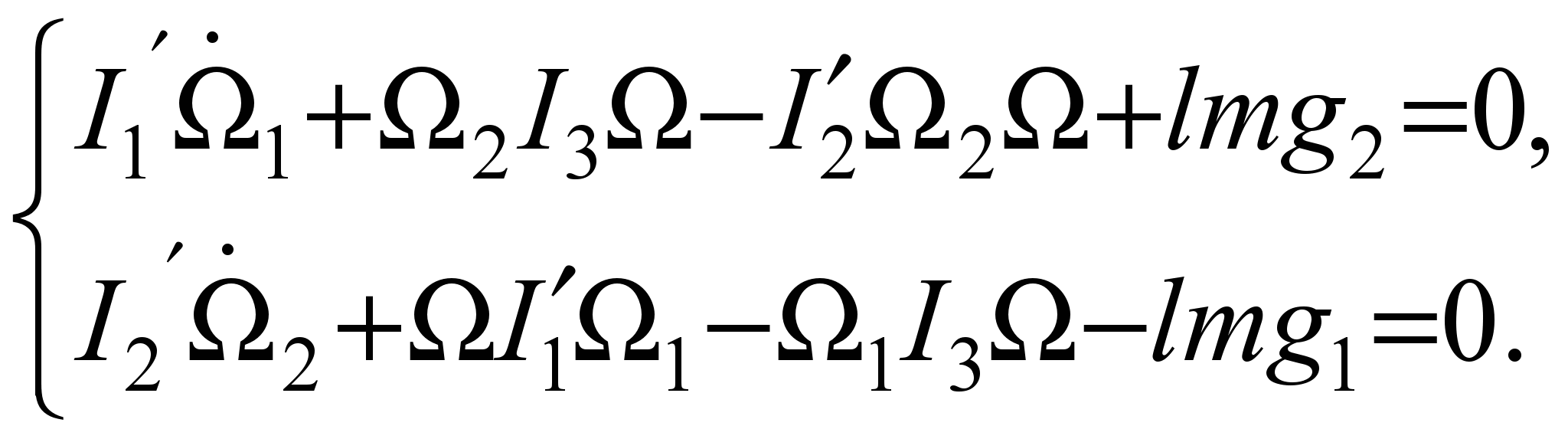(2)

Уравнение для компонент вектора ускорения свободного падения в подвижной системе координат имеет вид: 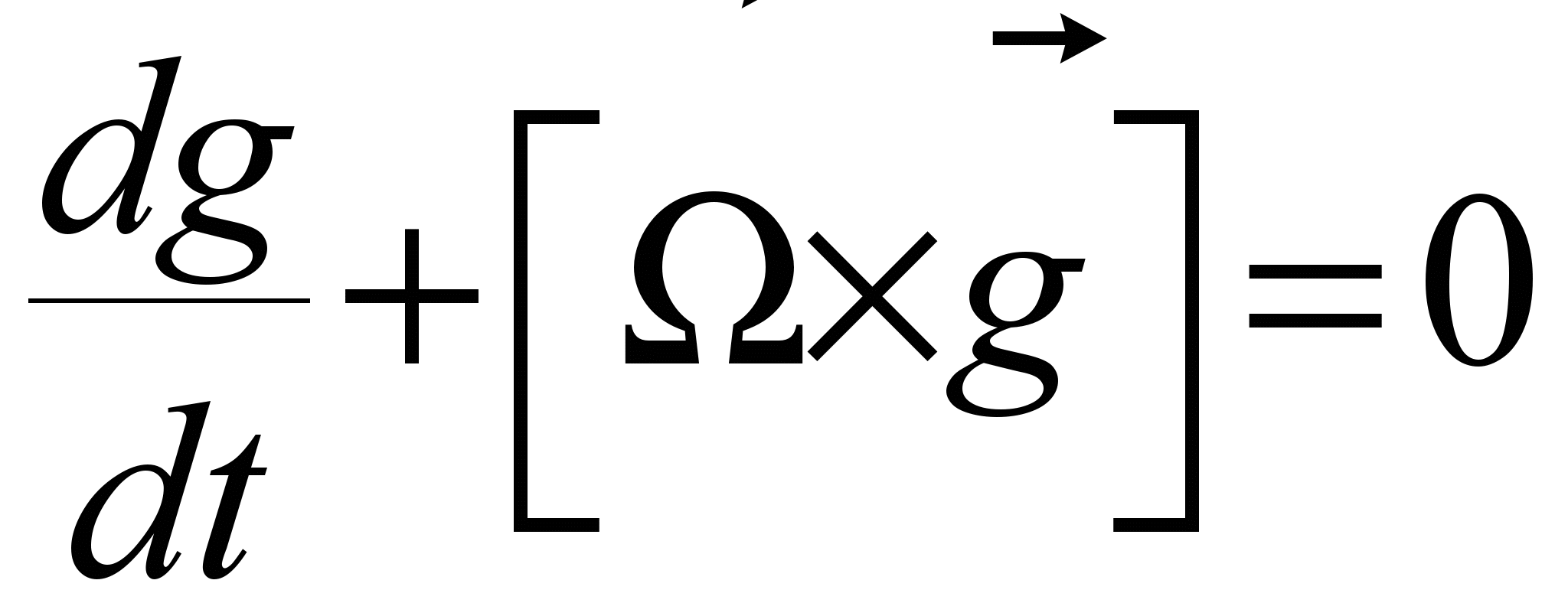, или в покомпонентной росписи:

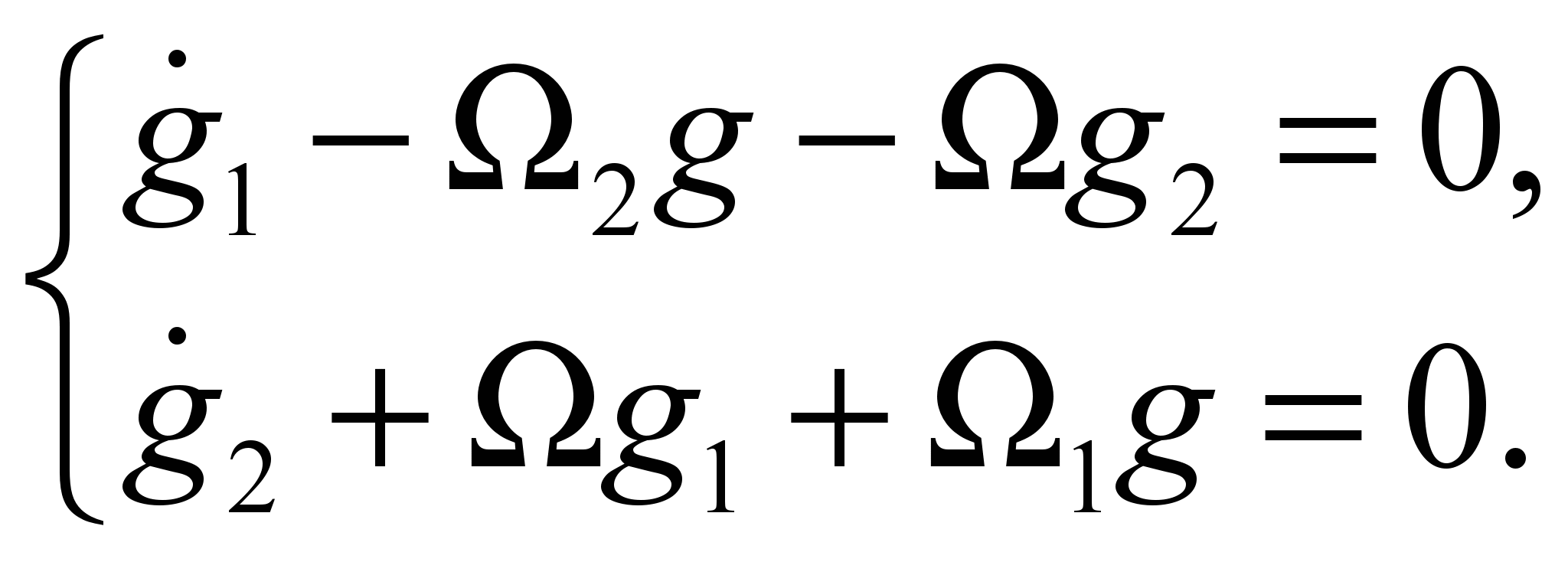(3)

В итоге мы получили систему из 4-х линейных дифференциальных уравнений 1-го порядка относительно компонент 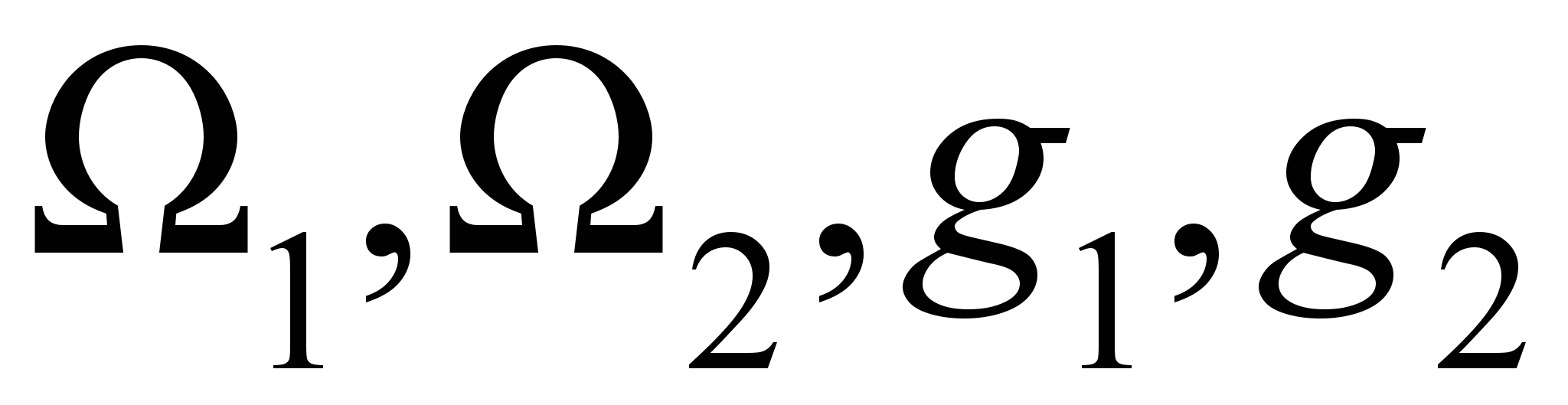, решение которой ищем в виде:

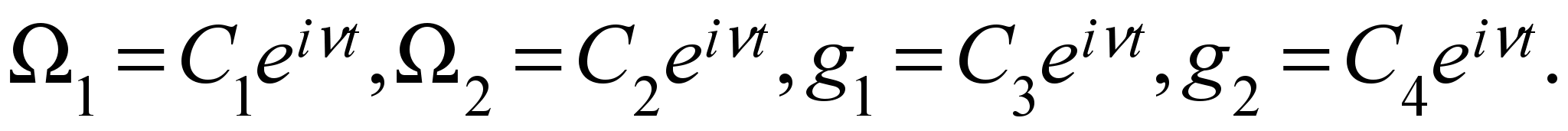(4)

Устойчивость вращения соответствует вещественным значениям частоты 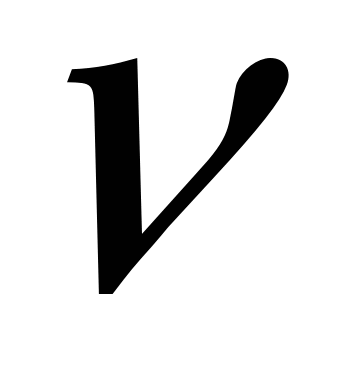. Подставив (4) в систему уравнений (2,3), получим систему линейных, однородных уравнений относительно коэффициентов 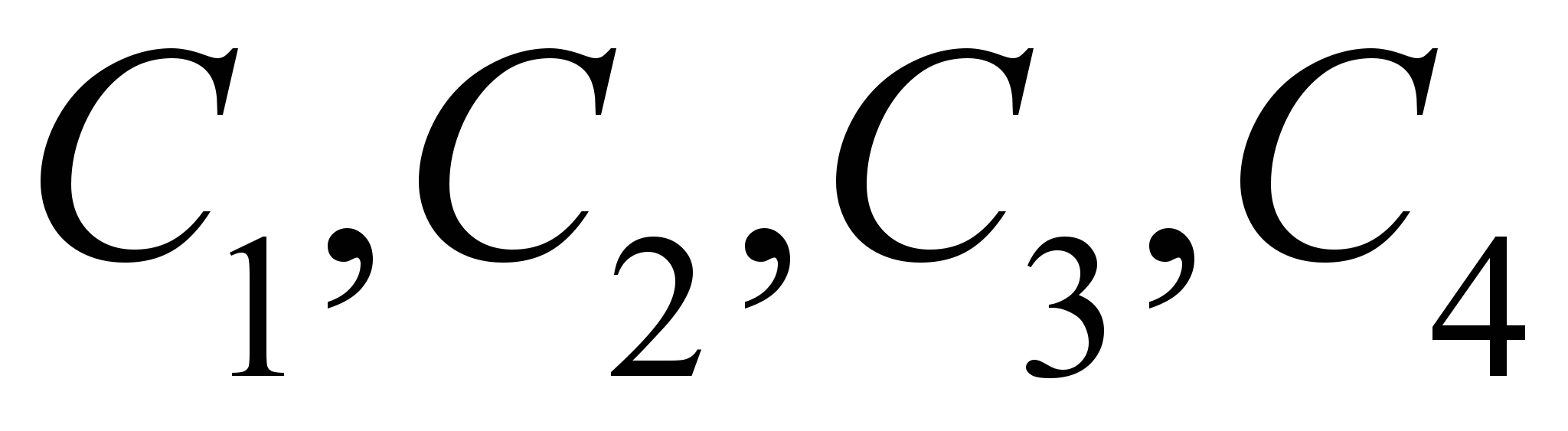. Система имеет решения, если её дискриминант 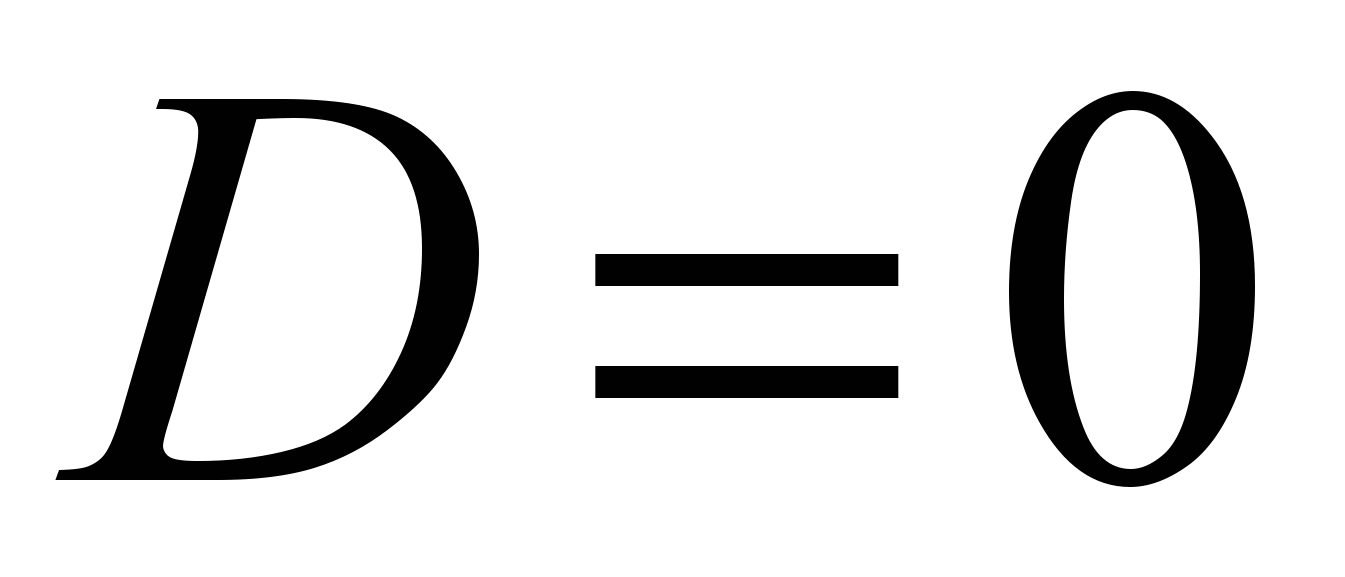. Последнее уравнение является биквадратным относительно величины ν.

Исследуемый волчок представляет собой эллипсоидальную тонкую пластину с полуосями =2 и 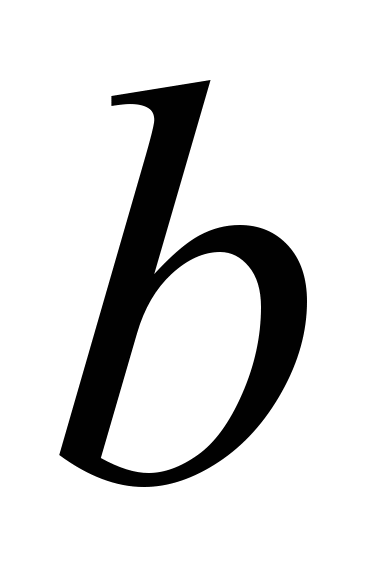=1, невесомая вертикальная ось перпендикулярна пластине и проходит через её центр, 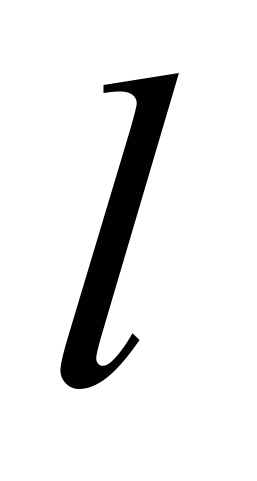-расстояние от пластины до нижней неподвижной точки, которое может изменяться в диапазоне значений от 0.1 до 1.5.

Ниже приведен график зависимости величины ν2 относительно квадрата угловой скорости вращения волчка для случая 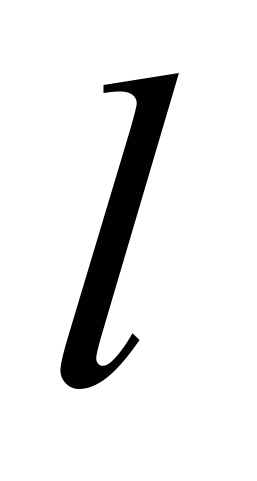=0.9.

Устойчивому вращению волчка соответствует вещественный диапазон частот 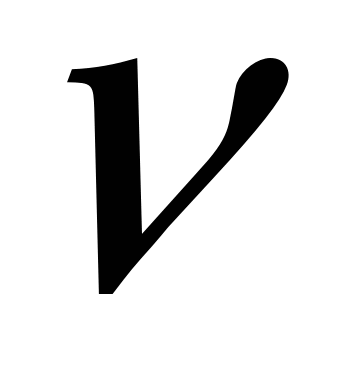, т.е. положительные значения 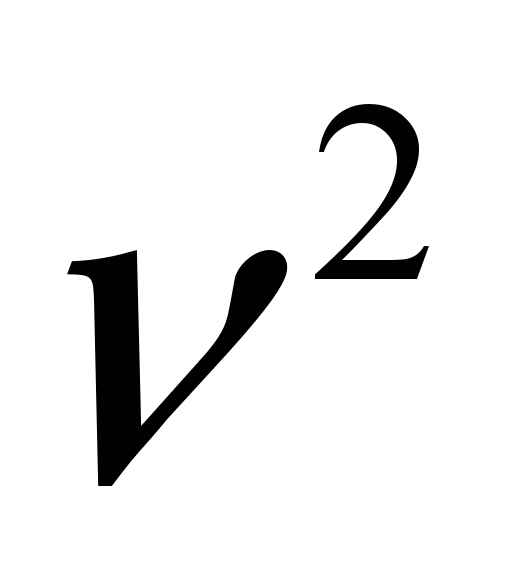. Из рисунка видно, что существует область значений угловых скоростей, при которых вращения волчка устойчиво. Указанная область лежит между точкой ветвления решения уравнения 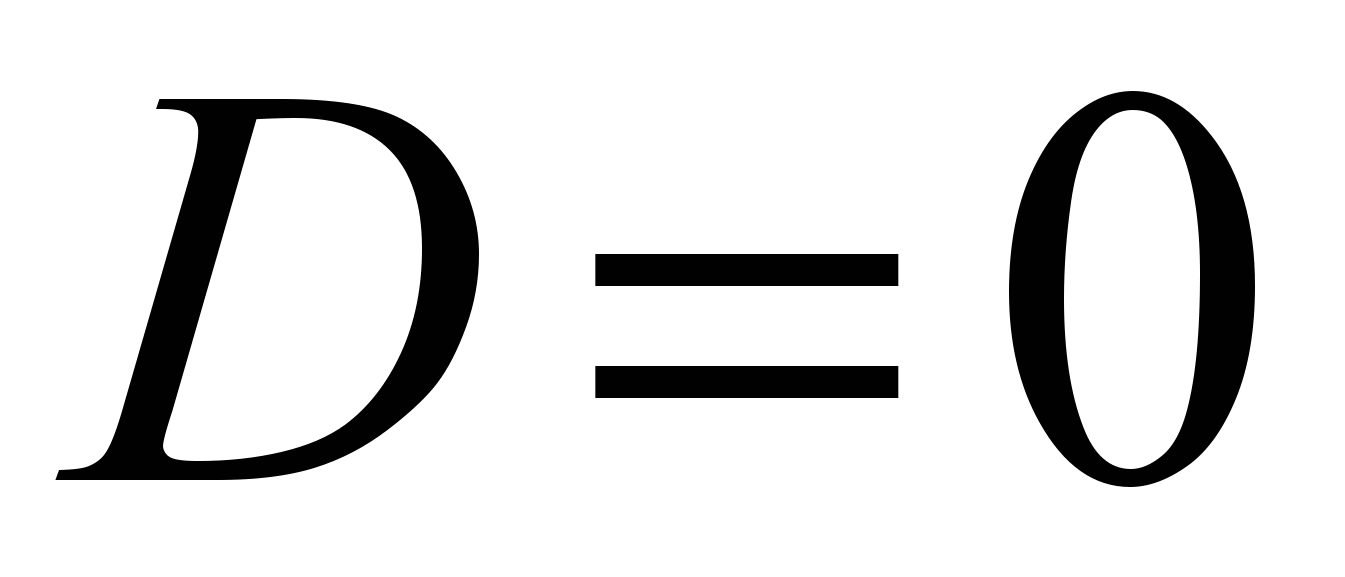и точкой пересечения величины 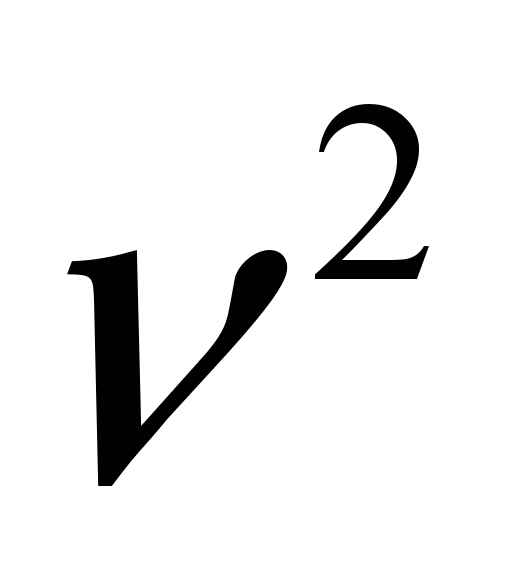с осью абсцисс данного графика.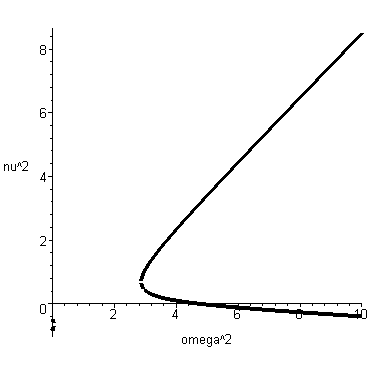




В работе проведено исследование существования областей частот устойчивого вращения волка при изменении величины расстояния от пластины до нижней точки 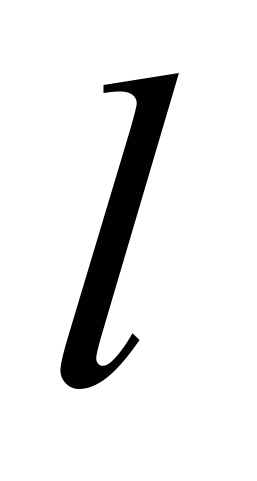в указанном выше диапазоне значений. На следующем графике приведены результаты данного исследования. На оси абсцисс отложены значения величины 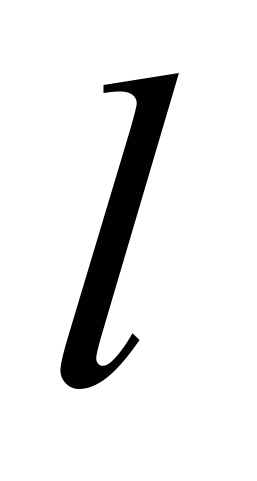, а на оси ординат значения величины угловой скорости вращения волчка вокруг вертикальной оси.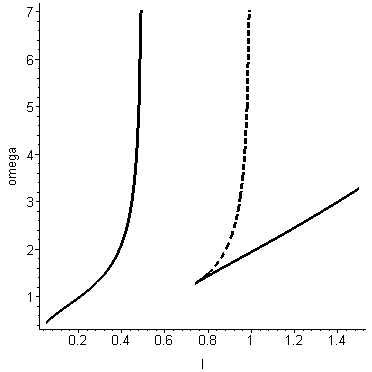




Сплошная линия соответствует минимальному значению, пунктирная – максимальному значению угловой скорости устойчивого вращения волчка с фиксированным значением величины .

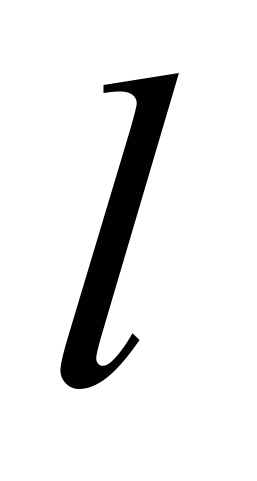При значениях 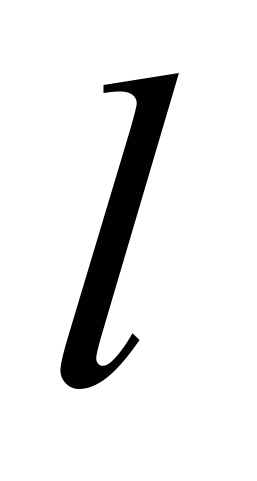<0.5 вращение тяжелого асимметрического волчка с неподвижной нижней точкой устойчиво, если значение угловой скорости больше критического значения. При значениях 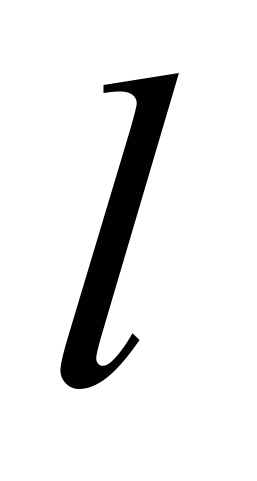, лежащих в диапазоне от 0.5 до 0.77 вращение неустойчиво при любых значениях . При значениях 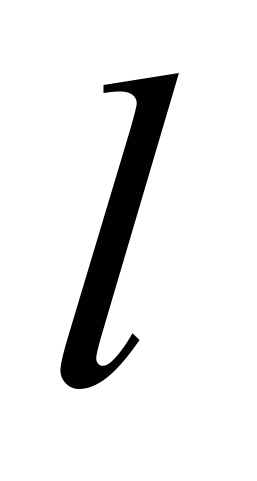в диапазоне от 0.77 до 1.0 существует полоса значений угловых скоростей устойчивого вращения. При значениях 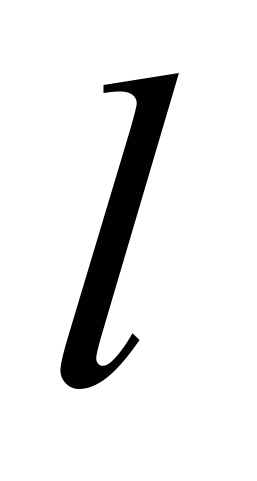>1.0 вращение устойчиво, если значение угловой скорости больше критического значения

Литература

[1] Л.Д. Ландау, Е.М. Лифшиц. Механика. М.:Наука, 1988г.