Geum.ru

Министерство образования и науки Российской Федерации Ростовский Государственный Университет

Вид материалаДокументы

Содержание


ЭЛЕКТРОННЫЙ УЧЕБНИК «ОСНОВЫ ТЕОРИИ КОДИРОВАНИЯ» Попов А.П., Барышникова Н.А.
Подобный материал:
1   ...   45   46   47   48   49   50   51   52   ...   75


ЭЛЕКТРОННЫЙ УЧЕБНИК «ОСНОВЫ ТЕОРИИ КОДИРОВАНИЯ»

Попов А.П., Барышникова Н.А.

Ростовский государственный педагогический университет




Электронный учебник «Основы теории кодирования» создан на базе спецкурса «Основы теории информации и кодирования» для студентов четвертого курса отделения информатики РГПУ.

Необходимость создания подобного учебника вызвана тем, что работы основоположников теории информации и кодирования, в которых задачи и методы теории излагаются систематически, давно не переиздавались и стали труднодоступными. В современных же учебных пособиях многие вопросы теории кодирования излагаются слишком кратко и, иногда, поверхностно, так что учащемуся, не знающего предшествующих этапов развития теории, трудно составить правильное представление о происхождении основных идей теории кодирования и методах решения типичных прикладных задач.

Естественно, что учебник по теории кодирования, в создании и развитии которой участвовали выдающиеся математики и крупные специалисты по теории связи, не может не быть компилятивным. Но и в этих условиях можно изложение даже традиционных вопросов сделать доступным, интересным и в какой-то мере увлекательным. Мы пытались достичь этого за счет большого числа примеров, иллюстрирующих то или иное положение теории, а также решая на практических занятиях достаточно сложных задач, тесно связанных с материалом лекционного курса.

Так, при изучении темы «Оптимальные коды» не только дается описание алгоритма Хаффмена, но и на конкретном примере подробно разбирается прямой и обратный ход алгоритма (ниже приводится соответствующий фрагмент текста учебника).

Прямой ход алгоритма Хаффмена. Выполняемая на каждом шаге прямого хода алгоритма Хаффмена операция сжатия заключается в том, что два наименее вероятных символа алфавита сжимаются в один, при этом их вероятности суммируются. Таким образом, на каждом шаге происходит редукция алфавита, в результате чего он заменяется новым алфавитом с количеством символов на 1 меньше. Прямой ход алгоритма заканчивается, когда на очередном шаге все символы исходного алфавита объединятся в один символ последнего редуцированного алфавита.


a
b
c
d
e
f
g

0.26
0.21
0.20
0.11
0.10
0.06
0.06

a
b
c
fg
d
e



0.26
0.21
0.20
0.12
0.11
0.10



a
b
de
c
fg






0.26
0.21
0.21
0.20
0.12






cfg
a
b
de









0.32
0.26
0.21
0.21









bde
cfg
a












0.42
0.32
0.26












acfg
bde















0.58
0.42















acfgbde


















1



















Обратный ход алгоритма Хаффмена. В процессе выполнения обратного хода алгоритма Хаффмена последовательно строятся оптимальные кодировки для всех промежуточных редуцированных алфавитов. Единственному символу самого последнего из редуцированных алфавитов ставится в соответствие пустой код. Операция расщепления, которая выполняется на каждом шаге обратного хода алгоритма Хаффмена, является обратной к соответствующей операции сжатия: соединенные ранее вместе символы очередного редуцированного алфавита вновь расщепляются на составляющие их компоненты – символы алфавита-предшественника. При этом происходит назначение очередного кодового символа: одной из компонент назначается нуль, а другой компоненте единица.

a
b
c
d
e
f
g

01
10
000
110
111
0010
0011

a
b
c
fg
d
e



01
10
000
001
110
111



a
b
de
c
fg






01
10
11
000
001






cfg
a
b
de









00
01
10
11









bde
cfg
a












1
00
01












acfg
bde















0
1















acfgbde


















λ



















Окончательный результат применения алгоритма Хаффмена представим в виде кодовой таблицы с указанием длин назначенных элементарных кодов.


a
b
c
d
e
f
g

0.26
0.21
0.20
0.11
0.10
0.06
0.06

01
10
000
110
111
0010
0011

2
2
3
3
3
4
4


Вычислим цену кодирования двоичного кода, найденного по алгоритму Хаффмена:

.

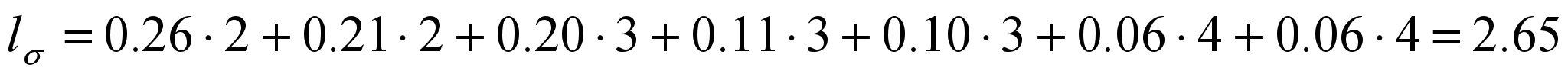На практических занятиях учащиеся получают самостоятельные задания, позволяющие окончательно закрепить приобретенные теоретические знания.

Весь материал в электронном учебнике организован с помощью системы гиперссылок. Учебник дополнен глоссарием, разъясняющим вновь вводимые термины и понятия (выделяются курсивом в основном тексте). В целом учебник оформлен средствами Dream Weaver и оформлен в виде Web-cite, который может быть размещен в локальной сети учебного заведения. заведения.