Академия управления мвд россии
| Вид материала | Учебник |
- Темы контрольных работ Аппараты мвд, ГУ мвд, У мвд, ут мвд россии по Федеральным округам, 48.32kb.
- Положение о Штабе Главного управления мвд россии по Ростовской области общие положения, 212.4kb.
- Методические рекомендации по подготовке рефератов сотрудниками подразделений уголовного, 335.13kb.
- Нижегородская академия, 209.52kb.
- Функция прогнозирования миграционных процессов в системе управления мвд россии, 462.3kb.
- Нижегородская академия, 238.9kb.
- Нижегородская академия, 214.37kb.
- Ения, подразделениях Государственной противопожарной службы мвд россии, Первом управлении, 1898.24kb.
- Инструкция по организации учебного процесса в центре профессиональной подготовки территориального, 515.25kb.
- Рабочая программа дисциплины методы исследований в менеджменте направление подготовки, 262.36kb.
Таблица 3.8.2 Результаты выборки
14*
| 16 | 22 | 20 | 19 | 18 | 24 | 21 | 17 | 23 | 18 | 19 | 16 | 22 | 18 | 23 |
| 20 | 19 | 20 | 18 | 21 | 18 | 19 | 24 | 17 | 16 | 23 | 19 | 25 | 21 | 20 |
| 18 | 19 | 22 | 20 | 18 | 17 | 21 | 19 | 20 | 23 | 25 | 22 | 20 | 17 | 24 |
| 19 | 17 | 21 | 18 | 19 | 21 | 26 | 22 | 19 | 20 | | | | | |
419
Пусть Xi наблюдался mi раз, X; - m; раз и т.д. Число наблюдений называют частотой и обозначают т. Сумма частот равна объему выборки п. Отношение частоты к объему выборки называется частостью и обозначается р;* = т;/п. Частость характеризует долю каждого значения в общем числе наблюдений и является статистической вероятностью. Варианты и соответствующие им частоты (или частости) образуют статистический ряд выборки.
Проранжируем в Excel 5.0 варианты (для этого они должны быть в одной строке или столбце) и определим с помощью «Мастера функций» частоты, соответствующие каждому варианту. В результате в рабочем листе Excel 5.0 имеем табл. 3.8.3.
Статистический ряд выборки
Таблица 3.8.3
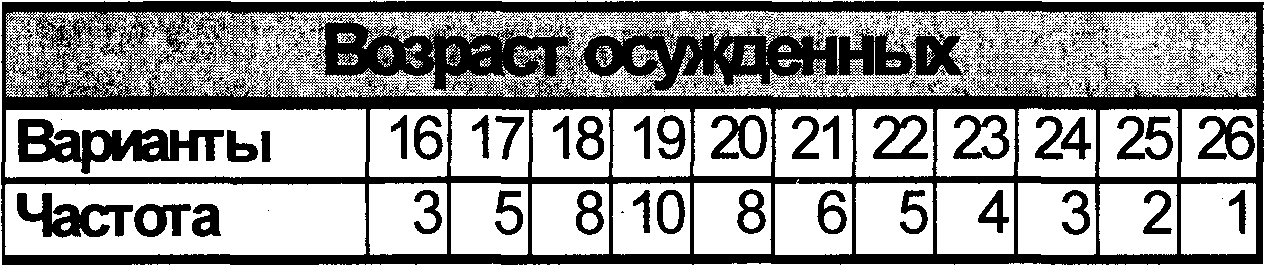
Вариационные ряды делятся на дискретные и интервальные. В дискретном ряду вариант принимает дискретное значение (количество лет, стаж работы в органах внутренних дел и др.). В случае интервального ряда значения варианта даются в виде интервалов, которые получаются в результате группировки данных наблюдения. Частоты при этом относятся не к отдельному значению признака, а к некоторому интервалу (например, варианты норм выработки в исправительных учреждениях в виде интервалов: 65-70%, 70-75%, 80-85% и т.д.).
Статистический ряд является эмпирическим законом распределения выборочной совокупности. К универсальной характеристике случайной величины относится ее функция, или плотность, распределения. Функцию распределения генеральной совокупности будем называть теоретической функцией распределения F(x), а статистическую функцию распределения выборки - эмпирической функцией распределения Fn (x).
При больших объемах наблюдений n Fn (x) —> F(x), т. е. эмпирическая функция распределения выборки с ростом ее объема приближается к теоретической функции распределения генеральной сово-
420
купности и может быть использована для ее приближенного представления.
Для достижения наглядности строят различные графики статистического распределения, из которых чаще всего используют полигон или гистограмму. Они являются графическим изображением статистического ряда. Графики, подобно другим искусственным языкам, (например, математическому) имеют целый ряд положительных свойств, особенно в смысле лаконичности, однозначности и наглядности.
Выделив табл. 3.8.2 в рабочем листе Excel 5.0 для Windows, можно построить гистограмму, полигон и кумулятивную кривую (кумуляту). За это отвечает «Мастер диаграмм».
При построении гистограммы над каждым временным интервалом (в один год) варианта строится прямоугольник, высота которого пропорциональна соответствующей частости, выраженной в % (см. рис. 3.8.1).
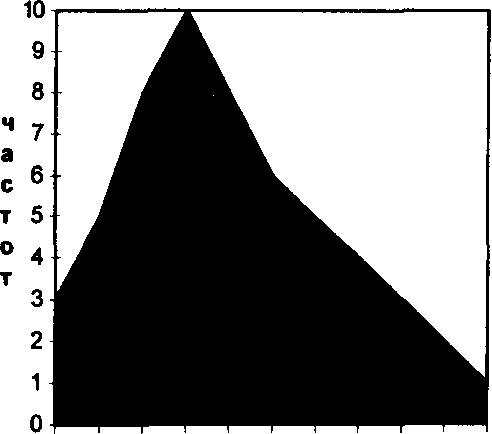
Полигон строят из отрезков, соединяющих точки, координатами которых являются значения вариантов X, и соответствующие частости, или частоты. На рис. 3.8.2 в виде полигона отображен вариационный ряд из табл. 3.8.3.
На оси ординат отложены частоты ряда. Из гистограммы можно получить полигон распределения, для чего необходимо соединить ломаной линией середины верхних сторон прямоугольников. При увеличении объема выборки число сторон полигона распределения будет расти, и его ломаная линия будет стремиться к плавной кривой распределения, которая отражает теоретическое распределение генеральной совокупности.
В ряде случаев для изображения вариационного ряда используется кумулятивная кривая (см. рис. 3.8.3). Для ее построения подсчитываются по вариантам накопленные частоты, или частости. Первому варианту Xi (16 лет) соответствует частость mi/n, второму X; - сумма (mi + mz)/n, третьему X - сумма (mi+ т-+ гпз)/п и т.д. Последнему варианту Хщах соответствует накопленная частость, равная единице или 100, если подсчет ведется в %.
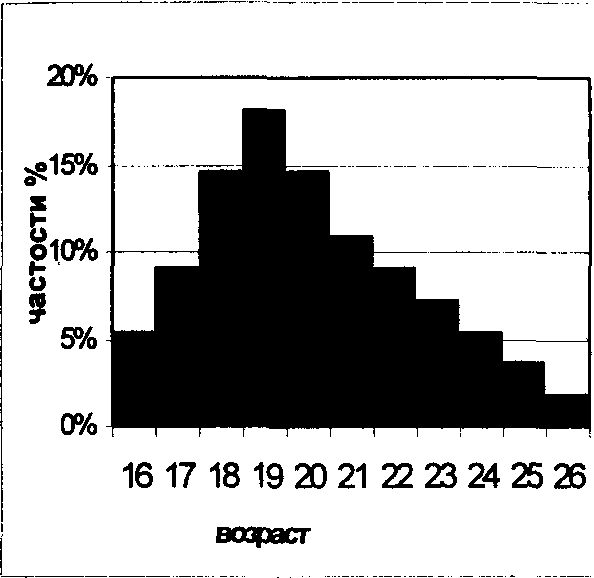
Рис. 3.8.1. Гистограмма
421
• В 17 18 19 23 21 22 23 24 25 26 возраст
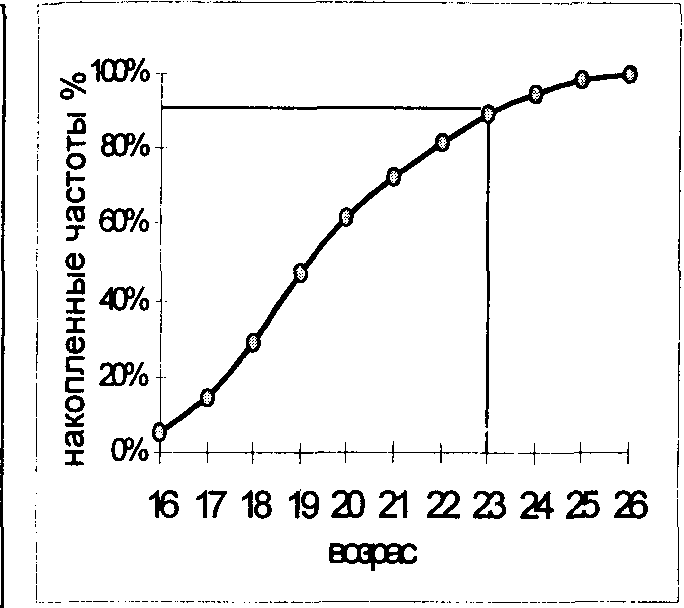
Рис. 3.8.2. Полигон
Рис. 3.8.3. Кумулята
Накопленные частоты показывают, сколько единиц совокупности имеют значения признака не больше, чем рассматриваемое значение. Так, на рис. 3.8.3 показано, что возраст 90% осужденных за совершение тяжких телесных повреждений не превышает 23 лет.
Иногда в статистике, помимо диаграмм, применяется еще особый вид графических изображений вариантов - картограммы. Картограмма - это изображение величины интересующего признака (его размещение, интенсивность) на географической карте с помощью графических символов: штриховки, расцветки,» точек. Картограмма иллюстрирует содержание статистических таблиц, подлежащим которых является административно-географическое деление совокупности. Разновидностью картограммы является картодиаграмма. Она представляет собой географическую карту, по отдельным районам или пунктам которой размещены графические знаки (столбики, круги и т.д.), соответствующие величине статистических показателей, изображенных на ней. Следует отметить, что Excel 7.0 способен создавать картодиаграммы.
Варианты статистического ряда могут быть абсолютными и относительными величинами. Абсолютные величины - форма выражения статистических показателей, непосредственно характеризующая абсолютные размеры правовых явлений, их признаков в единицах соответствующих систем измерения. Так, абсолютные величины характеризуют общее количество зарегистрированных преступлений, общую сумму ущерба, сроки лишения свободы, число уголовных дел и др.
422
Однако сравнительный анализ преступности по отдельным регионам нельзя проводить путем использования абсолютных величин, поскольку регионы могут отличаться по численности населения и другим параметрам. Поэтому для сравнения, обобщения, определения интенсивности развития исследуемого явления, его структуры, динамики используются относительные величины.
Относительные величины - это отношение двух величин. Числитель отношения - текущие данные об исследуемом явлении (преступления, суммы ущерба и т.д.). Знаменатель отношения называется основанием или базой (сравнения). В качестве текущей или базисной могут выступать как одноименные, так и разноименные величины. В первом случае получаем безразмерные величины. Если основание принять за единицу, то величины образуют долю, или коэффициент. Он показывает, во сколько раз сравниваемая величина больше или меньше основания, например доля квартирных краж в преступлениях по линии уголовного розыска. Если основание принять за 100%, то относительная величина будет выражаться в процентах (например, число преступлений в регионе в 1998 г. - 2930, в 1997 г. - 2014, темп роста преступности К = 2930/2014*100= 145,5%). К разноименным относительным величинам относятся, например, уровень преступности в расчете на 10 тыс. человек, нагрузка на одного следователя и др.
Средние и относительные величины относятся к обобщающим показателям, которые характеризуют одним числом типичные, наиболее распространенные стороны изучаемых явлений. Обобщающие показатели отражают по определенному признаку всю совокупность в целом, отвлекаясь от частного и случайного, что дает возможность установить и измерить закономерности различных массовых процессов.
Главное значение средних величин состоит в замене множества различных индивидуальных значений признака средней величиной, характеризующей всю однородную совокупность. В статистике к средним величинам относятся: средняя арифметическая, средневзвешенная, .средняя геометрическая, средняя гармоническая, средняя квадратическая, средняя кубическая, медиана, мода. Рассмотрим некоторые из них.
Средняя арифметическая величина получается путем деления суммы величин вариантов на их число. При ее вычислении общий объем признака мысленно распределяется поровну между всеми единицами совокупности. В результате получается средняя арифметическая величина - среднее слагаемое. Формула средней арифметической имеет следующий вид:
423
x = x i + x 2 +•••+ x
Z x
(3.8.2)
X - средняя величина; n - численность совокупности.
Если же отдельные значения признака повторяются неодинаковое число раз, то средняя определяется по формуле средней взвешенной арифметической. Формула имеет вид:
Sx,*f,
if,
(3.8.3)
где fi - значение частот; i - номер интервала с одинаковыми вариантами; k - число интервалов.
Частоты нередко называют весами средней, отсюда и происходит название средней взвешенной.
В теории вероятностей такую же формулу имеет показатель -математическое ожидание. Его формула имеет вид:
£x,*
М(х)=
(3.8.4)
где М(х) - математическое ожидание; р, - вероятность появления значения х; случайной величины X.
Математическое ожидание представляет собой центр распределения, около которого сосредоточены все возможные значения случайной величины. Поэтому математическое ожидание иногда называют просто средним значением случайной величины.
Для определения средних темпов прироста или снижения признака (например, количества преступлений), когда на протяжении всех исследуемых лет происходит либо его непрерывный рост, либо непрерывное снижение, применяется средняя геометрическая, которая определяется по формуле:
K.eoM-k,*k2*...*kn ,
где k; - темп роста в i-й период; n - число периодов.
(3.8.5)
424
В качестве примера рассмотрим число уголовных дел на одного следователя по годам (см. табл. 3.8.4).
Таблица 3.8.4 Динамика нагрузки на следователя по годам
| Показатель | Годы | |||
| 1 | 2 | 3 | 4 | |
| Число дел на одного следователя | 20 | 24 | 36 | 72 |
Обозначим нагрузку на следователя как X. Тогда ki=X2/Xi=24/20 = 1,2; k2=Xa/X2 =36/24= 1,5; k3=X4/X3=72/36= 2.
______ Следовательно, за четыре года число
{ =/1,2*1,5*2 =1,5 дел на одного следователя в среднем увеличивалось в 1,5 раза. Используя этот показатель, можно осуществить прогноз на пятый год при условии сохранения тенденции. Для этого нужно нагрузку на следователя в четвертом году умножить на среднее геометрическое, т.е. Х5 = Х4* 1.5=72* 1.5=108 уголовных дел.
Отметим, что все интересующие исследователя показатели, характеризующие вариационный ряд, без труда можно проводить в табличном процессоре Excel 5.0 для Windows. Его пользователю не нужно знать математических формул, достаточно обратиться к «Мастеру функций» и он проведет все расчеты.
Для вариационного ряда, представленного в табл. 3.8.3, расчетные показатели, полученные Excel 5.0, приведены в табл. 3.8.5. Так, средневзвешенная величина равна 20,05, а средняя геометрическая равна 19,9. Здесь средняя геометрическая рассчитывает не темп роста, а качественное удаление от максимального и минимального значений с учетом частот вариантов.
При изучении вариационного ряда применяются также характеристики, которые описывают его структуру, строение. К ним относятся медиана и мода.
Медиана (обозначается «Me») - значение величины вариационного ряда, расположенного в его середине, т.е. она делит ряд на две равные части. Медиана в отличие от средней не зависит от значений признака, стоящих на краях вариационного ряда
425
(перед вычислением медианы ряд должен быть обязательно ранжирован, если до этого он не подвергался сортировке).
Если в вариационном Таблица 3.8.5
Расчет показателей ряда приложением Excel
| ПОКАЗАТЕЛИ | |
| Средняя величина | 20,05 |
| Медиана | 20 |
| Мода | 19 |
| Средняя геометрическая | 19,9 |
| Средняя гармоническая | 19,8 |
| Максимум | 26 |
| Минимум | 16 |
| Размах вариации | 10 |
| Среднее линейное отклонение | 1,99 |
| Дисперсия | 6,13 |
| Среднее квадратическое отклонение | 2,48 |
| Коэффициент вариации | 0,12 |
| Скос | 0,45 |
| Эксцесс | -0,44 |
ряду четное число вариантов, то Me будет половиной суммы двух серединных вариантов. На практике медиана применяется в качестве средней в случае больших колебаний в значениях варьирующего признака.
Модой (обозначается Мо) называется вариант признака, имеющий наибольшую частоту, т. е. мода - наиболее типичное значение признака. Из табл. 3.8.5 видно, что Мо = 19, Me = 20. Как правило, в вариационных рядах Мо < Me Хсредн. Если они равны друг другу, то вариационный ряд подчиняется нормальному закону распределения. В случае различия их значений эти показатели используются для характеристики асимметрии (скоса) кривой распределения. В нашем случае (см. табл. 3.8.5) они близки друг другу (19; 20; 20,05), поэтому можно предположить, что эмпирический ряд близок к нормальному закону распределения.
Однако для характеристики исследуемого признака совокупности недостаточно иметь данные о средней величине этого признака. Бывают такие случаи, когда средние величины двух и более совокуп-ностей одинаковые, но они существенно отличаются своей вариацией, т.е. в одной совокупности отдельные варианты могут далеко отстоять от средней, а в другой - они могут размещаться кучно возле средней.
Если отдельные варианты недалеко отстоят от средней, данная средняя хорошо представляет свою совокупность. Для того чтобы изучить, как велики эти отклонения, их измеряют при помощи ряда показателей вариации.
426
Для характеристики величины колебания в статистике исчисляют следующие показатели: размах вариации; среднее линейное отклонение; дисперсия; среднее квадратическое отклонение; коэффициент вариации.
Размах вариации является наиболее простым измерителем вариации и представляет собой разность между наибольшим и наименьшим значениями признака. Его формула имеет вид:
R = X щах- Х mm , (3.8.6)
где Х щах - наибольшее значение признака; Х щ,п - наименьшее значение признака.
В нашем случае R = 10 (см. табл. 3.8.5). Поскольку величина размаха характеризует лишь максимальное различие значений признака, она не может измерять закономерную силу его вариации во всей совокупности.
Более точную характеристику колеблемости можно получить, если сравнить все имеющиеся значения с их средней величиной. Также сравнение можно сделать на основе среднего линейного отклонения, которое от среднего значения отнимает значения вариантов по абсолютной величине (не учитывая минусов). Его формула имеет вид:
а=
п
£
Xi-X|
(3.8.7) или с учетом частот (3-8-8)
k
Zx,
а=
*
n
n
j - номер интервала с одинаковыми частотами.
Для выборочной совокупности, представленной в табл. 3.8.3, а =1,99 (см. табл. 3.8.5).
Простота расчета и интерпретации составляет положительные стороны данного показателя, однако его нельзя поставить в соответствие с каким-либо вероятностным законом, в том числе и с нормальным распределением, одним из параметров которого является среднее квадратическое отклонение.
В математической статистике для оценки рассеяния вариантов используется дисперсия (Д), часто называемая средним квадратом отклонения. Ее формула имеет следующий вид:
n __ k ——2 .
£(Xi-X) (3.8.9) или с учетом E(Xj-X) * fj D=ст2=м————— частот (3.8.10) 0=————————
П
n
427
Для нашего вариационного ряда D = 6,13 (см. табл. 3.8.5). На использовании дисперсии основаны практически все методы математической статистики. Однако в ряде случаев D неудобно пользоваться, так как она имеет размерность X2.
Значительно более употребимой характеристикой колеблемости признака в изучаемой совокупности является среднее квадратическое отклонение, размерность которого совпадает с размерностью вариантов вариационного ряда. Его величина определяется как квадратный корень из дисперсии, а именно:
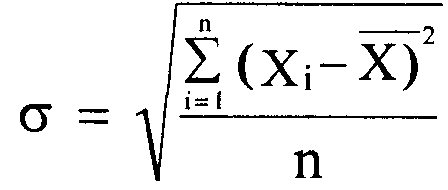
(3.8.11) или с учетом частот (3.8.12)
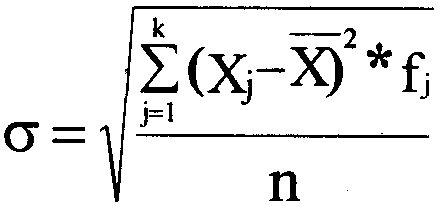
Среднее квадратическое отклонение в реальных совокупно-стях всегда больше среднего линейного отклонения. Соотношение ст/а зависит от наличия в совокупности резких выделяющихся отклонений и может служить индикатором «засоренности» совокупности неоднородными с основной массой элементами. Чем это соотношение больше, тем сильнее подобная «засоренность». Для нормального закона распределения ст/а = 1,25. Для нашего вариационного ряда ет/а =2,48/1,99 = 1,25, что говорит об его хорошей близости к нормальному закону распределения.
Для оценки интенсивности вариации и для сравнения ее в разных совокупностях и тем более для разных признаков используются относительные коэффициенты вариации. Чаще других применяется коэффициент вариации, являющийся отношением среднего квадрати-ческого отклонения к среднему значению математического ожидания вариационного ряда. Его формула имеет вид: V = ст/М (3.8.13). Для нашего случая V= 0,12 (см. табл. 3.8.5). Коэффициент вариации часто используют самостоятельно для определения степени согласованности экспертов при их оценке различных объектов. Чем меньше V и ближе к нулю, тем мнения экспертов считаются более согласованными.
Иногда подсчитывают показатель репрезентативности (имеет формулу qOO0//!!) вариационного ряда. Он не должен превышать 5%. Для нашего случая q = 1,62%.
Для дальнейшего изучения характера вариации используются такие показатели, как скос (коэффициент асимметрии), эксцесс.
428
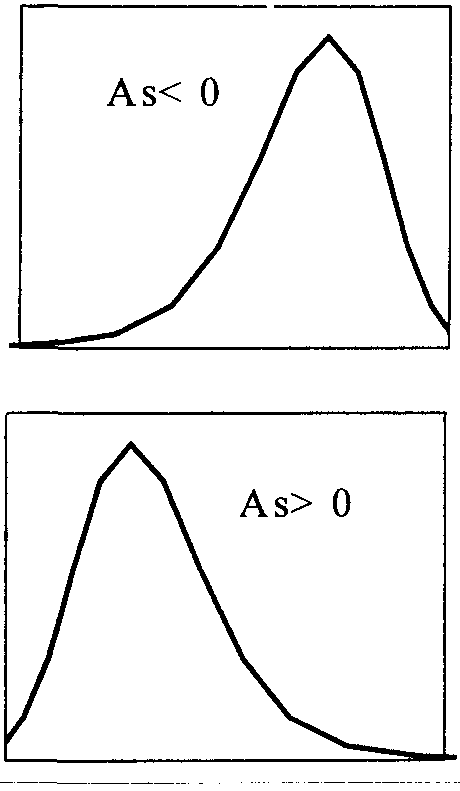
Рис. 3.8.4. Виды асимметрии
Скос (коэффициент асимметрии, обозначается «As» показывает, какая из ветвей кривой распределения длиннее другой. Если As <0, левая ветвь длиннее правой, т.е. имеем левостороннюю асимметрию (см. рис.3.8.4). Если As>0, правая ветвь длиннее левой, что свидетельствует о правосторонней асимметрии (см. рис. 3.8.4). Из рисунка 3.8.2 видно, что полигон вариационного ряда скошен, при этом As = 0,45 (см. табл. 3.8.5). Налицо -незначительная правосторонняя асимметрия.
Эксцесс (обозначается «Ех») характеризует еще более сложное свойство вариационных рядов, а именно-степень крутизны распределения по сравнению с кривой нормального распределения. Кривые, у которых эксцесс отрицательный (Ех<0), имеют более плоские вершины по сравнению с нормальной кривой и называются плосковершинными.
Кривые, у которых эксцесс положительный (Ех>0), имеют более острую вершину по сравнению с нормальной кривой и называются островершинными (см. рис. 3.8.5).
Для нашего вариационного ряда Ех = -0.44 (см. табл. 3.8.5), что свидетельствует о незначительной островершинности эмпирической кривой распределения. Для нормального распределения As=Ex=0. Скос и эксцесс имеют довольно сложные математические выражения (см. формулы 3.8.13 и Рис. 3.8.5. Сравнение теоретической и экс- „ „ ,
периментальной кривых
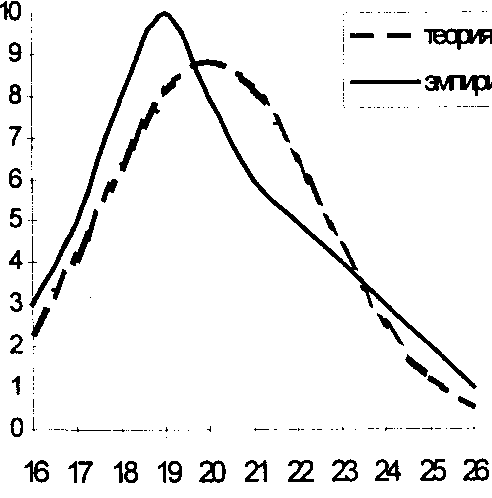
429
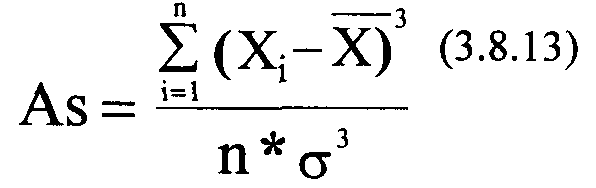
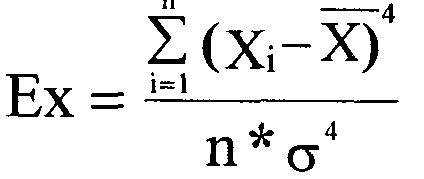
(3.8.14)
Однако, обратившись к «Мастеру функций» программного средства Excel 5.0 для Windows, пользователь оперативно подсчитает As и Ex. Отметим, что использование современных аппаратных и программных средств позволяет не только повысить оперативность подготовки представления статистической информации, но и существенно увеличить и усилить ее аналитические возможности.
Итак, анализируя средние и вариационные показатели вариационного ряда (см. табл. 3.8.2), можно сделать предположение, что его генеральная совокупность хорошо согласуется с нормальным законом распределения или, другими словами, теоретическая кривая нормального распределения хорошо описывает эмпирические данные нашего ряда.
К такому же выводу можно прийти, сравнивая близость эмпирических и теоретических кривых. Однако теоретические и эмпирические законы распределения могут значительно отличаться друг от друга. Расхождение между ними может быть случайным и объясняться малым объемом выборки, неудачным способом группировки статистических данных. Но, возможно, причина расхождения в том, что была не верна исходная посылка или, как принято говорить в статистике, гипотеза о виде теоретического закона распределения. Помимо нормального закона распределения существует и много других, например закон Пуассона, биномиальный закон распределения и др.
Если теоретическая кривая подобрана неверно, то естественно, что расхождение ее с экспериментальным распределением не случайно, а закономерно. Для того чтобы вынести суждение о том, насколько распределение теоретического и эмпирического законов распределения существенно, используется критерий согласия.
Критерием согласия называют критерий гипотезы о том, что генеральная совокупность имеет теоретическое распределение предполагаемого типа.
Статистическая гипотеза о том, что эмпирическое распределение случайной величины описывается известным теоретическим законом распределения, называется нулевой. Понятие гипотезы, с которым имеет дело математическая статистика, более узко, чем общее
430
понятие гипотезы (предвидение того, что ожидается от исследования). Статистические гипотезы касаются поведения наблюдаемых случайных величин (вариантов статистических рядов). Их проверка осуществляется путем сопоставления с результатами наблюдений. Но результаты наблюдений зависят от случая. Поэтому статистические гипотезы носят не категорический, однозначный характер, а характер правдоподобного утверждения, которое также имеет вполне определенную вероятность (р = 0,95 - 0,99).
Критерии согласия позволяют судить о том, согласуются ли наблюдавшиеся значения случайной величины с выдвинутой нулевой гипотезой о виде ее распределения. Существуют критерии согласия Колмогорова, Пирсона, Смирнова, Романовского, Ястремского и др. Наиболее часто используют для проверки критерий Пирсона, называемый также критерием у1 (хи-квадрат), который устанавливает критическую меру расхождения между теоретическим и практическим законами распределения.
Порядок проверки гипотезы о виде закона распределения с помощью критериев согласия состоит из следующих шагов.
1. Выдвигается гипотеза о виде закона распределения вариационного ряда и определяются его показатели.
2. Задают уровень значимости критерия а, например а = 0,01. Это значит, что с вероятностью р = 1 - а = 0,99 ( 99 %) гипотеза будет принята правильно.
3. Вычисляют величину эмпирического критерия на основе параметров вариационного ряда Кэмп-
4. По таблице критических значений распределения находят теоретический (часто называют «критический») критерий согласия Кт при заданном значении а.
5. Делают вывод относительно проверяемой гипотезы о согласованности теоретического и эмпирического распределений:
а) если Кэмп < Кт, гипотезу принимают;
б) если К эмп > К т, гипотезу отвергают.
Поскольку категоричные суждения в статистике не принимаются, в случае Кэмп < Кт можно только утверждать, что принятая гипотеза не противоречит результатам наблюдения. Другими словами, проверка статистических гипотез позволяет отвергнуть гипотезу как неправильную, но не позволяет доказать, что она верна, лишь указывает на отсутствие опровержения со стороны опытных данных.
