Академия управления мвд россии

Вид материала

Учебник

Содержание Нормальный закон распределения Рис. 3.8.6. Кривые нормального закона распределения Динамический ряд Статистические данные о состоянии криминологической обстановки в регионе N A bcdefghij

Подобный материал:

• Темы контрольных работ Аппараты мвд, ГУ мвд, У мвд, ут мвд россии по Федеральным округам, 48.32kb.
• Положение о Штабе Главного управления мвд россии по Ростовской области общие положения, 212.4kb.
• Методические рекомендации по подготовке рефератов сотрудниками подразделений уголовного, 335.13kb.
• Нижегородская академия, 209.52kb.
• Функция прогнозирования миграционных процессов в системе управления мвд россии, 462.3kb.
• Нижегородская академия, 238.9kb.
• Нижегородская академия, 214.37kb.
• Ения, подразделениях Государственной противопожарной службы мвд россии, Первом управлении, 1898.24kb.
• Инструкция по организации учебного процесса в центре профессиональной подготовки территориального, 515.25kb.
• Рабочая программа дисциплины методы исследований в менеджменте направление подготовки, 262.36kb.

431

Для нашего эмпирического вариационного ряда (см. табл. 3.8.2) нужно подсчитать Кэмп> в качестве которого возьмем 5С². Для вы­числения х эмп необходимо сравнить эмпирические частоты вариационного ряда с теоретическими, рассчитанными Excel 5.0 для кривой нормального распределения при заданных значениях Хср и ст. Получаем, что эмп =3,52. По таблице значений крит при а = 0,01 и числе степеней свободы к = t - г -1=6, где t -количество интервалов, г - число параметров распределения, на­ходим = 16,8. Следовательно, нет оснований отвергать гипотезу о нормальном распределении возрастов осужденных в выборочной совокупности, так как эмп ^<')(^гкpи•

Итак, оценка эмпирического распределения сводится к реше­нию трех задач:

1) нахождению общего характера эмпирического распределения (построение полигона и вычисление основных показателей);

2) сглаживанию эмпирического распределения посредством из­вестного теоретического распределения, в зависимости от характера полученных показателей, вида полигона и навыков самого исследова­теля;

3) проверке степени близости эмпирического и теоретического распределений с помощью критерия согласия.

Поскольку генеральная совокупность вариационного ряда, представленного в табл. 3.8.2, соответствует нормальному закону рас­пределения (согласно нулевой гипотезе), рассмотрим более подробно свойства этого закона.

Нормальный закон распределения проявляется в тех случаях, когда случайная величина Х образуется в результате действия боль­шого числа взаимно независимых факторов, причем каждый фактор не доминирует над другими по степени своего влияния на X.

Кривая нормального распределения, или просто нормальная кривая, имеет холмообразный вид. В формулу кривой входят пара­метры М(х) - математического ожидания, и ст(х) - среднего квадрати-ческого отклонения. Математическое ожидание или Хср являются центром симметрии кривой, вокруг которого группируются случай­ные величины. При изменении кривая смещается вдоль оси X, сохра­няя свой вид. Так, на рис. 3.8.6 видно, что изменение Хср значения 20 на 15 сдвигает нормальную кривую влево по оси X.

432



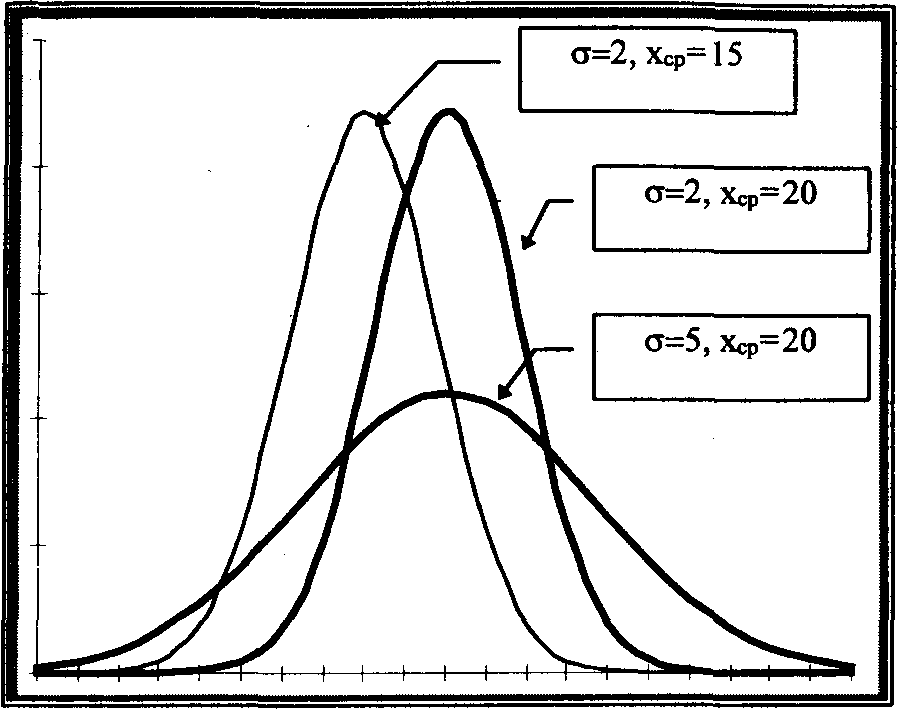
С изменением ст(х) вид кривой ме­няется: с ростом ст(х) кривая прижимается к оси Х и растягива­ется вдоль нее (большой разброс случайной величины X) (см. на рис. 3.8.6 кривую с от(х)= 5), с уменьшением о(х) кривая вытягивается вдоль оси ординат. Точки перегиба⁵⁴ у

кривой отстоят от М(х) на расстоянии ±

Рис. 3.8.6. Кривые нормального закона распределения

ст(х). Известно также правило, что:

• 95%распределения лежит между значениями М - 2ст; М + 2ст;
  
• более, чем 99% распределения заключено между М- Зет; М+ Зст.
  

Напомним, что у кривой нормального распределения М(х)=Мо(х)=Ме(х).

3. С помощью методов статистического анализа исследуют структуру и динамику преступности, определяют факторы, влияю­щие, на нее, оценивают на основе конкретных критериев эффектив­ность работы органов внутренних дел.

Основная цель статистического анализа заключается в установ­лении и измерении взаимосвязей и закономерностей изучаемых массовых явлений и процессов. К главным задачам относятся: 1) описание явления; 2) сопоставление и выявление закономерностей; 3) составление прогноза; 4) подготовка выводов.

Выявляя количественные взаимосвязи, соотношения и законо­мерности, статистический анализ помогает изучать и в определенной степени объяснять характер и причины явлений, условий и механизм их развития. Статистический анализ характеризует, что было и что есть. Но чтобы познать явление, надо знать не только прошлое и на­стоящее, но и иметь представление о будущем, о перспективах и тен-

⁵⁴ Точкой перегиба функции у = f(x) называется такая, в которой кривая из вогнутой становится выпуклой, и наоборот.

433

денциях развития явлений. Таким образом, статистический анализ имеет и прогностическую функцию.

Статистический анализ позволяет выявить «тревожные» момен­ты в характеристике преступности, положительные стороны и недос­татки в работе ОВД, слабые звенья (например, низкий уровень рас­крываемое™ преступлений, длительные сроки и низкое качество рас­следования и рассмотрения дел и т.д.), чтобы на основе этих данных своевременно принять решение, разработать меры по устранению не­достатков. В конечном итоге статистическая информация нужна именно для того, чтобы сделать практические выводы для улучшения организации работы.

Статистический анализ характеризуется применением разнооб­разных методов математической статистики: корреляционного, дис­персионного, факторного, кластерного и др.

Большинство статистических задач достаточно трудоемки и требуют большого количества рутинных вычислений, ограничиваю­щихся в целом ряде случаев простыми математическими операциями. Поэтому автоматизация решения такого класса задач просто необхо­дима.

К универсальным пакетам статистических программ можно от­нести: DataStat, MicroStat, MultiStat, P-Stat, SAS, Soritec, SPSS, STADIA, STATA, StatGraphics, Statistica, StatPro, StatView, Systat и др. Эти прикладные программы имеют различную структуру и интер­фейс с пользователем, обеспечивая широкий набор статистических процедур для анализа данных наряду с другими функциями (ввод и редактирование данных, графический анализ и др.).

Например, пакет StatGraphics содержит практически все функ­ции статистического анализа, великолепную графику и по обилию своих возможностей представляет большой интерес для специалиста-математика. В сравнении с StatGraphics небольшой пакет MicroStat более прост в использовании и включает лишь ряд функций для оце­нивания плотностей распределений, дисперсионного и регрессионно­го анализа и ряда др.

Для работы с «гигантскими» массивами данных и многоцелевого использования прекрасно зарекомендовал себя пакет SAS (Statistical Analysis System), который является лидером перечисленной группы стати­стических программ. Однако он требует для своей работы 10-16 Мбайт оперативной памяти, в зависимости от полноты используемых функций пакета, и не менее 120 Мбайт памяти на жестком диске.

434

Excel 5.0 для Windows представляет значительное количество разнообразных функций как для описательной, так и для производной статистики и анализа данных. В случае многомерного статистическо­го анализа, т.е. анализа со многими зависимыми переменными, Excel (версии 5.0 и 7.0) по своим возможностям ничем не уступает стан­дартным статистическим пакетам, указанным выше. Поэтому даль­нейший статистический анализ будем иллюстрировать расчетами в Excel 5.0 для Windows.

Характеристика динамических рядов. Общественные явления, в частности преступность и правонарушения, изучаемые статистикой, находятся в постоянном развитии и изменении. При изучении соци­ально-экономических процессов в развитии применяют ряды динами­ки.

Динамический ряд - последовательный ряд значений статисти­ческих показателей, характеризующих изменение общественных яв­лений во времени. Числовые значения показателей динамического ряда называются уровнями ряда.

С помощью динамических рядов изучение закономерностей развития социально-экономических явлений осуществляется в сле­дующих направлениях:

• характеристика уровней развития изучаемых явлений во вре­мени;
  
• измерение динамики изучаемых явлений посредством систе­мы статистических показателей;
  
• выявление и количественная оценка основной тенденции (тренда) развития;
  
• изучение периодических колебаний;
  
• экстраполяция и прогнозирование.
  

Основным условием для получения правильных выводов при анализе динамики является сопоставимость его элементов. Несо­поставимость в динамических рядах вызывается различными при­чинами. Это могут быть разновеликость показаний времени, не­однородность состава изучаемых совокупностей во времени, из­менения в методике первичного учета и обобщения исходной ин­формации, различия применяемых в отдельные периоды единиц

измерения и др.

В зависимости от характера уровней ряда различают два вида динамических рядов: моментные и интервальные.

435

Моментным называется ряд динамики, уровни которого характери­зуют состояние явления на определенный момент времени (см. табл. 3.8.6).

Таблица 3.8.6 Пример моментного ряда

Момент времени	Годы
	1.01.95	1.01.96	1.1.97	1.1.98
Штат ОВД	160	165	166	170

В каждом последующем уровне этого ряда содержится полно­стью или частично предыдущий уровень. Уровни ряда удобно срав­нивать для изучения развития изучаемого явления во времени.

Интервальным называется такой ряд динамики, уровни которо­го характеризуют размер явления за отдельные периоды времени (см. табл. 3.8.7). Уровни интервального ряда не содержатся в предыдущих и последующих показателях. Поэтому важное значение имеет сумми­рование этих уровней. Свойство суммирования уровней за последова­тельные интервалы времени позволяет получать ряды динамики более укрупненных периодов.

Таблица 3.8.7 Пример интервального ряда

Показатель	Годы
	1995	1996	1997	1998
Количество зарегистрирован­ных убийств	48	60	78	90

Для количественной оценки динамики социально-экономических явлений применяются статистические показатели. К основным показате­лям относятся: абсолютный прирост, темп роста и темп прироста.

Базисный абсолютный прирост AYo вычисляется как разность между сравниваемым уровнем y( и уровнем, принятым за постоянную базу сравне­ния yq, а именно AYg = y( - Y„ (3.8.15). Например, базисный абсолютный прирост зарегистрированных убийств в 1997 г. по сравнению с 1995 г. со­ставляет ЛУб = 78 - 48 = 30 (данные и далее берутся из табл. 3.8.7).

Цепной абсолютный прирост АУц представляет собой разность между сравниваемым уровнем y( и уровнем, который ему предшест-

436

вует , т. е. AY„ = y( - Уц (3.8.16). Так, цепной абсолютный прирост зарегистрированных убийств в 1997 г. по сравнению с 1996 г. состав­ляет ЛУц=78-60=18.

Распространенным статистическим показателем динамических рядов является темп роста. Он характеризует отношение двух уровней ряда и может выражаться в виде коэффициента или в процентах. Ба­зисный темп роста Трб( исчисляется делением сравниваемого уровня y( на уровень Yo, принятый за постоянную базу сравнения. Формула имеет вид: Трб» = y( / Yo (3.8.17). Например, темп роста зарегистриро­ванных убийств в 1997 г. по сравнению с базовым 1995 г. равняется

Трб ==78/48=1,63.

Цепной темп роста исчисляется делением сравниваемого уровня

на предыдущий уровень, а именно Трц i = y( / Yt-i (3.8.18). Так, темп роста зарегистрированных убийств в 1997 г. по сравнению с 1996 г.

равняется Трц( = 78/60 =1,3.

Темпы прироста характеризуют абсолютный прирост в относи­тельных величинах. Базисный темп прироста Тпб( вычисляется деле­нием сравниваемого абсолютного прироста ДУб на уровень, принятый за постоянную базу сравнения Yo, то есть Тпб(=АУб/Уо (3.8.19). Так, базисный темп прироста зарегистрированных убийств в 1995 г. со­ставляет Тпбз = 30/48 = 0,625. Часто темп прироста исчисляют не в долях, а в процентах. В этом случае абсолютный темп прироста пока­зывает, на сколько процентов изменился сравниваемый уровень с уровнем, принятым за базу сравнения. Полученный результат в долях

умножается на 100%, тогда Тпбз= 62,5 %.

Аналогично вычисляется цепной темп прироста:

Тпщ=ДУц (/у».] (3.8.20). Подсчитаем темп прироста зарегистри­рованных убийств в 1997 г. по сравнению с 1996 г.: Тпцз =16/60=0,267, или 26,7% . Кроме того, для сравнения динамических рядов используются средние величины: средний уровень, средний аб­солютный прирост, средние темпы роста и прироста.

В интервальных рядах динамики средний уровень Yep опреде­ляется делением суммы уровней на их число, т. е. подсчитывается средняя арифметическая по формуле (3.8.2). Так, для интервального ряда, представленного в таблице 3.8.7, Yep = (48+60+78+90)/4 = 69 зарегистрированных убийств в год.

437

Для моментных рядов средний уровень определяется как сред­няя хронологическая с равностоящими датами времени. Она равна сумме уровней ряда, деленной на число уровней без единицы; при этом начальный и конечный уровни должны быть взяты в половин­ном размере, так как число дат (моментов) обычно бывает на единицу больше, чем число периодов:

у ½+у2+уз+......+у„/2

Yxp=———————————————— . (3.8.21)

n-1

Подсчитаем средний уровень для моментного ряда, представленно­го в табл. 3.8.6. Yxp = (160/2+165+166+170/2)/(4-1)= 165,3» 165 чел.

В моментном ряду динамики с неравноотстоящими датами t;

средний уровень определяется по формуле средней взвешенной 3.8.3, в которой вместо частот f; нужно поставить t,.

Средний абсолютный прирост определяется как сумма абсо­лютных цепных приростов, деленная на их число. Так, для ряда из табл. 3.8.7 абсолютный прирост равняется:

АУцср = [(60-48) + (78-60)+(90-78)]/3 = 14 зарегистрированных убийств.

Средний темп роста Трср вычисляется по формуле 3.8.5 средней геометрической, а средний темп прироста определяется на основе взаимосвязи между темпом роста и прироста,

а именно: Тпср = Трср - 1 . (3.8.22)

Так, для ряда из табл. 3.8.7 Трср = 1.23 и Тпср = 0,23 (или 23 %).

Изучение динамических рядов с помощью диаграмм. Важной стороной анализа динамических рядов является определение тенден­ции их поведения во времени. Иногда лишь одно только построение динамического ряда без всякой дополнительной обработки информа­ции выявляет общее направление или тенденцию (тренд) развития яв­ления. Но чаще бывают случаи, когда тенденция развития явления яв­но не прослеживается, так как уровни ряда колеблются то в сторону уве­личения, то в сторону уменьшения, или наоборот. Одним из способов выявления тенденций выступает аналитическая замена динамического ряда теоретической кривой сглаживания, параметры (коэффициенты) которой находятся методом наименьших квадратов.

Сущность метода заключается в том, что для выбранной функ­ции сглаживания определяются параметры, при которых сумма квад­ратов отклонений расчетных значений уровней от их действительных

438

значений должна быть минимальной. Excel 5.0 позволяет проводить подобные расчеты.

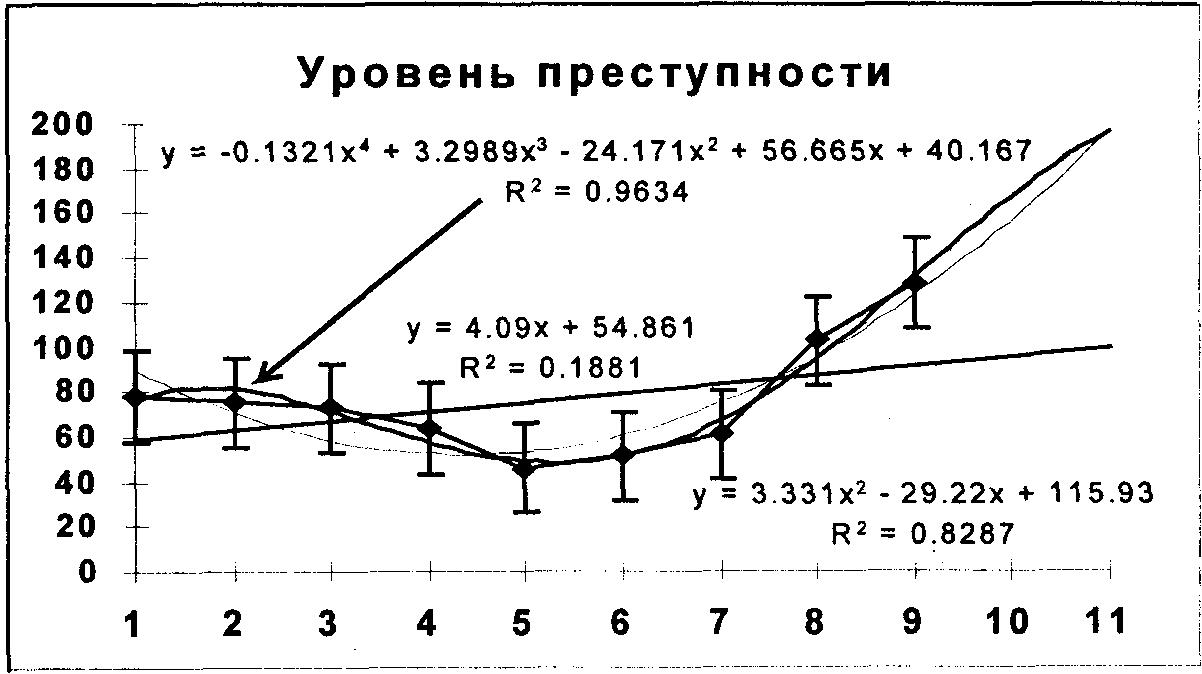
На преступность влияют многие факторы. Показатели, отра­жающие некоторые из них, приведены в табл. 3.8.8. Они называются факторными признаками, а уровень преступности является результа­тивным признаком. Рассмотрим в качестве иллюстрации динамиче­ский ряд «Уровень преступности».

Таблица 3.8.8

Статистические данные о состоянии криминологической обстановки в регионе N

	A BCDEFGHIJ
1	ГОДЫ 123456789
2	Уровень преступности	78	75,2	72,7	63,7	46	50,9	60,8	102,4	128,1
3	Доля городского населения	0,8	0,805	0,807	0,81	0,81	0,815	0,82	0,83	0,836
4	Доля несовершеннолетних	6,8	6,4	5,8	5,4	5,5	5,3	6,1	6,7	6,8
5	Доля ранее судимых (на 10 тыс.)	154,7	151,3	149	144,9	137,9	132,2	146,3	164,2	170,9
6	Доля незанятых (на 100 тыс.)	110,9	100,9	103,2	95,7	77,7	96,3	82,3	117	126,6
7	Доля наркоманов (на 100 тыс.)	2	2,3	4,3	6	6,9	7,9	11,7	16,2	18,9
8	Доля иммигрантов (на одну тыс.)	16,2	16,4	15,1	16,6	19,1	21,1	22,3	23,3	22
9	Потребление алкоголя	6	6	5,9	5,2	4,6	4,7	5,1	6,2	6,6
10	Выпуск промышленной продукции	2,7	2,7	2,8	3,1	3,1	3,2	3,2	3,1	3
11	Выпуск сельхозпродукции	0,4	0,27	0,26	0,37	0,36	0,34	0,31	0,31	0,26
12	Плотность сотрудников ОВД (на 10 тыс.)	28,6	30,4	28,5	27,6	27,5	26,2	26,3	26,4	27,8
13	Плотность сотрудников УР (на 10 тыс.)	2,2	2,23	2,36	2,3	2,3	2,21	2,2	2,3	2,4

Сущность метода заключается в том, что для выбранной функции сглаживания определяются параметры, при которых сумма квадратов от­клонений расчетных значений уровней от их действительных значений должна быть минимальной. Excel 5.0 позволяет проводить подобные расче­ты. Для этого выделяем интервал ячеек A2J2, в которых находятся уровни динамического ряда, и обращаемся к «Мастеру диаграмм», который строит график эмпирического ряда в диалоговом режиме.

439

Чтобы вызвать команду «Линия тренда», выделяем точки гра­фика. В диалоговом окне «Линия тренда» имеется набор аналитиче­ских функций, которые могут смоделировать поведение ряда динами­ки уровня преступности. Выбираем несколько типов тренда, вводя их последовательно на диаграмму. Возьмем в качестве аналитических кривых прямую линию, параболу и полином четвертой степени.

Кроме того, выбираем режим прогноза на два периода (года) вперед, указывая Excel 5.0 на необходимость «Показывать уравнение на диаграмме» и «Показывать значение R-квадрат на диаграмме».

Наша задача - оценить, какая из теоретических кривых лучше описывает экспериментальную кривую. Таким оценочным показате­лем является критерий R-квадрат (показатель, говорящий о точности прогноза, меняющийся в пределах 0 < R² < 1). Кривая, обладающая наиболее высоким R-квадратом, лучше описывает явление. Как видно из рис. 3.8.7, такой кривой является полином четвертой степени, имеющий показатель R-квадрат, равный 0,9634.