Академия управления мвд россии

Вид материала

Учебник

Содержание Рис. 3.8.7. Оценка близости линии тренда к экспериментальной кривой Прогнозирование динамических рядов методом экстраполя­ции. Первый этап Рис. 3.8.8, Построение сетки на графике Cdefghi jk l Статистическая зависимость уровня преступности от нагрузки на одного сотрудника милиции Корреляционной связью Корреляционный анализ Построение таблицы парных корреляций. Таблица 3.8.11 Коэффициенты корреляции с лагом 0,1, 2 Понятие регрессионного анализа. Регрессионный анализ Прогнозирование уровня преступности с лагом 0. Таблица 3.8.13 Построение уравнения множественной регрессии с лагами 1 и 2 A bcdefghi Вопросы для контроля и самопроверки Вопросы для контроля и самопроверки 4.1. Принципы применения информационных тех­нологий в деятельности органов внутренних дел

Подобный материал:

• Темы контрольных работ Аппараты мвд, ГУ мвд, У мвд, ут мвд россии по Федеральным округам, 48.32kb.
• Положение о Штабе Главного управления мвд россии по Ростовской области общие положения, 212.4kb.
• Методические рекомендации по подготовке рефератов сотрудниками подразделений уголовного, 335.13kb.
• Нижегородская академия, 209.52kb.
• Функция прогнозирования миграционных процессов в системе управления мвд россии, 462.3kb.
• Нижегородская академия, 238.9kb.
• Нижегородская академия, 214.37kb.
• Ения, подразделениях Государственной противопожарной службы мвд россии, Первом управлении, 1898.24kb.
• Инструкция по организации учебного процесса в центре профессиональной подготовки территориального, 515.25kb.
• Рабочая программа дисциплины методы исследований в менеджменте направление подготовки, 262.36kb.

Рис. 3.8.7. Оценка близости линии тренда к экспериментальной кривой

Кроме того, оценку близости теоретической и эксперименталь­ной кривых дают планки погрешностей. Чтобы их построить на гра­фике, нужно выделить точки экспериментальной кривой и выполнить команду «Планки погрешностей».

На диаграмме появляются планки погрешностей (их центром являются экспериментальные точки), характеризующие интервал, в

440

который должна попасть теоретическая кривая. Как видно из рис. 3.8.7, в этот интервал полностью вписываются кривая-полином четвертой степени и парабола, но у нее R² = 0,8287.

Прогнозирование динамических рядов методом экстраполя­ции.

Метод экстраполяции - это нахождение по известным значени­ям динамического ряда других значений, лежащих за его пределами.

При экстраполяции исследователь переносит выводы, которые он сделал при изучении тенденций развития явления в прошлом и на­стоящем, на будущее, т.е. здесь лежит предположение об определен­ной стабильности факторных признаков, влияющих на развитие дан­ного явления. Прогноз разрабатывается с учетом результатов экстра­поляции, но с привлечением дополнительной информации, не содер­жащейся в самом динамическом ряду. Это так называемая качествен­ная информация, подтверждающая объективное существование ос­новной тенденции и обоснованность переноса ее в будущее.

При разработке экстраполяционных прогнозов статистическими методами выделяются два этапа. Первый этап - это обоснование существования тенденции развития явления во времени и выбор аналитической формы ее описания. Второй этап - это анализ и обоснование целесообразности распространения тенденции в бу­дущее и собственно само аналитическое прогнозирование значений динамического ряда на заданный период времени. Как правило, этот период - довольно короткий: один - три года.

Как видно из рис. 3.8.8, мы выбрали аналитическую кривую (полином четвертого порядка), заменили ей динамический ряд и про­должили ее на два периода, а именно на 10-й и 11-й годы, тем самым выполнив два этапа экстраполяционного прогноза.

Наша задача - определить конкретные прогнозные значения уровня преступности на 10-й и 11-й годы. Существует несколько спо­собов.

Первый способ - построение сетки на rpaf, we. Сотрем лишние линии тренда, выделяя их и нажимая клавишу Del. Чтобы построить сетку, нужно выполнить команду «Сетка». В позициях «Ось X» и «Ось Y» пометим крестиком пункты «основная сетка» (она - более крупная и жирная) и «вспомогательная сетка». Для удобства измерения изме­ним шкалу сетки. Введем числа: минимум - 165, максимум - 200, ос­новная единица - 4, вспомогательная единица - 0,5, пересечение с

441

осью X в значении - 165. Для удобства обозрения можно изменить цвет вспомогательной сетки.

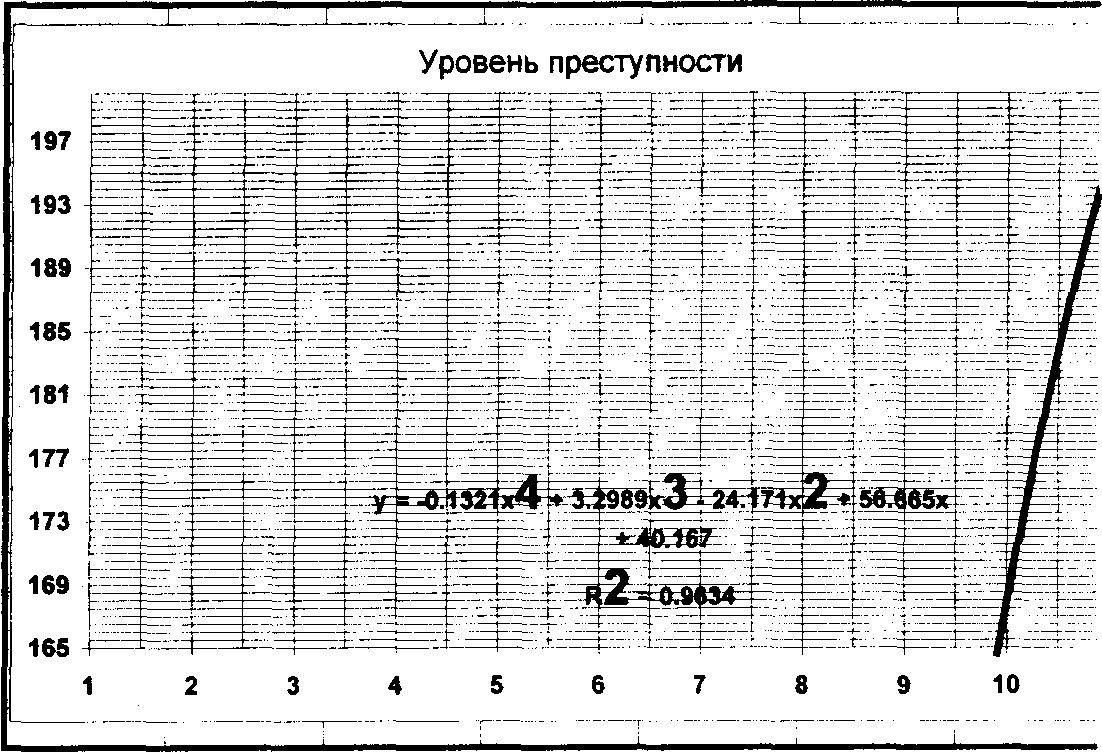
Рис. 3.8.8, Построение сетки на графике

В результате можно утверждать, что уровень преступности в 10-м периоде (году) будет составлять 169 преступлений в расчете на 10 тыс. чел., а в 11-м - 196 преступлений.

Второй способ определения прогнозных значений заключается в расчете значений теоретической кривой четвертой степени. Для удобства расчета переносим динамический ряд уровня преступности в соседний рабочий лист Excel 5.0, помещаем в ячейки B1:L4 все воз­можные значения переменной X, входящей в формулу полинома чет­вертой степени. Далее с помощью «Мастера функций» вычисляем теоретическое значение статистической функции «Тенденция» в пер­вом периоде (году) и копируем расчетную формулу в ячейки C6:L6 для остальных периодов.

Результат представлен в таблице 3.8.9. Расчет тенденции показы­вает, что уровень преступности в 10-м периоде равняется 167,8, в 11-м периоде он достиг 195,9 преступлений в расчете на 10 тыс. чел.

Общие понятия корреляционного анализа. Важнейшим услови­ем деятельности в сфере борьбы с преступностью является знание причинно-следственных отношений между показателями, характери­зующими состояние, динамику и структуру социально-экономических

442

процессов, преступности и функционирования органов внутренних

дел.

Таблица 3.8.9 Расчет теоретической кривой

	А	В	CDEFGHI JK L
1		1	2	3	4	5		7	.		10	11
2	X2 /\	1	4	9	л а 16	QC 25	Oft 00	49	CtA 64	Q-1 o1	100	121
3	X3 Л	1		27	CtA 64	125	0»1Д 21b	0 А О 343	c-19	79Q / £-v	1000	1331
4	X4 /\	1	л а Ю	0*1 01	ОСД 00	CQC 625	'lOQft izyo	2401	4096	с ее л 000 1	•щллп luuuu	14641
5	Уровень преступности	7Q /О	•7С 0 ' (	72,7	С*Э «7 о3,7	46	СЛ Q *J\J,y	ДЛ Q ou,o	102,4	Л OQ Л 1Zo,1
6	Полином четвертого порядка	«7G /О	81,1	71	57,4	49	51,4	ftft Q ЬЬ,о	94,6	A Qrt ft 1oU,b	л д-7 Q 167,0	195,9

Однако в настоящее время уже недостаточно лишь констатиро­вать наличие существующих связей, их нужно измерять. Количест­венное их измерение и получаемые на этой основе выводы во многом определяют выбор конкретных форм и методов деятельности в сфере борьбы с преступностью.

Для точного выражения зависимости между переменными (признаками, показателями) в математике применяется понятие функции, функциональной зависимости Y=F(x), где каждому значе­нию одной величины «х» соответствует определенное значение вто­рой величины «у». Например, длина тормозного пути Y зависит от скорости автомобиля Х в момент торможения: Y = a*fS* у*Х². При этом в формулу определения длины тормозного пути эта ско­рость входит в квадрате. В формулу также введены коэффициенты, учитывающие механические свойства рабочей поверхности колеса и поверхности дороги, состояние дорожного покрытия и продольного уклона дороги. Эти постоянные коэффициенты берутся из таблиц.

По отношению к событиям функциональная зависимость всегда выступает в виде причинной, т.е. наступление одного события (причины, в нашем случае - конкретное значение скорости в момент торможения) всегда влечет наступление другого (следствия, в нашем примере - определенная длина тормозного пути).

При анализе зависимостей в социальной сфере в большинстве случаев нельзя установить однозначного соответствия между какими-либо социальными признаками. Значению некоторого социального

443

признака может соответствовать множество значений другого призна­ка. В этом случае какое-либо событие (причина) не обязательно приво­дит к определенному результату (следствию). Изменение признака со­ответствует множеству изменений других признаков, колеблющихся возле некоторой средней величины. Такие зависимости называются стохастическими. Так, улучшение некоторых социально-экономиче­ских условий жизни населения не обязательно в каждом конкретном случае приводит к снижению преступности, что обусловлено действи­ем множества других факторов, т.е. стохастической природой преступ­ности и ее связью с другими, не только социальными, явлениями.

Приведем еще один пример. Практика подтверждает, что в тех регионах, где количество преступлений, приходящихся на одного ра­ботника милиции (нагрузка), больше, там ниже процент раскрывае-мости преступлений. Однако эта закономерность проявляется лишь статистически, а не функционально.

Статистическая зависимость уровня преступности от нагрузки на одного сотрудника милиции

Y Х	30	35	40	45
100	5	4	3
110	4	3	3	4
120	1	3	3	4
130	-	-	-	2

Рассмотрим табл. 3.8.10. В ней приведены статистические данные по некоторому региону: Y - количество преступлений в расчете на 10 тыс. человек населения (уровень преступности), Х - количество пре­ступлений, приходящихся на одного работника милиции (нагрузка). В регионе выбирались 10 городов с примерно одинаковой нагрузкой на одного работника милиции (всего 40 городов).

Как видно из таблицы Таблица 3.8.10 3.8.10, при нагрузке Х = 30

уровень преступности в пяти городах равен 100, в четырех городах - Y = 110, в одном городе - Y = 120, т.е. одному значению Х соответствует несколько значений Y. С дру­гой стороны, уровень пре­ступности Y = 100 отмечен в 12 городах с различной на­грузкой: в пяти городах - Х = 30, в четырех городах - Х = 35, в трех городах - Х = 45, т.е. одному значению Y соответствует несколько значений X.

Тенденция проявляется лишь в среднем. Так, для Х = 30 среднее значение Yep = (100*5 + 110*4 + 120*1)/10 = 106. Поступая аналогич­ным образом, получим:

444

Y	100	110	120	130
Х	34	37	40	43

X	30	35	40	45
Y	106	109	112	118

Корреляционной связью называется такая статистическая зави­симость, которая проявляется в виде тенденций для средних величин значений показателей, при этом каждому значению показателя, вы­бранного в качестве независимой переменной или факторного при­знака (X), соответствует множество значений другого показателя, вы­бранного в качестве зависимой переменной или результативного при­знака (Y), и наоборот.

Особенность корреляционных связей заключается в том, что они (в отличие от функциональных связей) являются неполными. Анализируя, например, зависимость между нагрузкой (факторным признаком) и раскрываемостью преступлений (результативным при­знаком), приходим к выводу, что на раскрываемость действуют и дру­гие факторы, причем они оказывают влияние в разных направлениях (так, высокий уровень профессиональной подготовленности сотруд­ников милиции будет положительно воздействовать на результаты их работы, а слабая оснащенность техническими средствами, напротив, будет отрицательно влиять на результаты их деятельности).

Для изучения корреляционной связи разработаны специальные методы, и в частности корреляционный анализ.

Корреляционный анализ - комплексное использование в опреде­ленной последовательности совокупности различных статистических методов обработки информации, позволяющее при выполнении неко­торых условий найти форму, направление и величину или тесноту взаимосвязей между признаками.

По форме корреляционные связи могут быть линейными и кри­волинейными. Для корректного применения корреляционного анали­за требуется обоснование близости распределения значений фактор­ного и результативного признаков к нормальному и формы связи к линейной. В противном случае необходимо использовать специаль­ные приемы анализа или другие коэффициенты связи.

Следующим условием применимости корреляционного анализа является условие достаточности объема значений признаков и их од­нородности. Чем хуже выполняется это условие, тем более сложный математический аппарат надо привлекать для получения надежных и достоверных выводов.

445

По направлению (типу) корреляционные связи можно разделить на прямые (положительные) и обратные (отрицательные). При пря­мой связи увеличение факторного признака ведет к увеличению ре­зультативного признака (например, связь между нагрузкой на одного сотрудника милиции и уровнем преступности), а при обратной - уве­личение факторного признака ведет к уменьшению результативного признака (например, связь между нагрузкой на одного сотрудника милиции и процентом раскрываемое™ преступлений).

Сила или теснота корреляционной связи характеризуется раз­личными коэффициентами, измеряющими эту связь. Так, для метри­ческих шкал используется линейный коэффициент корреляции (Пирсона) - г. Коэффициент корреляции - величина относительная, он выражается в долях единицы от -1 до +1.

Обычно считается, что г < 0,3 указывает на слабую связь, при 0,3 < г < 0,5 связь признается умеренной, при 0,5 < г < 0,7 корреляция является значительной, а при 0,7 < г < 0,9 - сильной и при г > 0,9 -очень сильной, близкой к функциональной связи.

Следует отметить, что коэффициент корреляции позволяет оп­ределить не только тесноту, но и направление связи ( на это указыва­ют знаки «+» или «-«).

Корреляционный анализ не заканчивается только подсчетом г. Необходимо проверить значимость коэффициента корреляции при за­данном уровне. Если г > г кр. (критическое значение г кр. находят по специальным таблицам), то полученному результату можно доверять;

если г< г кр., то рассчитанному коэффициенту корреляции доверять

нельзя.

На уровень преступности влияет множество факторных призна­ков. К' ним относятся социально-экономические, географические и климатические, демографические и другие признаки, а также призна­ки, характеризующие силы и средства, степень организованности

ОВД.

Пусть п - число этих признаков. Тогда Y = Y(Xl,X2,X3,...Xn).

Задача корреляционного анализа - выявить те факторные признаки, которые наиболее существенно влияют на результативный признак Y,

а остальными можно пренебречь.

Пусть, например, после вычислений коэффициентов корреля­ции оказалось, что Y = Y(X9, X21, Х45). Тогда руководитель органа внутренних дел при разработке плана мероприятий должен в первую

446

очередь включать в него такие, которые влияют на перечисленные факторные признаки.

Для нас представляет интерес рассмотрение корреляционных зависимостей динамических рядов. Факторные и результативные при­знаки могут меняться во времени, т.е. представлять динамические ря­ды. Между ними также можно количественно измерить тесноту связи, используя коэффициенты корреляции. Однако, чтобы использовать методы корреляционного анализа, надо выполнить ряд условий.

Динамическим рядам свойственны колебания различных типов. Первый тип - сезонные, примерно одинаковые внутригодичные коле­бания. Второй тип - трендовые, или длительные, колебания, выра­женные постоянным увеличением (уменьшением) средних уровней, как проявлением общей тенденции развития явления. Третий тип -эксцессы, нерегулярные колебания, вызванные такими факторами, как стихийные бедствия, неурожаи, военные действия и т.п. Четвер­тый тип - колебания циклические, повторяющиеся через длительные и не обязательно одинаковые промежутки времени. Эти колебания проявляются в результате изменения хозяйственной деятельности, скачка научно-технического прогресса и т.п.

Корреляцию динамических рядов можно применять только для однотипных динамических рядов, имеющих одинаковый тип колеба­ний. Это первое условие.

Вторым условием применимости корреляционного анализа яв­ляется замена эмпирических данных (уровней) динамических рядов расчетными значениями. Для этого каждый эмпирический ряд надо выровнять теоретической кривой, наиболее близко описывающей ди­намический ряд. Только после замены эмпирических уровней на рас­четные можно вычислять коэффициенты корреляции г.

При коррелировании рядов динамики надо обращать внимание на возможность изменений уровней одного ряда динамики на уровни другого со сдвигом во времени. Встречаются такие взаимосвязи между явлениями, когда изменения одного явления вызывают изменения дру­гого не сразу, а через какой-то период времени (так, изменение структу­ры органа внутренних дел может сказаться на результативности работы с запаздыванием). В этом случае необходимо совместить динамические ряды, чтобы устранить сдвиг. Этот сдвиг называется лагом.

Для динамических рядов можно также установить, усиливается или ослабевает связь между рядами динамики во времени, т.е. увели­чивается или уменьшается коэффициент корреляции между анализи-

447



руемыми явлениями. Для ответа на этот вопрос иногда достаточно разделить каждый из сопоставляемых рядов динамики на два во вре­мени и для каждой пары новых рядов вычислить коэффициенты кор­реляции.

Построение таблицы парных корреляций. Вычисление коэф­фициентов корреляции будем проводить на отдельном рабочем листе. Для получения коэффициентов корреляции выполняем следующую последовательность действий:

• вызываем «Мастера функций» и среди статистических функ­ций активизируем функцию «Корреляция»;
  
• в строку «массив 1» вводим диапазон динамического ряда «Уровень преступности», являющегося результативным или зависи­мым признаком;
  
• в строку «массив 2» вводим данные факторного или независи­мого признака «Доля городского населения».
  
• нажимаем на клавишу «Закончить», чтобы получить коэффи­циент корреляции, показывающий степень влияния доли городского населения на уровень преступности.
  

В результате в ячейке В2 появляется г = 0,66 (см. табл. 3.8.11). Скопируем формулу коэффициента корреляции, находящуюся в ячей­ке В2, в диапазон ячеек ВЗ:В12.

Таблица 3.8.11 Коэффициенты корреляции с лагом 0,1, 2

А	В	С	D	Е	F	G	Н	I
Корреляция уровня преступности	0	1	2	0	1	2	макс	лаг
Доля городского населения	0,66	0,72	0,71	0,66	0,72	0,71	0,72	1
Доля несовершеннолетних	0,80	0,71	0,07	0,80	0,71	0,07	0,80	0
Доля ранее судимых (на 10 тыс.)	0,96	0,71	-0,28	0,96	0,71	0,28	0,96	0
Доля незанятых (на 100 тыс.)	0,91	0,43	-0,36	0,91	0,43	0,36	0,91	0
Доля наркоманов (на 100 тыс.)	0,65	0,73	0,73	0,65	0,73	0,73	0,73	2
Доля иммигрантов (на 1 тыс.)	0,32	0,67	0,89	0,32	0,67	0,89	0,89	2
Потребление алкоголя (на душу)	0,91	0,51	-0,38	0,91	0,51	0,38	0,91	0
Выпуск промышленной продукции	-0,22	0,13	0,54	0,22	0,13	0,54	0,54	2
Выпуск сельхозпродукции	-0,49	-0,29	0,04	0,49	0,29	0,04	0,49	0
Плотность сотрудников ОВД (на 10 тыс.)	0,12	-0,33	-0,64	0,12	0,33	0,64	0,64	2
Плотность сотрудников УР (на 10 тыс.)	0,57	-0,17	-0,76	0,57	0,17	0,76	0,76	2

448

Результаты расчета представлены в табл. 3.8.11 в колонке В. Проведенные расчеты показывают, что наиболее сильное влияние на преступность оказывают три признака: доля ранее судимых (г4 = 0,96), доля незанятых (г5 = 0,91), потребление алкоголя (rg= 0,91). По­этому руководитель органа внутренних дел должен в первую очередь обратить внимание на эти показатели в текущем году (девятом перио­де).

Будем считать, что указанные три признака проявляют себя по­стоянно, без запаздывания. Поэтому эти три параметра наиболее ак­тивны в период с лагом 0.

Возникает вопрос, какие факторные признаки проявят себя в следующем году (десятом периоде), если для перечисленных призна­ков был разработан комплекс мероприятий с целью снижения их влияния на преступность. Чтобы определить, какие признаки проявят себя на следующий год с лагом 1, нужно сдвинуть слева направо динамический ряд «уровень преступности» на один год, но поскольку данных за десятый период нет, количество его членов станет равным восьми. Что касается факторных признаков, то они сдвигаются справа налево на один период, исключая текущий год. Таким образом, число их уровней также станет равным восьми.

Подсчитываем коэффициенты корреляции для лага 1. Результа­ты расчета представлены в столбце С табл. 3.8.11. Как видно из таб­лицы, в следующем (десятом) периоде влияние указанных ранее трех признаков снизилось (очевидно, из-за активной работы органа внут­ренних дел), но усилилось влияние таких признаков, как доля нарко­манов и доля городского населения (см. столбец С табл. 3.8.11).

Повторяем те же операции для лага 2. т.е. сдвигаем динамиче­ские ряды на два периода. На основе рассчитанных коэффициентов корреляции вычислим влияние факторных признаков в 11-м периоде. Как видно из табл. 3.8.11 (колонки D), наиболее существенно влияю­щими на преступность в 11-м периоде являются доля иммигрантов (г = 0,89), плотность сотрудников УР (г = -0,76), доля наркоманов (г = 0,73) и по-прежнему доля городского населения (г = 0,71).

Далее в столбцы Е, F, G вводим абсолютные значения коэффи­циентов корреляции (т.е. без знака «минус»). Эту операцию выполняет «Мастер функций», применяя к формулам, стоящим в столбцах В, С и D, математическую функцию ABS.

Находим теперь максимальное значение коэффициентов корре­ляции для каждого признака, в зависимости от лагов. Эту операцию

449

выполняет «Мастер функций», применяя к формулам, стоящим в столбцах Е, F, G, статистическую функцию «Макс». Результаты расче­та приведены в столбце Н табл. 3.8.11.

Теперь наша задача заключается в том, чтобы определить, ка­кому лагу соответствует максимум, находящийся в ячейках столбца Н. В принципе это можно сделать визуально и ввести в колонку 1 зна­чения лагов вручную. Однако это можно выполнить с помощью логи­ческой функции «ЕСЛИ». Снова заполнение столбца 1 выполнит «Мастер функций». В окончательном виде имеем табл. 3.8.11, которая позволяет провести анализ влияния факторных признаков на резуль­тативный признак в различные периоды времени.

Понятие регрессионного анализа. После определения наибо­лее существенных факторных признаков, влияющих на результатив­ный признак, не менее важно установить их математическое описание (уравнение), дающее возможность численно оценивать результатив­ный признак через факторные признаки.

Уравнение, выражающее изменение средней величины резуль­тативного признака в зависимости от значений факторных признаков, называется уравнением регрессии.

Регрессионный анализ - комплексное использование в опреде­ленной последовательности различных статистических методов обра­ботки информации, позволяющее при некоторых условиях найти вид уравнения регрессии и вычислить значения результативного признака Y по значениям факторных признаков.

Обычно уравнение регрессии представляется в виде следующей зависимости (Х9, Хгь Х»5 взяты в качестве иллюстрации):

¥= а + Ь *Х, + c*Xi + d*X4s.

Здесь а, Ь, с, d - неизвестные коэффициенты, которые опреде­ляются методами регрессионного анализа. Уравнение же называется уравнением множественной линейной регрессии.

Иногда достаточно выбрать один наиболее существенный при­знак и найти математическую зависимость между результативным признаком и выбранным факторным признаком, например: Y = а + Ь*Ху (прямая линия) или ¥= а + b*Xy + c*X²y (парабола). Эти уравне­ния называются уравнениями парной или простой регрессии.

Естественно, оценка результативного признака без учета ос­тальных факторных признаков (в нашем примере - Хгь Х4э) будет бо­лее грубой, но расчеты - менее трудоемкими, и иногда такой прибли­женной оценки бывает достаточно.

450

Качеством построения уравнения регрессии является средняя ошибка аппроксимации или стандартизированная ошибка оценки.

Итак, проведение регрессионного анализа позволяет разделить его на три этапа:

1) выбор формы зависимости (вида уравнения) на основе стати­стических данных;

2) вычисление коэффициентов выбранного уравнения;

3) оценка достоверности выбранного уравнения.

Используя уравнения регрессии, можно прогнозировать поведе­ние различных показателей, например уровня преступности, если имеются статистические или прогнозные данные о факторных при­знаках, влияющих на него.

Прогнозирование уровня преступности с лагом 0. В текущем году на преступность наиболее сильное влияние оказали такие фак­торные признаки, как «уровни ранее судимых» (г4=0,96), «уровни не­занятых» (г5=0,91), «потребление алкоголя» (г»=0,91). Будем их учиты­вать при построении уравнения регрессии.

Для этого дополним табл. 3.8.11 рядами динамики «уровни ра­нее судимых (на 10 тыс.)», «доля незанятых (на 100 тыс.)», «потребление алкоголя (на душу населения в литрах)» из табл. 3.8.8. В результате приходим к табл. 3.8.12.

Таблица 3.8.12 Построение уравнения множественной регрессии с лагом О

	А	В	С	D	Е	F	G	Н	I	J	К	L
1	X	1	2	3	4	5	6	7	8	9	10	ii
2	х*х	1	4	9	16	25	36	49	64	81	100	121
3	х*х*х	l	8	27	64	125	216	343	512	729	1000	1331
4	х*х*х*х	1	16	8]	256	625	1296	2401	4096	6561	10000	14641
5	Уровень преступ­ности	78	75,2	72,7	63,7	46	50,9	60,8	102,4	128,1
6	Полином четвер­той степени	75,8	81,1	71,0	57,4	49,0	51,4	66,8	94,6	131	167,8	195,9
7	Доля ранее судимых	154	151	149	144,9	138	132	146	164,2	170,9	186,9	206,1
8	Доля незанятых	111	101	103	95,7.	77,7	96,3	82,3	117	126,6	144,2	167,6
9	Потребление ал­коголя	6	6	5,9	5,2	4,6	4,7	5,1	6,2	6,6	7,45	8,53
10	Множественная регрессия	86,4	72,7	71,2	65,8	46,1	48,1	59,6	106,	122	155	196,1

15*

451

Поскольку у трех выделенных факторных признаков нет данных за 10-й и 11-й периоды, используем метод экстраполя­ции. Однако сначала необходимо изучить три динамических ря­да с помощью диаграмм. Эта утомительная процедура показы­вает, что полином четвертой степени описывает кривые лучше, чем все другие кривые (R-квадрат у него выше), однако его тренд после девятого периода меняется и стремится к сниже­нию. Поэтому выбор теоретической кривой зависит от эксперт­ного исследования.

Будем считать, что такой кривой является парабола, т.е. поли­ном второй степени. Хотя у параболы R-квадрат меньше, чем у поли­нома четвертой степени, однако он значительно выше по сравнению с другими кривыми.

Итак, выполняем экстраполяцию трех динамических рядов со сглаживанием их по параболе и прогнозированием на 10-й и 11-й пе­риоды. С помощью «Мастера функций» и встроенной функции «Тенденция» осуществляем прогноз трех динамических рядов в стро­ках 7:9 в клетки К7:К9 и L7:L9.

После того, как подготовлены прогнозные данные трех фактор­ных признаков на 10-й и 11-й периоды, осуществим прогноз уровня преступности на основе уравнения множественной регрессии. Для этого активизируем клетку В 10. Снова используя «Мастера функций», вызываем функцию «Тенденция» и заполняем в ее диалоговом окне необходимые параметры. Далее копируем получившуюся формулу из клетки В 10 в диапазон клеток С10:ЫО. Результаты представлены в табл. 3.8.12.

Сравнивая прогнозы уровня преступности на основе полинома четвертого порядка и уравнения множественной регрессии, убежда­емся в хорошем совпадении значений в ячейках L6 и L10 (195,9 и 196,1) в 11-м периоде (см. табл. 3.8.12).

Прогнозирование уровня преступности с лагом 1 и 2. При по­строении уравнения множественной регрессии с лагом 0 нам прихо­дилось прогнозировать факторные признаки, являющиеся перемен­ными в этом уравнении. Их экстраполяция в 10-й, 11-й периоды мо­жет привести к дополнительным ошибкам в прогнозе уровня пре­ступности.

Обойти этот шаг можно, если построить уравнение регрессии, включив в него признаки, которые проявят себя в 10-м и 11-м перио­дах. К ним относятся (см. табл. 3.8.11) доля городского населения (г=0,72, лаг 1), доля иммигрантов (г=0,89, лаг 2), доля наркоманов (г=0,73, лаг 2), плотность сотрудников УР (г=0,76, лаг 2). Дополним рабочий лист Excel 5.0 для Windows этими рядами, которые займут строки 12:15 (см. табл. 3.8.13).

Таблица 3.8.13 Построение уравнения множественной регрессии с лагами 1 и 2

A BCDEFGHI										J	К	L
12	Доля городского населения		0,8	0,805	0,807	0,81	0,81	0,815	0,82	0,83	0,84	0,864
13	Доля наркоманов			2	2,3	4,3	6	6,9	7,9	11,7	16,2	18,9
14	Доля иммигран­тов			16,2	16,4	15,1	16,6	19,1	21,1	22,3	23,3	22
15	Плотность сотруд­ников УР			2,2	2,23	2,36	2,3	2,3	2,21	2,2	2,3	2,4
16	Множественная регрессия			69,82	68,41	43,76	51,63	62,57	99,12	129,3	112,2	194,7

Отметим, что на основе планирования и экспертных оценок до­ля городского населения в 11-м периоде составит 0,864. Поэтому в

ячейку L12 введем число 0,864.

После этой подготовительной работы активизируем ячейку D16 и с помощью «Мастера функций» вызываем функцию «Тенденция» и в ее диалоговом окне заполняем необходимые строки, вводя в качестве переменных четыре динамических ряда, указанных в табл. 3.8.13. Далее копируем полученную формулу множественной регрессии из клетки D16 в диапазон клеток E16:L16. Результаты представлены в табл. 3.8.13. Сравним расчетные показатели уровня преступности, находящиеся в ячейках L6 (табл. 3.8.12) и L16 (табл. 3.8.13), они при­мерно совпадают (195,9 и 194,7).

Отметим, что расчетные коэффициенты уравнения множествен­ной регрессии Excel 5.0 не показывает, а только дает конечный ре­зультат Y.

Анализ руководителем ОВД прогнозных результатов. На основе полученного прогноза руководителю органа внутренних дел следует подумать, как воздействовать на факторы, которыми он может управ-

452

453

лять. В качестве иллюстрации рассмотрим показатель «плотность со­трудников УР (на 10 тыс. нас.)»в табл. 3.8.13. Каким должен быть этот показатель, чтобы уровень преступности в 11-м периоде равнялся 190?

Для этого в листе Excel 5.0 активизируем ячейку L16 и выпол­ним команду «Подбор параметра». В диалоговом окне команды «Подбор параметра» в первой строке «Установить в ячейке» окажется адрес клетки , а именно $L$16. В ней находится расчетная формула. Во вторую строку «Значение» нужно поставить желаемый для руково­дителя (в 11-м периоде) уровень преступности, например 190. В тре­тью строку «Изменяя ячейку» нужно поставить адрес клетки, где на­ходится признак «плотность сотрудников УР (на 10 тыс. чел.)», а именно $L$15, и нажать кнопку ОК.

В результате в диалоговом окне «Состояние подбора параметра» появится результат. Он одновременно будет находиться в ячейках L 15 и L16. Если подбор параметра руководителя удовлетворяет, то он для последующего принятия решения должен учесть, что обеспечение общего уровня преступности в расчете на 10 тыс. чел. (190) достига­ется при наличии плотности сотрудников УР на 10 тыс. чел. равной 2,417 (вместо 2,4).

Таким образом, программы различных методов статистического анализа, установленные на современных компьютерах, являются мощным средством повышения эффективности аналитической дея­тельности органов внутренних дел.

ВОПРОСЫ ДЛЯ КОНТРОЛЯ И САМОПРОВЕРКИ

1. Назовите три основных этапа статистической работы в органах внутренних дел.

2. Что понимается под статистическим наблюдением?

3. В чем сущность выборочного метода, используемого в сис­теме МВД России?

4. Перечислите виды группировок статистических данных.

5. Перечислите обобщающие показатели, используемые в ста­тистике системы МВД России.

6. Дайте характеристику средним величинам: средней арифмети­ческой, средневзвешенной, средней геометрической, моде, медиане. При­ведите примеры их использования в органах внутренних дел.

454

7. Дайте характеристику показателям вариации: размаху ва­риации, дисперсии, среднему квадратическому отклонению, коэффи­циенту вариации. Приведите примеры их использования в органах внутренних дел.

8. Что называется динамическим рядом? В чем разница между моментными и интервальными рядами? Приведите примеры их ис­пользования в органах внутренних дел.

9. Перечислите статистические показатели, количественно характеризующие динамические ряды?

10. В чем сущность корреляционного анализа? Что оценивает коэффициент корреляции? В чем сущность регрессионного анализа?

3.9. Системы календарного планирования, контроля и информационного обмена в компьютерных сетях

Слаженная работа органа внутренних дел во многом определя­ется эффективностью труда руководителя и его подчиненных и зави­сит от того, как распределено их рабочее время. Планирование рабо­чего времени и контроль за выполнением мероприятий приводят к экономии времени, поскольку самым важным фактором в деятельно­сти ОВД является именно временной фактор.

Непродуманное распределение времени руководителями на раз­личные виды работ дезорганизует работу исполнителей, не позволяя им четко планировать свое время, а это пагубно действует на процесс функционирования подразделения в целом.

При анализе работы руководителей органов внутренних дел бы­ло выявлено, что свой рабочий день, как правило, они не планируют и продолжительность их рабочего дня и недели значительно выше ус­тановленной.

Регламентировать распределение рабочего времени руководи­телей на выполнение различных работ можно с помощью распорядка рабочего дня. Он может быть индивидуальным и коллективным (для начальников подразделений). Нужно указывать время участия от­дельных руководителей в общих мероприятиях, согласованность про­водимой ими работы.

Индивидуальный распорядок рабочего дня начальников под­разделений ОВД и отдельных исполнителей должен строиться с уче­том распорядка дня руководителей верхней ступени управления. Вме-

455

• начальник ОВД (АРМ_10) устанавливает всем исполнителям одинаковый приоритет Modify;

• каждый исполнитель входит в расписание начальника коман­дой «Open Other's Appt Book» (Открыть другой ежедневник);
  
• каждый исполнитель находит свои задачи-мероприятия ко­мандой поиска. В диалоговом окне команды в позиции «Search for» (Найти) нужно ввести слово, например АРМ_5;
  
• исполнитель выделяет найденное мероприятие и выполняет команду копирования мероприятия. Затем он возвращается в свое расписание командой «Window-APM_5» (Окно-ежедневник АРМ_5);
  
• исполнитель в своем ежедневнике выделяет строку для встав­ки и выполняет команду вставки;
  
• если задач-мероприятий несколько, исполнитель снова входит в рас­писание начальника командой «Window-APM_10» и выполняет шаги 3-5.
  

Работа с программами электронной почты и расписания в сетях с другими операционными системами аналогична. Добавим, что сете­вые программы постоянно развиваются и совершенствуются.

Таким образом, работа сотрудников органов внутренних дел в вычислительных сетях позволяет оперативно решать целый комплекс современных задач, связанных с реализацией многочисленных функ­ций на качественно новом уровне.

ВОПРОСЫ ДЛЯ КОНТРОЛЯ И САМОПРОВЕРКИ

1. Что понимается под календарным планированием в органах внутренних дел?

2. Как осуществляются функции контроля в органах внутрен­них дел в отсутствие сети?

3. Перечислите основные задачи, решаемые в ЛВС. Как их ис­пользовать в работе органов внутренних дел?

4. Как работает всемирная компьютерная сеть Internet? Какова ее структура? Как ее использовать в работе системы МВД России?

5. Какие возможности для взаимодействия и контроля откры­вает руководителю органа внутренних дел программа-приложение «электронная почта «?

6. Как использовать сетевые папки сообщений электронной почты для учета и контроля в органе внутренних дел?

7. Как организовать совместную работу сотрудников органа внутренних дел с помощью сетевой программы «Расписание»?

498

Г л а в а 4. ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ В УПРАВЛЕНИИ ОРГАНАМИ ВНУТРЕННИХ ДЕЛ

4.1. Принципы применения информационных тех­нологий в деятельности органов внутренних дел

Анализ, изучение и овладение принципами построения и применения информационных технологий в деятельности ОВД не­разрывно связаны с изучением законов развития правоохранительных систем, а также закономерностей информации социального управле­ния.

Понятие закона выражает порядок необходимой и прочной свя­зи между явлениями или свойствами социальных объектов, их повто­ряющиеся существенные отношения, в том числе и такие, при кото­рых изменение одних явлений вызывает вполне определенное изме­нение других. Под закономерностью же следует понимать устойчи­вые, повторяющиеся связи и отношения между явлениями, опреде­ляющие объективные условия существования и развития того или иного социального процесса. Закономерность - это форма конкретно­го проявления объективного закона.

Детальное изучение законов и закономерностей управления ОВД предусмотрено академическими курсами по теории управления органами внутренних дел, организации управленческой деятельности в органах внутренних дел, управления органами внутренних дел в особых условиях и представлено в соответствующей учебной и учеб­но-методической литературе.

Что же касается законов и закономерностей информационно-технологического обеспечения управления ОВД, то следует учиты­вать недостаточную степень их исследовательности и изученности. Группа закономерностей построения и функционирования информа­ционных технологий управления, связанных с достижением его соци­альных целей, находится в настоящее время на стадии теоретического

499

осмысления и сопровождается интенсивными научно-практическими исследованиями.

Закономерности информационно-технологического обеспече­ния деятельности ОВД объективно следуют из группы закономерно­стей социального управления, связанных с реализацией организаци­онно-технологических целей управления. К группе объективных за­кономерностей информационно-технологического обеспечения в сфере правоохранительной деятельности относят:

1. Обусловленность организации информационных техноло­гий управления в сфере правоохранительной деятельности осо­бенностями объекта информационного обеспечения. Эта законо­мерность косвенно вытекает из закона необходимого разнообразия. В агрегированном виде объектом информационного обеспечения явля­ется система управления ОВД. При более детальном, предметном рас­смотрении круга объектов информационного обеспечения оказывает­ся, что их перечень на 1-2 порядка превышает соответствующий пе­речень объектов управления. Это связано с тем, что содержание ин­формационного обеспечения может относиться ко всему процессу управления, к определенным его функциям и стадиям, методам и формам, к деятельности отдельных управленческих звеньев, к кон­кретным видам управляемой правоохранительной деятельности, к деятельности конкретных категорий личного состава и отдельных сотрудников ОВД и военнослужащих ВВ. И в каждом из этих слу­чаев обеспечивающие информационные технологии будут характе­ризоваться своей спецификой и особенностями. Так, информаци­онно-технологическое обеспечение общеуправленческих функций системы ОВД дифференцируется на информационные технологии прогнозирования, планирования, организации, регулирования и контроля.

2. Непрерывность и цикличность информационно-техноло­гического обеспечения процесса управления в сфере правоохра­нительной деятельности. Эта объективная закономерность тесно связана с достаточно изученной закономерностью цикличности, не­прерывности процесса управления. Информационные технологии управления ОВД призваны обеспечивать ряд постоянно повторяю­щихся взаимосвязанных операций по сбору, хранению, обработке, передаче и представлению информации, что обеспечивает неразрыв­ность управленческих процедур во времени, цикличный переход от одной управленческой функции к другой.

500

3. Функциональная специализация информационных техно­логий управления ОВД, происходящая по мере усложнения сферы правоохранительной деятельности. Данная закономерность связана с динамикой социального развития и с особенностями прогресса ком­пьютерной индустрии. Традиционные общепринятые схемы инфор­мационного обеспечения сферы правопорядка в условиях реформи­руемого общества все чаще оказываются неэффективными и транс­формируются в специализированные подсистемы и комплексы. По­нимание этой закономерности позволит успешно решать вопросы со­отношения централизации и децентрализации информационно-технологического обеспечения ОВД, создания и функционирования информационных технологий, ориентированных на функциональную специфику решения неоднозначных управленческих задач в различ­ных регионах страны.

4. Технологический консерватизм информационного обес­печения правоохранительной деятельности в сравнении с дина­мичностью и изменчивостью процессов управления. Как следует из практики деятельности ОВД последних пяти-семи лет, сущест­вующие структуры информационно-технологического обеспечения неизбежно устаревают, при этом скорость старения характеризуется неизменным нарастанием. Очевидно, что технологические преобразо­вания должны быть адаптивны изменяющимся целям и соответст­вующим им функциям управления.

Объективные закономерности информационного обеспечения управления ОВД не исчерпываются приведенным кратким перечнем. Познание технических закономерностей - это процесс познания объ­ективной реальности развития общества с присущими ему противоре­чиями и сложностями.

Переходя к рассмотрению принципов построения и применения информационных технологий в деятельности ОВД, отметим, что они служат основой практической реализации объективных законов и за­кономерностей в процессе жизнедеятельности правоохранительных систем. Именно поэтому рассмотрению информационно-технических принципов управления всегда должен предшествовать анализ соот­ветствующих законов и закономерностей.

Под принципами информационно-технологического обеспе­чения управления ОВД следует понимать императивы, правила, по­стулаты и общие идеи о том, как должна строиться, функциониро­вать и развиваться система информационных технологий в сфере