Рабочая учебная программа по дисциплине 4 Задания на контрольные работы

Вид материала

Рабочая учебная программа

Содержание ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ 1 Поверхностные интегралы первого рода V функция и - гладкая поверхность S D представляет собой проекцию поверхности S D представляет собой проекцию поверхности S D в данном случае представляет собой прямоугольник ABCD 2. Поверхностные интегралы второго рода ЭЛЕМЕНТЫ ТЕОРИИ ПОЛЯ 1 Скалярные и векторные поля V задано скалярное поле M области пространства V Поверхностью уровня 2 Производная по направлению M и найдем скорость изменения функции поля U 3. Градиент скалярного поля 4 Поток векторного поля П>0, то жидкость вытекает из данного объема, и внутри замкнутой поверхности имеются источники поля. Если П 5. Дивергенция векторного поля 6. Теорема Остроградского – Гаусса 7. Циркуляция векторного поля L. Пример 8. Ротор векторного поля. Формула Стокса ... Полное содержание

Подобный материал:

• Рабочая программа, методические указания по выполнению курсовой работы и контрольные, 1000.11kb.
• Программа и контрольные задания по учебной дисциплине, 858.36kb.
• Программа и контрольные задания по учебной дисциплине «эконометрика» для студентов, 555.04kb.
• Рабочая программа методические указания контрольные задания для студентов специальности, 833.92kb.
• Программа и контрольные задания по учебной дисциплине «трудовое право» для студентов, 805.51kb.
• Программа и контрольные задания по учебной дисциплине «отечественная культура» для, 729.22kb.
• Рабочая программа По дисциплине «Стратегическое управление организацией» Для курса, 197.74kb.
• Программа и контрольные задания по учебной дисциплине «отечественная история» для студентов, 583.38kb.
• Программа, контрольные задания и тематика курсовых работ по учебной дисциплине основы, 557.3kb.
• Программа, методические указания и контрольные задания по дисциплине концепции современного, 717.75kb.

ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ

1 Поверхностные интегралы первого рода

Пусть - непрерывная в некоторой области пространства V функция и - гладкая поверхность S , где задана в некоторой области D плоскости xOy. Разобьем поверхность S на n частей , площади которых обозначим , а диаметры . В каждой части выберем произвольную точку и определим значение функции F в этих точках. Далее составим интегральную сумму .

Определение. Если при интегральная сумма имеет предел, то он называется поверхностным интегралом первого рода от функции по поверхности S и обозначается .

(1)

Теорема. Если поверхность S гладкая, т.е. такая, что в каждой ее точке существует касательная плоскость, которая непрерывно меняется с перемещением точки касания по поверхности, а функция непрерывна на этой поверхности, то для функции существует поверхностный интеграл первого рода.

Свойства поверхностного интеграла первого рода

Поверхностные интегралы первого рода обладают следующими свойствами:

1. S – площадь поверхности.

2.

3.

4. Если поверхность разбита на части S₁ и S₂, такие что , то



5. Если , то



6. .

Вычисление поверхностных интегралов первого рода зависит от способа задания поверхности

Пусть поверхность S задана функцией . Тогда соответствующий поверхностный интеграл первого рода вычисляется по формуле

, (2)

где D представляет собой проекцию поверхности S на плоскость xOy.

Если поверхность S задана уравнением вида , то для вычисления поверхностного интеграла первого рода используется формула

, (3)

где D представляет собой проекцию поверхности S на плоскость xOz.

Аналогично для случая , используется формула

, (4)

где D представляет собой проекцию поверхности S на плоскость yOz.

Пример 4. Вычислить , где S – часть цилиндрической поверхности , отсеченной плоскостями z=0, z=2.

Решение. Воспользуемся формулой (4). Поверхность D в данном случае представляет собой прямоугольник ABCD c вершинами в точках с координатами (0;-1;0), (0;1;0), (0;1;2), (0;-1;2).

Вычислим: , следовательно,

2. Поверхностные интегралы второго рода

Если на поверхности S есть хотя бы одна точка и хотя бы один не пересекающий границу поверхности контур, при обходе по которому направление нормали в точке меняется на противоположное, то такая поверхность называется односторонней.

Если при этих условиях направление нормали не меняется, то поверхность называется двухсторонней.

За положительное направление обхода контура L, принадлежащего поверхности, будем считать такое направление, при движении по которому по выбранной стороне поверхности сама поверхность остается слева.

Двухсторонняя поверхность с установленным положительным направлением обхода называется ориентированной поверхностью.

Рассмотрим в пространстве XYZ ограниченную двухстороннюю поверхность S, на которой определена функция. Произвольно выбранную сторону поверхности разбиваем на n частей и проектируем их на координатные плоскости. При этом площадь проекции ,, берем со знаком «+», если нормаль к выбранной стороне поверхности составляет с осью Oz острый угол, и со знаком «-», если этот угол тупой. Составляем интегральную сумму, которая имеет вид

(5)


Определение. Если при стремлении к нулю шага разбиения поверхности S интегральные суммы имеют конечный предел, то этот предел называется поверхностным интегралом второго рода и обозначается

(6)

аналогичным образом определяются поверхностные интегралы по проекциям на две другие координатные плоскости. Таким образом:







Общим видом поверхностного интеграла второго рода служит интеграл

(7)

Свойства поверхностного интеграла второго рода

1. Поверхностный интеграл второго рода изменяет знак при перемене стороны поверхности.

2. Постоянный множитель можно выносить за знак интеграла.

3. Поверхностный интеграл второго род от суммы двух функций равен сумме соответствующих интегралов от каждой функции.

4. Поверхностный интеграл второго рода о всей поверхности равен сумме соответствующих интегралов по всем частям, эту поверхность составляющим.

Вычисление поверхностного интеграла второго рода сводится к вычислению двойных интегралов.

Пусть поверхность S задана уравнением . Обозначим проекции этой поверхности на координатные плоскости как . Тогда

(8)

Замечание. Можно показать справедливость равенств

(9)

где ds – элемент площади поверхности, - направляющие косинусы нормали к выбранной поверхности. Если поверхность задана уравнением , то направляющие косинусы определяются соотношениями

(10)

Поверхностные интегралы первого и второго рода связаны соотношением

. (11)

ЭЛЕМЕНТЫ ТЕОРИИ ПОЛЯ

1 Скалярные и векторные поля

Полем называется область V пространства, в каждой точке которой определено значение некоторой величины.

Если в каждой точке M области пространства V поставлена в соответствие скалярная величина , то говорят, что в области V задано скалярное поле.

Примерами скалярных полей можно считать поле температур, поле атмосферного давления, поле электрического потенциала, и т.д.

Если в каждой точке M области пространства V поставлена в соответствие векторная величина , то говорят, что в области V задано векторное поле.

Примерами векторных полей являются электромагнитное поле, поле силы тяжести, поле плотности электрического тока и т.д.

Скалярное поле в пространстве трех измерений задается функцией трех переменных . Для наглядного представления скалярного поля используют поверхности уровня.

Поверхностью уровня скалярного поля называется геометрическое место точек, в которых функция принимает постоянное значение, т.е.

(1)

Через каждую точку поля проходит только одна поверхность уровня. Поверхности уровня могут вырождаться в линии уровня и точки.

Векторное поле в трехмерном пространстве задается векторной функцией

(2)

Характеристиками векторного поля являются векторные линии.

Векторной линией поля называется линия, направление касательной к которой в каждой ее(линии) точке совпадает с направлением вектора .

Для векторного поля (2) векторные линии описываются системой дифференциальных уравнений

(3)

Для характеристики скалярного поля вводятся понятия производной по направлению и градиента, а для характеристики векторного поля – понятия дивергенции, ротора, циркуляции и потока поля.

2 Производная по направлению

Пусть в пространстве задано поле . Выберем в этом пространстве некоторую точку M и найдем скорость изменения функции поля U при движении точки M в направлении вектора . Пусть вектор имеет направляющие косинусы . Напомним, что если вектор задан своими координатами: , то его направляющие косинусы вычисляются по формулам

(3)

Определим приращение функции , возникающие при переходе от точки M к точке вдоль вектора как .

Производной функции по направлению вектора в точке M называется предел

. (4)

Производная по направлению представляет собой мгновенную скорость изменения поля в точке вдоль направления и характеризует скорость изменения поля в точке M по заданному направлению: если >0, то функция поля возрастает в направлении вектора , а если <0, то функция поля убывает.

Формула для вычисления производной по направлению имеет вид

(5)

Пример 5. Задано скалярное поле . Найти скорость изменения поля в точке в направлении вектора .

Решение. Найдем направляющие косинусы вектора :

.

Найдем частные производные функции U:



Вычислим значения частных производных в точке :



По формуле (5) получим



Поскольку <0, то функция поля в данной точке в заданном направлении убывает со скоростью

Ответ: =

3. Градиент скалярного поля

Градиентом скалярного поля называется вектор, направленный в сторону наиболее быстрого изменения функции поля, причем модуль этого вектора численно равен производной функции поля в направлении градиента.

Градиент скалярного поля U(M) = U(x,y,z) определяется соотношением


. (6)

В математической теории поля широко используют символическое выражение, обозначаемое ("набла"): , напоминающее по форме вектор, разложенный по базисным ортам , где вместо координат вектора записаны операторы дифференцирования . Это выражение называют векторным дифференциальным оператором или оператором Гамильтона. В обозначениях оператора Гамильтона соотношение (31) можно записать в виде

. (7)

Производная функции поля по направлению и градиент связаны соотношением

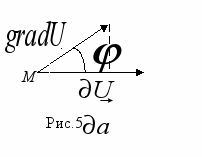
(8)

где – угол между векторами и и

. (9)

Т.о. наибольшая скорость изменения функции поля равна (при условии, что градиент сонаправлен с вектором и ) и определяется по формуле (9).

Градиент скалярного поля в заданной точке направлен по нормали к поверхности уровня, проходящей через эту точку.

Пример 6. Найти наибольшую скорость возрастания функции поля в точке .

Решение. Найдем :

,

тогда

,

и наибольшая скорость возрастания функции равна

.

Ответ:

4 Поток векторного поля

Пусть векторное поле задано в пространстве вектором (26).

Потоком векторного поля через поверхность S в сторону, определяемую направлением нормали к этой поверхности, называется интеграл по поверхности от скалярного произведения вектора поля на единичный вектор нормали к этой поверхности

, (10)

где единичный вектор нормали определяется направляющими косинусами():

. (11)

Так как , , то (10) можно записать в виде

. (12)

Пусть поверхность S задана уравнением .Тогда используя взаимосвязь поверхностных интегралов первого и второго рода , выражение (12) можно записать в виде

(13)

где знаки перед слагаемыми определяются знаками направляющих косинусов, а проекции поверхности S на координатные плоскости.

Поток вектора – скалярная величина. Если рассматривать поле скоростей движущейся жидкости, то величина потока П равна объему жидкости, протекающей через поверхность S за единицу времени.

В случае замкнутой поверхности, ограничивающей некоторый объем V, поток вектора записывается в виде

. (14)

В этом случае вектор представляет собой нормаль к внешней поверхности, и говорят о потоке изнутри поверхности.

Так, если П>0, то жидкость вытекает из данного объема, и внутри замкнутой поверхности имеются источники поля. Если П<0, то жидкость в данный объем втекает, и в замкнутой поверхности имеются «стоки». В случае, когда П=0, то за единицу времени количество вытекающей жидкости равно количеству втекающей, и внутри замкнутой поверхности источников и стоков у поля нет.

Пример 7 (типовая задача контрольной работы) Найти поток векторного поля в направлении нормали через поверхность S треугольника, высекаемого координатными плоскостями из плоскости, проходящей через точку перпендикулярно вектору . Сделать чертеж.

Решение. Для вычисления потока воспользуемся формулой (13)

1. Составим уравнение плоскости, в которой лежит искомый треугольник. Эта плоскость проходит через точку перпендикулярно вектору . Уравнение такой плоскости имеет вид:

.

В нашем случае



или

(15)

Следовательно, поверхность S является частью плоскости Запишем это уравнение в отрезках:

. (16)

Отсюда, отрезки координатных осей, отсекаемые плоскостью (15) от начала координат, равны: . Построим поверхность S.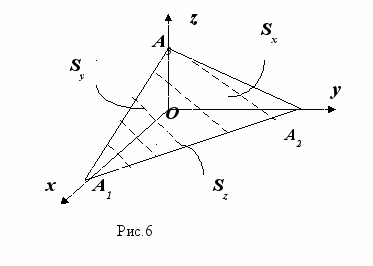



2. Найдем границы областей Из уравнения плоскости(15) получаем



Найдем уравнения сторон треугольника :

. Уравнение этой стороны найдем из уравнения (16) при условии, что.

, откуда .

. Уравнение этой стороны найдем из уравнения (16) при условии, что.

, откуда .

. Уравнение этой стороны найдем из уравнения (16) при условии, что.

, откуда .

Тогда области имеют параметры:



3. Для определения знаков перед слагаемыми в формуле (13), найдем направляющие косинусы единичного вектора нормали .



Полученные значения направляющих косинусов – положительные, значит, перед всеми слагаемыми в формуле (13) ставим знак «+».

4. Векторное поле в нашем случае имеет вид , поэтому



Тогда поток векторного поля определяется по формуле (13):



Ответ: П=16

5. Дивергенция векторного поля

Дивергенцией векторного поля



в точке M называется скалярная величина вида

(17)

Дивергенция - скалярная величина, которая характеризует плотность распределения источников векторного поля. Если в точке M , то точка представляет собой источник поля (например, положительный заряд в случае электростатического поля); если в точке M , то в этой точке находится «сток» поля (отрицательный заряд в случае электростатического поля). Если в каждой точке поля , то поле не имеет источников и называется соленоидальным (например, магнитное поле).

Пример 8. Вычислить дивергенцию векторного поля в точке .

Решение. В общем виде векторное поле задается вектором (1). В нашем случае

,

тогда





Ответ: =3.

6. Теорема Остроградского – Гаусса

Формула Остроградского - Гаусса связывает поверхностный интеграл второго рода по замкнутой поверхности с тройным интегралом по пространственной области, ограниченной этой поверхностью.

Пусть функции непрерывны вместе со своими частными производными первого порядка в области пространств V, ограниченной поверхностью S. Имеет место формула:

(18)

Эта формула называется формулой Остроградского-Гаусса.

Левая часть формулы представляет собой поток вектора через замкнутую поверхность S, а подынтегральная функция в правой части представляет собой дивергенцию вектора . Таким образом, формулу (18) можно переписать в виде:

(19)

т.е. интеграл от дивергенции векторного поля по объему равен потоку вектора через поверхность, ограничивающую этот объем.

Пример 9. Пользуясь формулой Остроградского-Гаусса, вычислить поток векторного поля через полную поверхность конуса .

Решение. Найдем дивергенцию векторного поля:

.

Тогда

.

Переходя к сферическим координатам, получим:

.

Ответ: .

7. Циркуляция векторного поля

Пусть векторное поле задано в области V вектором (1). Выберем в этой области некоторую замкнутую ориентированную кривую L. На этой кривой выберем произвольную точку . Пусть - радиус-вектор этой точки. Тогда вектор направлен по касательной к кривой L в направлении ее обхода.

Криволинейный интеграл по замкнутому контуру L от скалярного произведения вектора на вектор , касательный к контуру L, называется циркуляцией векторного поля вдоль замкнутой кривой L.

. (20)

Т.к. , то выражение для циркуляции можно переписать в виде

, (21)

или т.к. и , то

. (22)

Физический смысл циркуляции заключается в следующем:

если - поле силы, то циркуляция вектора представляет собой работу силы при перемещении материальной точки вдоль замкнутой кривой L.

Пример 10. Вычислить циркуляцию плоского векторного поля вдоль кривой x=3cost, y=sint с обходом по часовой стрелке.

Решение. Данная кривая представляет собой эллипс. Обход кривой совершается по часовой стрелке, поэтому t меняется от 2 до 0.





Следовательно, циркуляция вычисляется следующим образом: .

Ответ: Ц=0.

8. Ротор векторного поля. Формула Стокса

Формула Стокса устанавливает связь между поверхностными и криволинейными интегралами второго рода.

Пусть функции непрерывны вместе со своими частными производными первого порядка в точках ориентированной поверхности S. И пусть L – граница поверхности S. Имеет место формула:

(23)

(интегрирование вдоль кривой L производится в положительном направлении, т.е. при обходе границы L поверхность S должна все время оставаться слева).

Формула (23) называется формулой Стокса.

Заметим, что интеграл в правой части выражения (23) представляет собой циркуляцию вектора вдоль замкнутой кривой L.

Ротором векторного поля, задаваемого вектором (1) в точке M, называется вектор

(24)

Данную формулу можно переписать в виде

(25)

Тогда левая часть формулы (23) представляет собой поток вектора ротора через поверхность S, ограниченную контуром L и формулу Стокса можно переписать в виде

. (26)

Т.е. циркуляция векторного поля вдоль замкнутого контура L равна потоку ротора вектора через поверхность S, лежащую в поле этого вектора и ограниченную контуром L.

Направление ротора – это направление, вокруг которого циркуляция имеет наибольшее значение по сравнению с циркуляцией вокруг любого другого направления.

В поле скоростей вращающегося тела ротор характеризует угловую скорость вращения (с точностью до числового множителя).

Пример 11. Вычислить циркуляцию вектора вдоль окружности x²+y²=1, z=0 в положительном направлении.

Решение. В этом случае Следовательно,



по формуле Стокса



Ответ: Ц=.

Пример12. Вычислить ротор векторного поля: = y²- x² +z².

Решение.

.

Ответ: .

9. Классификация векторных полей

1. Соленоидальное поле
   

Векторное поле называется соленоидальным, если в каждой его точке дивергенция поля равна нулю, т.е. .

Примерами соленоидальных полей являются магнитное поле, поле скоростей вращающегося тела и т.д.

Свойства соленоидального поля

1. Поток вектора поля через любую замкнутую поверхность равен нулю.
   
2. Соленоидальное поле является ротором некоторого вектора, т.е. если , то существует другое поле , для которого .
   
3. В соленоидальном поле поток вектора через поперечное сечение векторной трубки сохраняет постоянное значение.
   

2. Потенциальное поле
   

Векторное поле называется потенциальным, если во всех точках поля ротор вектора поля равен нулю, т.е. .

Одним из примеров потенциального поля является электростатическое поле напряженности точечных зарядов.

Свойства потенциального поля

1. Циркуляция потенциального поля по любому замкнутому контуру в этом поле равна нулю.
   
2. В потенциальном поле криволинейные интегралы вдоль всех кривых, имеющих общие начала и концы имеют одинаковые значения (криволинейный интеграл не зависит от формы кривой).
   
3. Потенциальное поле является полем градиента некоторой скалярной функции, т.е.
   

Такую функцию называют потенциалом векторного поля .

Потенциал векторного поля может быть найден по формуле

(27)

где – координаты фиксированной точки, а – координаты произвольной точки.

Пример 13 (типовая задача контрольной работы). Проверить, является ли векторное поле потенциальным и соленоидальным? В случае потенциальности поля найти его потенциал.

Решение. Вектор имеет координаты . В нашем случае



1. Проверим, является ли поле соленоидальным. Для этого найдем :

,

следовательно, поле не является соленоидальным.

2. Проверим, является ли поле потенциальным .Для этого вычислим :



следовательно, векторное поле является потенциальным.

3. Найдем потенциал поля, воспользовавшись формулой (27). Пусть - фиксированная точка. Тогда





где – постоянная, .

Ответ: поле потенциально и не соленоидально, потенциал поля где .

ЭЛЕМЕНТЫ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ

1. Основные определения

Введем некоторые вспомогательные определения.

Пусть задана функция действительного аргумента, принимающая комплексные значения. Она называется оригиналом, если удовлетворяются следующие три условия:

1. функция определена на всей числовой оси и кусочно-непрерывна, т.е. на всяком конечном интервале имеет конечное число точек разрыва первого рода;
   
2. если , то ;
   
3. имеет ограниченный рост, т.е. возрастает не быстрее показательной функции: существуют такие постоянные М  >  0 и , что при t>0.
   

Величина ( – нижняя грань всех чисел ) называется показателем роста функции . Для любой ограниченной функции, являющейся оригиналом можно принять =0. Совокупность всех оригиналов называется пространством оригиналов.

Каждому оригиналу ставится в соответствие его изображение

_{F(p) = (1)}

Здесь p = a+b – комплексное переменное. Интеграл в правой части формулы (1) носит название интеграла Лапласа.

Переход, определяющий изображение по оригиналу , называется преобразованием Лапласа.

Обычно оригиналы обозначаются строчными буквами, а их изображения – соответствующими заглавными буквами. Тот факт, что есть изображение , символически записывают так: или .

Совокупность всех изображений называется пространством изображений.

Закон соответствия и классы оригиналов и изображений выбраны таким образом, что некоторым операциям над оригиналами соответствуют более простые операции над изображениями. В частности, линейное дифференциальное уравнение после преобразования по Лапласу переходит в алгебраическое уравнение, которое легко решается. Переходя затем от изображений к оригиналам, можно найти решение дифференциального уравнения.

2. Свойства преобразования Лапласа

1. Теорема 1 (теорема линейности). Для любых комплексных постоянных и

₍₂₎

(здесь и всюду в дальнейшем считаем , ).

2. Теорема 2 (теорема подобия). Для любого постоянного

_{. (3)}

3. Дифференцирование оригинала. Если функции, , …, являются функциями – оригиналами и , то

,

,

……………………………………….

,

где под (к=1,2,..,n-1) понимаем .

4. Дифференцирование изображения. Дифференцирование изображения сводится к умножению на (–t) оригинала

₍₄₎

или, вообще

_{. (5)}

5. Интегрирование оригинала. Интегрирование оригинала сводится к делению изображения на р, т.е. если , то

_{. (6)}

6. Интегрирование изображения. Если интеграл сходится, то он служит изображением функции :

. (7)

7. Теорема 3 (теорема смещения). Если , то для любого комплексного

_{. (8)}

8. Теорема 4 (теорема запаздывания). Если , то для любого положительного

_{. (9)}

9. Теорема 5 (теорема о свертке). Произведение двух изображений и также является изображением, причем

_{. (10)}

Интеграл в правой части формулы называется сверткой функции и , и обозначается символом *.

10 Теорема 6 (первая теорема разложения). Если – аналитическая функция в окрестности бесконечно удаленной точки и равна в ней нулю и если лорановское разложение в окрестности бесконечно удаленной точки имеет вид =, то оригиналом служит функция

_{=. (11)}

Причем этот ряд сходится при всех t.

11. Теорема 7 (теорема единственности). Преобразование Лапласа F(p)= единственно в том смысле, что две функции и , имеющие одинаковые преобразования Лапласа, совпадают во всех точках непрерывности для всех .