Рабочая учебная программа по дисциплине 4 Задания на контрольные работы

Вид материала

Рабочая учебная программа

Содержание 3. Криволинейные интегралы второго рода L замкнута, то на ней выбирается произвольная точка, которая принимается за конечные точки А L определены две функции P М вдоль ориентированной кривой L L задана параметрическими уравнениями x = L: если ориентации кривой L L задана явно уравнением y=f L, аналогично (10). Пусть кривая L

Подобный материал:

• Рабочая программа, методические указания по выполнению курсовой работы и контрольные, 1000.11kb.
• Программа и контрольные задания по учебной дисциплине, 858.36kb.
• Программа и контрольные задания по учебной дисциплине «эконометрика» для студентов, 555.04kb.
• Рабочая программа методические указания контрольные задания для студентов специальности, 833.92kb.
• Программа и контрольные задания по учебной дисциплине «трудовое право» для студентов, 805.51kb.
• Программа и контрольные задания по учебной дисциплине «отечественная культура» для, 729.22kb.
• Рабочая программа По дисциплине «Стратегическое управление организацией» Для курса, 197.74kb.
• Программа и контрольные задания по учебной дисциплине «отечественная история» для студентов, 583.38kb.
• Программа, контрольные задания и тематика курсовых работ по учебной дисциплине основы, 557.3kb.
• Программа, методические указания и контрольные задания по дисциплине концепции современного, 717.75kb.

3. Криволинейные интегралы второго рода

Рассмотрим ориентированную незамкнутую кривую L = АВ в плоскости хОу с началом в точке А и концом в точке В. Пусть P (x,y)  функция, определенная на кривой L. Разобьем кривую L последовательно точками А₀=А, А₁, А₂, . . . , А_n=В на дуги ₁= А₀А₁, ₂= А₁А₂, . . . , _n= А_n-1А_n . На каждой дуге _i выберем произвольную точку М_i(t_i , s_i) (i = 1, 2, . . . , n) (рис. 4).

Обозначим за x_i = x_i  x_i1 , y_i = y_i  y_i1, а за  наибольшую из длин дуг _i (i = 1,2, . . . , n).

Составим интегральную сумму функции P(x,y) вдоль кривой L относительно х



Определение. Предел , если он существует, называется криволинейным интегралом 2-го рода от функции P (x,y) вдоль кривой L относительно х и обозначается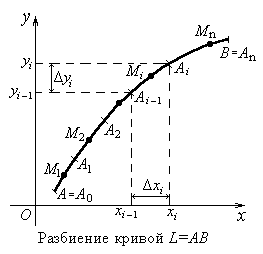





Рис. 4
(5)

Если кривая L замкнута, то на ней выбирается произвольная точка, которая принимается за конечные точки А и В, и криволинейный интеграл 2-го рода определяется аналогично случаю незамкнутой кривой.

Теорема (достаточное условие существования криволинейного интеграла второго рода). Если функция P(x,y) непрерывна и ограничена на L, то криволинейный интеграл 2-го рода вида (5) существует.

Свойства криволинейного интеграла 2-го рода

1. Криволинейный интеграл при изменении направления кривой меняет знак.



2.

3.

4.

Криволинейный интеграл 2-го рода от функции Q(x,y) вдоль кривой L относительно у определяется аналогичным образом как предел интегральных сумм

, (6)

где .

Пусть на кусочно-гладкой ориентированной кривой L определены две функции P(x, y) и Q(x, y). Тогда сумма интегралов (5) и (6) называется общим криволинейным интегралом 2-го рода от функций P (x,y) и Q (x,y) вдоль кривой L и обозначается

(7)

Физический смысл криволинейного интеграла 2-го рода.

Пусть  сила, действующая на материальной точку М(x,y), расположенную на ориентированной кривой L. Тогда работа, совершаемая силой при перемещении точки М вдоль ориентированной кривой L, равна

(8)

Замечание. Криволинейный интеграл 2-го рода аналогично определяется и для пространственной ориентированной кривой.

Площадь плоской фигуры. Пусть простая замкнутая кривая L ориентирована против часовой стрелки, D  область, ограниченная кривой L. Тогда площадь области D равна

(9)


Вычисление криволинейных интегралов второго рода также зависит от способа задания кривой.

Пусть ориентированная кривая L задана параметрическими уравнениями

x =  (t), y= (t),  ≤ t ≤,

где  (t),  (t)  непрерывно дифференцируемые на отрезке [,  ] функции. Тогда

. (10)

Пределы интегрирования выбираются в соответствии с ориентацией кривой L: если ориентации кривой L соответствует изменение параметра t от  до , то в формуле (10) выбирается первый вариант пределов интегрирования. В противном случае в (10) нужно выбирать вариант пределов интегрирования в скобках.

Пусть кривая L задана явно уравнением y=f(x), a≤ x ≤b, где f (x)  непрерывно дифференцируемая на отрезке [a, b] функция. Тогда

. (11)

Пределы интегрирования выбираются в соответствии с ориентацией кривой L, аналогично (10).

Пусть кривая L задана явно уравнением x=h(y), a≤ y ≤b, где h (y)  непрерывно дифференцируемая на отрезке [a, b] функция. Тогда

. (12)

Пределы интегрирования выбираются в соответствии с ориентацией кривой L, аналогично (10).

Пример 2. Вычислить , где кривая ОА задана на рис. 3.

Решение. Кривая ОА задается уравнением Положим ,

и применим формулу (11), при этом учитывая тот факт, что при движении по кривой от точки О до А переменная x меняется от 0 до 4.



Пример 3.

Вычислить где L  замкнутая кривая ОВАО из рис. 3.

Решение. Кривая L состоит из линий ОВ, ВА и АО. По свойству аддитивности криволинейного интеграла второго рода

. (13)

Отрезок ОВ задается уравнением у = 0 при 0 ≤ х ≤ 4. Значит, dy = 0.Тогда по формуле (11)

.

Отрезок ВA задается уравнением х = 4 при 0 ≤ у ≤ 4. Тогда dх = 0 и по формуле (12) имеем

.

Кривая АО задается уравнением при изменении значения у от 4 до 0. Значит, и по формуле (12) получаем

.

Подставляя вычисленные интегралы в (13), получим