Экономическая цикломатика: теория, методология, практика 08. 00. 13 Математические и инструментальные методы экономики

Вид материала

Автореферат

Содержание Во втором разделе В третьем разделе В четвёртом разделе В пятом разделе

Подобный материал:

• Математические методы анализа и оценки финансово-экономической деятельности предприятия:, 825.67kb.
• Программа вступительного экзамена по специальности 08. 00. 13 «Математические и инструментальные, 555.96kb.
• Рефератов по специальности 08. 00. 13 «Математические и инструментальные методы экономики», 114.15kb.
• Реферата по специальности 08. 00. 13 «Математические и инструментальные методы экономики», 141.02kb.
• Многоуровневые модели зависимости экономического роста от инвестиций: эконометрический, 321.8kb.
• Инструментарий анализа качества ассортимента и оценки рейтингов товаров предприятий, 286.28kb.
• Программа вступительного испытания по предмету «Экономическая теория», 103.39kb.
• Рабочая программа дисциплины «теория и методы принятия решений», 81.57kb.
• Рабочая программа дисциплины «методология исследования экономических систем», 59.68kb.
• Рабочая программа дисциплины «экономико-математические методы и модели», 129.59kb.

Во втором разделе ««Кусочная» концепция исследования экономической конъюнктуры» в результате системных исследований по анализу и поиску циклов в экономике было показано, как мало внимания обращается на тот очевидный факт, что в поведении самореорганизующейся экономики России и её отдельных регионов существуют периоды относительно стабильных политических, правовых, налоговых, таможенных и т.п. законов, правил, тарифов, положений, квот, отчислений, преференций и пр., сменяемых, правда, достаточно неожиданно и часто. Для верификации формального (трендового, детерминированного) анализа, поиска циклов, визуализации и прогнозирования важен тип исследуемого экономического процесса. При одних наборах экзогенных условий процесс может показать экспоненциальный рост, при смене их динамика экономического показателя может стать линейно-падающей и т.д. Чтобы собрать статистику поведения экономических показателей и продолжить её в прогнозном построении, требуется сделать отчётный период достаточно долгим. На длинном периоде увеличивается вероятность изменениях внешних условий, период неизбежно делится на отдельные «куски», внутри которых тип экономического поведения может кардинально меняться. Поэтому особую актуальность в экономике приобретает выбор унифицированной модельной системы. Эта универсальная система функций должна хорошо интерполировать и экстраполировать все виды типичных экономических процессов, автоматически «приспосабливаясь» своими фрагментами к их сезонности, структурным скачкам, асимптотичности, экспоненциальности, цикличности, хаотичности и пр.

В связи с этим в исследовании предлагается использовать «кусочную» концепцию на аппроксимационной базе. Из кусочно-полино- миальных функций мы остановили свой выбор на сплайнах со сплайновым представлением интерполяционной кривой на дискретном множестве точек, сплайн-моделированием, сплайн-анализом и сплайн-визуализацией на фазовых портретах, параметрических картинах взаимозависимостей, со сплайн-прогнозированием. Отличительная особенность сплайнов – они состоят из отрезков степенного полинома малого порядка, которые сходятся и «сшиваются» в заданных узловых точках «решётчатой» экономической функции.

Кусочно-полиномиальные функции универсальны как в том, что используются единообразно для сплайн-моделирования, фазового сплайн-анализа, сплайн-визуализации, так и для сплайн-прогнозиро-вания экономического поведения, когда его временной класс меняется на протяжении отчётного периода. Кусочно-полиномиальные методы также универсально применяются в экономических, производственных, финансовых и маркетинговых задачах, заменяя спектр систем аппроксимирующих многочленов. Классики (Дж. Алберг, Дж. Уолш, Э. Нильсон) недаром говорили о «подвижности и гибкости сплайнов».

Математический сплайн q–го порядка непрерывен и имеет (q-1) непрерывную производную, q–я производная претерпевает в точках соединения (узловых точках, узлах «сетки» или просто «узлах») разрыв с конечным скачком. Более двух десятков замечательных свойств выделяют сплайны из всего множества аппроксимирующих функций.

В моделировании и анализе в полной мере используется известное применение сплайнов при построении интерполяционных кривых на дискретном множестве точек – spline-smoothing, «сплайн-сглаживание». Строящаяся непрерывная сплайн-кривая становится действительно «гладкой», так сплайны визуально демонстрируют одновременно и периодичность, и «гладкость» процесса (рис. 4).

Математическая «сшивка» фрагментов сплайн-функции оптимально осуществляется значениями самой функции S_D(Y;X_j – 0) = S_D(Y;X_j + 0) = Y_j, значениями её производных S’_D(Y;X_j – 0) = S’_D(Y;X_j + 0), S”_D(Y;X_j – 0) = S”_D(Y;X_j + 0) .. слева и справа в узловых точках {áX_j, Y_jñ} (j = 1..N), так что S_D(Y;X), S’_D(Y;X), S”_D(Y;X) .. становятся непрерывными функциями во всей сетке X₁, .., X_N. Такая структура помогает выстраивать «кусочный» сплайн в единый аппроксимирующий ансамбль.

Из всех рассмотренных сплайн-систем в работе чаще используются кубические сплайн-функции или сплайны третьего порядка, предпочтение основывается на их исследованных и доказанных преимуществах. У кубических сплайн-функций S_D(Y;X) » f(X) свойство сплайнов, которое при поиске классов подходящих полиномов мы называем «внутренней оптимальностью», выражается теоремой Холлидея, утверждающей, что кубическое сплайн-построение минимизирует интеграл: 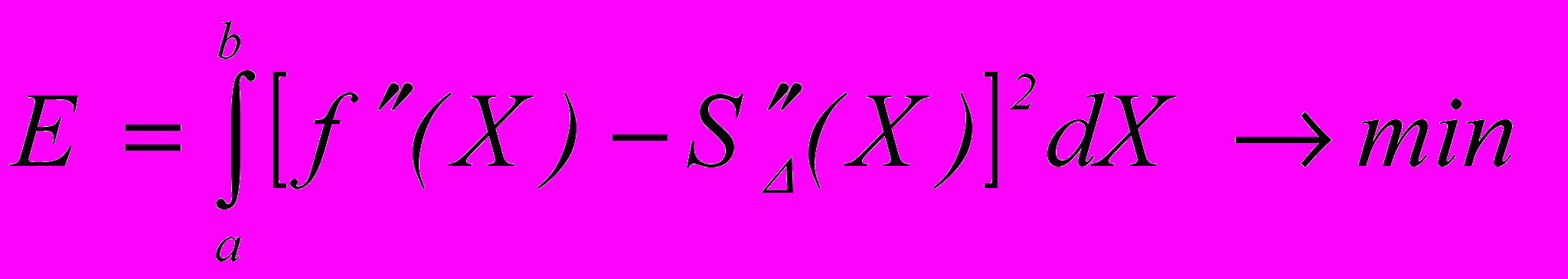. Это свойство кубического сплайна называется свойством наилучшего приближения, минимальной кривизны или нормы, именно оно лучше всего сохраняет статистическую «историю» процесса при переносе её в горизонт прогноза.

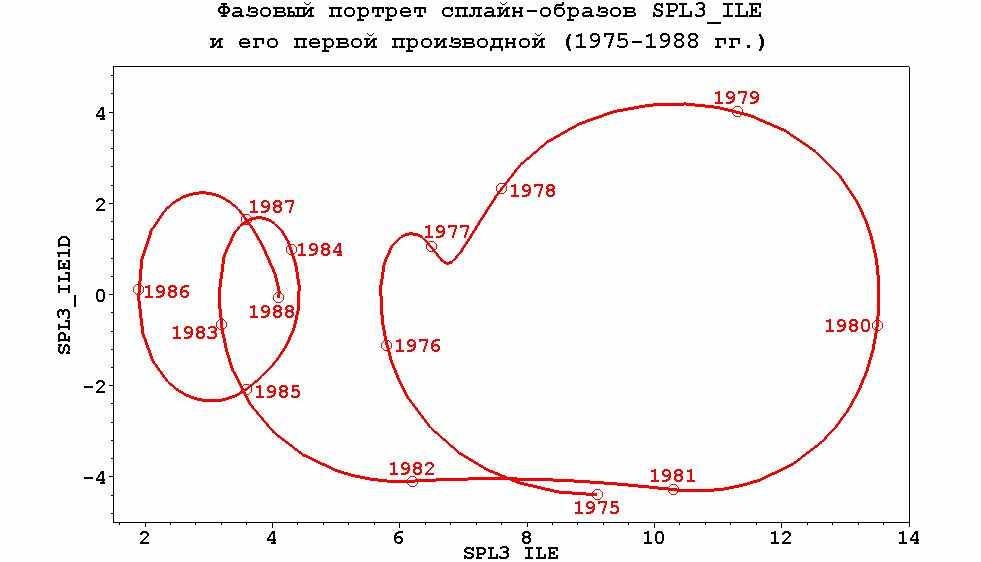Рисунок 6 - Фазовый портрет сплайн-образов уровня инфляции SPL3_ILE и его первой производной SPL3_ILE1D в американской экономике в 1975-1988 гг. («поросёнок»). «Большая инфляционная спираль» в 1975-1982 гг. и «малая» в 1982-1988 гг. Р. Рейган пришёл к власти в ноябре 1980 г. «Рейганомика» визуально характеризуется переходом от «большой» к «малой» спиралям, она свела годовую инфляцию от ~14% к 2-4%

Сплайны имеют инвариантную внутреннюю структуру, универсальную математическую форму, это свойство «фракталоподобия» сплайнов, самоподобия его «кусков» при аналитическом однообразии позволяет представлять их однотипно и экономно, используя в полной мере аналитические возможности систем компьютерной математики.

При общем универсализме сплайновых моделей значительно выигрывает моделирование ими сезонных и циклических процессов. Линейное слагаемое сплайна моделирует линейный тренд, а при знакопеременных последовательно следующих «моментах» сплайна его квадратичные и кубичные параболические слагаемые на перемежающихся участках становятся выпуклыми то «вверх», то «вниз», как бы «кусочно-периодическими», моделируя таким образом сезонную или циклическую составляющую экономического процесса. Впервые периодическое экономическое поведение достаточно точно удаётся моделировать степенными многочленами низкого порядка. Кусочно-полиномиальные многочлены заменили собой громоздкие гармонические многочлены и ряды Фурье, громоздкое и малопонятное экономисту сочетание трендового, сезонного и циклического поведения удаётся анализировать и прогнозировать единой сплайн-технологией.

Принципиальное отличие сплайн-подходов от классических эконометрических состоит в том, что регрессионные эконометрические построения теряют значение параметра (времени), при котором они получены, в то время как сплайн-построения сохраняют временной показатель каждого дискретного отсчёта, что существенно сказывается на точности последующего перехода к построению прогноза.

Сплайн-подход обогащает эконометрику. Теперь после замены решётчатых функций исходного экономического процесса сплайн-функциями в эконометрике появилось разнообразие критериев сравнения. Стало возможным получение эконометрических законов и прогнозов прямо на фазовых портретах и параметрических картинах. Сплайн-подход выявил новые для эконометрики аналитические представления дискретных регрессионных соотношений.

Особенностью предлагаемого метода является конструктивность с доведением теории до реальных характеристик, с выделением важных и легко оцениваемых показателей, что позволяет просто, быстро и точно получать решение, в чём-то лучшее остальных, не требуя разных соображений, представлений, преобразований, допущений.

Малая степень составляющих сплайна и малый порядок его производных облегчают экономическую интерпретацию модели, это хорошо соотносится с тем, как экономист понимает, объясняет и управляет экономическим поведением, позволяет менеджерам легче расшифровывать экономический смысл сплайн-образов показателей. Теперь экономисты могут привлечь для исследования динамики экономических показателей всю гамму методов аналитического математического аппарата, найти крутизну участков подъёма и спада, точки экстремумов, построить фазовые портреты и параметрические картины взаимозависимостей с непрерывными кривыми, генерировать и визуализировать новые законы, находить прогнозы. Простота получения сплайнов любых степеней, надёжность работы алгоритма сплайн-аппроксимации, широкие возможности и наглядность сплайн-визуа- лизации дают в руки менеджера понятное, практическое орудие моделирования, мониторинга, анализа и прогнозирования рынка.

Требуется, чтобы система функций была исследована и достаточно широко применена математиками, тогда при преобразованиях гарантируется правильность и надёжность результатов. Это положение верно, математические сплайны известны с 1949 г. (Шёнберг) и с тех пор широко используются в научных и технических приложениях.

Так как сплайн проходит точно через все узлы «решётчатой» функции, то сплайн-моделирование, сплайн-прогнозирование, сплайн-анализ точны по сути, они лучше и тоньше определяют и сохраняют спектральный состав процесса, значительно улучшают интерполяцию, надёжнее накапливают статистику процесса в отчётном периоде.

Всё это приводит к констатации итогового факта, что сплайн-аппроксимационный подход, заменяющий «решётчатые» функции экономических процессов гладкими аналитическими функциями невысокой степени (1..4) и несколькими их непрерывными же производными с малыми степенями (0..3), важен для экономической динамики.

В третьем разделе ««Циклическая» парадигма исследования» представлены способы использования сплайнового представления для перехода от временных рядов экономических показателей рынка к фазовым соотношениям. При этом аналитические возможности экономического сплайн-анализа усложняются и расширяются, что демонстрируется и визуализируется динамикой экономического поведения на фазовых сплайн-портретах в двух и трёх измерениях. Методами фазового анализа в параметрической форме (параметр - время) удаётся изучать взаимную зависимость переменных в многозначных функциях, характерных для регрессионных соотношений в эконометрике.

Фазовые портреты играют важную роль в математике и технике. Фазовым портретом называется построенная на плоскости кривая, представляющая собой зависимость первой производной Y’(t) от самой переменной Y(t), время t играет роль параметра. Отрезок прямой на фазовом портрете, находящийся над осью абсцисс и параллельный ей, на привычном дискретном «решётчатом» графике {át_j,Y_jñ} соответствует линейному росту переменной Y(t), так как первая производная положительна и постоянна, а переменная Y(t) растёт вдоль оси абсцисс слева направо. Замкнутый цикл фазового портрета указывает на стабильные периодические колебания переменной Y(t), «раскручивающаяся» спираль свидетельствует о росте амплитуды колебаний со временем, «сворачивающаяся» спираль соответствует затуханию периодической составляющей. Фазовый портрет может быть и пространственным (трёхмерным), тогда его координатными осями являются: сама функция; её первая производная; независимая переменная, в качестве которой оказывается удобным брать текущее время.

Следующим полезным инструментом сплайн-анализа является получение взаимных зависимостей характеристик рынка на параметрических сплайн-картинах зависимостей одних экономических показателей от других. Непрерывность сплайн-образов облегчает понимание инерционности, взаимной увязки разных процессов рынка. Переход от временных рядов экономических показателей к параметрическим картинам взаимозависимостей позволяет перейти к новому демонстрационному качеству при построении параметрических кривых в двух и трёх измерениях, когда в одной координатной системе можно увидеть взаимодействие экономических переменных друг с другом.

Фазовый сплайн-анализ в наших исследованиях и вычислительных экспериментах показал, что широкий спектр экономических, маркетинговых и финансовых показателей имеет принципиально циклическую природу. Повсюду в экономике мы видим богатство циклических конструкций, которые необходимо обнаруживать, исследовать, объяснять, обсчитывая показатели циклов. Выявленная цикличность позволяет по-новому взглянуть на многие экономические процессы, поэтому можно с полным правом выделить новый раздел экономики - «экономическую цикломатику». Складывается впечатление, что в экономике тренды как таковые просто не существуют, они строятся интерполяционно через характерные точки циклов (центры, точки пересечения ветвей и пр.).

В четвёртом разделе «Циклы в макроэкономике» описаны особенности периодических движений макроэкономических показателей. Именно в макроэкономике ярко проявляется цикличность, здесь происходит круговорот таких глобальных категорий, как ВВП, инфляция, безработица, норма процента, валютные курсы, цены на нефть. Было принято считать, что мегаэкономическое поведение в долгосрочном периоде трендово, а экономические флуктуации характерны для краткосрочной динамики. Это утверждение основывалось на том, что тренд интегрирует случайные выбросы и в итоге представляет собой устойчивую тенденцию, гладкую кривую с минимумом экстремумов, проходящую через характерные точки показателя.

Колебания большинства макроэкономических показателей синхронизованы (рис. 6) и ведущую роль играет обобщающий показатель экономической деятельности – реальный объём ВВП. Когда во время рецессии реальный объём ВВП снижается, то же происходит и с личными доходами, прибылью корпораций, потребительскими расходами, инвестициями, объёмом промышленного производства, объёмом розничных продаж и т.д., ибо спад отражается во всей экономике и проявляется почти во всех макроэкономических показателях. Хотя большинство макроэкономических переменных изменяется синхронно, можно, забегая вперёд, сказать – синфазно, временные лаги, формы, амплитуды и периоды их колебаний могут быть весьма различны.

Согласно теориям делового цикла, движущими силами экономических периодических движений выступают:

• по Дж.М. Кейнсу - колебания совокупного спроса, при этом совокупный спрос определяет объём инвестиций, колебания которого, в свою очередь, вызывают колебания уровня деловой активности;
  
• по К. Марксу - колебания нормы прибыли;
  
• по М. Фридману - колебания предложения денег;
  
• по Й. Шумпетеру - технологические изменения (инновации).
  

Модель совокупного спроса и совокупного предложения ложится рабочим инструментом в основу классической «теории экономических флуктуаций». Взаимодействие уровня цен и объёма выпускаемой продукции в конечном итоге приводит к установлению равновесия совокупного спроса и совокупного предложения. Взаимные перемещения показателей с временными задержками от точки к точке на кривых совокупного предложения и совокупного спроса приводят к колебаниям параметров в системе. И в этом случае работает гипотеза, объясняющая колебания наличием в замкнутой экономической системе «чистого» запаздывания, так как предложение обязательно следует за спросом с некоторым временным лагом.

Как мы увидим, инфляция в высшей мере циклична, в связи с этим круговорот её значений может оказаться весьма полезным как в экономическом анализе, так и при прогнозировании. Начнём изучение цикличности макроэкономического показателя «инфляция» предлагаемыми методами с американской экономики, поскольку её динамика хорошо известна и точна, на рис. 6 показан её фазовый сплайн-образ. Аналогично построены фазовые портреты ВВП, уровня безработицы, мировых цен на нефть, заработной платы, индекса потребительских цен и пр. как для экономики США, так и России. На параметрических картинах взаимосвязей этих показателей можно увидеть и «инфляционную спираль» заработной платы и цен, которая на деле оказалась вовсе не спиралью, и кривую Филлипса - как частный случай взаимосвязи уровня безработицы и темпа инфляции и пр.

В пятом разделе «Циклы в региональном продовольственном маркетинге» оказалось необходимым начать с проблемы сбора сведений о нём самом. Задачи «тонкого» анализа региональной экономической ситуации требуют новых адекватных методов мониторинга деятельности субъектов на рынке. Сведения о региональном продовольственном рынке невозможно получить привычным изъятием данных из официальных статистических отчётов, федеральных или региональных. Количество видов продуктов, продаваемых одной фирмой, превышает многие сотни, динамика каждого продукта своеобразна по своим ценовым характеристикам, времени хранения, по потреблению населением в разные периоды и т.д. Сведения о доходности, динамике объёмов продаж, по видам продуктов, по отдельным предпринимателям отсутствуют и относятся к коммерческой тайне.

Поэтому в исследовании пришлось обратиться к разработке специфических способов мониторинга и анализа регионального продовольственного рынка, включая и поиск его цикломатичности. Для этих целей в ОАО «КавМком» - торговом представительстве холдинга ЗАО «Микояновский мясокомбинат» по Югу России - была разработана и в настоящем исследовании использована интегрированная компьютерная система учёта, анализа и прогнозирования финансово-хозяй- ственной деятельности предприятия оптовой торговли – ИКС УАП ФХД ПОТ, совмещающая в себе данные для ведения корпоративного бухгалтерского, налогового и оперативного управленческого учёта, позволяющая формировать отчёты электронного формата с возможностью выгрузки данных из программы «1С: Предприятие» и транспортировки данных в центральный офис по электронной почте.

Это пришлось сделать, так как существующие бухгалтерские системы по своему содержанию и назначению не позволяют в полной мере решать задачи вычисления ёмкости рынка, управления региональным бизнесом и оперативного контроля деятельности торговых представительств. Система принципиально отличается от известных систем в первую очередь повсеместным использованием первичных показателей. Раз важная роль отводится адекватности и точности исходных данных, то показатели для финансовых, налоговых, бухгалтерских отчётов берутся из списка первичных, чтобы при ошибках вычисления вторичных показателей допущенные погрешности не «расползались» бы по документам (отчётам), генерируемым системой.

Вторая особенность построенной системы используется в данном исследовании – все взаимосвязи показателей графически изображаются прямо на поле документа стрелками. Они показывают способ комплектования каждого показателя из первичных, что позволяет не только проверять механизм генерации вторичных показателей, лучше понимать механику их текущего изменения, но и помогает правильно составлять эконометрические законы и балансы регионального маркетинга для последующего анализа, поиска циклов и прогнозирования.

Третья особенность – охват всех отчётных, налоговых, бухгалтерских, финансовых документов одной системой. Итогом работы первого блока системы является электронный файл в формате EXCEL, включающий в себя девять отчётных документов, формирующих базу данных обо всех аспектах финансово-хозяйственной деятельности торгового представительства. Каждый отчёт представлен электронными таблицами, данные в них увязаны математическими зависимостями не только с соответствующими данными самого отчёта, но (в большей или меньшей степени) и с показателями других отчётов. Всё это обеспечило исследование хорошо проверенными, точными и надёжными данными, гарантирующими как качество, так и валидацию последующего мониторинга, анализа и строящегося прогноза.

С помощью сплайн-подхода обнаружена стабильная периодичность в объёмах и доходности реализации практически всего спектра колбасной продукции в регионе, обнаруженные перманентные циклы динамики рыночных показателей оказываются не случайными. На рис. 7 показан фазовый портрет динамики городской торговли варёными колбасами, её «систематическая цикломатика». Последующее прогнозирование может использовать циклические построения.

Рисунок 7 - Фазовый портрет городской (City) торговли (RED), систематическая цикломатика. Кубические сплайн-образы. По оси абсцисс - объём продаж варёных колбас в виде SPL3_WeightCity, по оси ординат - первая производная SPL3_WeightCity1D. Временной интервал - от сентября 2003 (03/09) до сентября 2004 (04/09) гг. Почти идеальные четырёхмесячные циклы. Объём торговли в сентябре не изменяется год от года, но 2003 г. отмечен более высокой тенденцией. Максимальный объём продаж – в конце апреля 2004 г., минимальный – ближе к концу ноября 2003 г. Менеджмент среднего качества