Вавилова закон

Вид материала

Закон

Содержание Временное сопротивление Время-пролётный масс-спект­рометр Всемирного тяготения закон Крупнейшие установки со встречными пучками и их параметры Рис. 1. Схема установки со встречными электрон-позитронными пучками. Пучок уско­ренных в синхротроне С электронов (е Вторичная электронная эмис­сия Рис. 2. Зависимость коэфф.  и  от энергии первичных эл-нов: вверху — для металлов; внизу — для диэлектриков и ПП. Вторичное квантование Второе начало термодинами­ки Q — переданное системе кол-во теплоты, А — Статистическая физика

Подобный материал:

• Н. И. Вавилова аналитический отчет, 217.51kb.
• Урок по общей биологии в 11 классе «Дело академика Вавилова», 851.64kb.
• Селекция- одомашнивание, 126.51kb.
• Уважаемые коллеги!, 64.43kb.
• Українське товариство генетиків І селекціонерів ім. М.І. Вавилова, 45.97kb.
• «Саратовский государственный аграрный университет имени Н. И. Вавилова», 377.27kb.
• Саратовский Государственный Аграрный Университет им. Н. И. Вавилова. Кафедра Акушерства, 248.61kb.
• О. Б. Ширяев Институт общей физики ран, 119991, Москва, ул. Вавилова,, 20.28kb.
• Главное управление образования, 70.84kb.
• Издательский дом, 529.99kb.

ВРЕМЕННОЕ СОПРОТИВЛЕНИЕ, см. Прочности предел.

ВРЕМЯ, см. Пространство и время.

ВРЕМЯ ЖИЗНИ, 1) средняя продол­жительность  существования возбуж­дённых состояний молекул, атомов,

ядер атомных, заканчивающаяся спон­танным (самопроизвольным) их пере­ходом в менее возбуждённое или в осн. состояние; т — важная хар-ка состояний или уровней энергии ч-ц (В. ж. на уровне).

2) Ср. продолжительность жизни нестабильных (радиоактивных) ат. ядер и элем. ч-ц, связанная с их пери­одом полураспада T_1/2 и с постоянной распада , соотношением:

 = T_1/2/ln2=1/

(т изменяется в широких пределах, напр. для ²³⁸U =4,49•10⁹ лет, для свободного нейтрона 12,8 мин, для ²¹²Ро 3•10^-7 с, для °-мезона 10^-16 с).

3) Ср. продолжительность жизни квазичастиц в тв. теле и в жидком ге­лии, в частности неравновесных эл-нов проводимости и дырок в полупровод­никах, определяемая процессами ре­комбинации электронов и дырок. Она зависит от природы кристалла, от темп-ры, хар-ра и концентрации при­месей и колеблется в пределах 10^-2— 10^-8 с.

ВРЕМЯ-ПРОЛЁТНЫЙ МАСС-СПЕКТ­РОМЕТР, динамич. масс-спектро­метр, в к-ром для разделения ионов по величине отношения массы к за­ряду используется различие во вре­мени пролёта ионами определ. рас­стояния. Отличаются быстродействи­ем — скорость измерений до 10⁵ масс-спектров в 1 с; широко используются при изучении быстропротекающих про­цессов.

ВСЕМИРНОГО ТЯГОТЕНИЯ ЗАКОН (Ньютона закон тяготения), см. в ст. Тяготение.

ВСТРЕЧНЫХ ПУЧКОВ СИСТЕМЫ, установки, в к-рых осуществляется столкновение встречных пучков заряж. ч-ц (элем. ч-ц и ионов), ускорен­ных электрич. полем до высоких энер­гий (см. Ускорители). В таких уста­новках исследуются вз-ствия ч-ц и рождение новых ч-ц при максимально доступных в лаб. условиях эфф. энер­гиях столкновения. Наибольшее рас­пространение получили устройства со встречными электрон-электронны­ми (е^-е^-), электрон-позитронными (е^-е⁺) и протон-протонными (рр) пуч­ками.

В обычных ускорителях вз-ствие ч-ц изучается при столкновениях пуч­ка ускоренных до высокой энергии ч-ц с ч-цами неподвижной мишени. При этом вследствие закона сохранения полного импульса соударяющпхся ч-ц б. ч. энергии налетающей ч-цы расхо­дуется на сообщение кинетич. энергии ч-цам — продуктам реакции, и лишь небольшая её часть «включается» в энергию вз-ствия ч-ц в системе их центра инерции, к-рая может идти, напр., на рождение новых ч-ц. При столкновении двух ч-ц одинаковой массы m₀, одна из к-рых покоится в лаб. системе отсчёта, а другая движет­ся с релятивистской (близкой к скоро­сти света с) скоростью, энергия в системе центра инерции ξ_ци=2ξ₀ξ, где ξ₀=m₀c² — энергия покоя ч-цы, а £ — энергия налетающей ч-цы в лаб. системе отсчёта. Чем больше ξ, тем меньшая её доля определяет энер­гию вз-ствия ч-ц. Если же сталкива­ются ч-цы с равными по величине и противоположно направленными им­пульсами, т. е. их суммарный импульс равен 0, то лаб. система отсчёта совпа­дает с системой центра инерции ч-ц н эфф. энергия столкновения равна сум­ме энергий сталкивающихся ч-ц; для ч-ц с одинаковыми массами (и энергией

ξ₁) ξ_ци=2ξ₁.

Особенно велико преимущество изу­чения процессов вз-ствия на встречных пучках для лёгких ч-ц — эл-нов и по­зитронов, для к-рых ξ₀=0,5 МэВ. Напр., для соударяющихся во встреч­ных пучках эл-нов с энергией 1 ГэВ ξ_ци=2 ГэВ; такая же эфф. энергия столкновения при одном неподвижном эл-не потребовала бы энергии налетаю­щего эл-на ξ=ξ²_ци/2ξ₀4000 ГэВ. Для встречных пучков протонов (ξ₀1 ГэВ), напр, с энергией ξ=70 ГэВ (энергия протонов Серпуховского ус­корителя 76 ГэВ), ξ_ци=140 ГэВ, тогда как при столкновении с поко­ящимся протоном эфф. энергия столк­новения 140 ГэВ была бы достигнута лишь при энергии налетающего про­тона в лаб. системе ξ=10000 ГэВ. Т. о., в области сверхвысоких энергий с В. п. с. не могут конкурировать обыч­ные ускорители с неподвижной ми­шенью.

Недостаток В. п. с.— малая интен­сивность пучков (число ч-ц в пучках) по сравнению с плотностью ч-ц в не­подвижной мишени. Для увеличения интенсивности до процесса соударения производится накапливание заряж. ч-ц в спец. накопит. кольцах, так что­бы токи циркулирующих ч-ц были не менее десятков А. Однако и при таких токах интенсивность пучков вторич­ных ч-ц высоких энергий (^- и К-мезонов, нейтрино и др.), образующихся при соударениях, на неск. порядков меньше, чем интенсивность пучков тех же ч-ц от обычных ускорителей. Кроме того, в В. п. с., по сравнению с традиц. ускорителями, получается про­игрыш в энергии вторичных ч-ц, т. к. энергия вторичной ч-цы не может превышать энергию сталкивающихся первичных ч-ц. Поэтому В. п. с. не могут заменить традиц. ускорители, а лишь дополняют их.

В накопит. кольца — кольцевые ва­куумные камеры, помещённые в магн. поле, ускоренные заряж. ч-цы посту­пают из обычного ускорителя. Магн. поле создаётся, как правило, секторными магнитами, разделёнными пря­молинейными промежутками (без магн.. поля) для областей пересечения пучков (и для размещения ускорит. устройства). В. п. с. содержит один или два накопит. кольца в зависимо­сти от того, различны (напр., е^-е⁺, рр, где р — антипротон) или одинаковы

92


(напр., е^-е^-, рр) знаки электрич. заря­дов сталкивающихся ч-ц. Предварит. ускорение пучков (до инжекции в накопит. кольца) производится в син­хротронах или синхрофазотронах, а также в линейных ускорителях. Воз­можно и дополнит. ускорение ч-ц в накопит. кольцах после инжекции. Однако независимо от того, произво­дится ли дополнит. ускорение, каждый накопит. комплекс со встречными пуч­ками обязательно включает ускоряю­щую систему для компенсации потерь энергии заряж. ч-ц на синхротронное излучение (для пучков е^-е^- и е^-е⁺ ) и ионизацию остаточного газа в каме­ре. Второе назначение системы уско­рения — фиксация азимутальных раз­меров пучка (число сгустков ч-ц равно кратности частоты ускоряющей систе­мы по отношению к частоте обраще­ния ч-ц). Типичные схемы электрон-позитронного и протон-протонного накопит. комплекса приведены на рис. 1 и 2.

Осн. хар-ка системы со встречными пучками — величина, к-рая определяет число событий (N) исследуемого типа в ед. времени; она наз. свети­мостью установки (L).

КРУПНЕЙШИЕ УСТАНОВКИ СО ВСТРЕЧНЫМИ ПУЧКАМИ И ИХ ПАРАМЕТРЫ





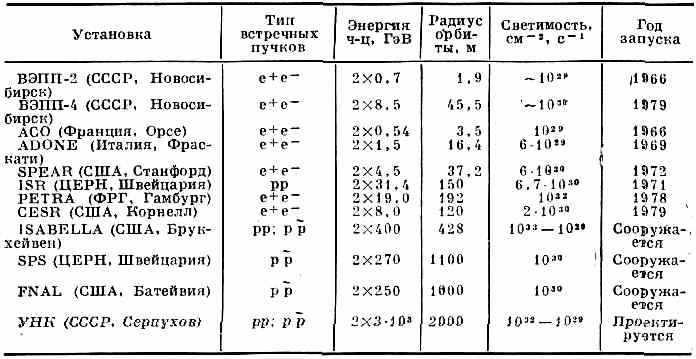
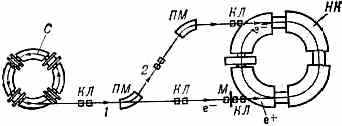
Рис. 1. Схема установки со встречными электрон-позитронными пучками. Пучок уско­ренных в синхротроне С электронов (е^-) выводится по каналу 1 и попадает на ми­шень М, в к-рой рождаются позитроны (е⁺). В течение нек-рого времени позитроны на­капливаются в накопит. кольце НК, после чего включаются поворотные магниты ПМ, с помощью к-рых электронный пучок из С направляется по каналу 2 в НК навстречу позитронам, и происходит столкновение пуч­ков е⁺е^- (КЛ — фокусирующие магн. квадрупольные линзы).



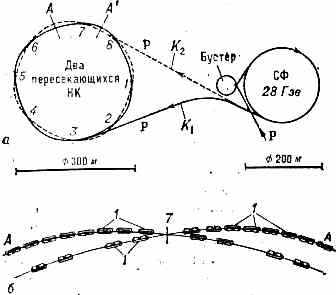
Рис. 2. а — схема расположения синхрофа­зотрона (СФ) и двух пересекающихся на­копит. колец НК, в к-рых происходят про­тон-протонные столкновения (ЦЕРН): 1—8— места пересечения колец; стрелки указывают направление движения протонов; K₁ К₂ — каналы для ввода протонов .в НК (в бустере производится предварит. ускорение прото­нов; в НК протоны дополнительно ускоря­ются до 31,4 ГэВ); б — деталь пересечения пучков протонов между сечениями АА' (1 — элементы структуры магнита, фокусирую­щего пучки протонов).


Если изу­чается вз-ствие с сечением а, то N=L. В наиболее простом случае, ког­да угол встречи пучков равен нулю, L=R(N₁N₂/S)/2, где N₁,N₂— полные числа ч-ц в каждом пучке, заполняющем кольца, S — площадь поперечного сечения, общая для обоих пучков,  — круговая частота обра­щения ч-ц по замкнутой орбите, R — коэфф. использования установки, рав­ный отношению длины промежутков встречи пучков к периметру орбиты. В более общем случае R зависит от области перекрытия пучков, т. е. от углов пересечения и относит. размеров пучков. Для эфф. изучения, процессов вз-ствия с сечением =10^-26—10^-32 см² величина светимости должна состав­лять 10²⁸—10³² см^-2 с^-1. Это дости­гается накоплением циркулирующего тока пучков заряж. ч-ц и уменьшением поперечного сечения пучков при помо­щи спец. магн. фокусировки в прямо­линейных промежутках, а также ис­пользованием методов электронного (стохастического) охлаждения с целью уменьшения поперечной компоненты импульса сталкивающихся пучков. Ме­тод электронного охлаждения был предложен в 1966 Г. И. Будкером для тяжёлых ч-ц (протонов и антипротонов), у к-рых из-за практич. отсутст­вия еинхротронного излучениями не про­исходит автоматич. затухания поперечных колебаний ч-ц в пучке. Метод основан на эффекте передачи тепловой энергии пучка тяжёлых ч-ц сопутству­ющему (пущенному . параллельно) электронному пучку с более низкой темп-рой. Эксперим. подтверждение этого эффекта было впервые получено в Институте ядерной физики Сибирско­го отделения АН СССР (1974).

• Для того чтобы обеспечить непре­рывный физ. эксперимент с мало ме­няющейся светимостью установки, не­обходимо большое время жизни на­копленных пучков ч-ц. Время жизни пучка (время, в течение к-рого интен­сивность пучка уменьшается в е раз)

зависит от ряда эффектов. Гл. из них— однократное и многократное рассея­ние ускоренных ч-ц на атомах остаточ­ного газа в камере накопителя, а для эл-нов и позитронов — синхротронное излучение и квант. флуктуации; суще­ственную роль может также играть эф­фект взаимного рассеяния эл-нов (по­зитронов) пучка. Эксперим. критерий времени жизни пучка — относит. ве­личина потери интенсивности пучков в % за 1 ч; для лучших действующих установок она составляет десятые доли % в час (для протонной установки в ЦЕРНе — 0,1% в 1 ч при токе 22 А). Такая большая величина времени жиз­ни пучков достигается при помощи сверхвысокого вакуума в камерах на­копителей пучков (10^-11 мм рт. ст. в камере и 10^-12 мм рт. ст. в зонах встречи пучков). Необходимый эле­мент ускорителя со встречными е^-е⁺-пучками — электрон-позитронный кон­вертор (металлич. мишень М толщиной ок. 1 радиац. длины; на рис. 1 — на прямом пучке), в к-рой эл-ны рож­дают тормозные -кванты, а те в свою очередь — пары электрон — позитрон. Отношение числа позитронов, захва­ченных в накопитель, к числу эл-нов, выведенных из синхротрона (коэфф: конверсии), при энергии электронного пучка в сотни МэВ может достигать величины 10^-4 для позитронного пучка с энергией, примерно вдвое меньшей энергии эл-нов.

Для схемы протон-протонных столк­новений (рис. 2), реализуемой на базе двух магн. структур с сильной фокуси­ровкой, характерно наличие многих точек встречи пучков, что позволяет одновременно проводить неск. физ. экспериментов.

Типичные параметры наиб. крупных В. п. с. приведены в таблице. :.Историческая справка. Разработка и сооружение .эксперим. установок для исследований на встреч­ных пучках ч-ц были начаты в 1956 в СССР и за рубежом по предложению

93


амер. физика Д. У. Керста. В течение 1956—66 преимущество в реализации встречных пучков было отдано лёгким стабильным ч-цам — эл-нам и позитро­нам (предложение о реализации уско­рителей со встречными электрон-позитронными пучками принадлежит Г. И. Будкеру), для к-рых ультрарелятив. скорости достигаются при энергиях в сотни МэВ. В связи с запуском в 1959— 1960 высокоэнергичных ускорителей протонов в ЦЕРНе на 28 ГэВ и в США на 33 ГэВ открылись возможности для создания накопит. колец на встречных рр-пучках. В 1971 в ЦЕРНе были за­пущены два накопит. кольца для встречных рр-пучков с энергией 31,4 Гэв. Успешная эксплуатация этой установки при циркулирующих токах протонов 22—25 А стимулировала дальнейшее развитие проектных работ по рр-, рр:- и ре^--накопительным уста­новкам высоких энергий.

• Будкер Г. И., Ускорители и встреч­ные пучки, в кн.: Труды VII Международ­ной конференции по ускорителям заряженных частиц высоких энергий, т. 1, Ер., 1970, с. 33; Встречные пучки. Шестое Всесоюзное совещание по ускорителям заряженных час­тиц (Дубна, 1978), Дубна, 1978, с. 13; X Меж­дународная конференция по ускорителям заряженных частиц высоких энергий (Протвино, 1977), т. 1, Серпухов, 1977, с. 17—29, 30—40.

В. П. Дмитриевский.

ВТОРИЧНАЯ ЭЛЕКТРОННАЯ ЭМИС­СИЯ, испускание эл-нов (вторичных) тв. и жидкими телами (эмиттерами) при их бомбардировке эл-нами (пер­вичными). При толщине эмиттера, меньшей пробега первичных эл-нов, вторичные эл-ны эмиттнруются как со стороны бомбардируемой поверхности (В. э. э. «на отражение»), так ц с её обратной стороны (В. э. э. «на про­стрел»). Вторичные эл-ны имеют не­прерывный энергетич. спектр от 0 до энергии ξ_п первичных эл-нов (рис. 1). Они состоят из упруго (ξ=ξ_п) и неупруго (условно ξ50 эВ) отра­жённых первичных и истинно вторич­ных эл-нов (ξ50 эВ) — эл-нов в-ва, получивших от первичных эл-нов энер­гию, достаточную для выхода в ваку­ум. Их наиболее вероятная энергия — 2—4 эВ для металлов и порядка 1 эВ для диэлектриков. Тонкая структура энергетич. спектра эл-нов обусловлена характеристич. потерями эл-нов на возбуждение атомов в-ва (см. Характе­ристические спектры) и Оже эффектом и позволяет судить о хим. составе и электронном состоянии атомов поверх­ностного слоя тв. тела.

Количественно В. э. э. характеризу­ется коэффициентом В. э. э. о, равным:



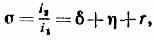
где i₁ — ток, создаваемый первичными эл-нами, i₂ — всеми вторичными,  — ноэфф. истинной В. э. э.,  и r — коэфф. неупругого и упругого отражения эл-нов. Если ξ_п<100эВ, то =+r,



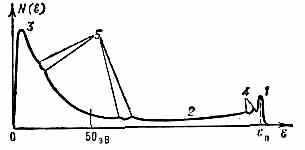
Рис. 1. Распределение вторичных эл-нов по энергиям: 1 — упруго отражённые эл-ны; 2 — неупруго отражённые эл-ны; 3 — ис­тинно вторичные эл-ны; 4 — пики характе­ристич. потерь; 5 — Оже-электроны; ξ_п — энергия первичных эл-нов.


а при ξ_п>100—200 эВ =+). Коэфф. , , , r зависят не только от энергии, но и от угла падения первич­ных эл-нов, природы и структуры в-ва, состояния поверхности, темп-ры. Для монокристаллов эти зависимости об­ладают тонкой структурой, обуслов­ленной дифракцией электронов (см. Дифракция микрочастиц), когерентно рассеянных разл. плоскостями кри­сталла.

Истинно вторичные эл-ны эмиттируются из приповерхностного слоя толщиной Я. В металлах, где в резуль­тате вз-ствия с эл-нами проводимости



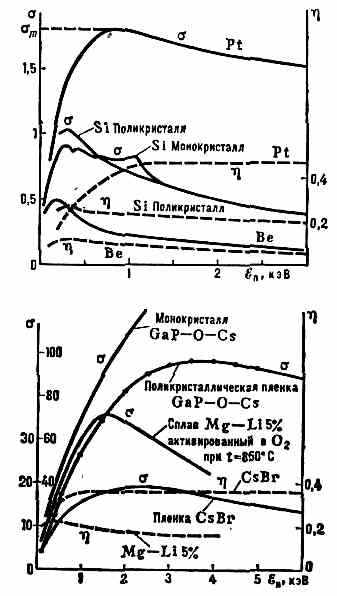
Рис. 2. Зависимость коэфф.  и  от энергии первичных эл-нов: вверху — для металлов; внизу — для диэлектриков и ПП.


первичные эл-ны быстро теряют энер­гию,  и  малы (~30 Å, ~0,4—1,8, рис. 2). В диэлектриках с широкой запрещённой зоной и малым сродством к электрону  эл-ны, возбуждённые в зону проводимости, могут терять энер­гию в осн. лишь на возбуждение

колебаний кристаллической решётки. Эти потери невелики, поэтому диэлект­рики обладают большими значениями (300—1200 Å) и (20—40) при ξ_п порядка неск. сотен В. Из диэлектрич. слоев изготавливают эфф. эмиттеры вторичных эл-нов. В ПП эмиттерах вторичных эл-нов с отрицат. электрон­ным сродством (<0) даже те эл-ны, к-рые движутся к поверхности с очень малыми энергиями (~kT), также мо­гут выйти в вакуум. Поэтому такие эмиттеры обладают ещё большими зна­чениями  и  (рис. 2). Создание в диэлектрике, особенно в пористых слоях, сильного электрич. поля (10⁵— 10⁶ В/см) приводит к росту  до 50— 100 (В. э. э., усиленная полем).

• Бронштейн И. М., Фрайман Б. С., Вторичная электронная эмиссия, М., 1969; Шульман А. Р., Фридрихов С. А., Вторично-эмиссионные мето­ды исследования твердого тела, М., 1977; Добрецов Л. Н., Гомоюнова М. В., Эмиссионная электроника, М., 1966.

И. М. Бронштейн.

ВТОРИЧНОЕ КВАНТОВАНИЕ, ме­тод описания квант. систем, состоящих из большого числа тождеств. ч-ц, в к-ром роль независимых переменных волн. ф-ции играют числа заполнения — числа ч-ц в индивидуальных состоя­ниях отд. ч-цы. Развит в 1927 англ. физиком П. Дираком для бозонов и в 1928 распространён амер. физиком Ю. П. Вигнером и нем. физиком П. Иорданом на фермионы. В. к. осуще­ствляется введением операторов, уве­личивающих и уменьшающих число ч-ц в данном состоянии на единицу (они наз. операторами рождения и уничтожения ч-цы). Матем. св-ва этих операторов задаются перестановочны­ми соотношениями, вид к-рых опреде­ляется спином ч-ц, т. е. типом квант. статистики, к-рой подчиняются ч-цы. При таком описании волн. ф-ция сама становится оператором.

Метод В. к. необходим в релятив. теории (в квант. теории поля), описы­вающей системы с изменяющимся чис­лом ч-ц. Ф-ции поля (напр., электро­магнитного) рассматриваются как опе­раторы, действие к-рых отражает рож­дение и поглощение квантов поля; вид перестановочных соотношений для опе­раторов зависит от спина этих квантов. Подробнее см. Квантовал теория поля.

А. В. Ефремов.

ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИ­КИ, один из осн. законов термоди­намики; устанавливает необратимость макроскопич. процессов, протекающих с конечной скоростью: процессы, свя­занные с теплообменом при конечной разности темп-р, с трением, с диффу­зией, с выделением джоулевой теплоты и др., текущими с конечной скоростью, необратимы, т. е. могут само­произвольно протекать только в одном направлении.

Исторически В. н. т. возникло из анализа работы тепловых машин (франц. учёный С. Карно, 1824). Су­ществует неск. эквивалентных форму­лировок В. н. т. Само название «В. н. т.» и исторически первая его формули-

94


ровка (1850) принадлежат нем. учёно­му Р. Клаузиусу: невозможен про­цесс, при к-ром теплота переходила бы самопроизвольно от холодных тел к телам нагретым. При этом самопроиз­вольный переход не следует понимать в узком смысле: невозможен не только непосредств. переход, его невозможно осуществить и при помощи машин или приборов без того, чтобы в природе не произошли ещё к.-л. изменения (механич., тепловые и т. д.). Иными слова­ми, невозможно провести процесс, единственным следствием к-рого был бы переход теплоты от хо­лодного тела к нагретому. Если бы (в нарушение положения Клаузиуса) та­кой процесс оказался реально осущест­вимым, то можно было бы, разделив один тепловой резервуар на две части и переводя теплоту из одной части в другую, получить два резервуара с разл. темп-рами. Это позволило бы многократно осуществить с этими ре­зервуарами Карно цикл и получить механич. работу при помощи периоди­чески действующей (т.е. в конце каж­дого цикла возвращающейся к исход­ному состоянию) машины за счёт внутренней энергии одного теплового резервуара. Поскольку это невозмож­но, в природе невозможны процессы, единств. следствием к-рых было бы совершение механич. работы, произве­дённой в результате охлаждения теп­лового резервуара (формулировка англ. физика У. Томсона, 1851). Об­ратно, если бы можно было получить механич. работу за счёт внутр. энер­гии одного теплового резервуара (в противоречии с В. н. т., по Томсону), то можно было бы нарушить и поло­жение Клаузиуса. Механич. работу, полученную за счёт теплоты от более холодного резервуара, можно было бы использовать для нагревания более тёплого резервуара (напр., трением) и тем самым осуществить переход теп­лоты от холодного тела к нагретому без изменения состояния к.-л. иных тел.

В реальных тепловых двигателях процесс превращения теплоты в рабо­ту обязательно сопряжён с передачей определ. кол-ва теплоты внеш. среде. В результате тепловой резервуар дви­гателя охлаждается, а более холодная внеш. среда нагревается, что находит­ся в согласии с В. н. т. Нарушение В. н. т. означало бы возможность соз­дания т. н. вечного двигателя 2-го рода, совершающего работу за счёт внутр. энергии теплового резервуара и не из­меняющего термодинамич. состояния окружающих тел. Следовательно, В. н. т. можно формулировать и как невозможность создания веч­ного двигателя 2-го рода (нем. физик В. Оствальд, 1888). -Г. А. Зисман. В совр. термодинамике В. н. т. фор­мулируется как закон возрастания энтропии S. Согласно этому закону, в замкнутой макроскопич. системе эн­тропия при любом реальном процессе либо возрастает, либо остаётся неизменной, т. е. изменение энтропии S0 (равенство имеет место для об­ратимых процессов). В состоянии рав­новесия энтропия замкнутой системы достигает максимума и никакие макро­скопич. процессы в такой системе, со­гласно В. н. т., невозможны. Приве­дённые в начале статьи формулировки В. н. т. представляют собой частные выражения общего закона возрастания энтропии.

Для незамкнутой системы направ­ление возможных процессов, а также условия равновесия могут быть выве­дены из закона возрастания энтропии, применённого к составной замкнутой системе, получаемой путём присоеди­нения всех тел, участвующих в про­цессе. Это приводит в общем случае необратимых процессов к неравенствам:



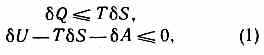
где  Q — переданное системе кол-во теплоты, А — совершённая над ней работа, U — изменение её внутр. энергии; знак равенства относится к обратимым процессам.

Важные следствия даёт применение В. н. т. к системам, находящимся в фиксированных внеш. условиях. Напр., для систем с фиксированной темп-рой и объёмом неравенство (1) приобретает вид: F0, где F=U-TS— свободная энергия системы (Гельмгольца анергия). Т. о., в этих условиях направление реальных процессов оп­ределяется убыванием F, а состояние равновесия — минимумом этой вели­чины (см. Потенциалы термодинами­ческие).

В. н. т., несмотря на свою общность, не имеет абс. хар-ра, и отклонения от него (флуктуации) явл. вполне зако­номерными. Примерами флуктуац. процессов могут служить: броуновское движение ч-ц, равновесное тепловое излучение нагретых тел (в т.ч. радио­шумы), возникновение зародышей но­вой фазы при фазовых превращени­ях, самопроизвольные флуктуации темп-ры и давления в равновесной системе и т. д.

Статистическая физика, построен­ная на анализе микроскопич. меха­низма явлений, происходящих в мак­роскопич. телах, и выяснившая физ. сущность энтропии, позволила понять природу В. н. т., определить пределы его применимости и устранить кажу­щееся противоречие между механич. обратимостью любого, сколь угодно сложного, микроскопич. процесса и термодинамич. необратимостью про­цессов в макротелах. Как показывает статистич. термодинамика (австр. фи­зик Л. Больцман, амер. физик Дж. У. Гиббс), энтропия системы связана со статистическим весом Р макроско­пич. состояния: S=klnP. Статистич. вес Р пропорц. числу разл. микроско­пич. реализаций данного состояния макроскопич. системы (напр., разл. распределений значений координат и

импульсов молекул газа, отвечающих определ. значениям энергии, давления и др. термодинамич. параметров газа). Для замкнутой системы вероятность термодинамическая W данного макро­состояния пропорц. его статистич. весу и определяется энтропией системы:

W ~ exp (S/k), или S~klnW. (2)

Т. о., закон возрастания энтропии имеет статистически-вероятностный хар-р и выражает пост. тенденцию сис­темы к переходу в более вероятное со­стояние. Максимально вероятным явл. состояние равновесия; за достаточно большой промежуток времени любая замкнутая система достигает этого со­стояния.

Энтропия — величина аддитив­ная, она пропорц. числу ч-ц в систе­ме. Поэтому для систем с большим чис­лом ч-ц даже самое ничтожное относит. изменение энтропии, приходящейся на одну ч-цу, существенно меняет её абс. величину; изменение же энтропии, стоящей в показателе экспоненты в ур-нии (2), приводит к изменению вероятности W данного макросостоя­ния в огромное число раз. Именно этот факт явл. причиной того, что для системы с большим числом ч-ц следст­вия В. н. т. практически имеют не ве­роятностный, а достоверный хар-р. Крайне маловероятные процессы, со­провождающиеся сколько-нибудь за­метными уменьшениями энтропии, тре­буют столь огромных времён ожида­ния, что их реализация практически невозможна. В то же время малые ча­сти системы, содержащие небольшое число ч-ц, испытывают непрерывные флуктуации, сопровождающиеся лишь небольшим абс. изменением энтропии. Ср. значения частоты и величины этих флуктуации явл. таким же достовер­ным следствием статистич. термодина­мики, как и само В. н. т.

Буквальное применение В. н. т. к Вселенной как целому привело Клау­зиуса к неправомерному выводу о не­избежности «тепловой смерти» Все­ленной. И. М. Лифшиц.

• П л а н к М., Введение в теоретическую физику, ч. 5, М.— Л., 1935; Ландау Л.Д., Лифшиц Е. М., Статистическая физика, 3 изд., ч. 1, М., 1976; Смолуховский М., Границы справедливости второго начала термодинамики, пер. с нем., «УФН», 1967, т. 93, в. 4, с. 724.