Посвящен 75-летию развития системы образования Ленинградской области
| Вид материала | Реферат |
- Посвящен 75-летию развития системы образования Ленинградской области, 1967.83kb.
- Приказ №87 от 09. 10. 2011г. Концепция ресурсного центра «Мебельное производство» государственного, 384.98kb.
- Доклад о состоянии гражданской обороны муниципального образования Кировский муниципальный, 171.25kb.
- Конституцией Российской Федерации, федеральными закон, 318.73kb.
- Публичный отчет по результатам деятельности системы образования мо кировский район, 926.29kb.
- Отчёт главы администрации мо «Подпорожский муниципальный район Ленинградской области», 666.22kb.
- Фестиваль-конкурс посвящен Дню памяти благоверного князя Александра Невского. Фестиваль-конкурс, 21.31kb.
- Региональная целевая программа Информатизация системы образования Ленинградской области, 1115.91kb.
- Ленинградская область областной закон о дорожном фонде Ленинградской области, 28.21kb.
- Конституции Российской Федерации; Устава Ленинградской области; Устава муниципального, 33.14kb.
Приложение 6
Ирина Владимировна Иванова
Метод контроля остаточных знаний по математике
В среднем звене школы закладывается понятийный аппарат курса математики, на базе которого будут строиться в дальнейшем более сложные математические теории. Поэтому при изучении основных понятий курса математики необходимо знать, преобразуется ли информация, которую получает ученик, в прочные знания, основанные на долговременном запоминании, а не на оперативном.
Исходя из этого, учитель математики должен контролировать:
1) умения и навыки, которые обеспечивают применение изученных математических методов;
2) уровень сформированности понятийного аппарата изученных тем.
Первая задача может быть решена с помощью различных самостоятельных, проверочных, контрольных работ, тестов. Вторая задача отчасти решается на уроке устным опросом, тестированием, математическими диктантами при повторении пройденных тем. Однако, на мой взгляд, важно исследовать остаточные знания учащихся, т.е. тот объем понятий, который остался в памяти учащихся после изучения темы спустя некоторое время, в течение которого эти понятия с детьми не повторялись.
В своей работе по организации контроля за результатами обучения я использую метод ключевых определений, который позволяет оценить уровень знаний каждого учащегося с позиции его индивидуальных возможностей и способностей.
Объем и структура остаточных знаний связаны с интеллектуальным уровнем развития ученика. От ученика с низким уровнем интеллекта нельзя ожидать качественных и полных определений, которые вполне естественны для учащихся с высоким уровнем интеллекта. Поэтому вместе со школьным психологом определяем уровень интеллектуальных способностей по математике каждого учащегося.
Провожу самостоятельную работу, в которой предлагаю наиболее полно раскрыть основные понятия, составляющие суть диагностируемой темы. Содержание проверочной работы на 20 минут составляю из ключевых понятий темы, требующей самостоятельной мыслительной деятельности. При ответах на данные вопросы не требую дословного воспроизведения соответствующего материала из учебника, ответы учащиеся могут давать своими словами. Приведу пример такой работы по теме: «Уравнение с одной переменной.» (8 кл., сентябрь): 1. Что называется уравнением? 2. Что называется корнем уравнения? 3. Что значит решить уравнение? 4. Какие уравнения называются равносильными? 5. Сформулируйте свойства равносильности?
Качество выполнения каждого задания из работы оцениваю по 5-балльной системе, руководствуясь следующей схемой раскрытия понятий по их структуре: если понятие отделено от других понятий данной темы – 1 балл, если выявлены существенные признаки понятия – 3 балла, если указаны несущественные признаки – 1 балл. Максимальное число баллов за каждое определение – 5.
Считаю набранное число баллов. Вычисляю, сколько процентов задания выполнил ученик по формуле
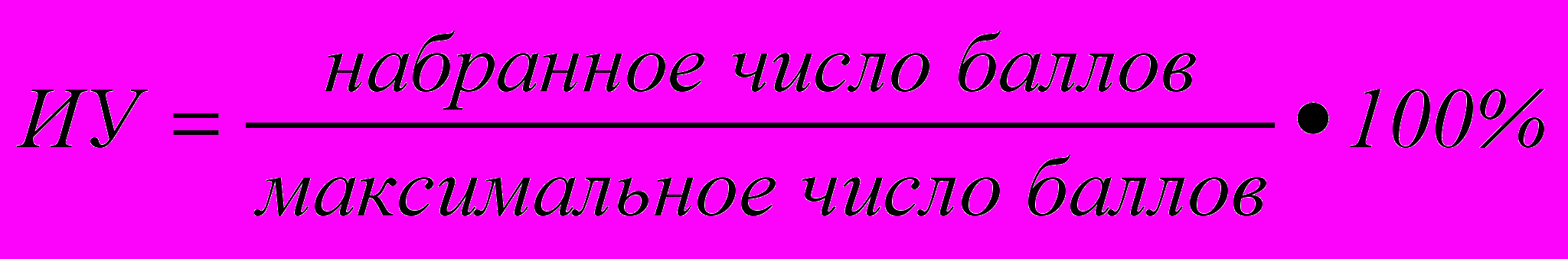
(ИУ – индивидуальный общий уровень знаний).
Нахожу, какая часть задания выполнена в среднем в классе по формуле
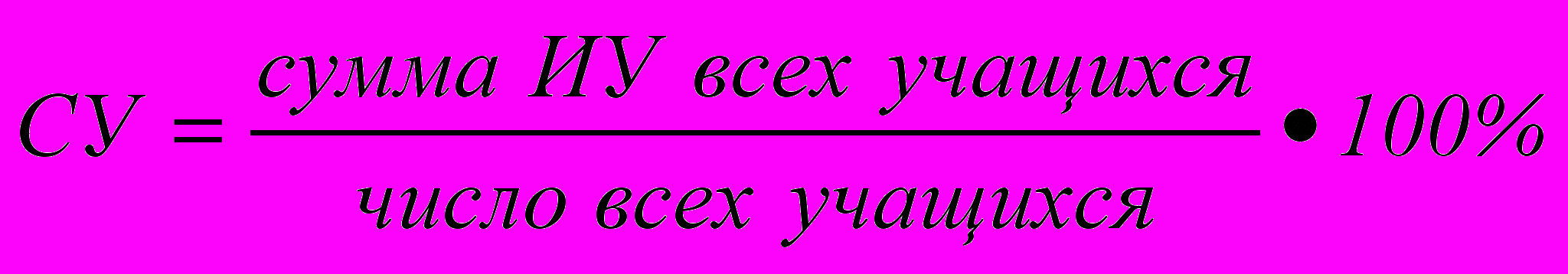
(СУ – средний общий уровень знаний).
На основе полученных данных вычисляю главный показатель – индивидуальное расхождение [1], т.е. тот процент выполненного задания, который соответствует уровню интеллекта каждого учащегося. Этот показатель определяет индивидуальную «недогруженность» каждого ученика и наибольший процент усвоенных понятий на нынешнем этапе умственного развития ученика.
Индивидуальное расхождение определяет оценку учащегося при проверке качества знаний.
Если ученик имеет высокий уровень интеллекта и при этом смог разъяснить всего 50% ключевых понятий, то значит нужно срочное восполнение качества знаний. Если же ученик имеет удовлетворительный уровень интеллекта и сумел разъяснить 60% заданных понятий, то он заслуживает отличной оценки.
Результаты такой работы оформляю в виде таблицы
| Ф.И. уч-ся | уровень интеллекта | объем задания | ндивид. расхожден. | оценки |
| 1. 2. 3. ….. | 1 3 3 ….. | 80% 100% 56% …. | 1 0 3 … | 4 5 3 …. |
Анализирую результаты, корректирую свою работу с учащимися. Группе учащихся, имеющих нулевой балл индивидуального расхождения, следует давать задания повышенного уровня сложности; с группой учащихся, имеющих индивидуальный балл расхождения 1, следует проводить работу по устранению пробелов; у учащихся, имеющих индивидуальный балл расхождения 3, недостаточно сформированы теоретические знания, т.е. работа идет на уровне оперативного запоминания, следует проводить работу по развитию мыслительной деятельности.
Такую работу по оценке уровня сформированности понятийного аппарата провожу на этапе предварительного контроля за знаниями учащихся с целью выбора соответствующих методов, приемов, форм работы для конкретного учащегося и класса в целом.
Считаю, что такая работа способствует развитию учащихся и формирует у них более прочные знания по математике.
Литература
1. Вербицкая Н., Бодряков В. Метод ключевых определений //Народное образование. – 1997. – № 10.
2. Вербицкая Н.О. и др. Метод контроля остаточных знаний по математике //Математика в школе. – 1998. – № 2.
