Лекция 5 по курсу «Линейная алгебра и аналитическая геометрия»

Вид материала

Лекция

Содержание Кривые второго порядка. Классификация кривых второго порядка B ≠ 0. Покажем, что при помощи поворота всегда можно избавиться от члена, содержащего смешанное произведение координат Bxy F′ свободный член: . Приравняем нулю коэффициенты при x′

Подобный материал:

• Линейная алгебра и аналитическая геометрия, 103.33kb.
• Лекции, час, 202.55kb.
• Рабочая программа дисциплины (модуля) «Линейная алгебра и аналитическая геометрия», 275.82kb.
• Рабочая программа учебной дисциплины линейная алгебра и аналитическая геометрия уровень, 426.51kb.
• Линейная алгебра и аналитическая геометрия (Все, что доказывалось на лекциях — доказывать), 35.13kb.
• Рабочая программа учебной дисциплины ен. Ф. 01. Аналитическая геометрия и линейная, 148.75kb.
• Учебно-методический комплекс учебной дисциплины ен. Ф. 01 Математика (аналитическая, 542.76kb.
• Программа курса :«Линейная алгебра и аналитическая геометрия», 38.96kb.
• Вопросы к зачету по математике для направления «Сервис» по разделу «Линейная алгебра, 22.33kb.
• Учебно-методический комплекс для специальности 080111 Маркетинг Москва 2009, 497.47kb.

Лекция 5 по курсу «Линейная алгебра и аналитическая геометрия»


5. Кривые и поверхности второго порядка, собственные векторы матриц


Кривые второго порядка


ky.narod.ru/library.htm


В предыдущих лекциях мы изучали прямые линии и плоскости, они задаются уравнениями первой степени: ax + by + cz + d = 0. Сегодня мы узнаем, какие линии на плоскости описываются уравнением второго порядка


Ax² + Bxy + Cy² + Dx + Ey + F = 0. (1)


Для начала мы изучим эллипс, гиперболу и параболу, которые получаются в результате сечения кругового конуса плоскостями, не проходящими через его вершину. Эллипс получается, если секущая плоскость пересекает все образующие одной полости конуса (рис. 1, а); гипербола – если секущая плоскость пересекает обе полости конуса (рис. 1, б); парабола получается, если секущая плоскость параллельна одной из образующих конуса (рис. 1, в). В конце лекции мы покажем, что этими тремя линиями и линейными образами (то есть, прямыми) исчерпываются все линии, определяемые уравнениями второй степени.





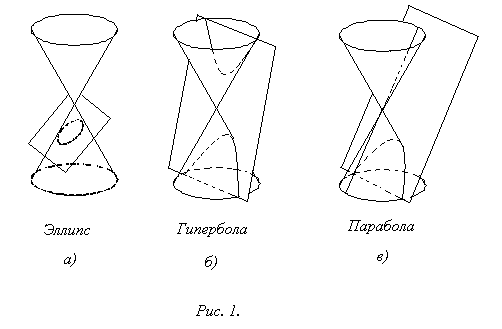
Эллипс


Определение 1. Эллипсом называется геометрическое место точек плоскости, для к
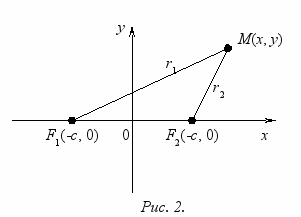
оторых сумма расстояний до двух фиксированных точек этой плоскости, называемых фокусами, есть величина постоянная.


Пусть F₁ и F₂ – фокусы. Выберем начало координат в середине отрезка F₁F₂. Ось Ox направим по отрезку F₁F₂, а Oy перпендикулярно вверх. Пусть 2c – длина отрезка F₁F₂, если c = 0, то F₁ совпадает с F₂ и мы получаем окружность. В этой системе координат фокусы имеют координаты F₁(-с, 0), F₂(с, 0). Обозначим через r₁ и r₂ расстояния от фокусов F₁ и F₂ до точки M на эллипсе, а через 2a постоянную сумму этих расстояний. Тогда условием того, что точка M принадлежит эллипсу, будет равенство


r₁ + r₂ = 2a. (2)


Нас будет интересовать случай, когда 2a > 2c, так как если 2a = 2c, то эллипс вырождается в отрезок F₁F₂. Найдем значения r₁ и r₂:


, .


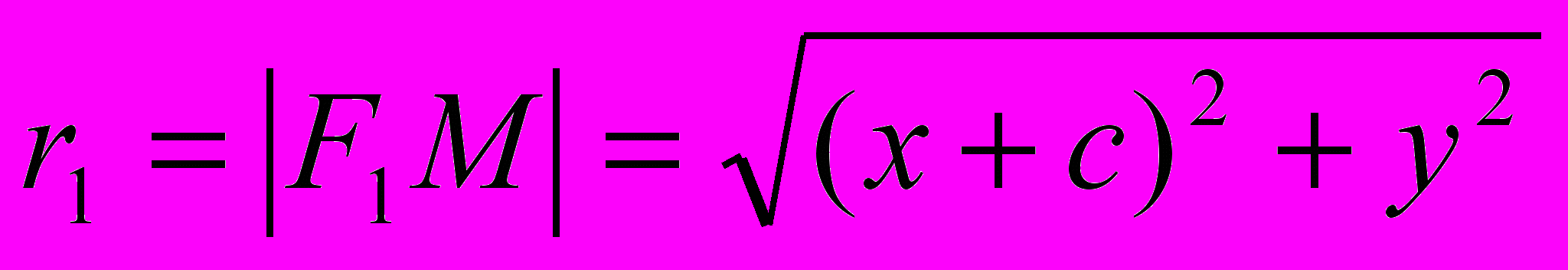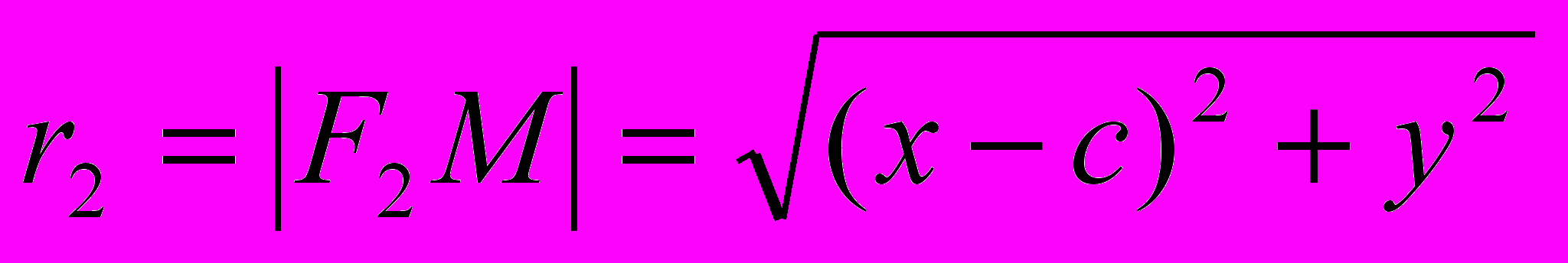Тогда условие (2) примет следующий вид:


.


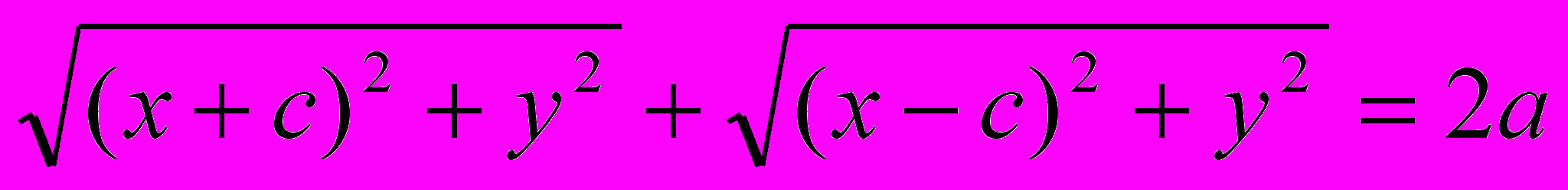Перенесем первый корень в правую часть:





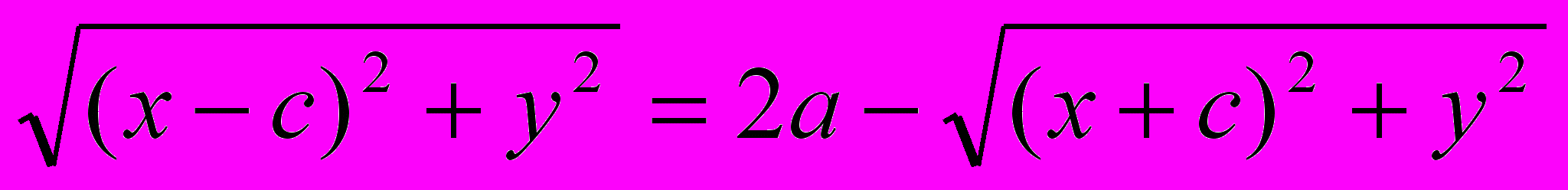
и возведем обе части полученного равенства в квадрат:


.


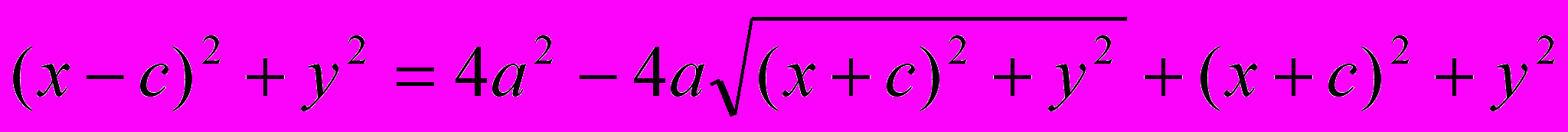Выразим из последнего равенства корень:







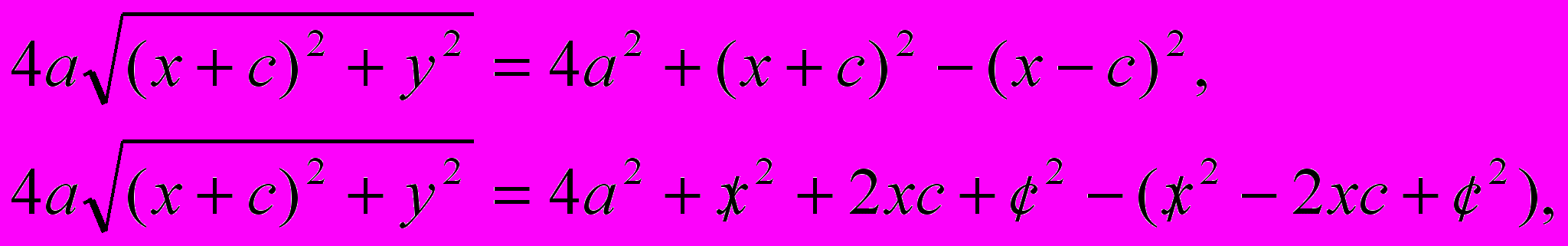
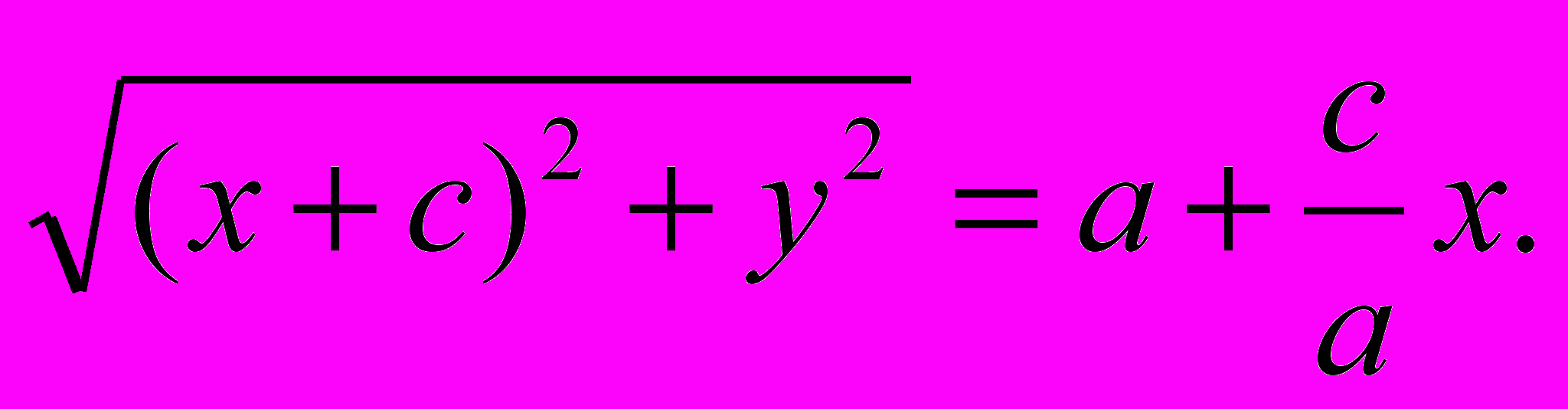
Возведем обе части последнего равенства в квадрат:


.


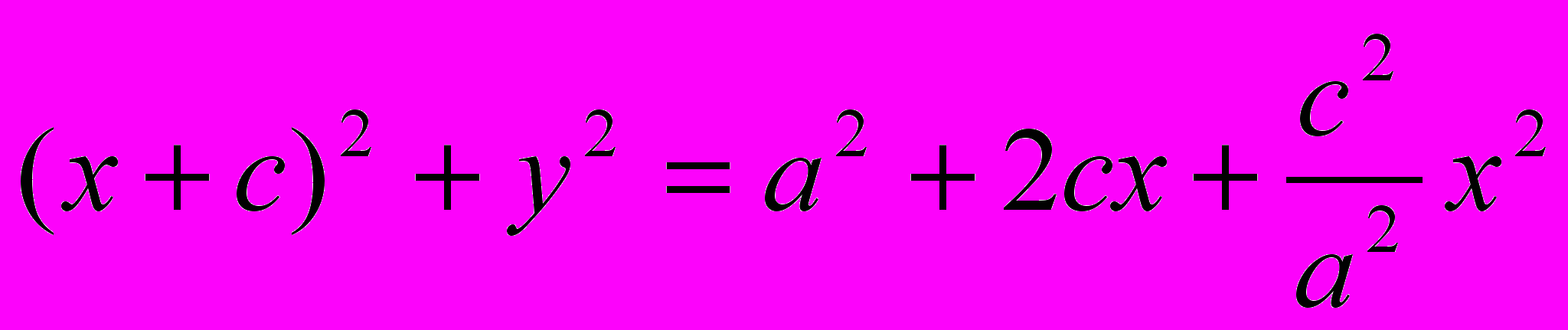Раскроем скобки и приведем подобные слагаемые:





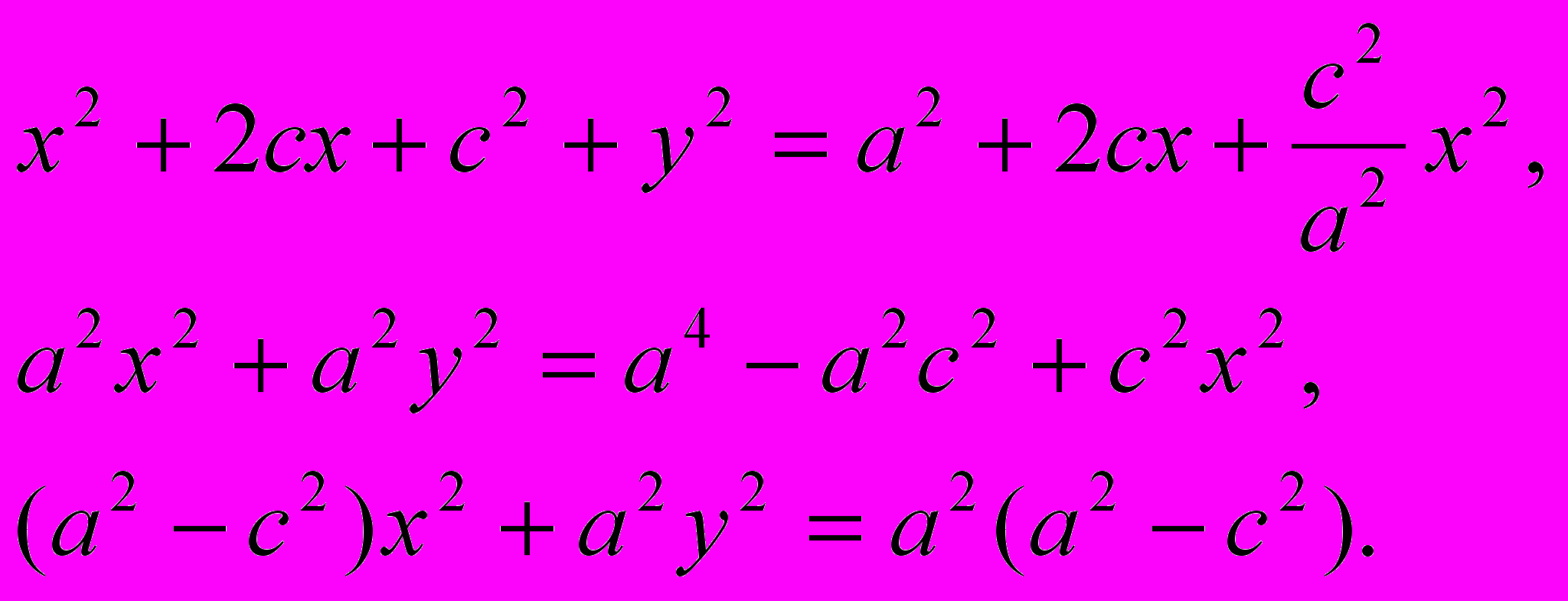
Так как 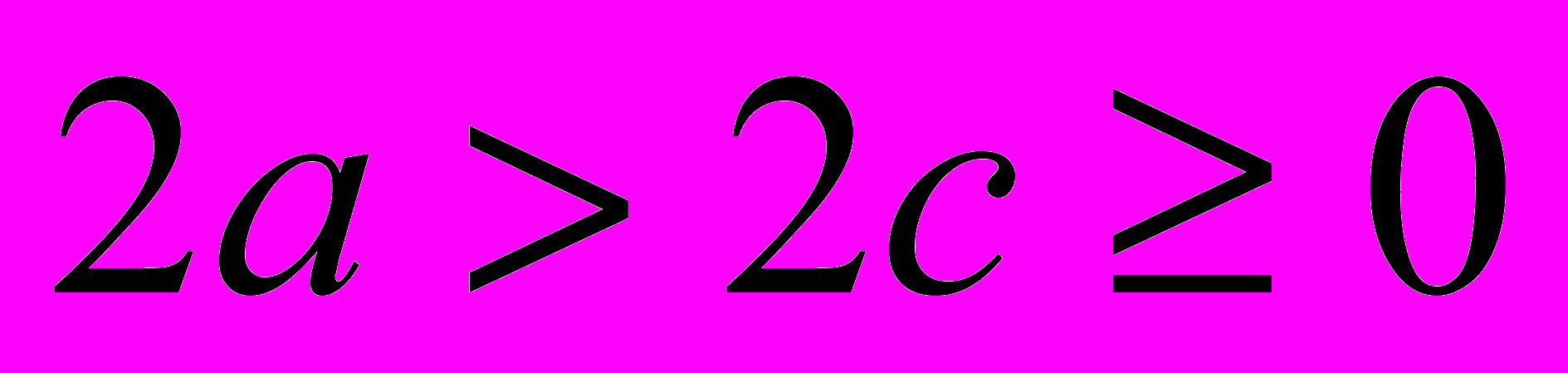, то разность a² – c² > 0, обозначим ее через b² = a² – c². Последнее равенство примет вид


b² x² + a² y² = a² b².


Разделив на a²b², получим каноническое уравнение эллипса:


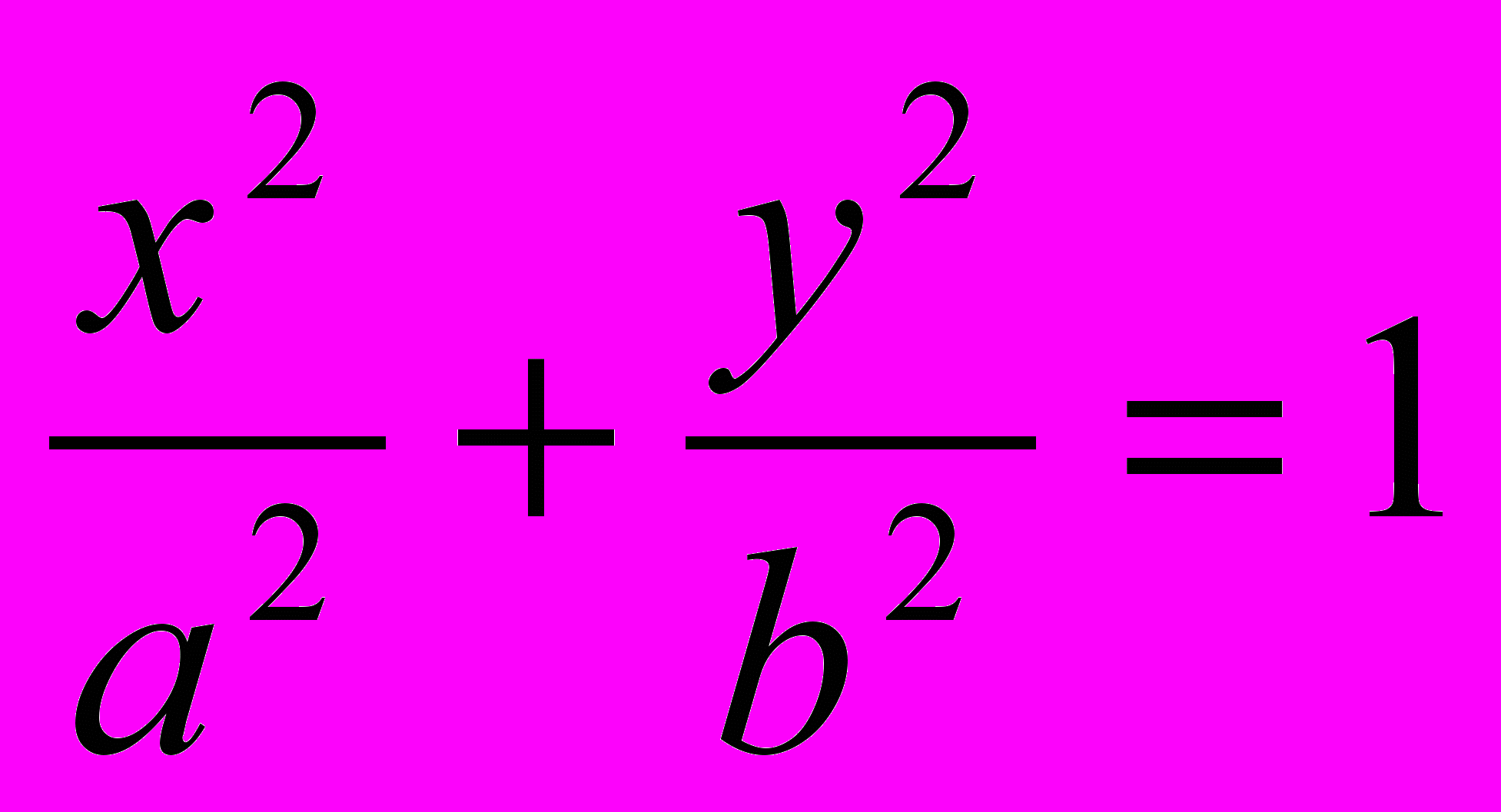. (3)


Замечание 1. Мы взяли точку на эллипсе и показали, что ее координаты удовлетворяют уравнению (3). Но при возведении в квадрат уравнение могло приобрести лишние корни. Можно проверить, что любая точка плоскости, координаты которой удовлетворяют уравнению (3), лежит на эллипсе.




При x = 0 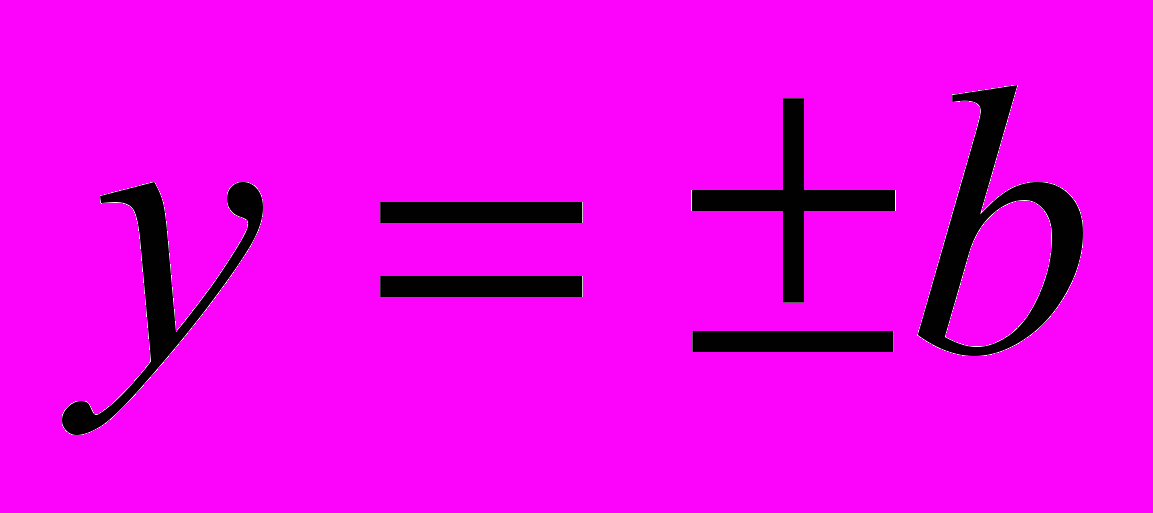, при y = 0 .


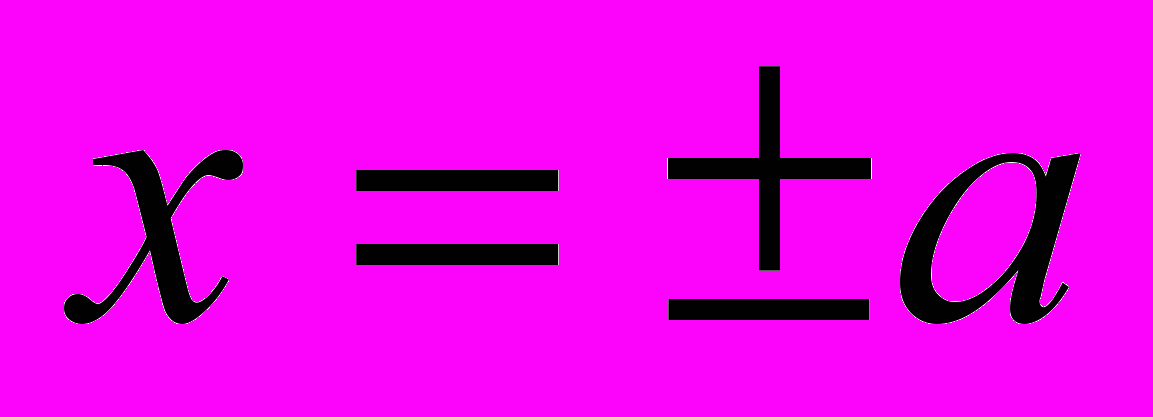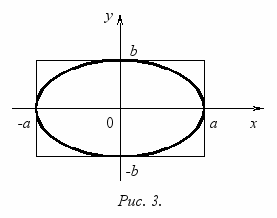
Определение 2. Величины a и b называют большой и малой полуосями эллипса соответственно.


Гипербола


Определение 3. Гиперболой называется геометрическое место точек плоскости, для которых абсолютная величина разности расстояний до двух фиксированных точек этой плоскости, называемых фокусами, есть величина постоянная.


Как и в случае эллипса, обозначим фокусы F₁ и F₂. Расстояние между ними через 2c, а постоянную абсолютную величину разности расстояний r₁ и r₂ от фокусов до гиперболы через 2a. Но в этом случае 2a < 2c, так как разность двух сторон треугольника меньше его третьей стороны. Условием того, что точка M принадлежит гиперболе, будет равенство


|r₁ – r₂| = 2a. (4)

Или в координатной записи:


.


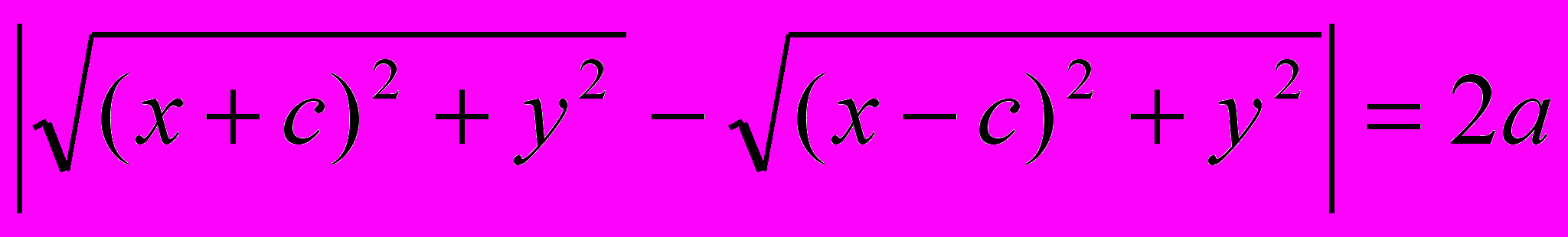Избавляясь от корней, так же как в случае эллипса, получим каноническое уравнение гиперболы:

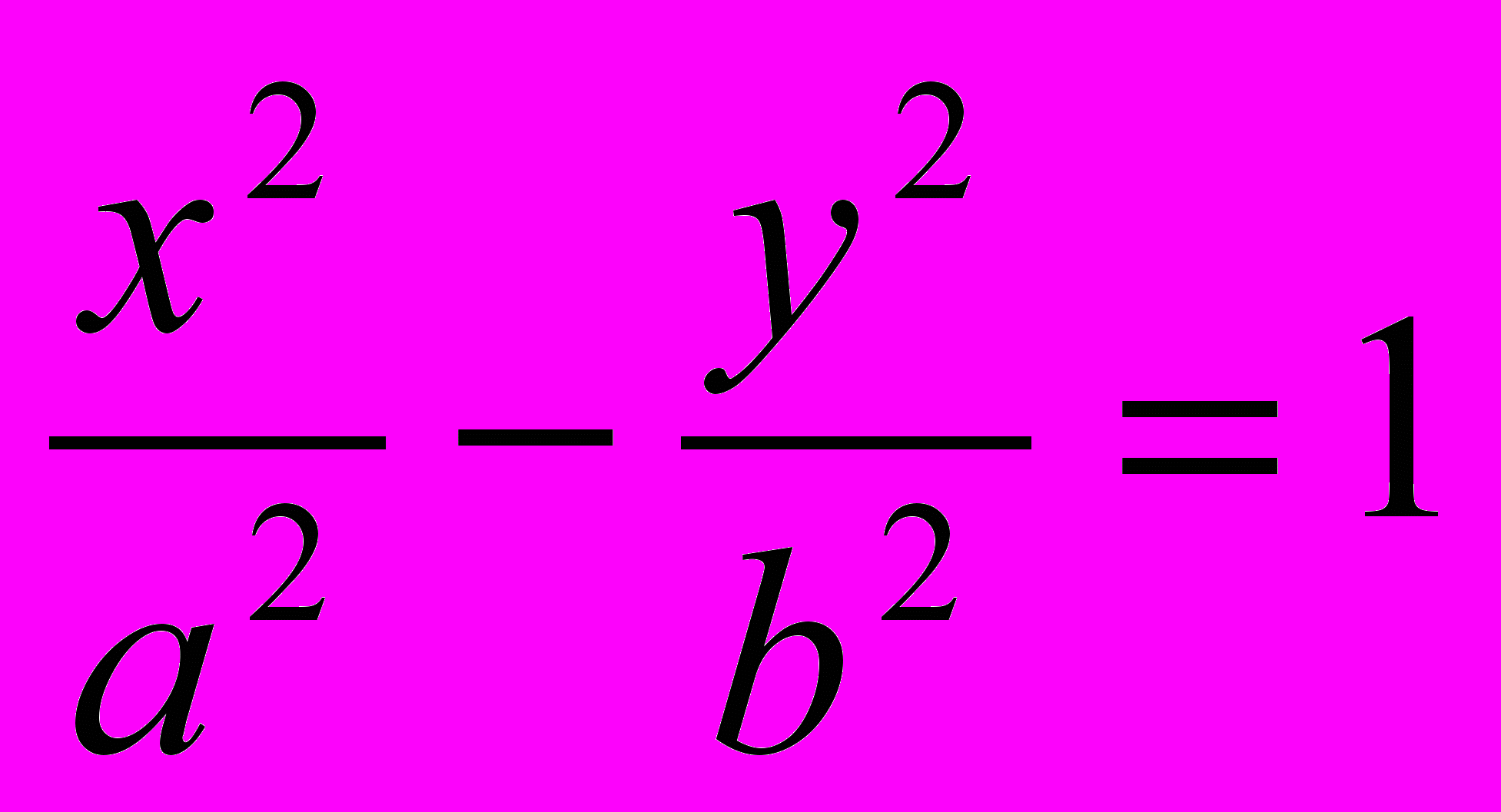, (5)

где b² = c² – a².


При y = 0 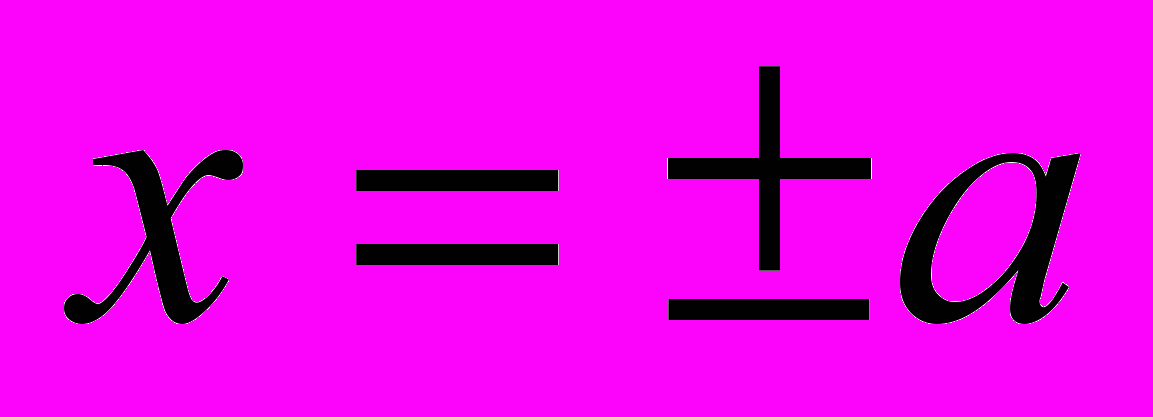, а при x = 0 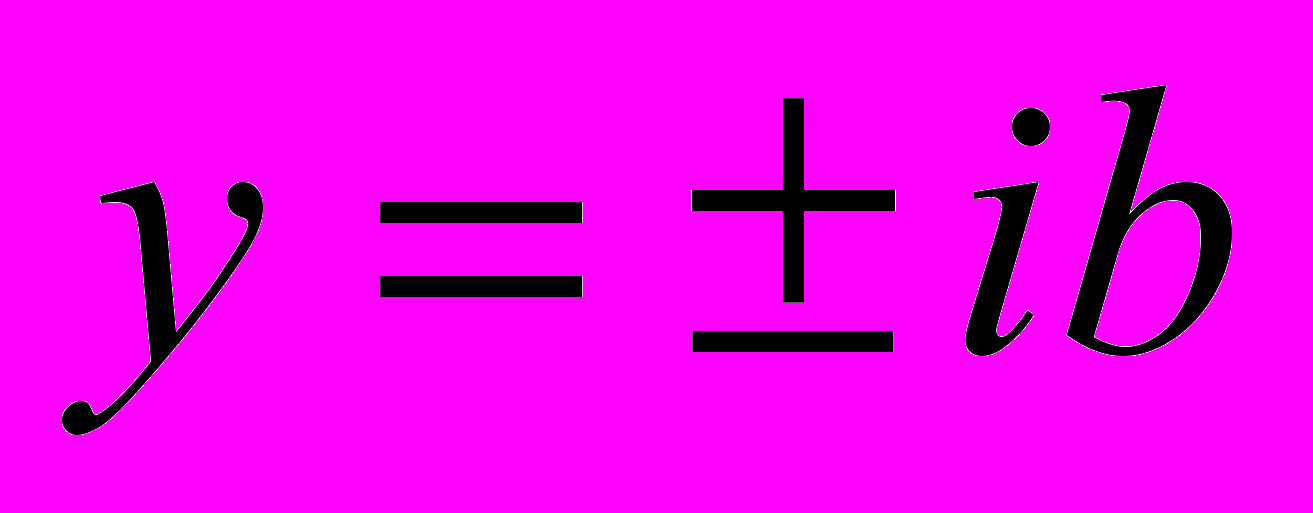, то есть оси Oy гипербола не пересекает.


Определение 4. Величина a называется действительной полуосью гиперболы, а b – мнимой.


П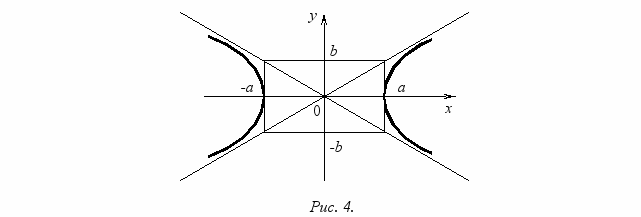рямые 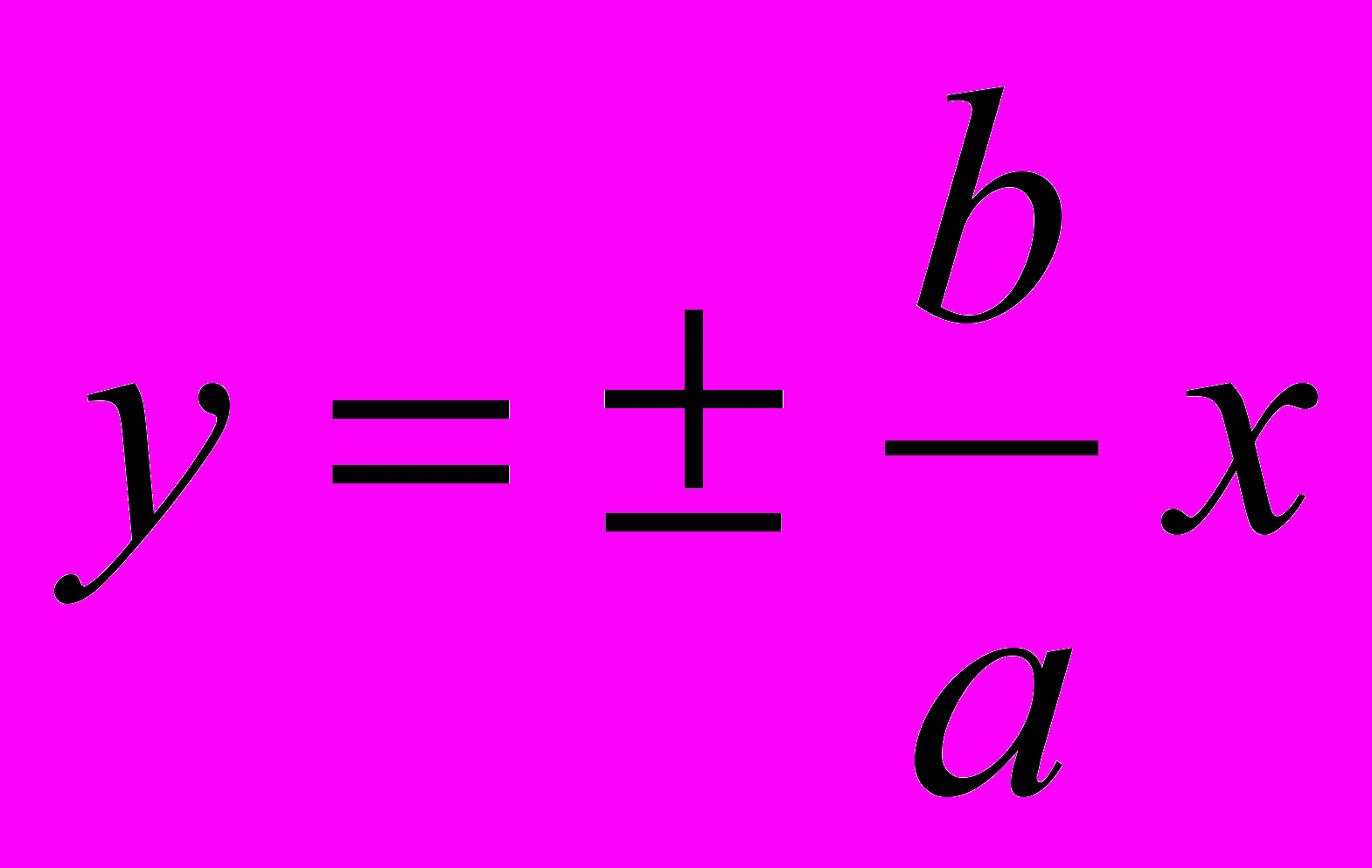являются асимптотами гиперболы, то есть такими прямыми, что расстояние от гиперболы до них стремится к нулю, при возрастании x.




Если в уравнении (5) справа стоит -1, то есть


,


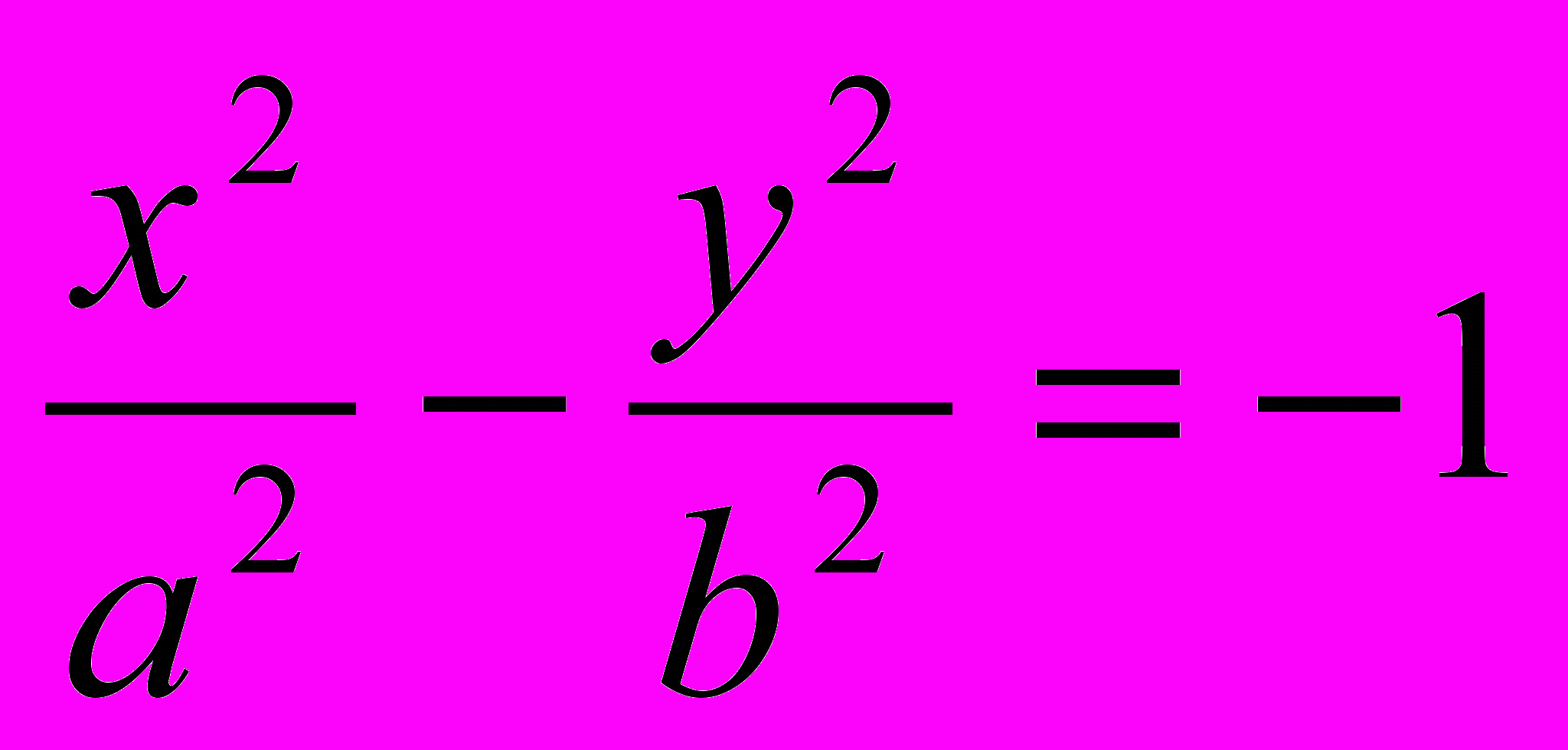то, переписав его в виде


,


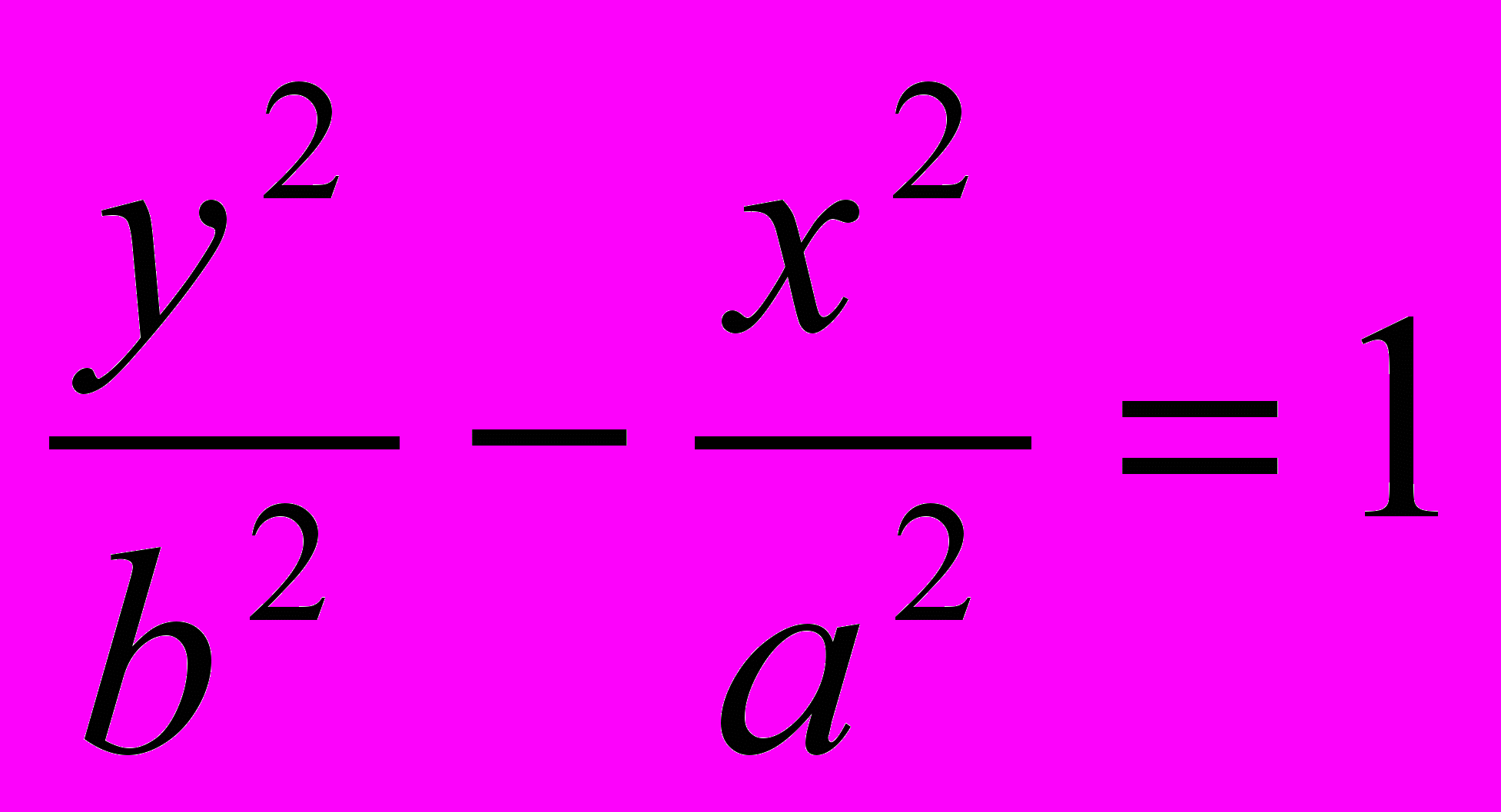мы видим, что координаты как бы меняются местами. Это уравнение сопряженной гиперболы (рис. 5).

Парабола


Определение 5. Параболой называется геометрическое место точек плоскости, для которых расстояние до некоторой фиксированной точки этой плоскости равно расстоянию до некоторой фиксированной прямой, лежащей в той же плоскости. Указанная точка называется фокусом, а прямая – директрисой параболы.




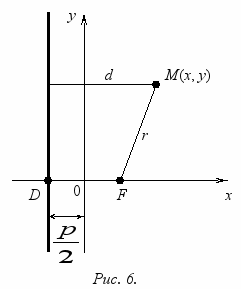
Мы будем рассматривать случай, когда фокус не лежит на директрисе, иначе, парабола выродилась бы в прямую перпендикулярную директрисе. Обозначим через p расстояние от фокуса F до директрисы. Выберем начало координат в середине отрезка FD, представляющего собой перпендикуляр, опущенный из фокуса F на директрису. Ось Ox направим по отрезку DF, а ось Oy перпендикулярно вверх. Тогда фокус F будет иметь координаты 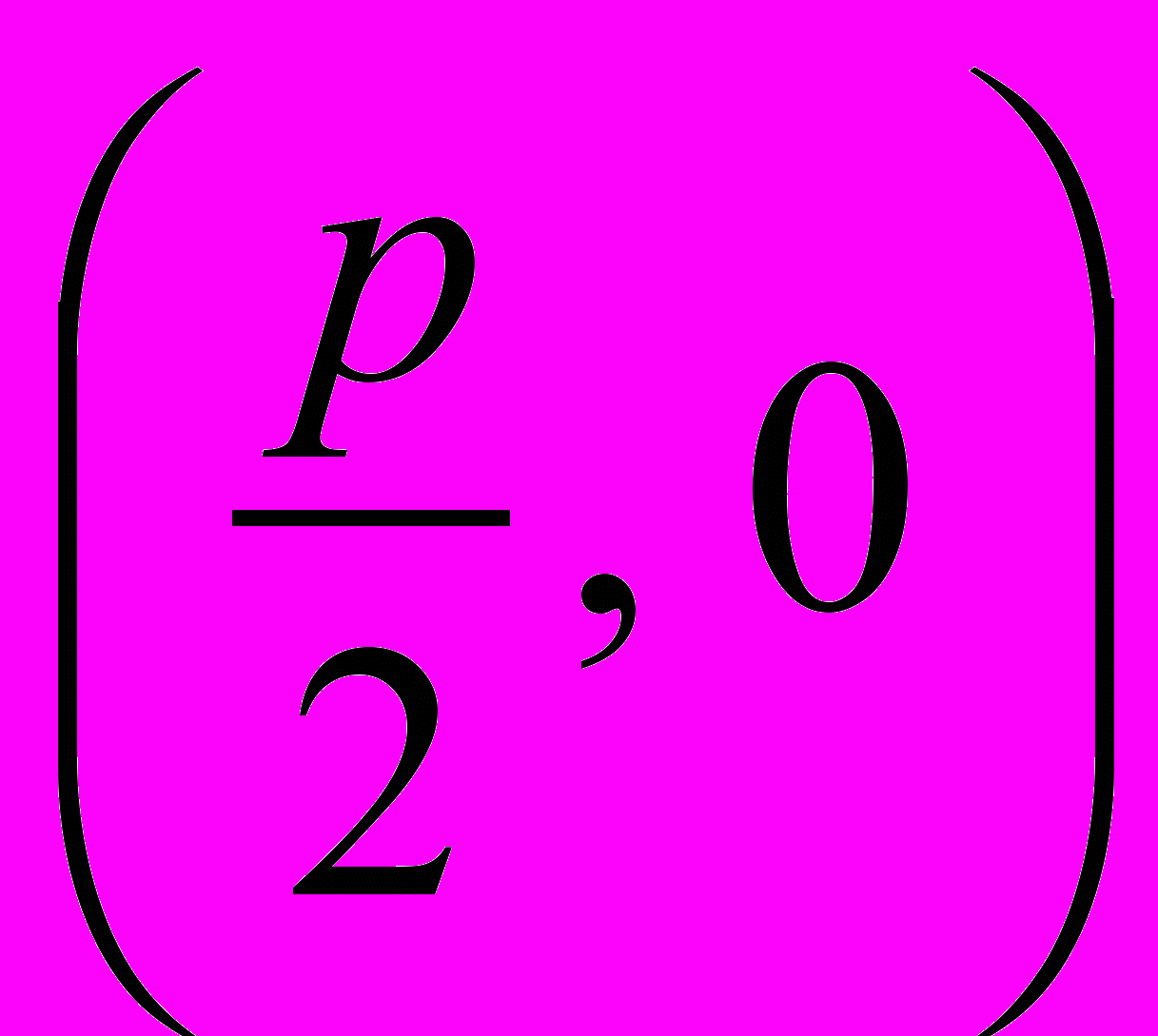, и расстояние r от фокуса до произвольной точки на плоскости M(x, y) будет равняться 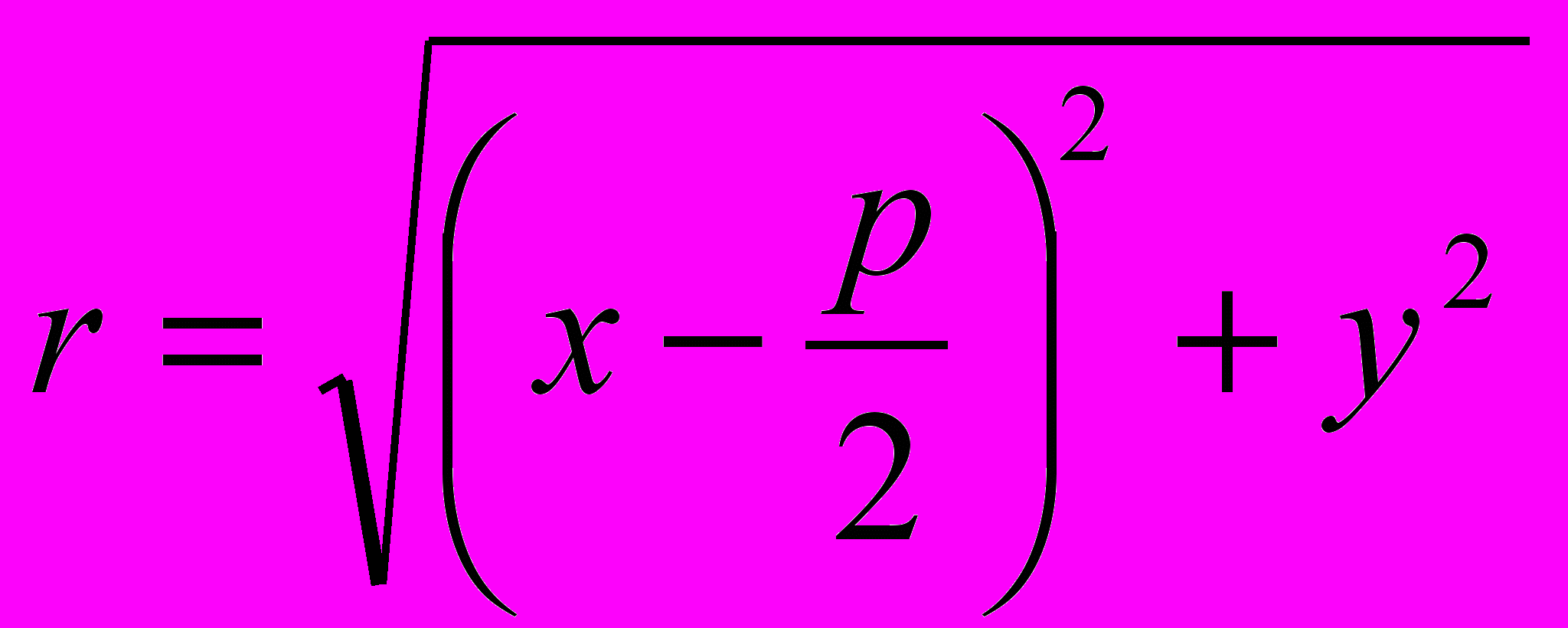, а расстояние d от точки M(x, y) до директрисы 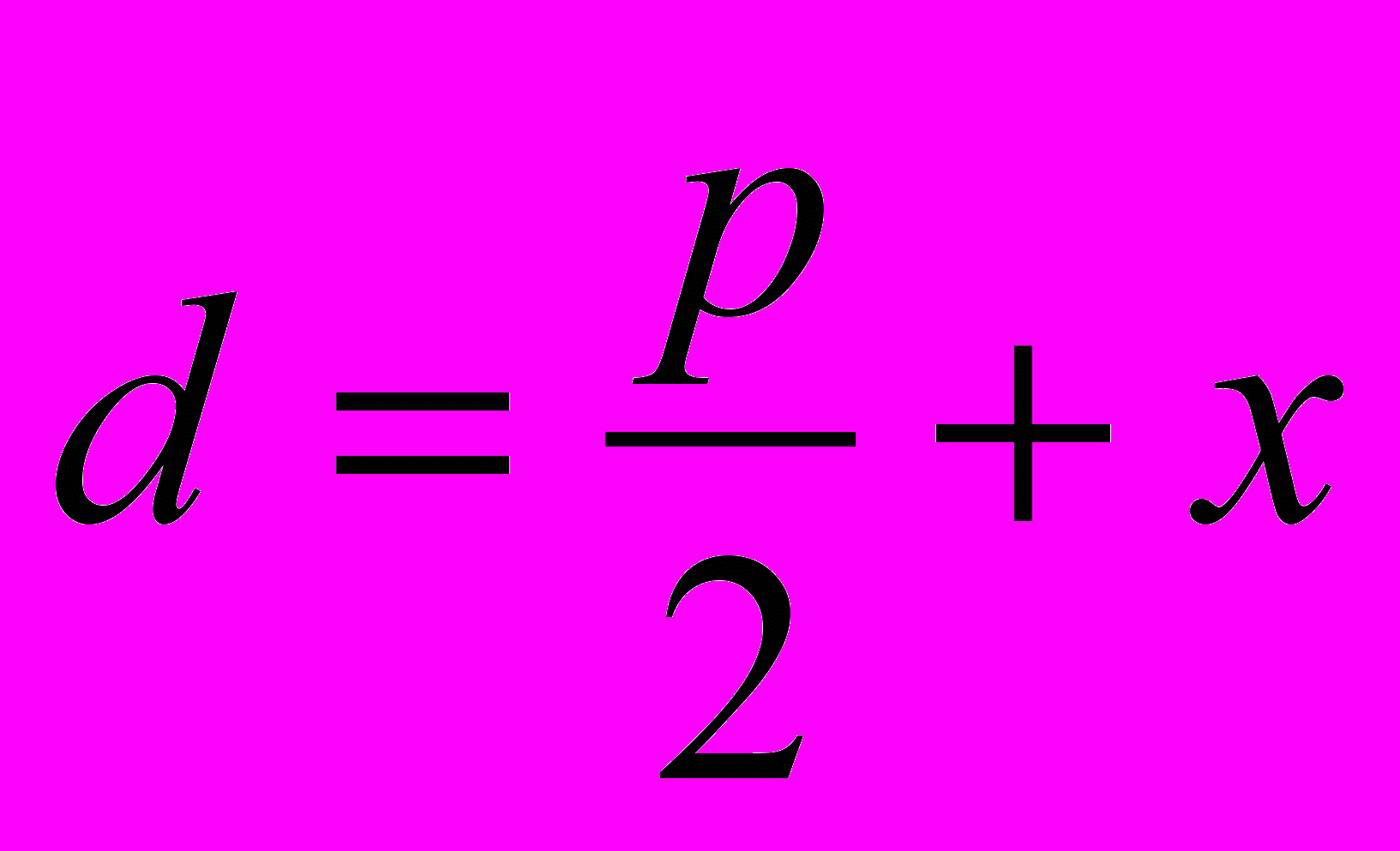. Условие принадлежности точки M(x, y) параболе запишется в виде

r = d. (6)


Или в координатной форме:

.


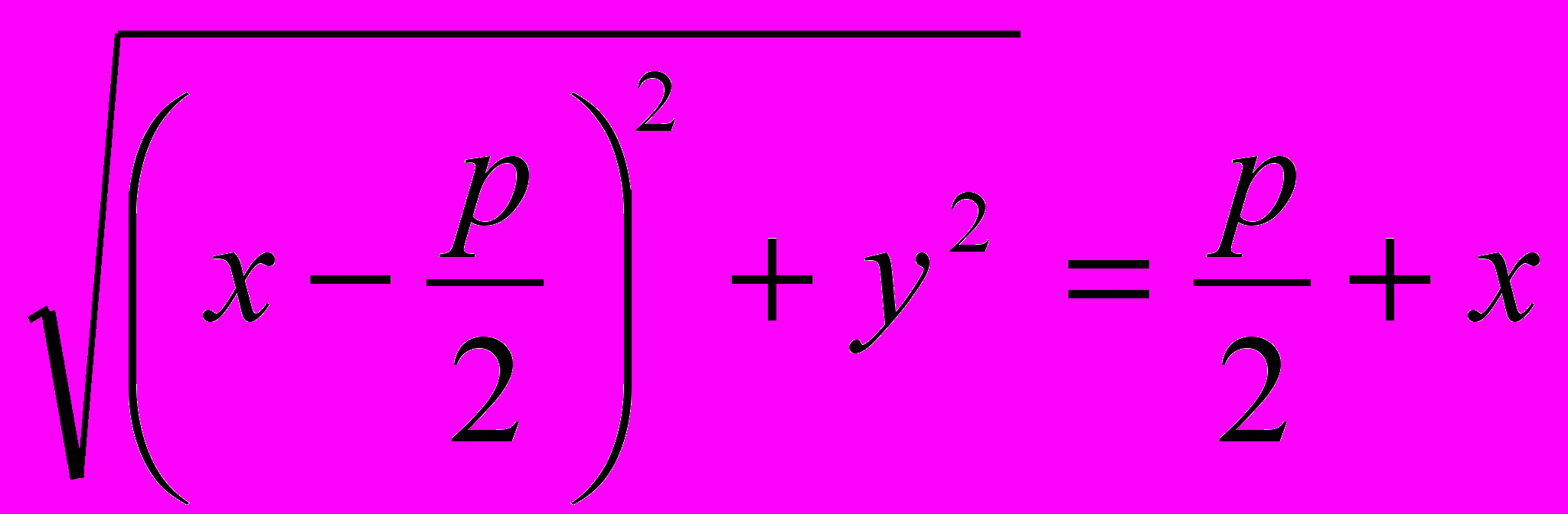Избавляясь от корня, получим каноническое уравнение параболы:


y² = 2px. (7)


Число p называется параметром параболы. Если p < 0, то парабола лежит слева от директрисы (x переходит в -x).


Уравнения эллипса, гиперболы и параболы в полярных координатах




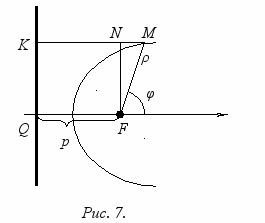
Для точки параболы отношение расстояния до фокуса к расстоянию до директрисы равно единице. Для эллипса отличного от окружности и гиперболы можно указать такие прямые, называемые директрисами, что отношение расстояний до фокуса к расстоянию до директрисы, соответствующей фокусу, есть постоянная величина, которую мы обозначим через e. Выберем начало полярной системы координат (ρ, φ) в фокусе F. Обозначим через p расстояние от фокуса до директрисы. Отношение 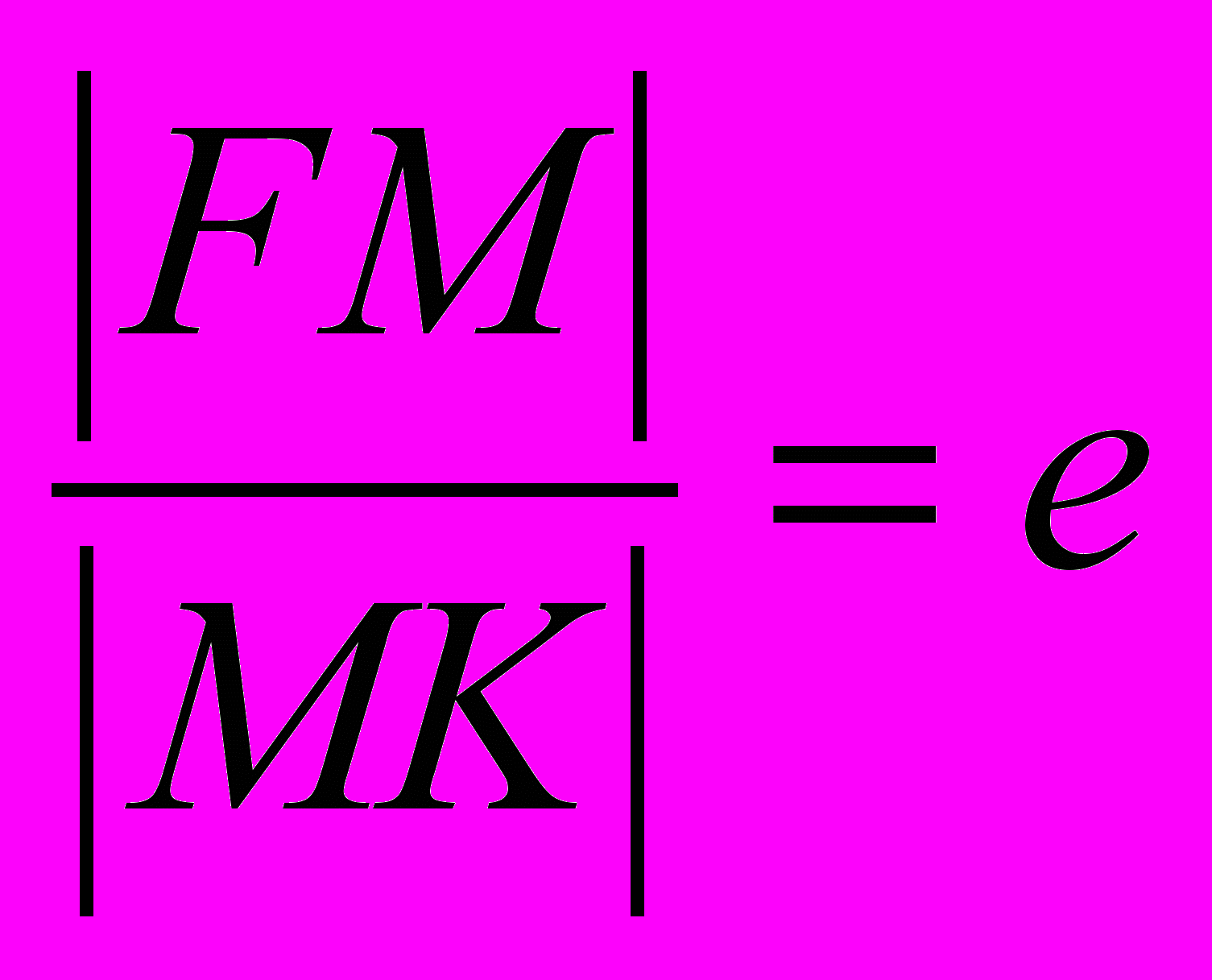, , 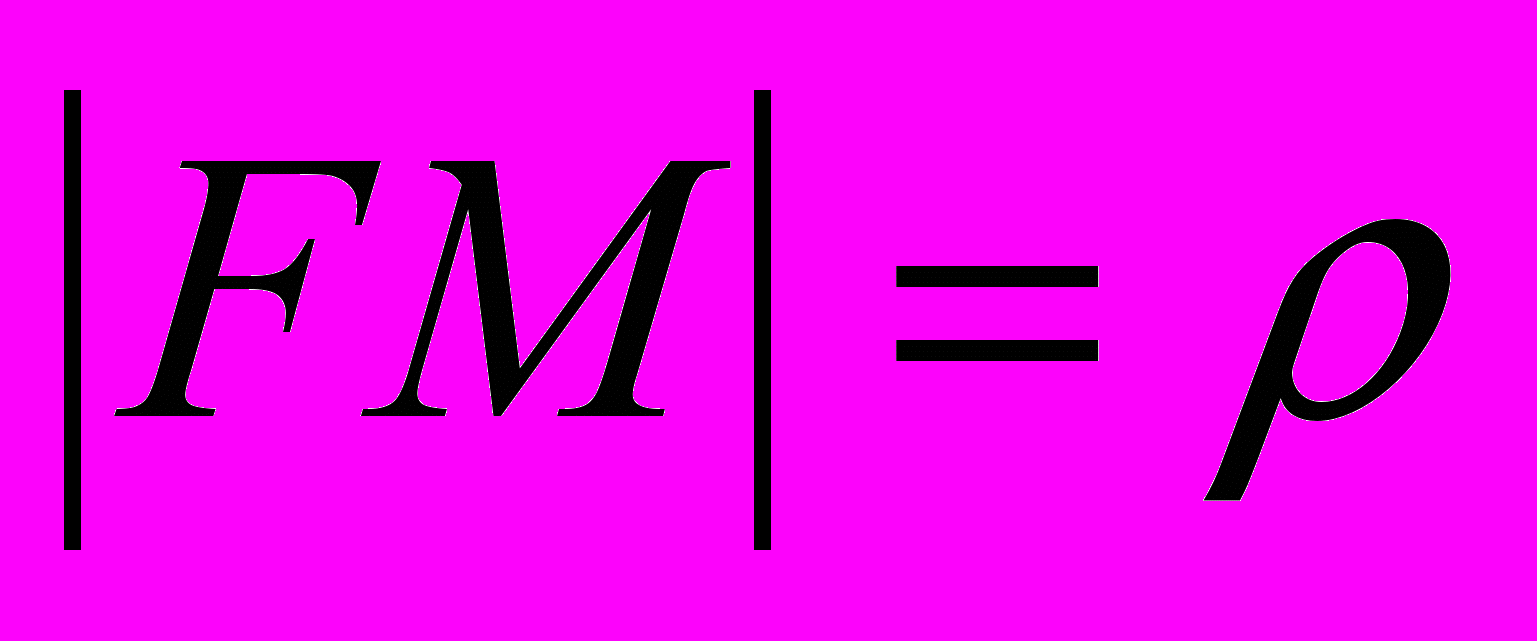а 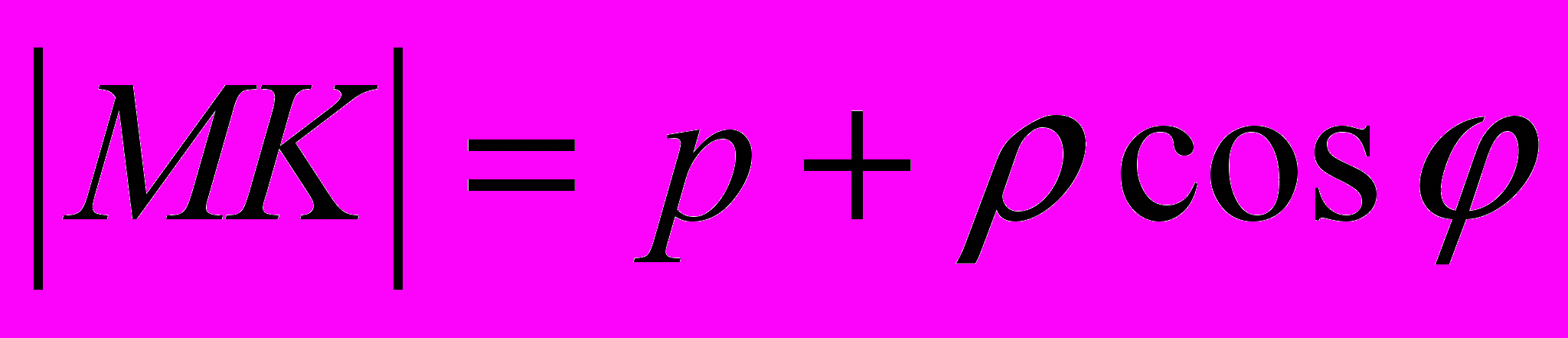. Отсюда получаем, что

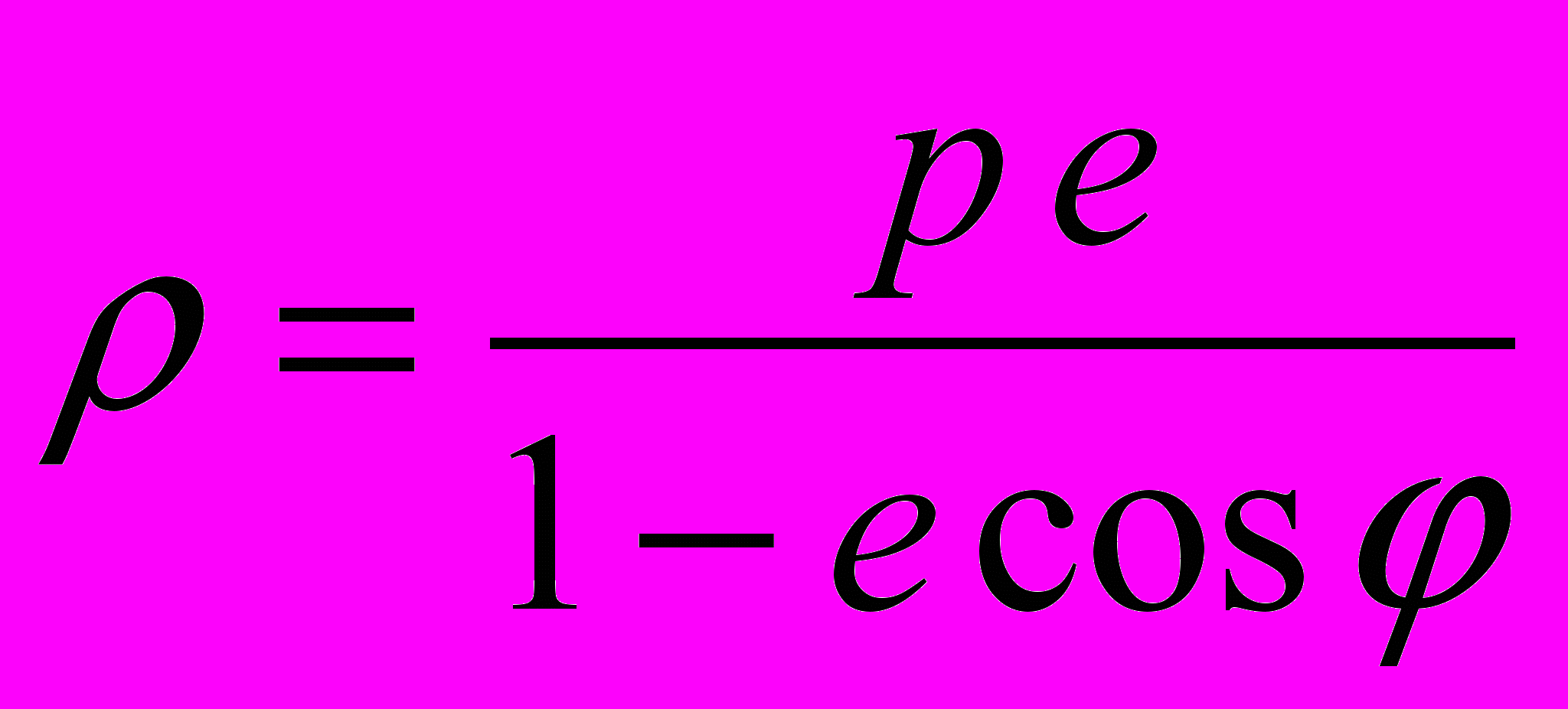. (8)

Для эллипса 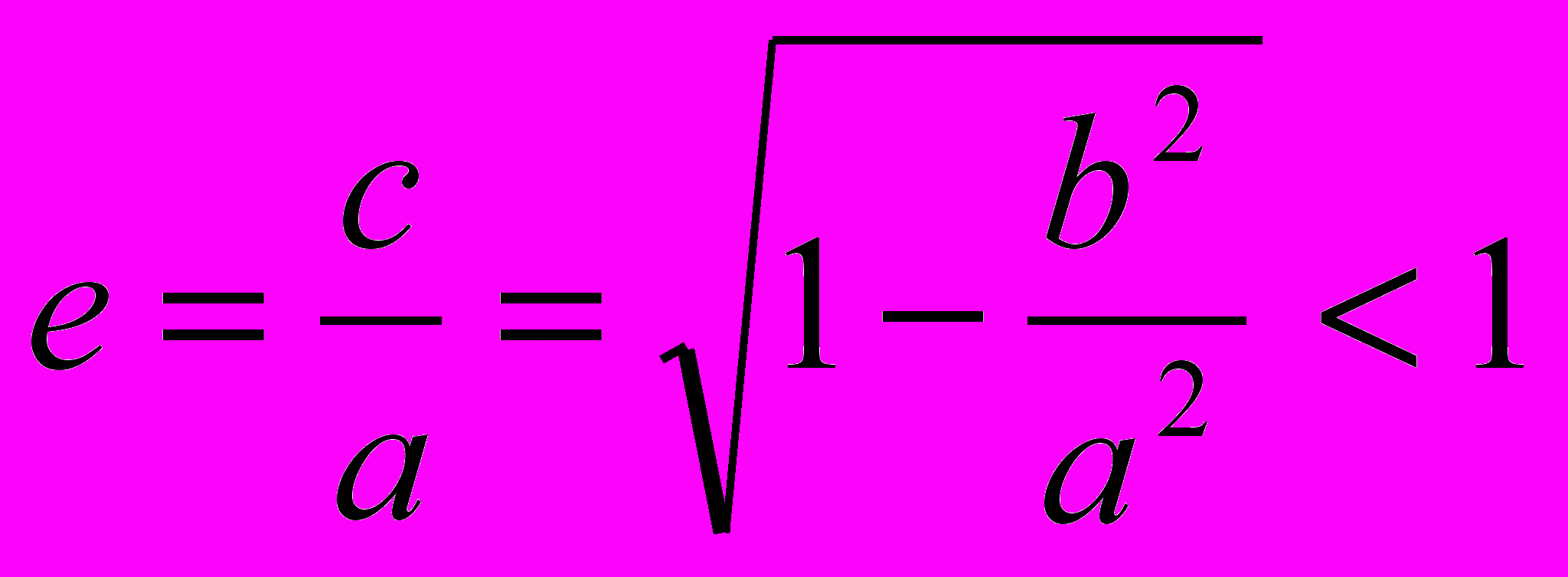, а для параболы e = 1. Таким образом, уравнение (8) является уравнением эллипса при e < 1 и уравнением параболы при e = 1 в полярных координатах. Для гиперболы 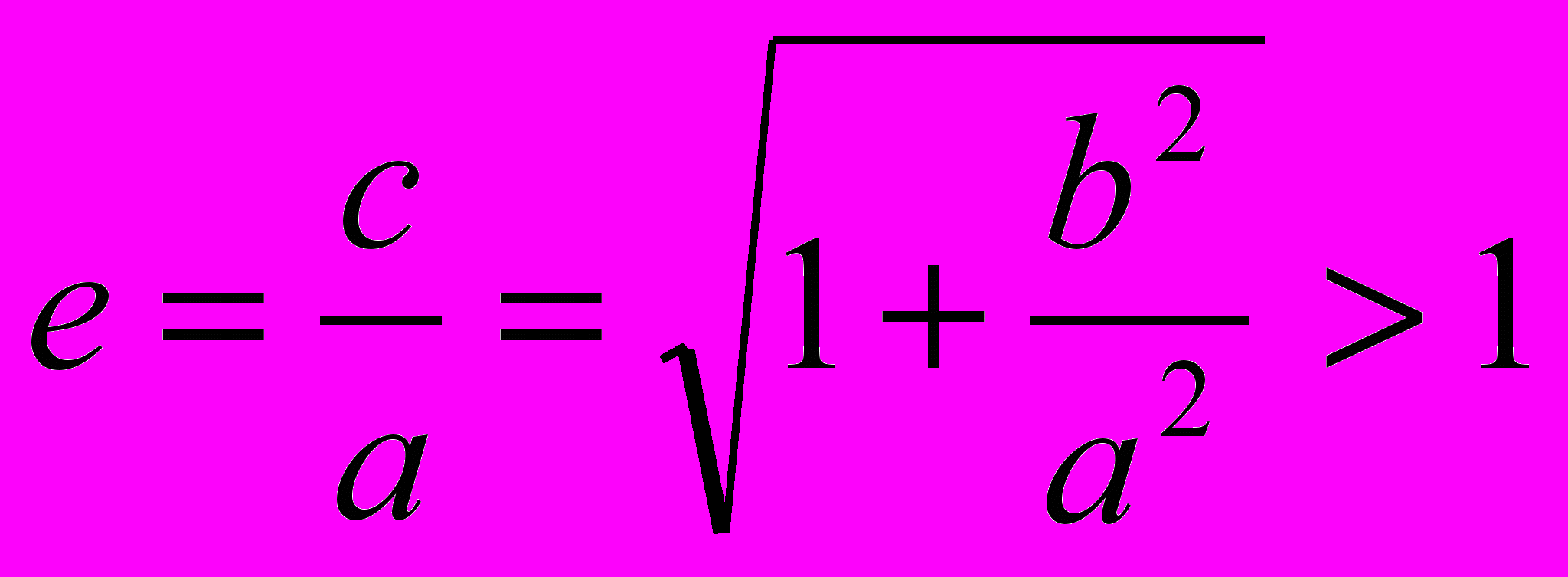, но она имеет две ветви, так что ее уравнение в полярных координатах имеет вид:


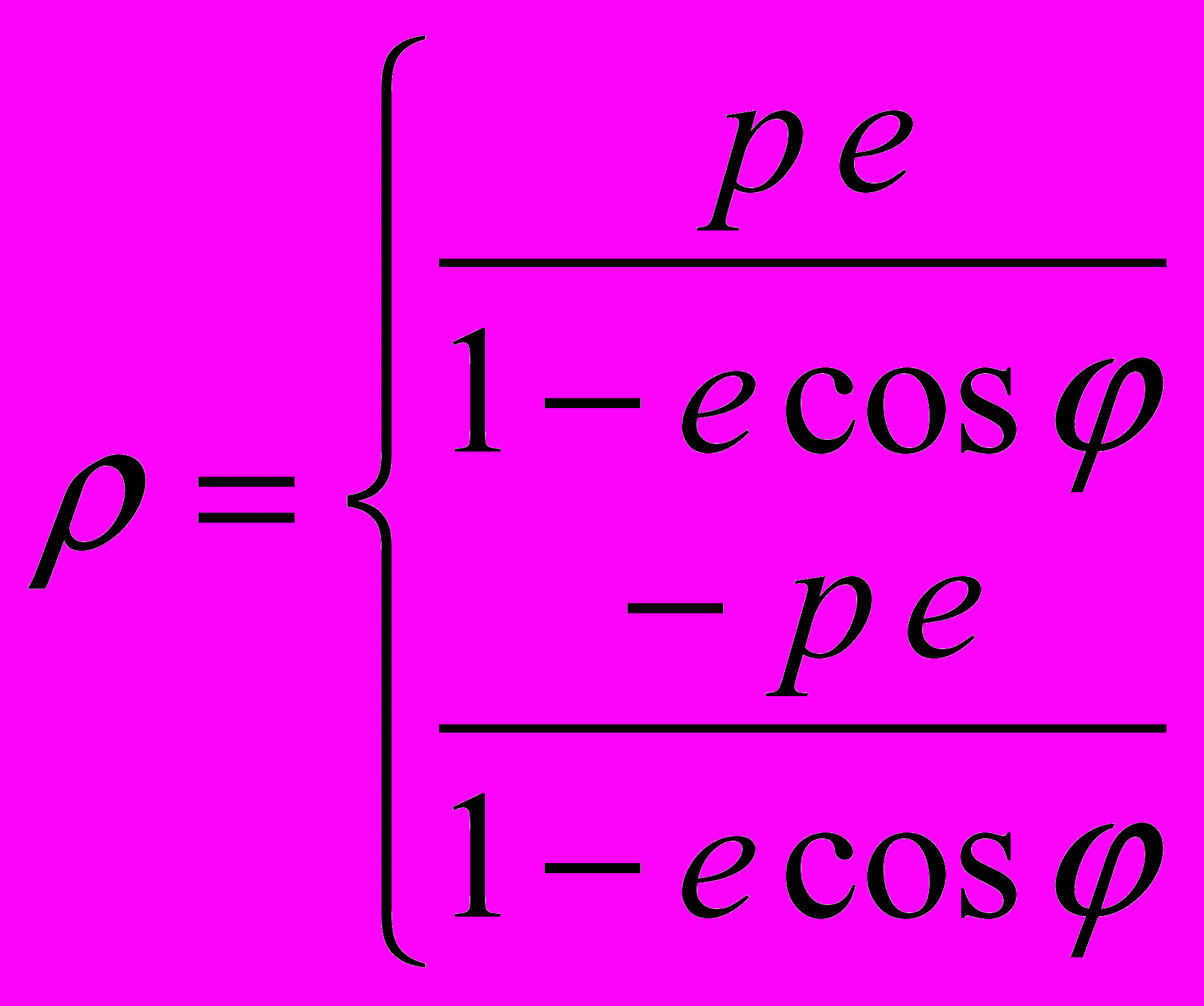, e > 1. (9)


Наиболее просто в полярных координатах выглядит уравнение окружности:


ρ = R. (10)


Уравнения директрис для эллипса и гиперболы имеют вид 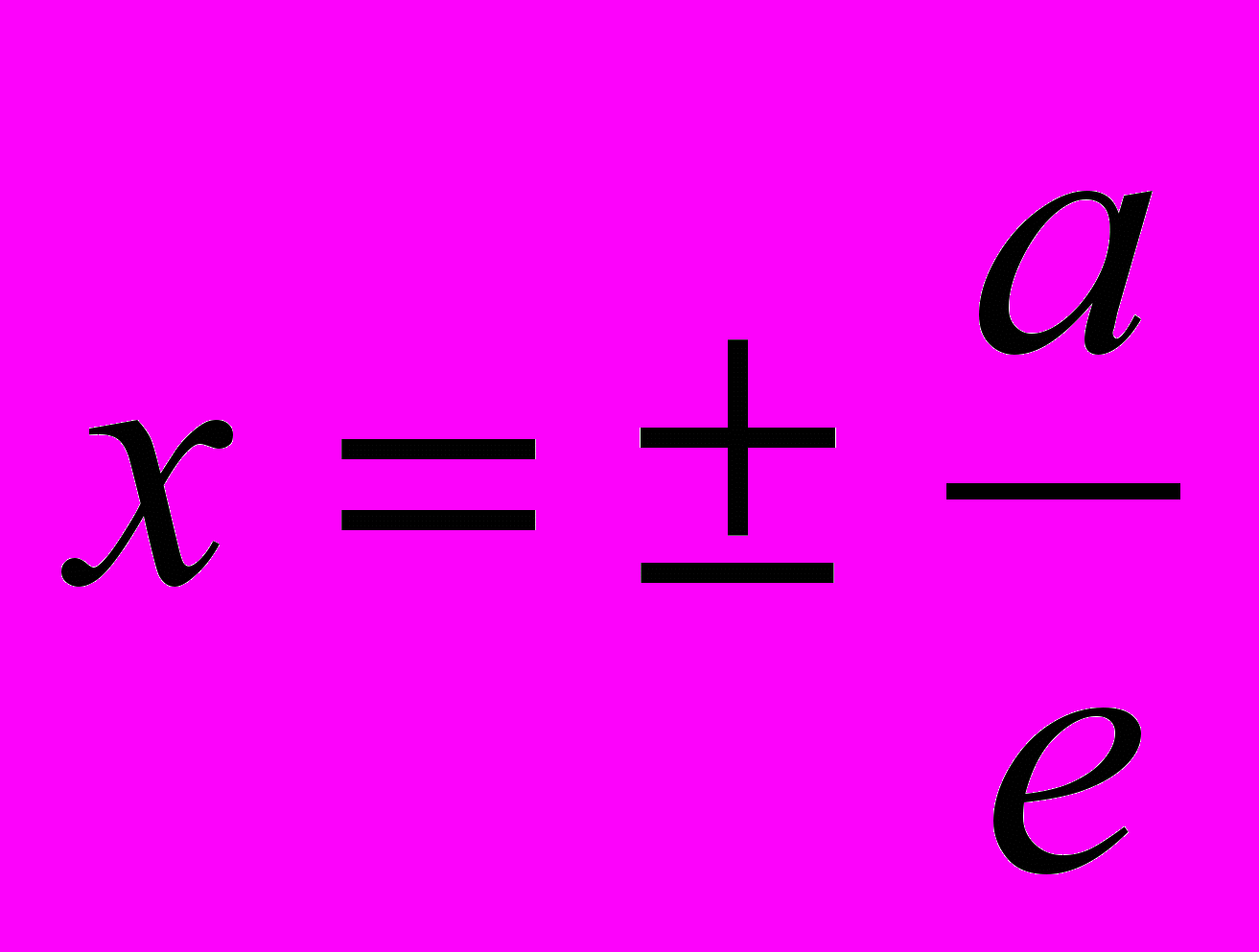. То есть, эллипс директрисы пересекают, а гиперболу – нет.


^ Кривые второго порядка. Классификация кривых второго порядка


Теорема 1. Если в некоторой декартовой прямоугольной системе координат линия задается алгебраическим уравнением степени n, то в любой другой декартовой прямоугольной системе координат уравнение линии будет иметь такой же вид и порядок.


Преобразованиями, которые переводят декартову прямоугольную систему координат xOy в другую декартову прямоугольную систему координат x′Oy′, являются поворот осей и перенос начала координат. Рассмотрим уравнение (1), при A² + B² + C² ≠ 0, и попробуем привести его к наиболее простому виду.

Предположим, что ^ B ≠ 0. Покажем, что при помощи поворота всегда можно избавиться от члена, содержащего смешанное произведение координат Bxy. После поворота осей на угол φ старые координаты связаны с новыми формулами


x = x′ cos φ – y′ sin φ,

y = x′ sin φ + y′ cos φ.


Перепишем уравнение (1) в новых координатах:





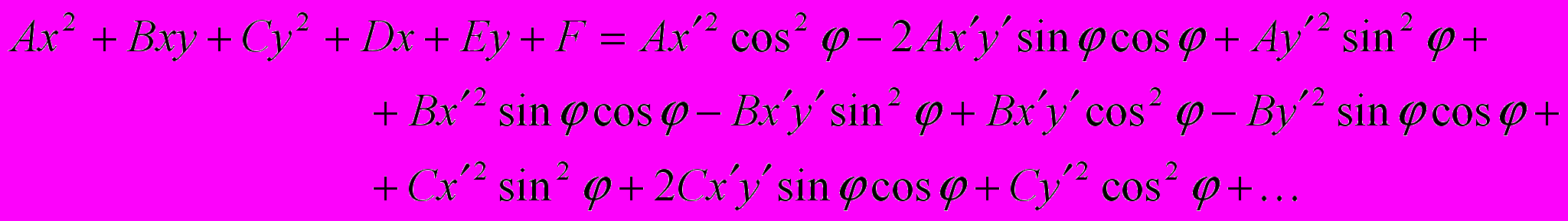
Приравняем нулю получившийся коэффициент перед x′y′:


– 2A sin φ cos φ – Bsin²φ + Bcos²φ + 2Csin φ cos φ = 0.

Или

(C – A) sin 2φ + B cos 2φ = 0.


Если A = C, так как B ≠ 0, то cos 2φ = 0, то есть 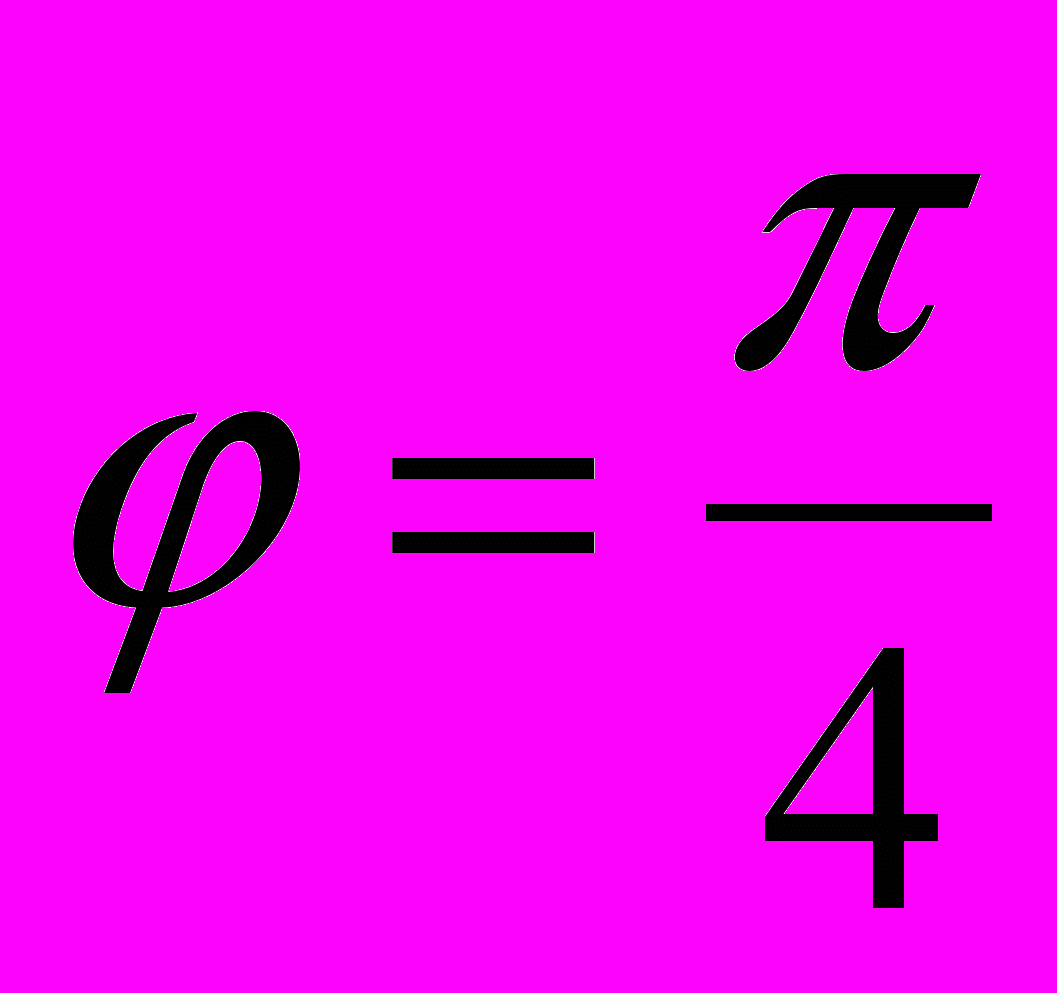. Если же A ≠ C, поделив на cos 2φ, мы получим, что 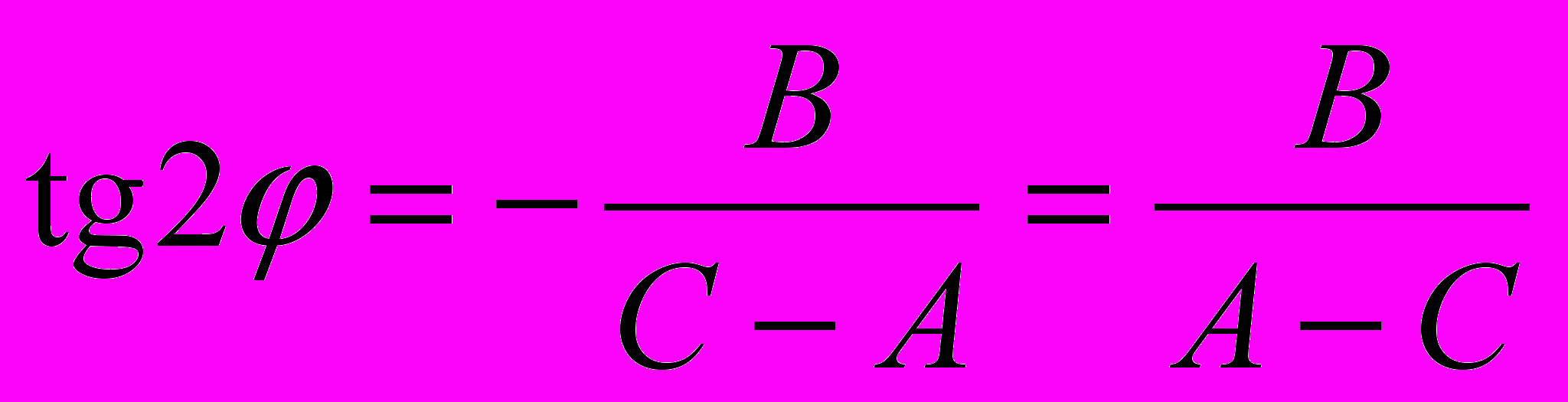, то есть 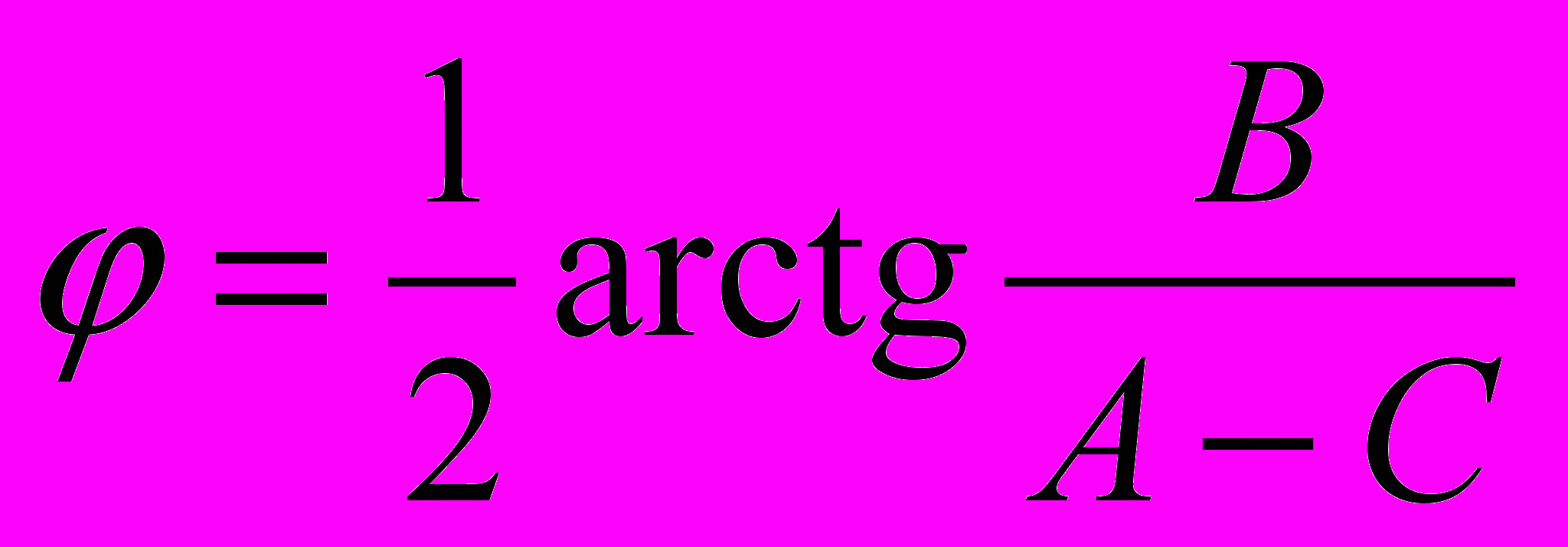. Итак, в новой повернутой системе координат уравнение (1) примет вид


.


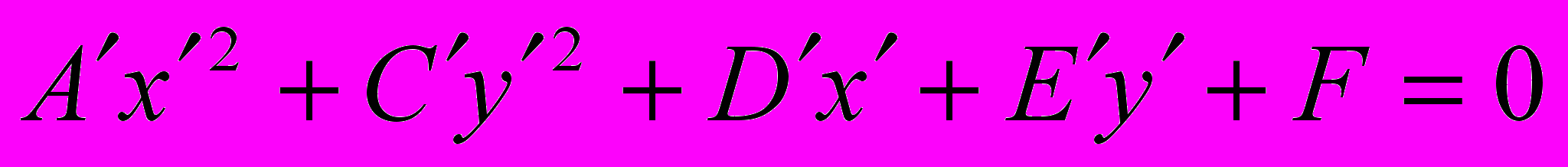Теперь B = 0. Покажем, что переносом начала координат можно избавиться от членов первого порядка Dx и Ey в уравнении (1), которое будет иметь вид


Ax² + Cy² + Dx + Ey + F = 0. (1′)


Если система координат xOy получается из системы координат x′Oy′ переносом на вектор (x₀, y₀), то связь координат в этих системах задается следующими равенствами:


x = x′ + x₀,

y = y′ + y₀,


Перепишем уравнение (1′) в новых координатах:





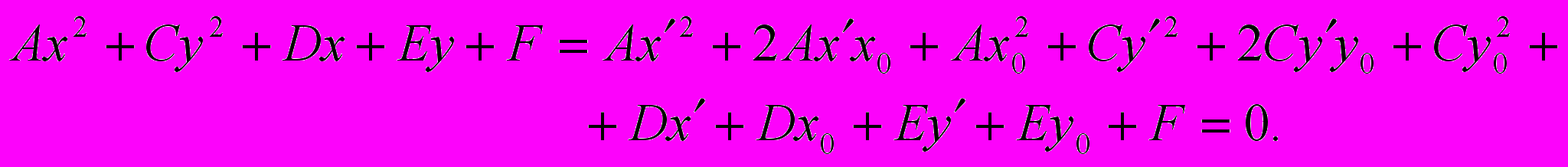
Обозначим через ^ F′ свободный член: 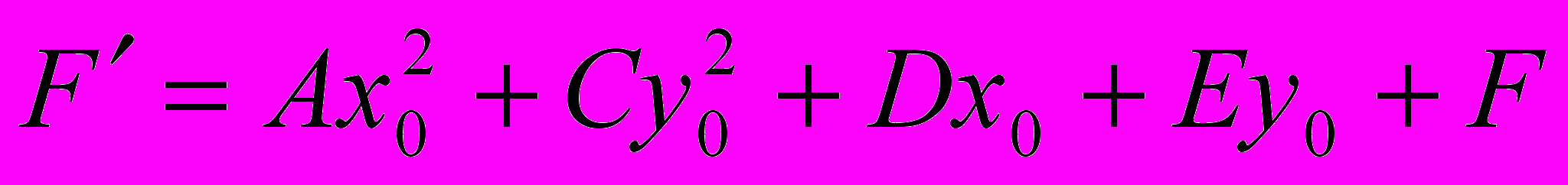. Приравняем нулю коэффициенты при x′ и y′:

2Ax₀ + D = 0,

2Cy₀ + E = 0,


Если A = 0, то D = 0, если C = 0, то E = 0, и уравнение (1′) не содержит членов первого порядка. Поэтому предположим, что A ≠ 0 и C ≠ 0. Тогда для координат вектора (x₀, y₀) мы получим следующие выражения:




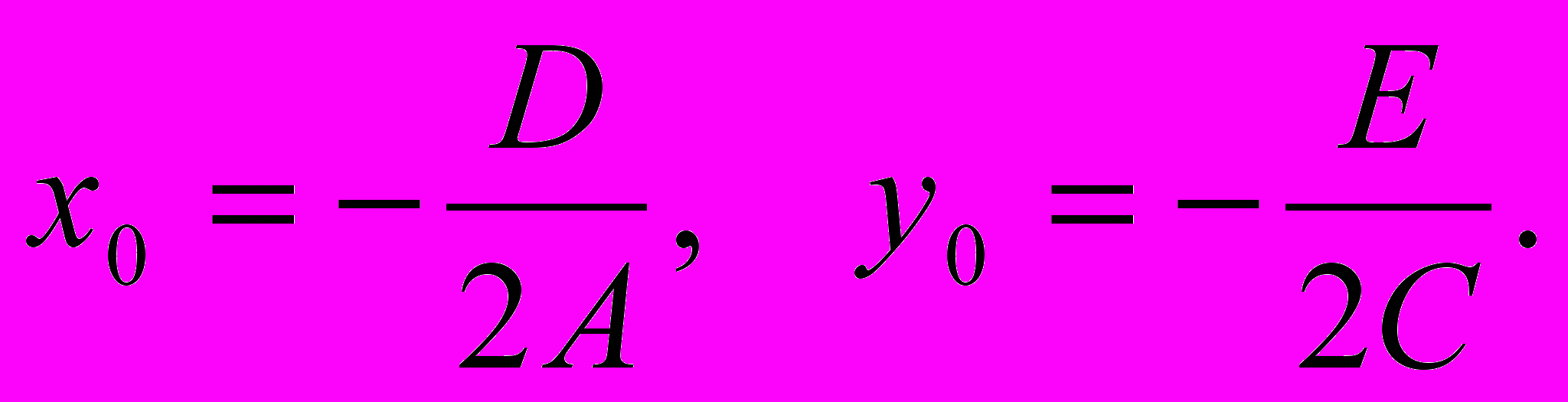
В новых координатах уравнение (1′) примет вид


.


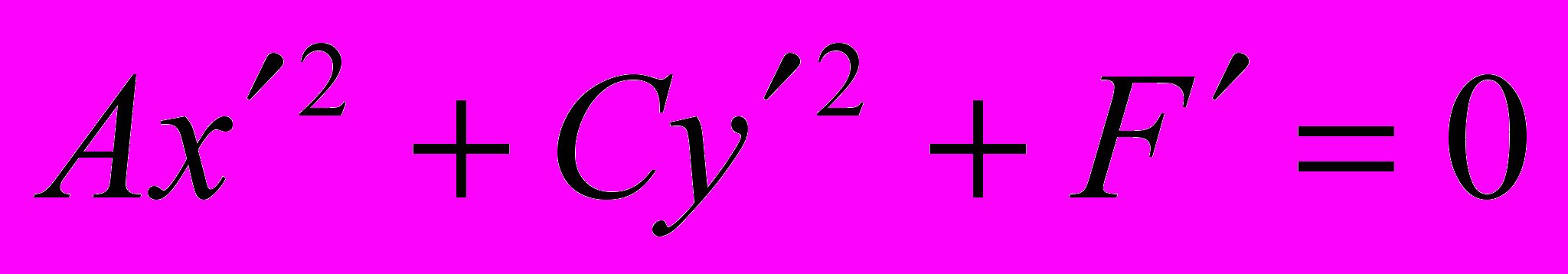Мы показали, что всегда найдется такая система координат, в которой уравнение (1) линии второго порядка будет иметь вид

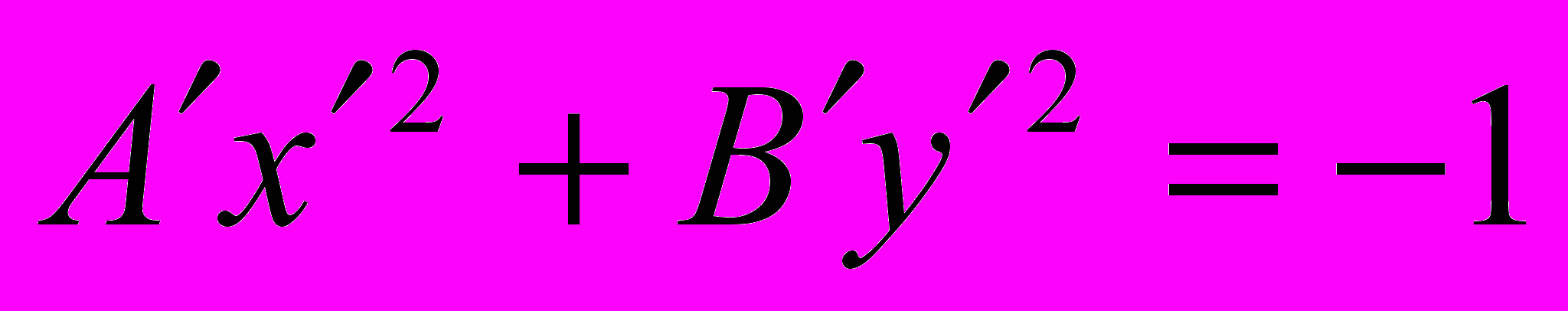, если F′ ≠ 0,

или 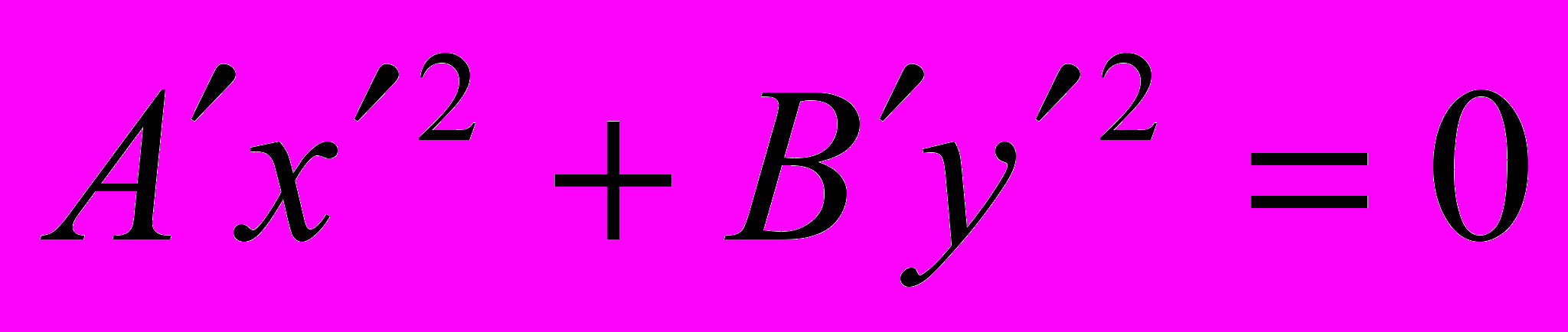, если F′ = 0.

Теорема 2. Пусть в декартовой прямоугольной системе координат линия задается уравнением (1). Тогда существует система координат, в которой уравнение (1) линии второго порядка принимает один из следующих девяти канонических видов:


1. 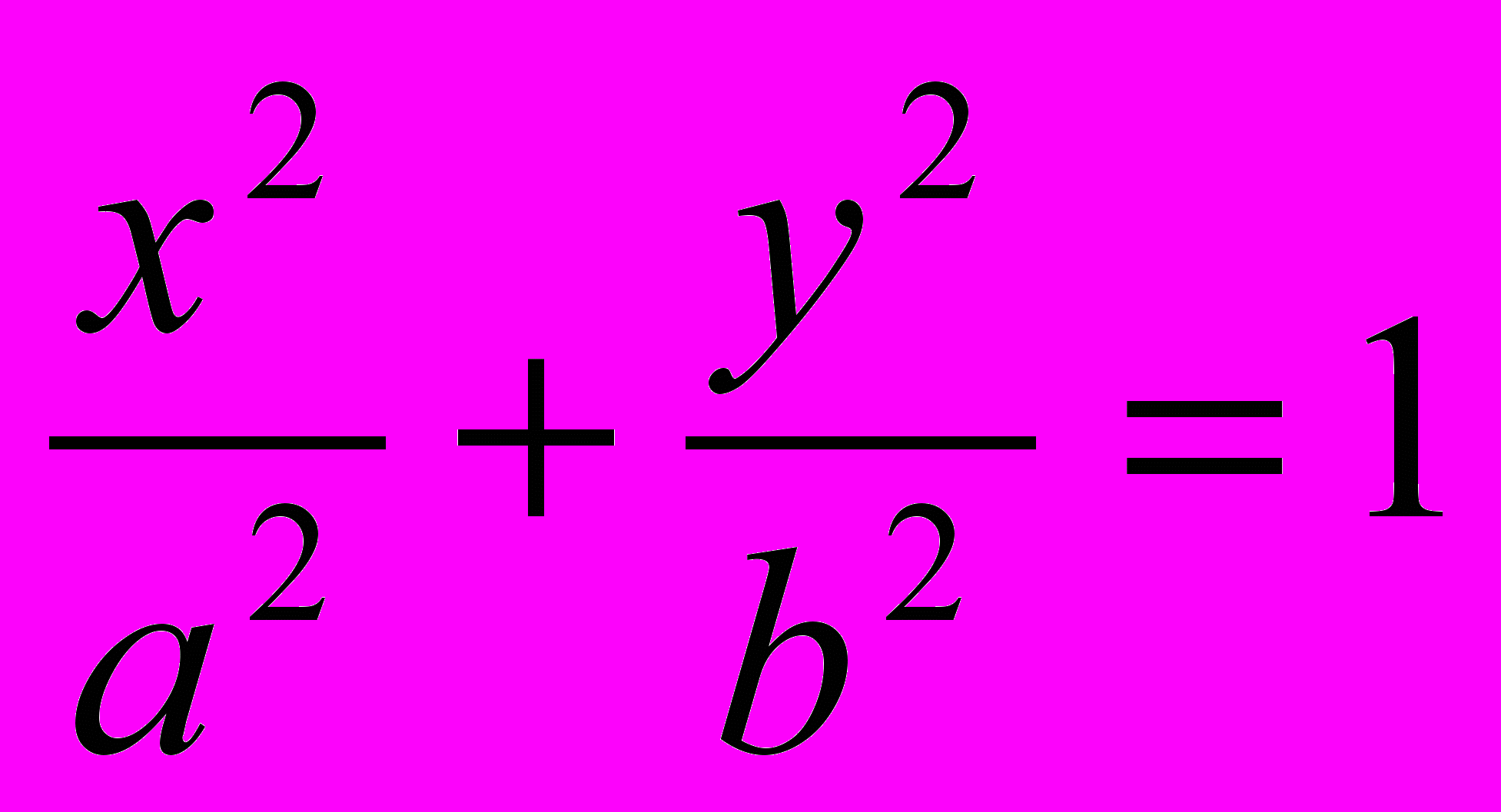– уравнение эллипса;


2. 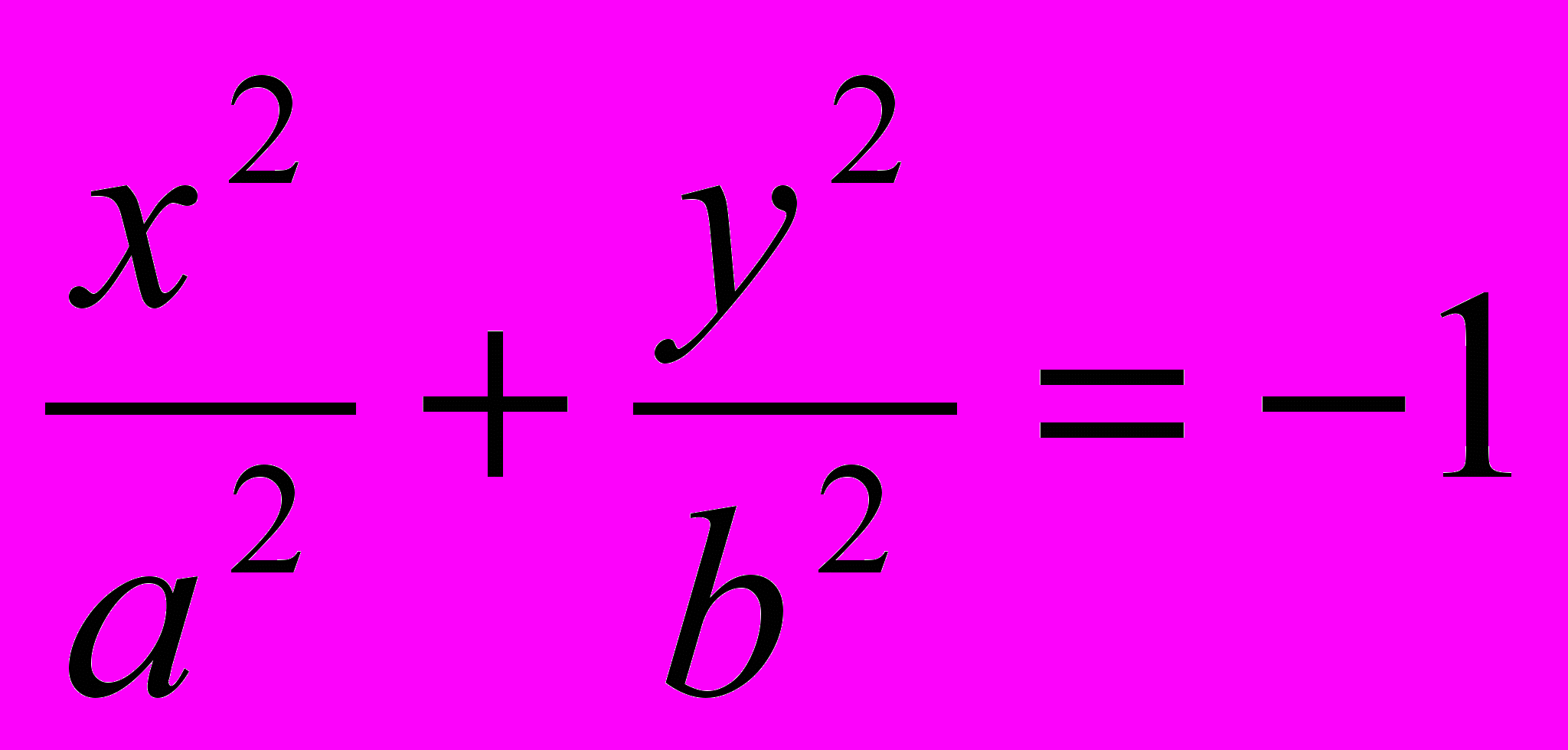– уравнение мнимого эллипса;


3. 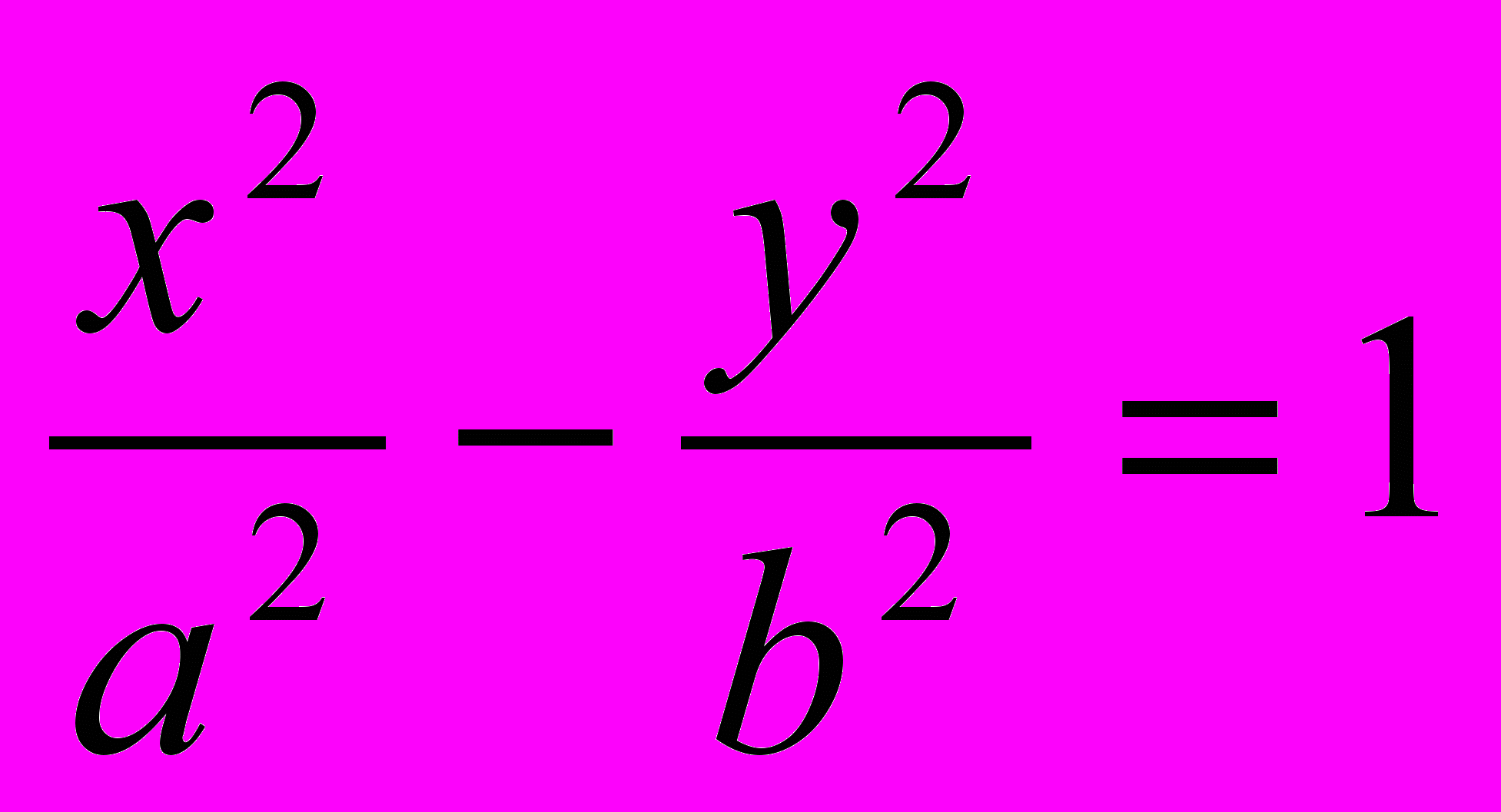– уравнение гиперболы;


4. y² = 2px – уравнение параболы;


5. 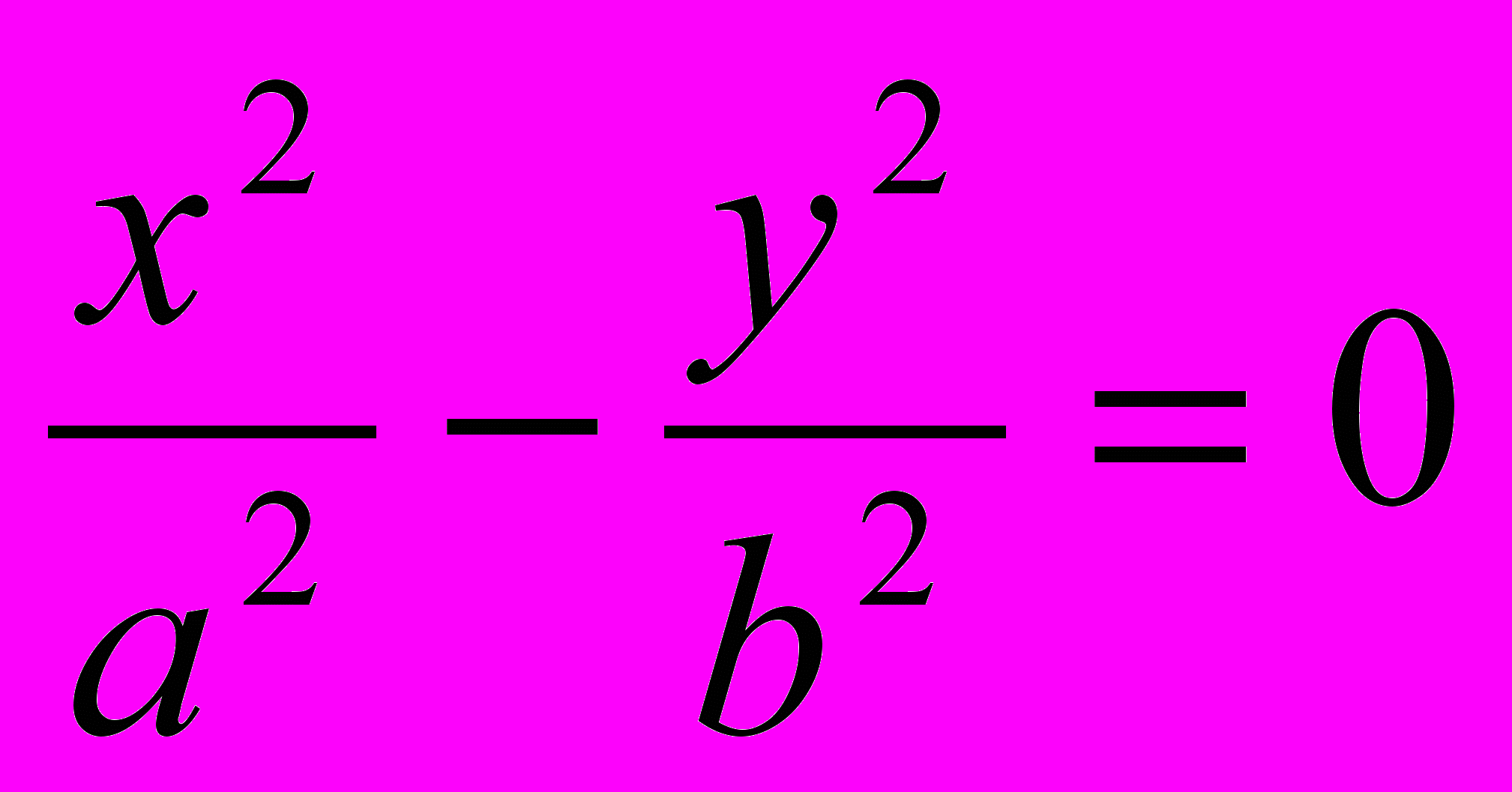– уравнение пары пересекающихся прямых;


6. 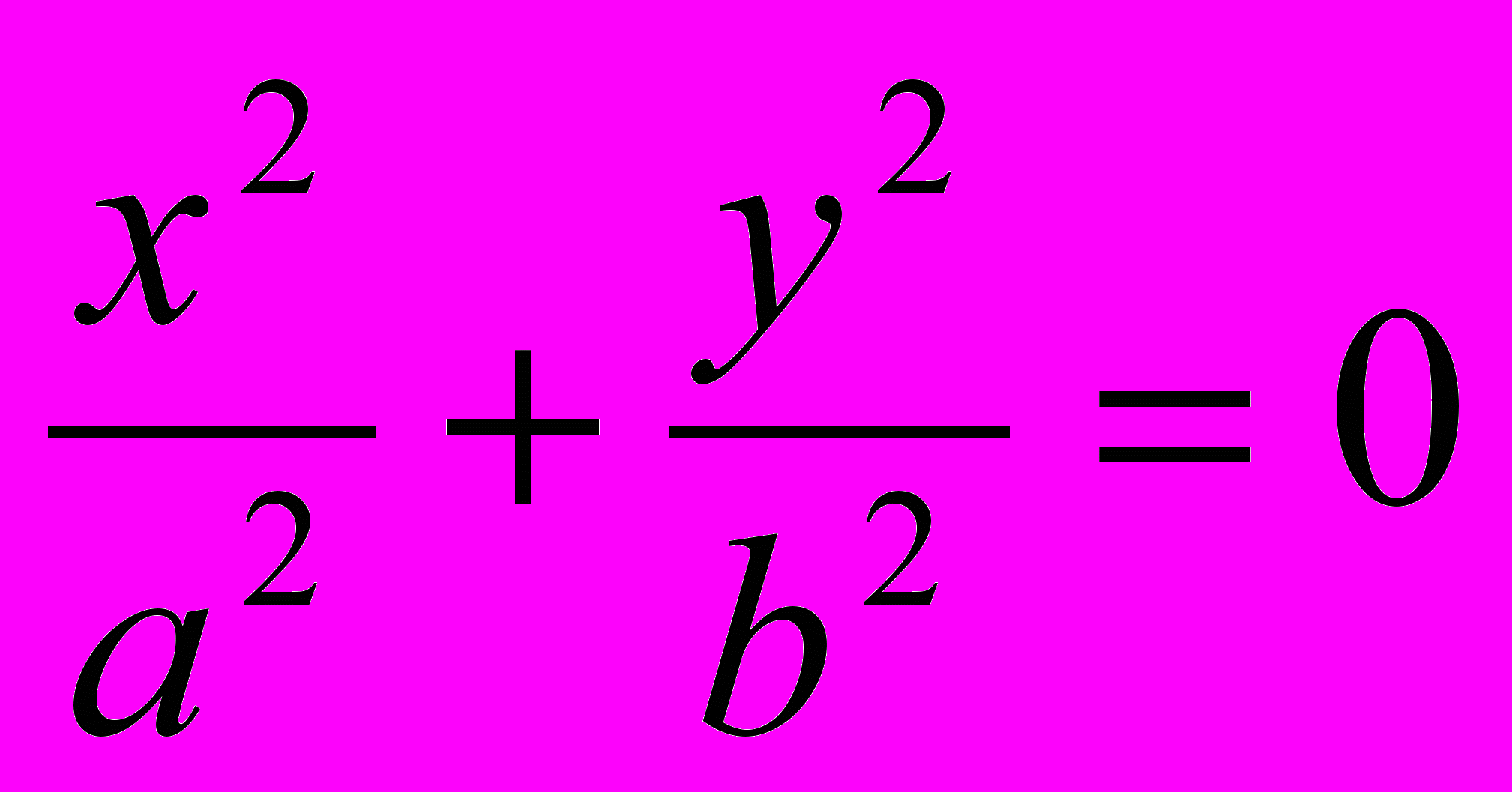– уравнение пары мнимых пересекающихся прямых;


7. y² – b² = 0 – уравнение пары параллельных прямых;


8. y² + b² = 0 – уравнение пары мнимых параллельных прямых;


9. y² = 0 – уравнение пары совпадающих прямых.