Рабочая программа учебной дисциплины ен. Ф. 01. Аналитическая геометрия и линейная алгебра

Вид материала

Рабочая программа

Содержание 1. Пояснительная записка 1.2 Цели и задачи дисциплины. 2. Структура учебной дисциплины. 3. Содержание учебной дисциплины 3.2 Содержание практических занятий 4. Методические материалы и рекомендации для преподавателя 4.2. Примерные задания итоговой контрольной работы. 5. Перечень форм и методов самостоятельной работы 6. Формы текущего, промежуточного и итогового контроля. 7. Список литературы

Подобный материал:

• Рабочая программа учебной дисциплины линейная алгебра и аналитическая геометрия уровень, 426.51kb.
• Учебно-методический комплекс учебной дисциплины ен. Ф. 01 Математика (аналитическая, 542.76kb.
• Рабочая программа дисциплины (модуля) «Линейная алгебра и аналитическая геометрия», 275.82kb.
• Рабочая программа учебной дисциплины «Алгебра и геометрия» Направление подготовки, 137.66kb.
• Лекции, час, 202.55kb.
• Линейная алгебра и аналитическая геометрия, 103.33kb.
• Рабочая учебная программа дисциплины (модуля) Линейная алгебра, 227.98kb.
• Рабочая учебная программа дисциплины (модуля) Алгебра и геометрия, 207.66kb.
• Рабочая программа «Механика и основы механики сплошных сред» Специальность 010400 физика,, 141.09kb.
• Программа дисциплины линейная алгебра и аналитическая геометрия по специальности 553100, 119.01kb.

Министерство образования и науки Российской Федерации

Федеральное агентство по образованию

Псковский государственный педагогический университет

имени С.М. Кирова

Физико-математический факультет

Кафедра алгебры и геометрии

«Утверждаю»

Декан физико-математического факультета

_______________И.Н. Медведева

«_____»_____________200__г.

РАБОЧАЯ ПРОГРАММА

учебной дисциплины

ЕН.Ф.01. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ

И ЛИНЕЙНАЯ АЛГЕБРА


ООП: Специальность 030600.00 Технология и предпринимательство

(код ОКСО 050502)

Факультет: технологии и предпринимательства

Форма обучения: дневная

I курс, 1 семестр

Всего часов: 60

Лекции: 20

Практические работы: 16

Лабораторные работы: 0

Самостоятельная работа: 24

Зачет: 1 семестр


Псков

2007

Рабочая программа составлена на основании Государственного образовательного стандарта высшего профессионального образования по специальности 030600.00 Технология и предпринимательство.


Номер государственной регистрации

№ 663 пед/сп (новый)

«31» января 2005 г.


Рабочая программа принята на заседании кафедры алгебры и геометрии.


Протокол № ____ заседания кафедры

«____»____________ 200 __ г.


Программу разработал доцент кафедры алгебры и геометрии, кандидат физико-математических наук


__________________________ А.Н. Зуев


Заведующий кафедрой алгебры и геометрии

________________________ И.Н. Медведева


1. Пояснительная записка

1.1 Требования к содержанию учебной дисциплины из Государственного образовательного стандарта.

ЕН.Ф.01

Математика Аналитическая геометрия и линейная алгебра; дифференциальное, интегральное исчисления, гармонический анализ; дифференциальные уравнения; численные методы; функции комплексного переменного; элементы функционального анализа; вероятность и статистика: теория вероятностей, случайные процессы, статистическое оценивание и проверка гипотез, статистические методы обработки экспериментальных данных.

334

1.2 Цели и задачи дисциплины.

Курс линейной алгебры и аналитической геометрии в педагогическом университете имеет своей целью изложить основы этой науки и создать фундамент математического образования студента-технолога. Работа над курсом предоставляет студентам необходимые знания и достаточную практическую подготовку для последующего изучения целого ряда специальных и общих дисциплин. В тоже время предлагаемый курс является вполне естественным обобщением основного содержания школьных курсов математики.

Подготовка выпускника факультета вызывает необходимость ускоренного прохождения курса математики без потери глубины изложения. В связи с этим упор в изложении делается на наиболее общие вопросы.

Основой учебных занятий являются лекции, которые призваны задавать достаточно высокий научный уровень. Лекции подкрепляются практическими занятиями, на которых знания и представления, полученные на лекциях, доводятся до уровня умений и навыков.

Большое значение отводится индивидуальной работе со студентами. Она проводится в часы самостоятельной работы в форме консультаций. Текущий контроль результатов освоения курса проводится на практических занятиях. В качестве контрольных мероприятий плвнируются контрольная работа, защита типового расчета и зачет.

В первой теме рассматриваются операции над множествами и матрицами. Даются правила вычисления определителей второго и третьего порядков, свойства определителей. Выводятся формулы Крамера. Системы третьего порядка решаются также матричным способом и методом Гаусса.

Вторая глава посвящена векторной алгебре. Вводятся понятия коллинерности, компланарности векторов, линейной зависимости векторов, базиса, доказываются теоремы о проекциях. Даны определения, свойства и приложения скалярного, векторного и смешанного произведения векторов.

В третьей теме рассматриваются общее и каноническое уравнения прямой на плоскости, уравнение в отрезках на осях, угловой коэффициент, уравнение прямой, проходящей через две точки, угол между прямыми, расстояние от точки до прямой, пучок прямых, общий вид кривой второго порядка, окружность, эллипс, гипербола и парабола.

В четвертой теме даются векторное уравнение плоскости, общее уравнение, связка плоскостей, уравнение в отрезках на осях, угол между плоскостями, уравнение плоскости, проходящей через три точки, расстояние от точки до плоскости. Рассматриваются общее, векторное, параметрическое и каноническое уравнения прямой, уравнение прямой, проходящей через две точки, угол между прямыми, условие компланарности двух прямых, угол между прямой и плоскостью, точка их пересечения, пучок плоскостей. Из поверхностей второго порядка рассмотрены сфера, цилиндрические и конические поверхности, поверхность вращения, эллипсоид, гиперболоиды и параболоиды.

Пятая тема посвящена собственным значениям и собственным векторам матрицы, линейным отображениям и приведению квадратичной формы к каноническому виду с помощью ортогонального преобразования.


2. Структура учебной дисциплины.

Тема	ЛК	ПР	СР
1. Множества. Матрицы. Определители. Системы линейных уравнений.	5	3	5
2. Векторная алгебра.	3	3	5
3. Аналитическая геометрия на плоскости.	4	3	5
4. Аналитическая геометрия в пространстве.	4	3	5
5. Линейные отображения.	4	4	4
Итого	20	16	24

3. Содержание учебной дисциплины

3.1 Содержание лекционного курса

№ лек.	Тема лекции	Содержание лекции	Вид контроля
1	Множества. Матрицы.	Множества, действия над ними. Диаграммы Эйлера-Венна. Матрицы. Операции над матрицами.	зачет
2 3	Определители. Обратная матрица.	Определители, свойства. Формулы Крамера. Обратная матрица.	зачет
3	Системы уравнений.	Решение систем матричным способом и методом Гаусса. Векторы и действия над ними. Линейная зависимость. Базис.	зачет
4	Скалярное, векторное и смешанное произведения векторов	Скалярное произведение. Свойства, приложения. Векторное произведение. Свойства, приложения. Смешанное произведение. Свойства, приложения.	зачет
5	Прямая на плоскости	Прямая на плоскости.	зачет
6	Кривые второго порядка	Кривые второго порядка	зачет
7	Аналитическая геометрия в пространстве	Плоскость и прямая в пространстве.	зачет
8	Аналитическая геометрия в пространстве	Поверхности второго порядка.	зачет
9	Линейные отображения	Собственные значения и собственные вектора матрицы. Линейные отображения.
10	Квадратичные формы	Приведение квадратичной формы к каноническому виду с помощью ортогонального преобразования.	зачет

3.2 Содержание практических занятий

№ занят.	Тема практического занятия	Содержание практического занятия	Вид контроля
1	Матрицы. Определители.	Матрицы. Операции над матрицами. Определители, свойства. Формулы Крамера. Обратная матрица.	Самостоят. работа
2	Системы. Вектора.	Решение систем матричным способом и методом Гаусса. Векторы и действия над ними. Линейная зависимость. Базис.	Самостоят. работа
3	Действия с векторами	Скалярное произведение. Свойства, приложения. Векторное произведение. Свойства. Приложения. Смешанное произведение. Свойства, приложения.	Самостоят. работа. Индивид. задание
4	Аналитическая геометрия на плоскости	Прямая на плоскости. Кривые второго порядка.	Индивид. задание.
5	Аналитическая геометрия в пространстве	Плоскость и прямая в пространстве. Поверхности второго порядка.	Самостоят. работа. Контр. работа
6	Линейные отображения	Собственные значения и собственные вектора матрицы. Линейные отображения.	Самостоят. работа
7	Квадратичные формы	Приведение квадратичной формы к каноническому виду с помощью ортогонального преобразования.	Индивид. задание
8	Итоговая контрольная работа	Итоговая контрольная работа.

4. Методические материалы и рекомендации для преподавателя

4.1. Примерный перечень вопросов к зачету

1. Множества, действия над ними. Диаграммы Эйлера-Венна.

2. Матрицы. Операции над матрицами.

3. Определители, свойства. Формулы Крамера.

4. Обратная матрица.

5. Решение систем матричным способом и методом Гаусса.

6. Векторы и действия над ними. Линейная зависимость. Базис.

7. Скалярное произведение. Свойства, приложения.

8. Векторное произведение. Свойства, приложения.

9. Смешанное произведение. Свойства, приложения.

10. Прямая на плоскости.

11. Кривые второго порядка.

12. Плоскость и прямая в пространстве.

13. Поверхности второго порядка.

14. Собственные значения и собственные вектора матрицы.

15. Линейные отображения.

16. Приведение квадратичной формы к каноническому виду с помощью ортогонального преобразования.


4.2. Примерные задания итоговой контрольной работы.


1. Решить систему уравнений по формулам Крамера:




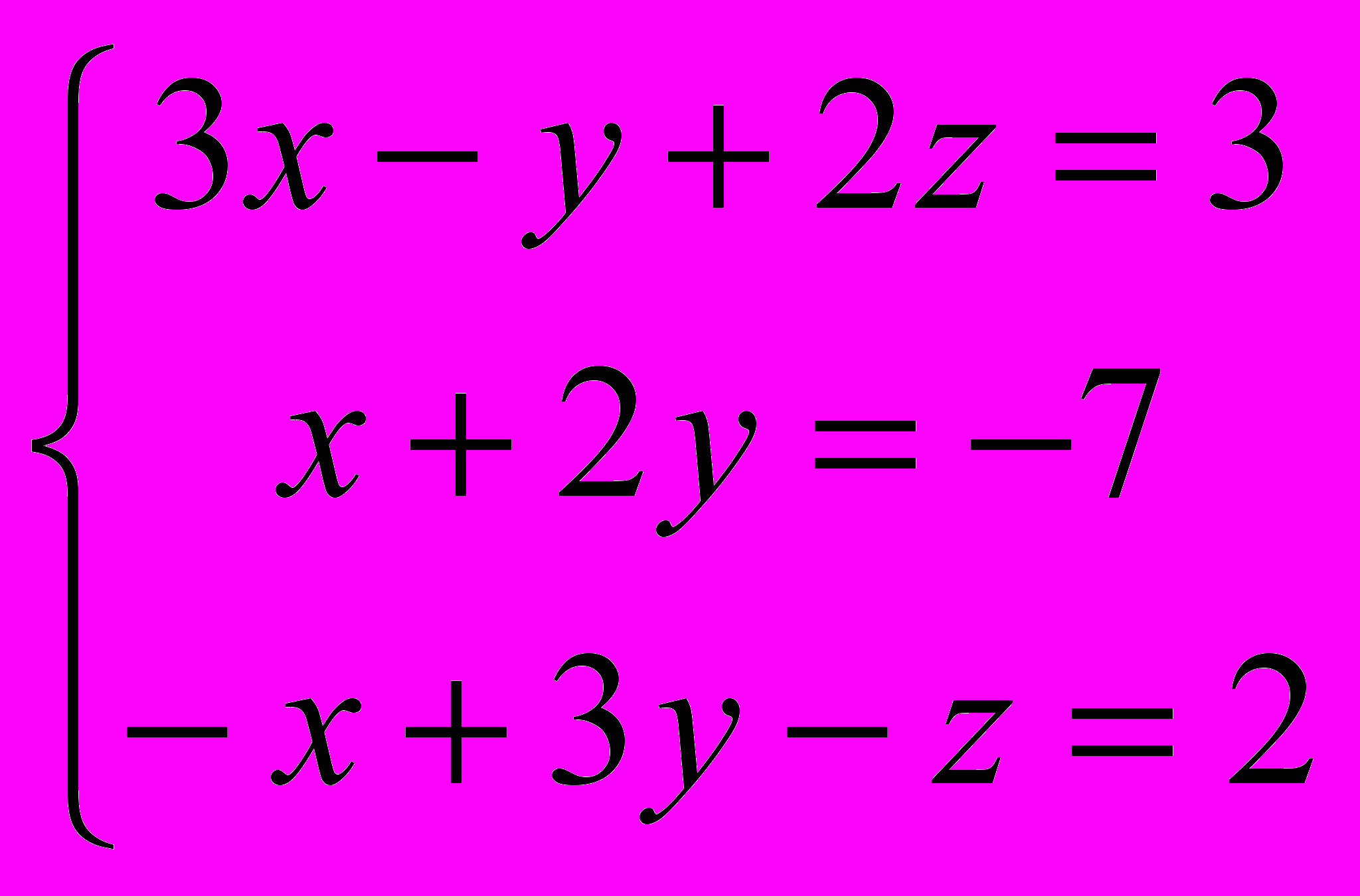
2. Решить систему Аx = В с помощью обратной матрицы:

А= 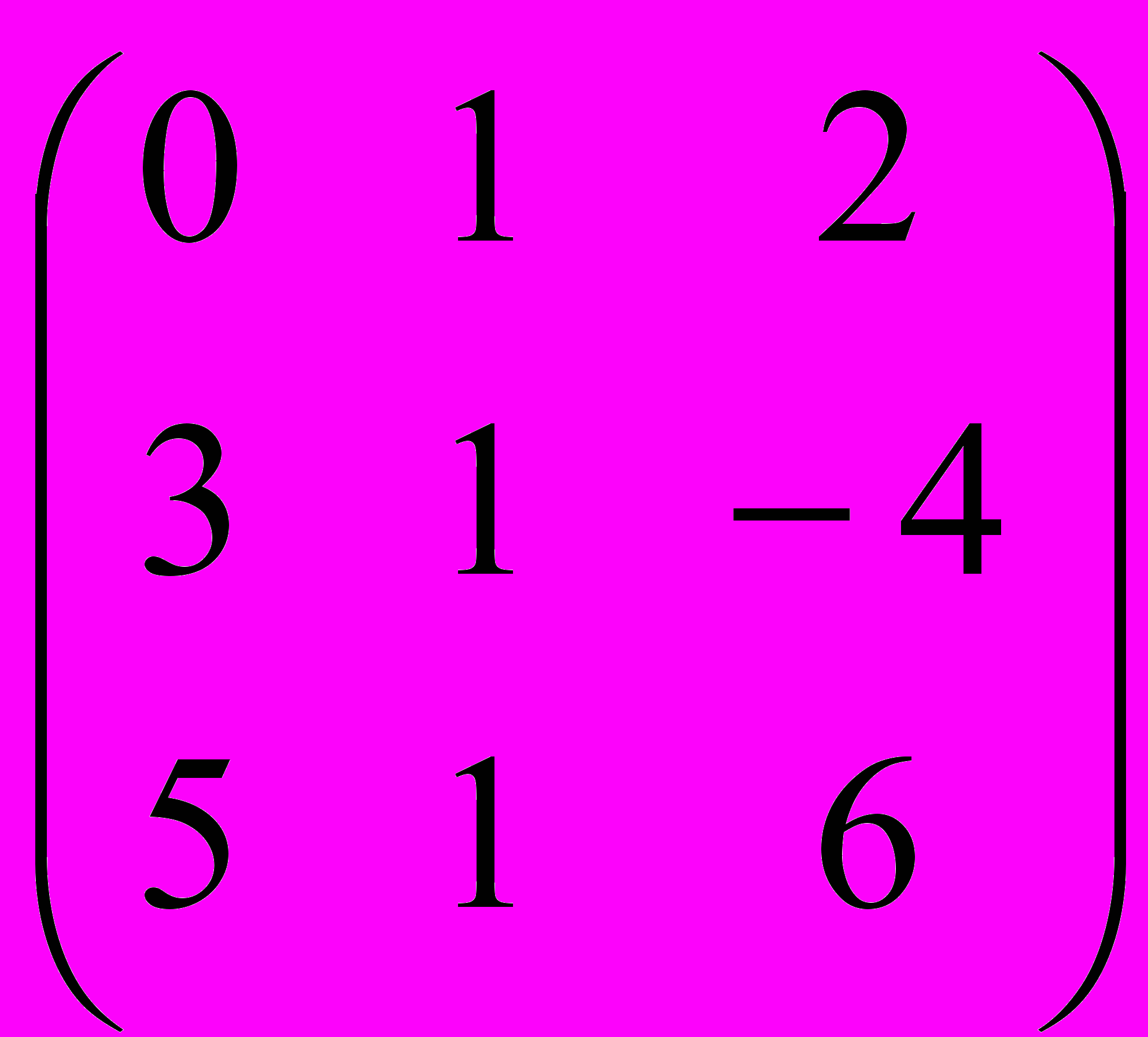В=

3. написать разложение вектора 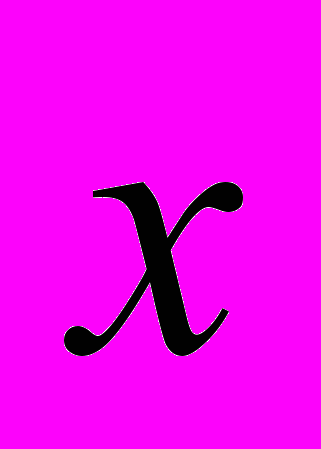по векторам 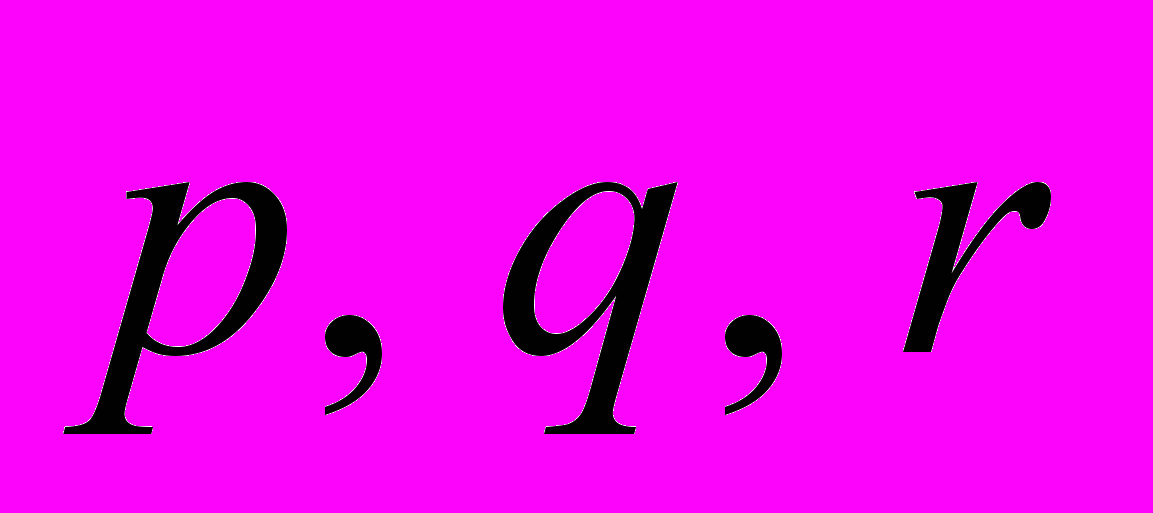, если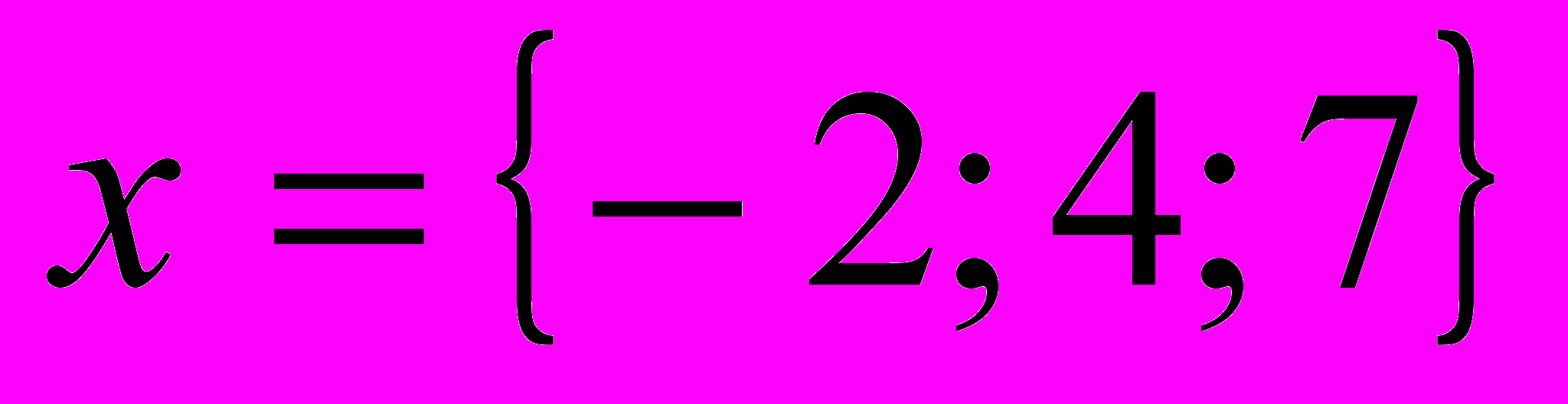



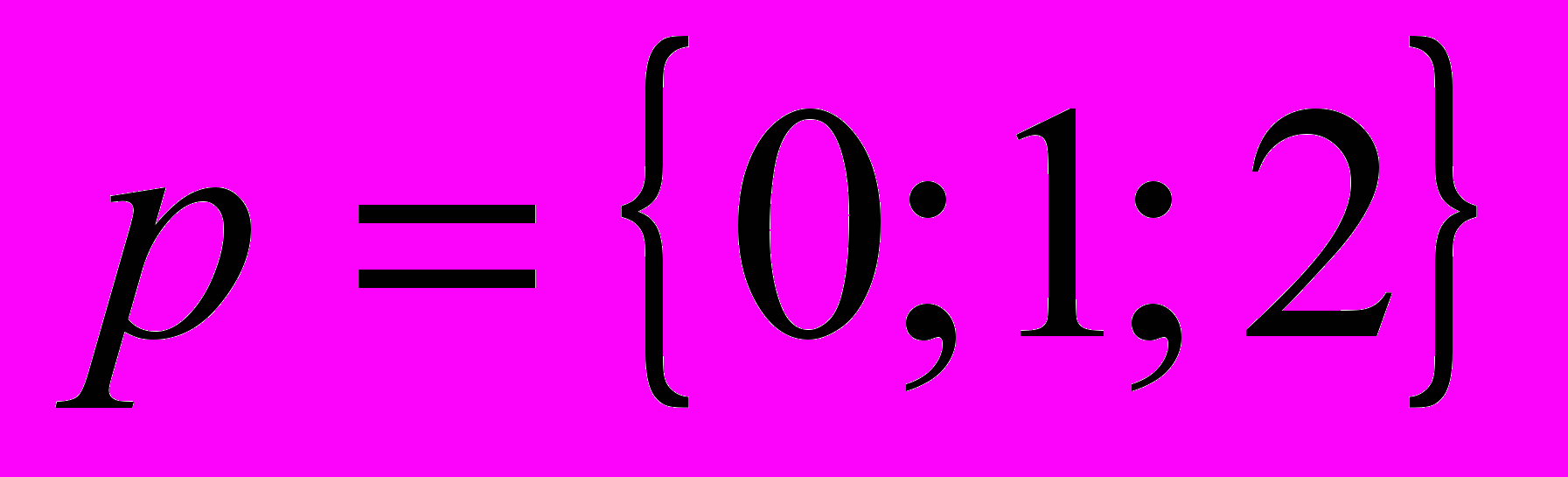
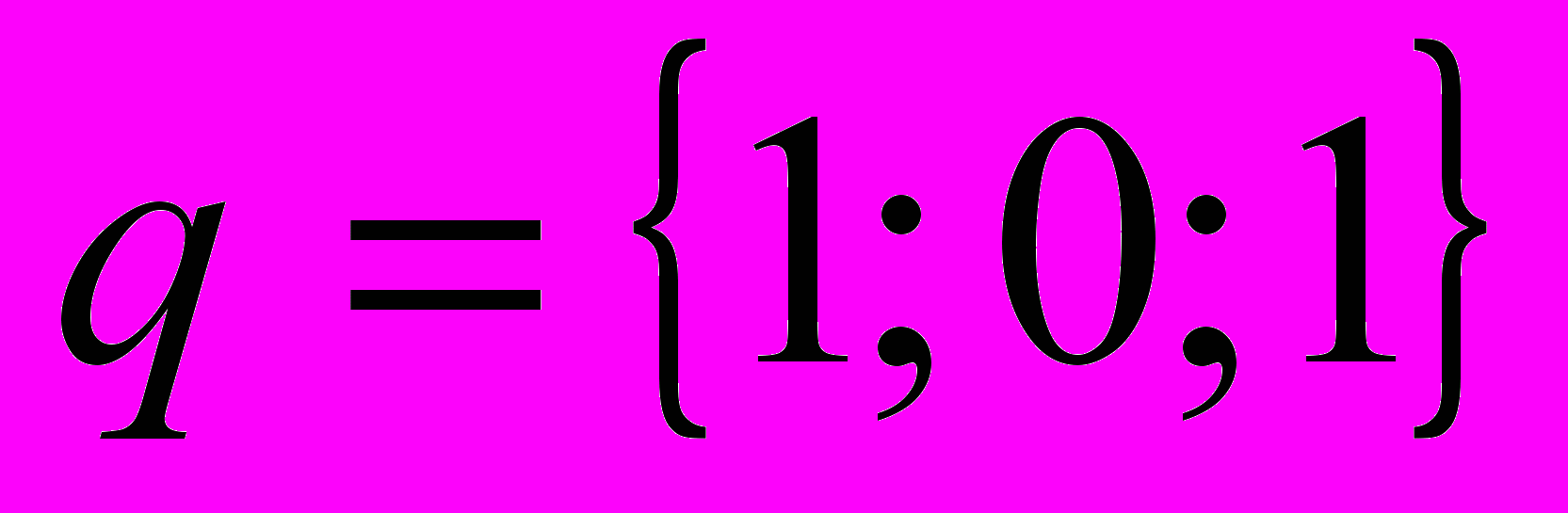
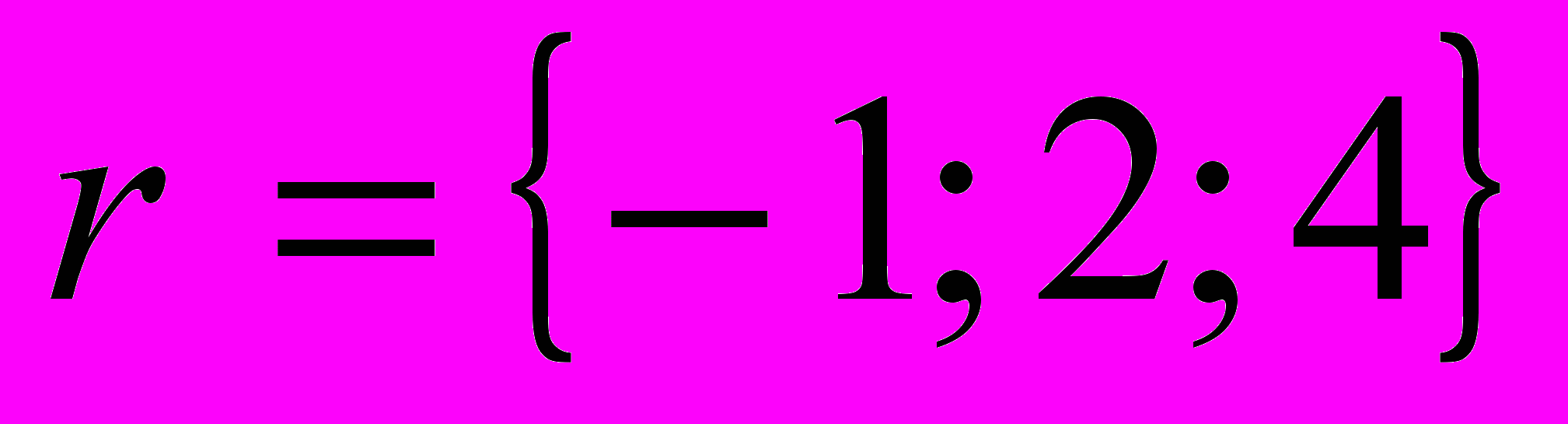
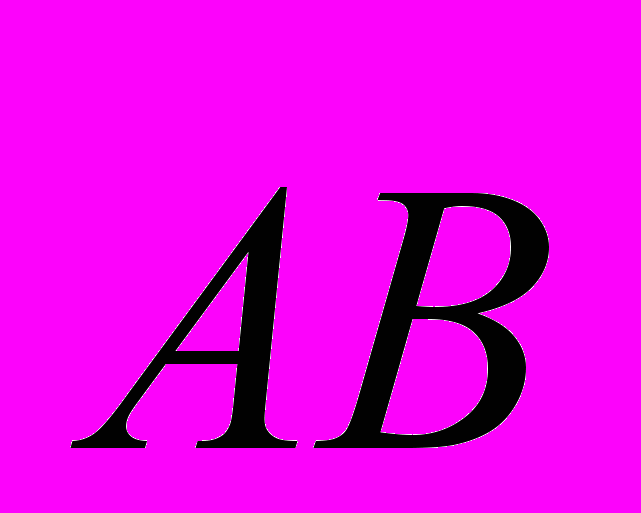
4. Найти косинус угла между векторами и 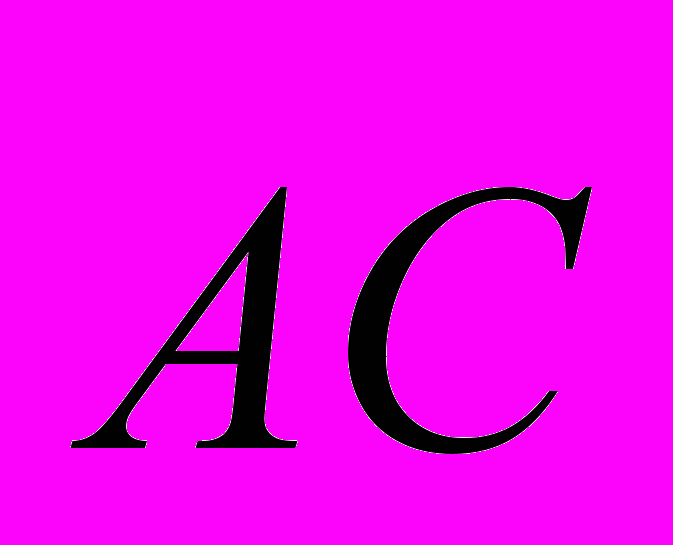, если

А (1; -2; 3), В (0,-1,2) С (3,-4,5)

5. Вычислить площадь параллелограмма, построенного на векторах и ,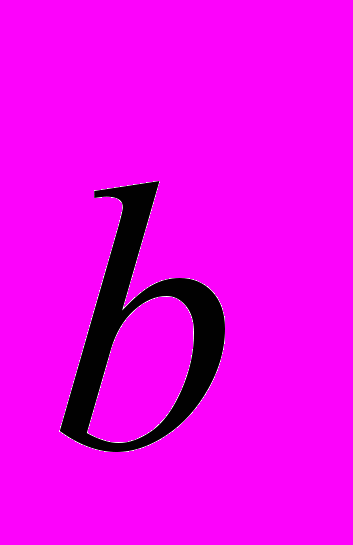

если ; ; .

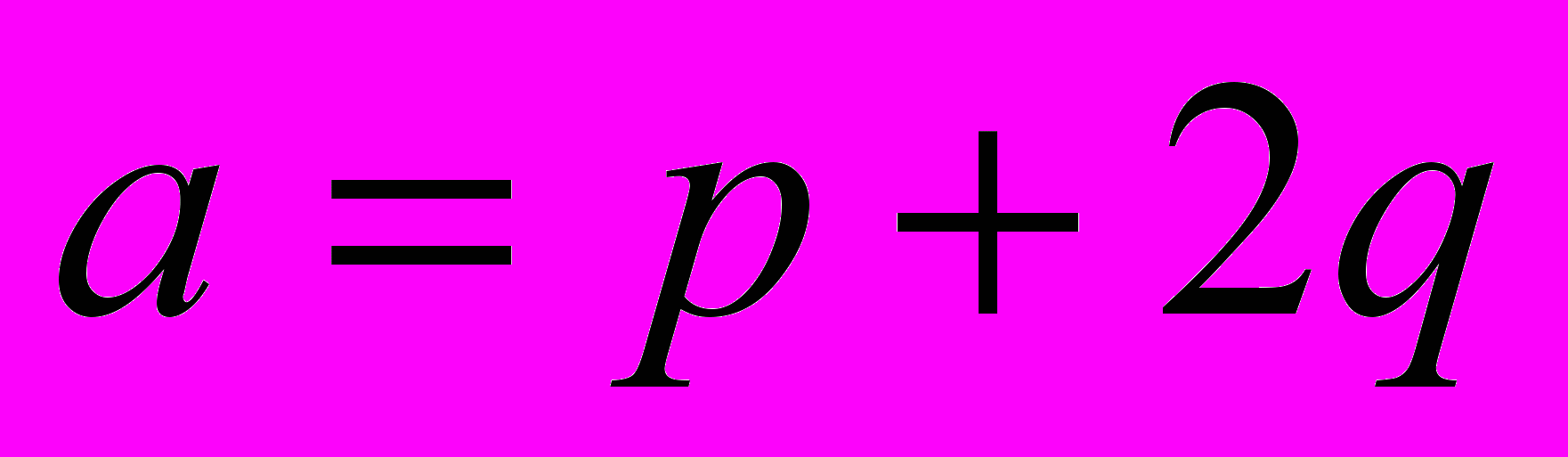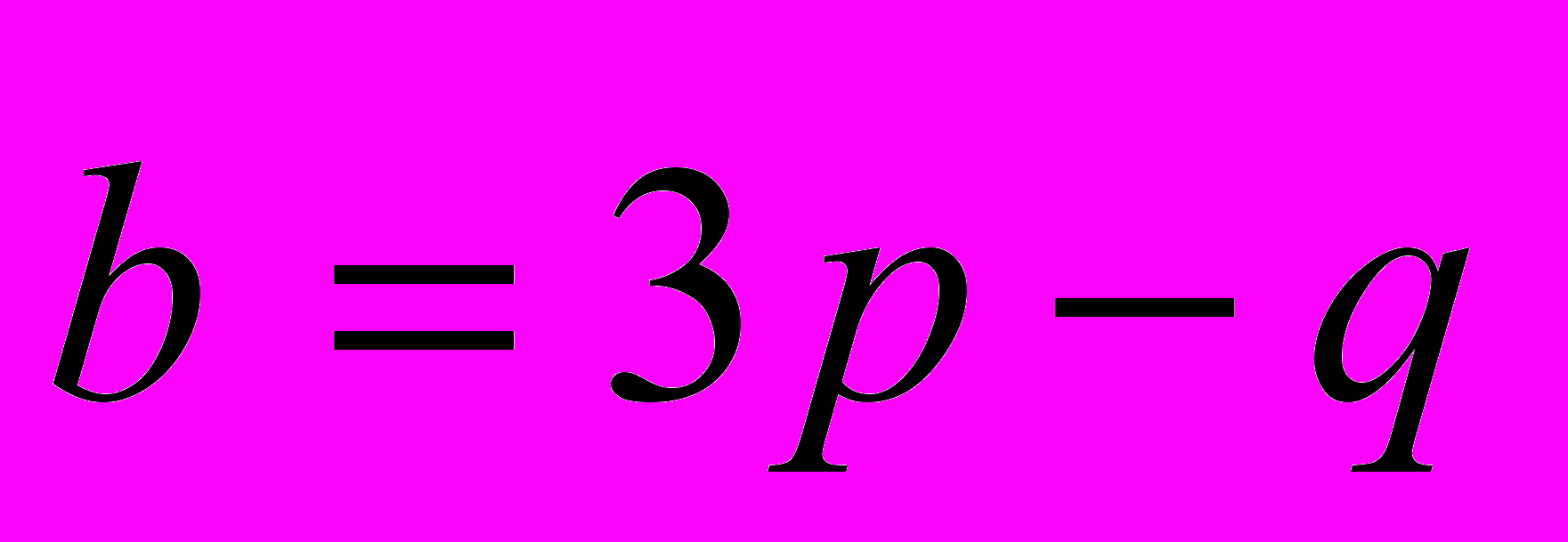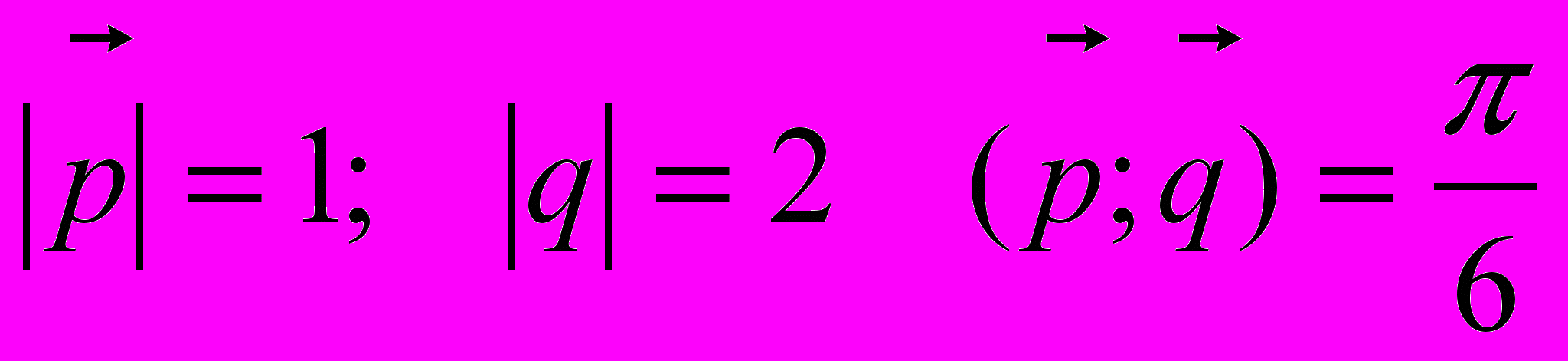6. Вычислить объем тетраэдра с вершинами в точках А₁, А₂, А₃, А₄ и его высоту, опущенную из вершины А₄ на грань А₁А₂А₃ , если

А₁(1;3;6), А₂(2;2;1), А₃(-1;0;1), А₄(-4;6;-3).

7. Найти уравнения высоты, медианы и биссектрисы из вершины А треугольника с вершинами А(3;-1); В(2;4); С(0;-3).

8. Найти точку М₁, симметричную относительно прямой, проходящей через точки А и В, если А(5;-3), В(2;7), М(-2;1).

9. Найти расстояние от точки М_о до плоскости, проходящей через три точки М₁(-3;4;-7), М₂(1;5;-4), М₃(-5;-2;0), М_о(-12;7;-1).

10. Написать каноническое уравнение прямой:

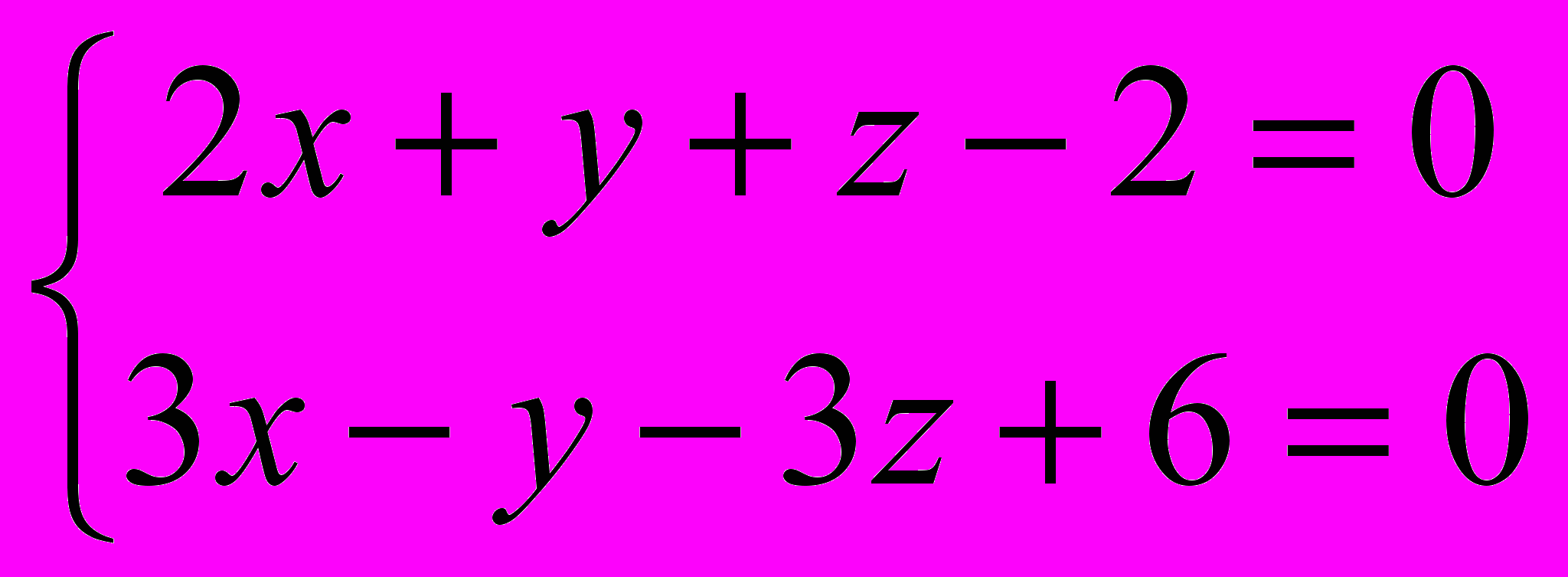
11. Найти точку М₁, симметричную точке М относительно прямой, если М(0;-3;-2); уравнение прямой: .

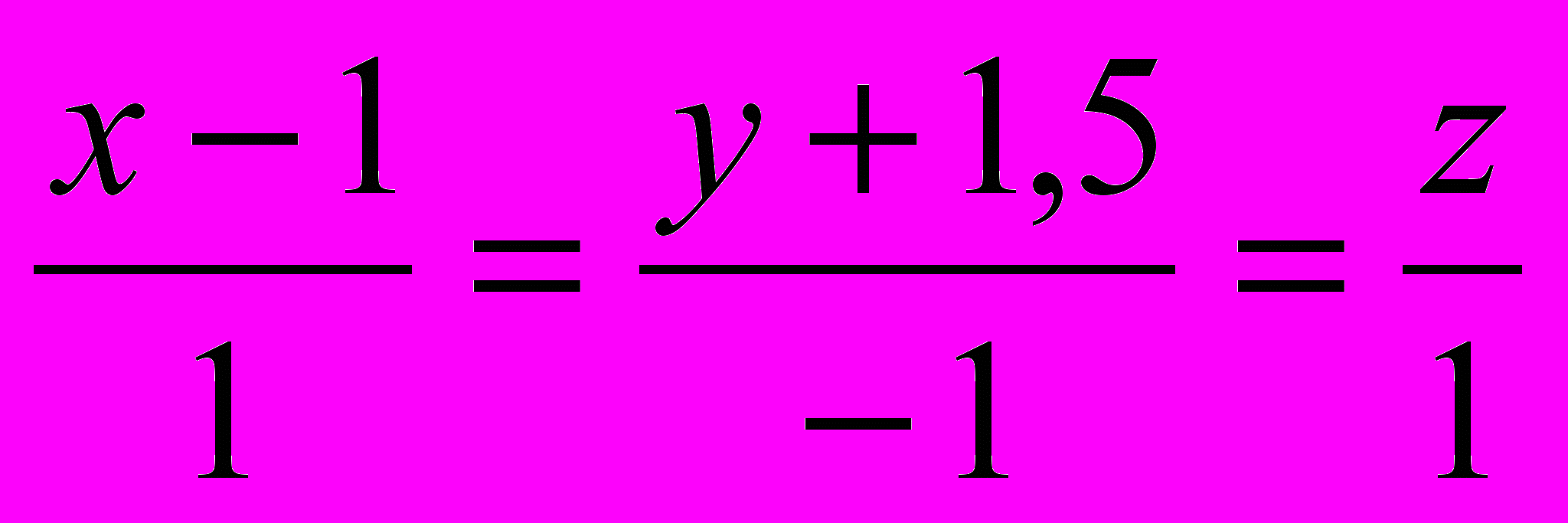12. Найти точку М₁, симметричную точке М относительно плоскости М(1;0;1); 4x+6y+4z-25=0.


13. Найти какой-нибудь базис и определить размерность линейного пространства решений системы:



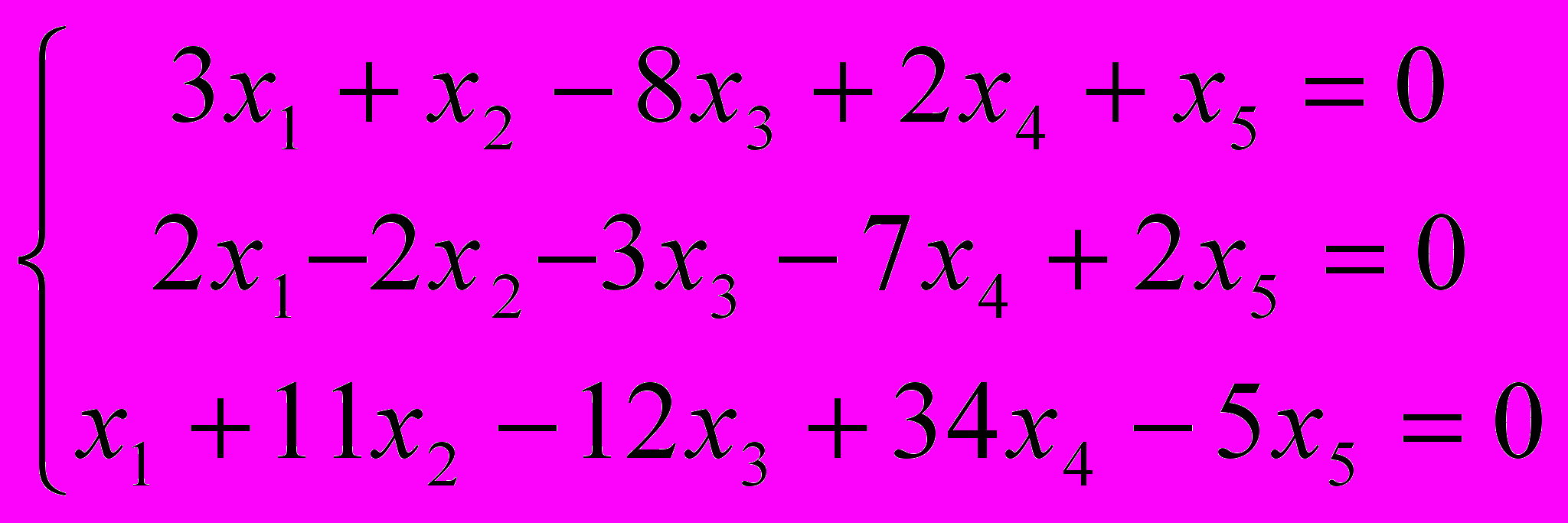
14. Найти координаты вектора 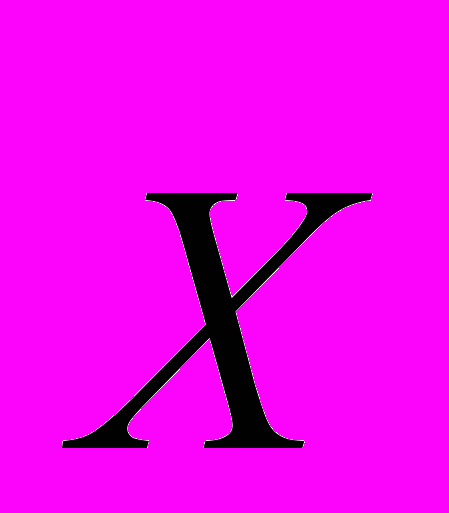в базисе 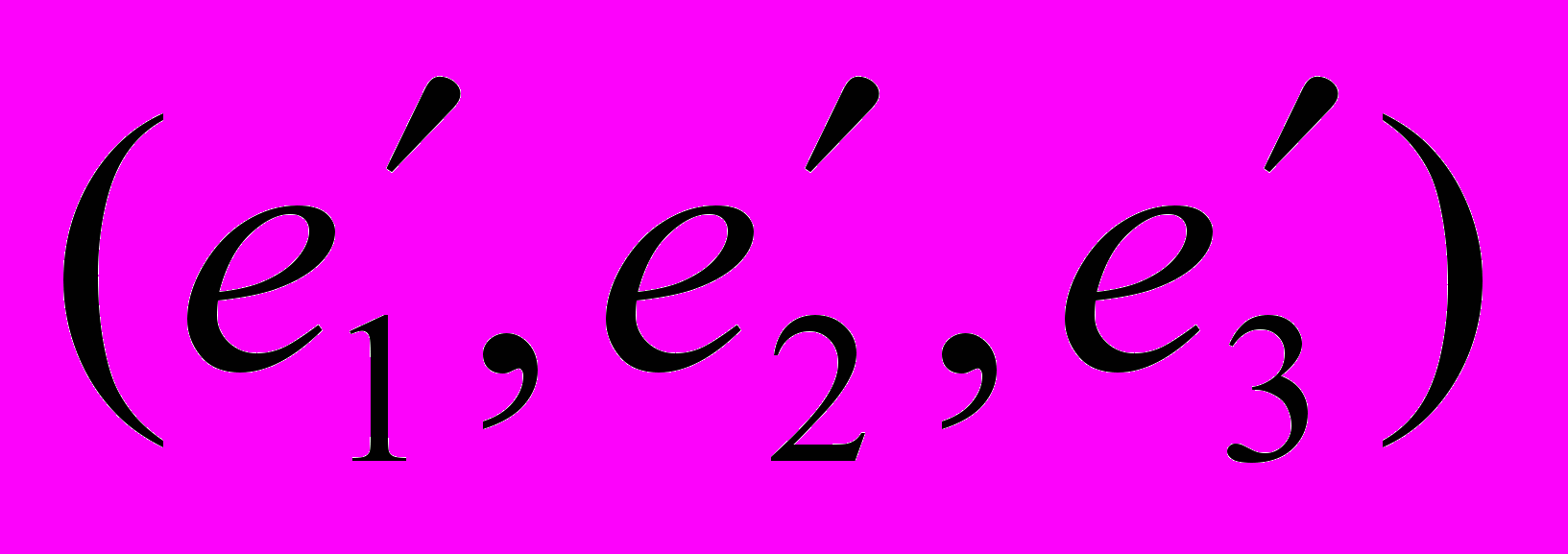, если он задан в базисе : .

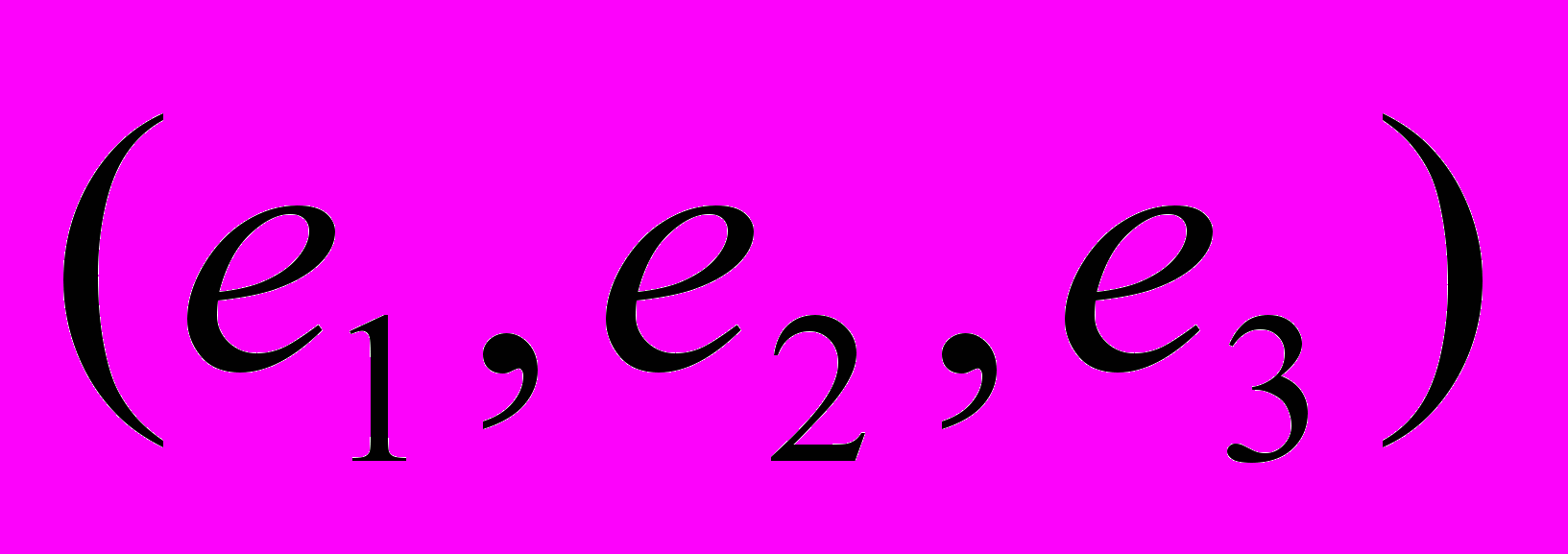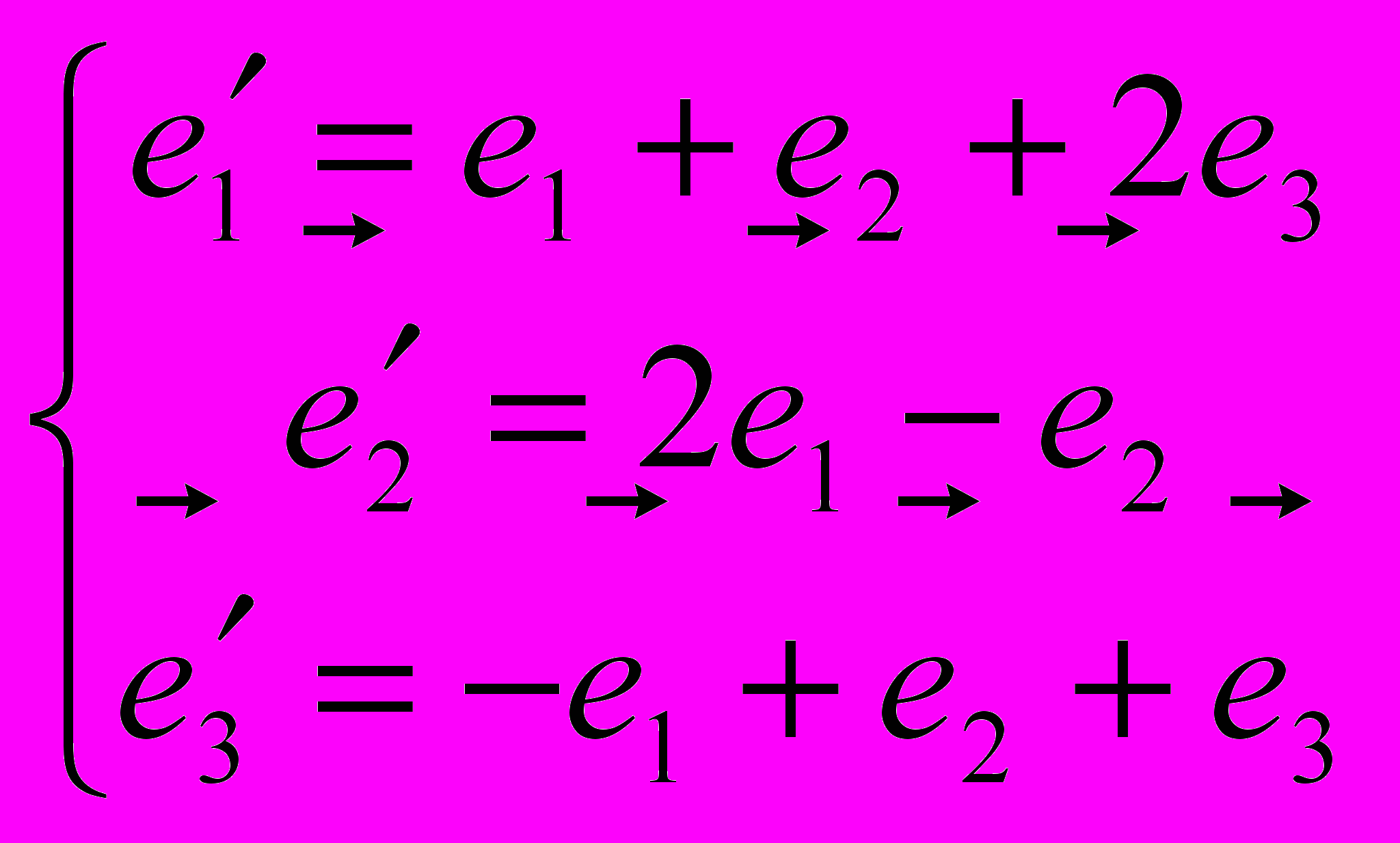
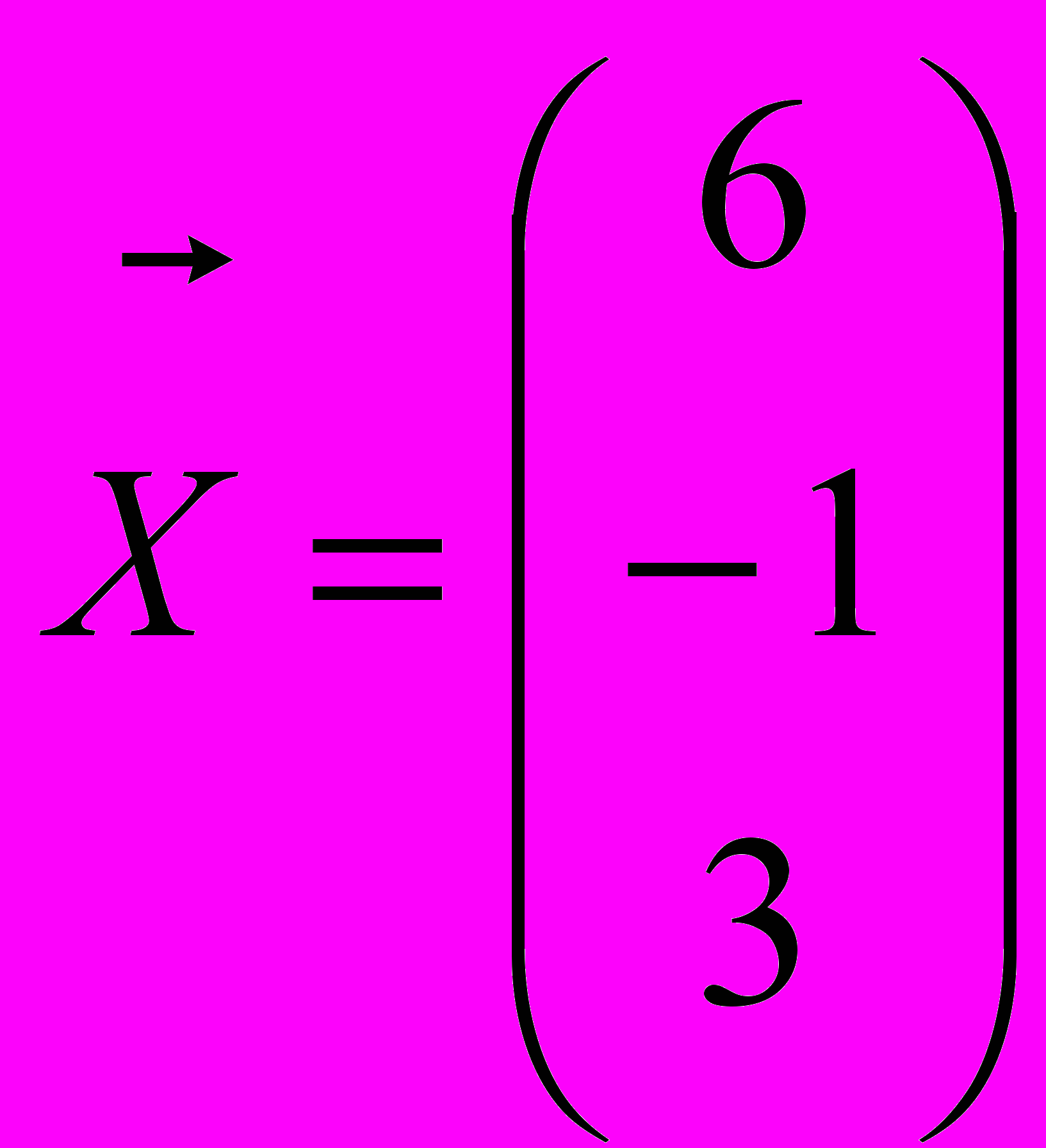15. Найти собственные значения и собственные векторы матрицы .

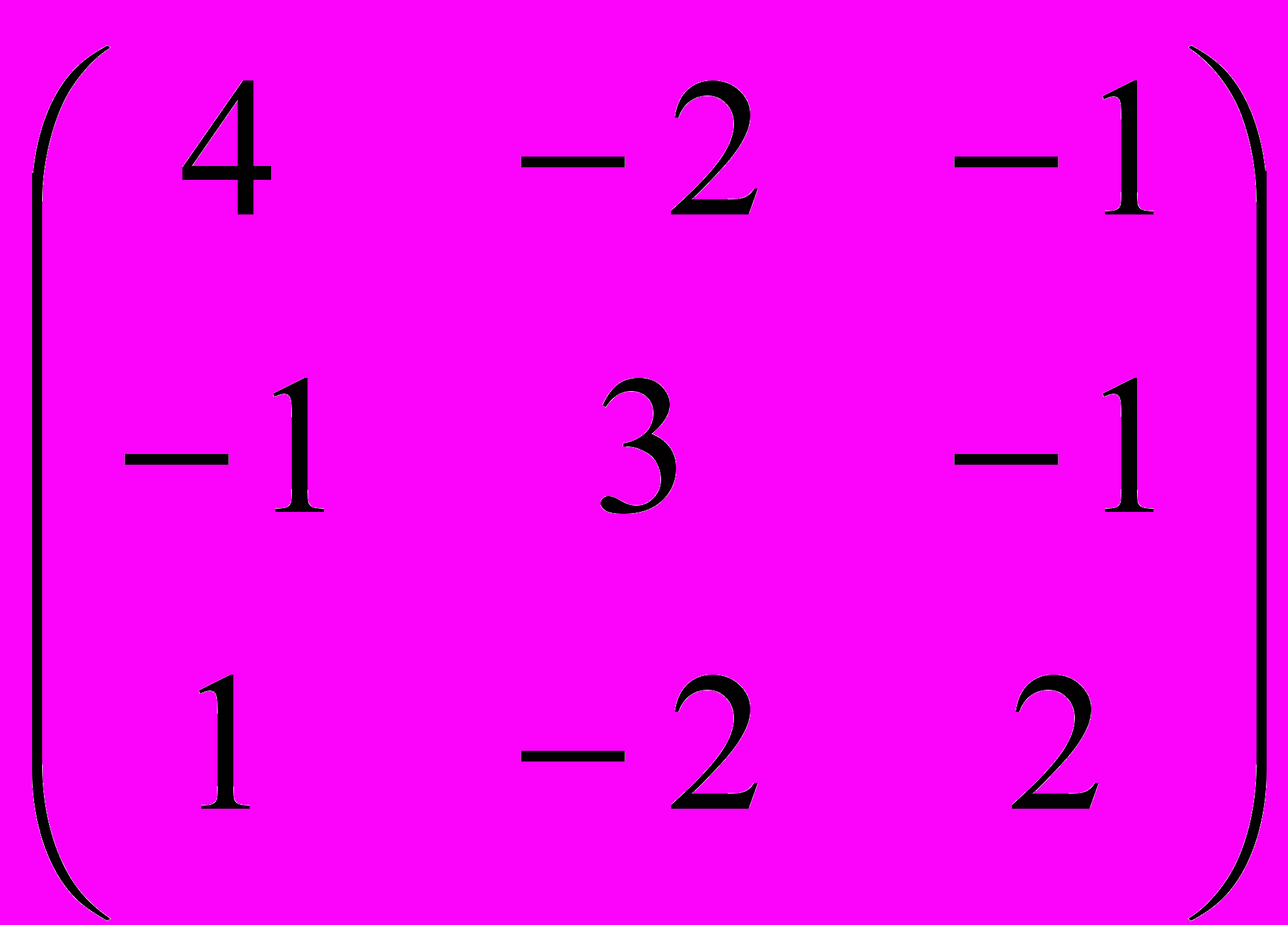16. Исследовать кривую второго порядка и построить ее:


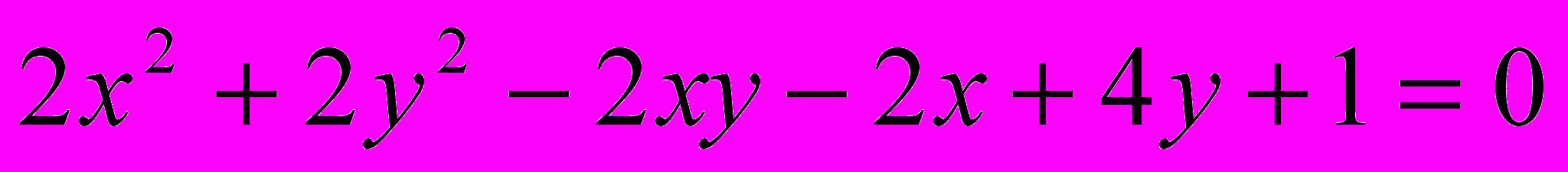
4.3. Линейная алгебра и аналитическая геометрия является одним из базовых математических курсов, преподаваемых на первом курсе, поэтому изучению этого курса должно придаваться особое значение. Главная цель курса дать студентам современные знания и хорошую практическую подготовку, необходимую будущему учителю для преподавания математики в средней школе и квалифицированного проведения факультативных курсов.

При построении лекционного курса важно продумать не только содержание, но и построение лекционного курса, логику изложения материала каждого раздела. Чтение лекционного курса должно проводиться на достаточно высоком уровне, однако строгость в изложении материала необходимо сочетать с его доступностью. Особое внимание необходимо обратить на прочность получаемых студентами знаний, так как при изучении данного курса закладывается база математических знаний.

Текущий контроль результатов освоения курса проводится на практических занятиях. В начале некоторых практических занятий рекомендуется проводить небольшие (минут на 10-15) самостоятельные работы по теоретическим вопросам, относящимся к теме занятия. Особое внимание необходимо уделить знанию основных определений, теоретических фактов, формул. В качестве основных задачников используются задачники Клетеника Д.В. и Кузнецова Л.А. Для выполнения домашних заданий рекомендуется иметь специальные тетради, которые регулярно проверяются. Результаты проверки фиксируются преподавателем и учитываются при промежуточных аттестациях студентов.

Кроме традиционной контрольной работы студентам предполагаются индивидуальные домашние задания по Кузнецову Л.А. (типовые расчеты стр. 142 №1-14, стр. 155 №3,5,9,12). Проверка и защита индивидуальных заданий осуществляется в часы самостоятельной работы.

Зачет по курсу выставляется, если выполнены все самостоятельные и индивидуальные задания, контрольная работа и получены положительные ответы на теоретические вопросы.


5. Перечень форм и методов самостоятельной работы


Успешное освоение курса требует напряженной самостоятельной работы студента. В программе курса приведено минимально необходимое время для работы студента над темой. Самостоятельная работа включает в себя чтение рекомендованной литературы, решение задач, предлагаемых студентам на лекциях и практических занятиях, разбор проблемных ситуаций, написание рефератов по отдельным темам. руководство и контроль за самостоятельной работой студента осуществляется в форме индивидуальных консультаций.


6. Формы текущего, промежуточного и итогового контроля.

Текущий контроль:

- Самостоятельные работы

- Индивидуальные задания

- Опрос студентов

Промежуточный контроль:

- Контрольная работа

Итоговый контроль:

- Зачет


7. Список литературы

Основная литература

1. Ефимов Н.В. Краткий курс аналитической геометрии. М.: Просвещение, 1969

2. Беклемешев Д.В.. Курс аналитической геометрии и линейной алгебры. М.: ФМЛ. 2000 (2002, 2003).

3. Кострикин. А.И. Введение в алгебру: Учеб-к для вузов. - М.: Физ-мат. лит-ра. Ч. 2: Линейная алгебра. - 2000.

4. Ильин В.А., Позняк Э.К. Аналитическая геометрия. М.: Наука. 1981.

5. Ильин В.А., Э.К. Позняк. Линейная агебра. Москва.: Н. 1984

6. Куликов Л.Я. Алгебра и теория чисел. М. Высшая школа. 1979.

7. Клетеник Д.В. Сборник задач по аналитической геометрии. М.: Наука. 1986.

8. Кузнецов Л.А. Сборник заданий по высшей математике. Типовые расчеты. – М.: Высшая школа, 1994.

Дополнительная литература

1. Мальцев А.И. Основы линейной алгебры. – М., Наука, 1970.

2. Проскуряков И.В.Сборник задач по линейной алгебре: [Учеб. пособие для физ. Мат. спец. Вузов]- 8-е изд.- М.: Лаборатория Базовых знаний, 2001.