Курс лекций для специальности 140104 «Промышленная теплоэнергетика» москва 2011
| Вид материала | Курс лекций |
- Курс лекций для специальности 140104 «Промышленная теплоэнергетика» москва 2011, 1206.2kb.
- Курс лекций для студентов специальности 140104 «Промышленная теплоэнергетика» москва, 1244.1kb.
- Курс лекций для студентов специальности 140104 «Промышленная теплоэнергетика» москва, 877kb.
- Курс лекций для студентов специальности 140104 «Промышленная теплоэнергетика», 1246.47kb.
- Рабочая программа для студентов Vкурса по специальности 140104 промышленная теплоэнергетика, 69.12kb.
- Рабочая программа для студентов IV курса специальности 100700 промышленная теплоэнергетика, 243.31kb.
- Рабочая программа для студентов Vкурса специальности 290800. Промышленная теплоэнергетика, 63.46kb.
- Нисаев Игорь Петрович, д т. н., профессор учебно-методический комплекс, 356.38kb.
- Нисаев Игорь Петрович, д т. н., профессор учебно-методический комплекс, 329.37kb.
- Учебно-методический комплекс по дисциплине «экономика» Для студентов специальностей:, 1055.87kb.
2.2. Режимы работы печи
Количество теплоты, получаемой загрузкой в течение элементарного промежутка времени в условиях теплообмена излучением:
, (2.29)где Тп, Тз – текущая температура печи и загрузки соответственно;
спр – приведенный коэффициент излучения системы печь–загрузка;
Fз – площадь тепловоспринимающей поверхности загрузки.
Приведенный коэффициент излучения системы «выпуклое тело (загрузка) внутри полого тела (рабочее пространство печи)»:
, (2.30)где Fст – площадь излучающей поверхности стен камеры печи;
εз – коэффициент черноты загрузки;
εп – коэффициент черноты камеры печи.
2.2.1. Режим нагрева
Воспринятая загрузкой теплота dQ расходуется на ее разогрев от температуры Тн до температуры Тк, прохождение химических реакций и фазовых превращений. Решение получаемого уравнения теплового баланса относительно времени разогрева или температуры загрузки в заданное время не представляется возможным. Это объясняется тем, что во времени изменяются температуры печи и загрузки, в свою очередь от Тз зависят теплофизические свойства загрузки: теплоемкость и теплопроводность. В объеме загрузки происходят химические и фазовые превращения, приводящие к поглощению или выделению энергии и изменению теплофизических характеристик системы, а в некоторых случаях и к изменению массы загрузки. Теории, учитывающей кинетику этих изменений, в настоящее время нет.
Достаточно подробно разработана теория расчета времени прогрева и температуры загрузок, в которых вся поглощенная теплота расходуется только на нагрев:
. (2.31)2.2.2. Разогрев теплотехнически «тонкой» загрузки
Если принять постоянным во времени полезный тепловой поток, т. е. Nпол = const (Nпол = Nз + Nвсп), а температуру по всему объему загрузки считать одинаковой Тз (случай теплотехнически «тонкой» загрузки), тогда имеем:
, (2.32)где
– время прогрева загрузки от Тн до Тк при Nпол = = const, с; Тн, Тк – начальная и конечная температуры загрузки соответственно.
Из уравнения (2.32) видно, что подъем температуры происходит с постоянной скоростью.
Если принять постоянной во времени температуру печи Тп и соотношение
, тогда совместное решение уравнений (2.29) и (2.31) для «тонких» загрузок дает:
; (2.33)
, (2.34)где
– время прогрева загрузки от Тн до Тк при Тп = = const.По данным уравнениям несложно рассчитать время прогрева загрузки до различных температур (например, через каждые 50, 100 или 200 градусов) и построить кривую нагрева Тз = f(t). Можно показать, что нагрев «тонкой» загрузки до Т =0,65Тп происходит практически с постоянной скоростью, т. е. с постоянным тепловым потоком, воспринимаемым загрузкой.
Графически изменения температур и тепловых потоков при нагреве изделий в режимах Nпол = const и Тп = const изображены на рис. 2.4 и 2.5.
Режим нагрева при постоянном тепловом потоке Nпол = const реализуется тогда, когда изделия загружают в холодную (частично остывшую) печь и нагревают совместно с нею, установив мощность Nпол. После достижения печью заданной температуры Тп прогрев загрузки из режима Nпол = const переходит в режим при постоянной температуре печи (которую поддерживают автоматические регуляторы температуры). При этом печь начинает потреблять меньшую мощность, а после достижения загрузкой температуры Тк = Тп, потребляемая ЭПС мощность расходуется только для компенсации тепловых потерь (рис. 2.5).
Если в садочную печь, разогретую до Тп, внести холодную загрузку, то она воспримет тепловой поток от внутренней поверхности печи qСо:
, (2.35)где qСо – тепловой поток от внутренней поверхности печи к загрузке;
Тн – температура холодной загрузки.
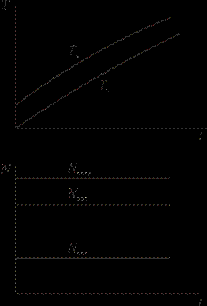
Рис. 2.4. Режим нагрева загрузки при Nпол = const
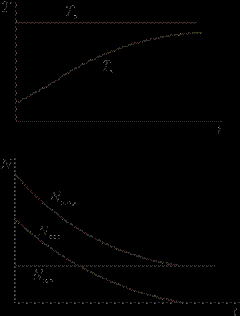
Рис. 2.5. Режим нагрева загрузки при Тп = const
Следовательно, удержать исходную температуру в печи на заданном прежде уровне можно только при условии, что нагревательные элементы выделяют тепловой поток qСо, иначе температура печи снизится и работа перейдет в режим Nпол = const. Можно определить температуру поверхности загрузки
, начиная с которой снова будет обеспечено условие Тп = const:
, (2.36)где qmax – максимальная интенсивность теплового потока к загрузке.
Время нагрева загрузки до
считают из условия Nпол = const, в дальнейшем нагрев происходит в режиме Тп = const.2.2.3. Время разогрева ЭПС
Для садочных печей сопротивления иногда важно знать время tр, необходимое для разогрева пустой печи до заданной температуры Тп. Его можно определить по уравнению:
, (2.37)где Qак – тепло, аккумулированное конструкцией печи;
Nср – средняя мощность нагревателя в период разогрева;
Nпот.ср – средние тепловые потери в период разогрева.
Для расчета принимают:
; (2.38)
, (2.39)где Nу – установленная мощность печи;
Nпот – тепловые потери в установившемся режиме.
2.2.4. Разогрев теплотехнически «массивной» загрузки
Расчет tн усложняется, если учесть градиент температур по объему загрузки. Загрузки, представляющие собой объемные изделия или массу материала, загруженного в тигель или лодочку, следует относить к теплотехнически «массивным», для них характерно наличие перепада температур между поверхностью и центром загрузки в установившемся режиме нагрева. Строго теплотехнически «массивными» считают загрузки, для которых число Био больше 0,50:
, (2.40)где a – коэффициент теплоотдачи;
l – коэффициент теплопроводности;
– расчетный размер загрузки, ( = R – для шара или цилиндра радиуса R; = S – для пластины толщиной 2S при симметричном нагреве; = 2S – при одностороннем нагреве пластины).Нагрев «массивной» загрузки определяется не только внешней теплопередачей от печи к нагреваемой поверхности, но и характером распределения тепла внутри загрузки. В режиме Nпол = const процесс нагрева «массивной» загрузки можно разбить на три этапа: на первом этапе происходит разогрев поверхности и центра с различными скоростями, и в конце этого этапа устанавливается постоянный перепад температур между ними:
; 
, (2.41)где
, 
– установившийся перепад температур в пластине или цилиндре соответственно; q – тепловой поток, воспринимаемый загрузкой.
, (2.42)где Тпов – температура поверхности загрузки;
Тцентр – температура на средней плоскости пластины или на оси цилиндра.
К концу первого этапа имеем:
, 
; (2.43)
, 
; (2.44)
, 
, (2.45)где tн1 – время первого этапа нагрева;
– коэффициент температуропроводности; r – плотность загрузки.
На втором этапе наступает «регулярный» режим, при котором температура растет во всех точках с постоянной скоростью, при этом перепад температур ΔТс остается неизменным:
, 
; (2.46)
; (2.47)
; (2.48)
, (2.49)где vс – скорость увеличения температуры на втором этапе, К/с;
tн.2 – время второго этапа нагрева.
Второй этап завершается, когда температура поверхности загрузки Тпов.2 достигнет заданного значения.
Если установившийся перепад температур ΔТс недопустим, то необходимо выровнять температуры в центре и на поверхности загрузки. Это происходит на третьем этапе нагрева. Выровнять температуры до заданного перепада ΔТзад можно двумя путями.
1. Если по технологическим соображениям допустим перегрев поверхности на
(для пластины) или 
(для цилиндра), тогда можно продолжить второй этап до этого момента, а затем прекратить подвод тепла к загрузке. В результате температура поверхности будет снижаться, а температура в центре расти, т. е. перепад температур будет уменьшаться. На рис. 2.6 и 2.7 приведены графики выравнивания температур в этом режиме.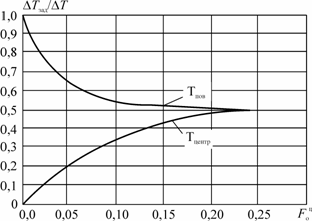
Рис. 2.6. График выравнивания температур в цилиндре
без подвода мощности при предварительном перегреве поверхности
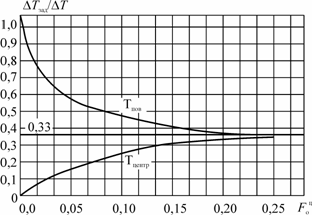
Рис. 2.7. График выравнивания температур в пластине
без подвода мощности при предварительном перегреве поверхности
Для определения времени выравнивания температур до заданного перепада ΔТзад, находят отношение
. Затем на графике определяют такое значение числа Фурье 
– для пластины, 
– для цилиндра:
; 
, (2.50)при котором расстояние между кривыми Тпов и Тцентр равно отношению
. По найденному К рассчитывают время выравнивания температур:
; 
. (2.51)2. Второй способ выравнивания температур до заданного перепада ΔТзад заключается в нагреве загрузки при постоянной температуре поверхности и постепенном снижении интенсивности теплового потока, воспринимаемого поверхностью загрузки.
Графики этого процесса приведены на рис. 2.8 и 2.9. Их используют для определения tнз таким же образом, как и графики 2.6 и 2.7. Отличие заключается в том, что линия температуры поверхности – это горизонтальная прямая.
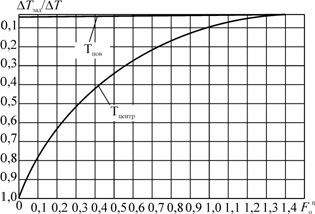
Рис. 2.8. График выравнивания температур в пластине при
подводе мощности без предварительного перегрева поверхности
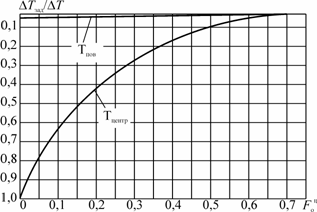
Рис. 2.9. График выравнивания температур в цилиндре при
подводе мощности без предварительного перегрева поверхности
В целом время нагрева «массивной» загрузки в режиме Nпол = const находим как сумму времен каждого этапа нагрева:
. (2.52)С достаточной точностью, опуская промежуточные расчеты tн.1, tн.2 и tн.3, время нагрева можно определить по уравнению:
, (2.53)где Тк – заданная номинальная температура нагрева;
Тн – начальная температура загрузки.
Расчет процесса нагрева «массивных» загрузок в режиме Тпол = const сводится к следующему.
1. Определяют число Био для загрузки:
; 
, (2.54)где Biц – число Вi для цилиндра;
Biп – число Вi для пластины;
a – коэффициент теплоотдачи;
l – коэффициент теплопроводности.
Коэффициент теплоотдачи излучением зависит от температуры поверхности загрузки и, следовательно, изменяется в процессе нагрева:
, (2.55)поэтому рекомендуется в начале расчета определить средний коэффициент теплоотдачи. При нагреве от температуры приблизительно 0 С до Тпов.з, близкой к Тп:
. (2.56)2. Находят коэффициенты d2, m2, Р, Ро, N, Nо в табл. 2.1.
| Таблица 2.1 Коэффициенты для расчета относительных температур в режиме нагрева Тп = const
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3. Рассчитывают относительные температуры центра и поверхности изделия:
; 
; (2.57)
; 
, (2.58)где
– относительная температура центра цилиндра; 
– относительная температура центра пластины; 
– относительная температура поверхности цилиндра; 
– относительная температура поверхности пластины.Уравнения (2.57) и (2.58) справедливы, если число Фурье для цилиндра больше 0,3, а для пластины больше 0,25.
4. Находят абсолютные температуры:
; (2.59)
, (2.60)где Тп – температура печи;
Тн – температура загрузки в начале нагрева.
5. Строят кривые нагрева Тцентр = f(t) и Тпов= f(t).
В результате расчета находят время
, необходимое для нагрева загрузки до заданных Тпов и Тцентр.