Кр вуз фпт

Вид материала

Конспект

Содержание План лекции Фиксированная запятая (точка). Плавающая запятая (точка). М — мантисса числа (│М 1.7. Алгебраическое представление двоичных чисел Обратный код Дополнительный код 2.1 Логические элементы и узлы ЭВМ Логические операции и базовые элементы компьютера Логические операции 2.2 Классификация элементов и их сравнительная характеристика Элементы цифрового устройства Физически полная система элементов Технически полная система элементов Элементом цифровой схемотехники По параметрам 2.3 Общие характеристики элементов логических устройств 2. Динамические параметры Задержка распространения сигнала при переходе выходного напряжения от "1" к "О" Задержка распространения сигнала при переходе выходного напряжения от "0" к "1" ... Полное содержание

Подобный материал:

• К вопросу о создании асу вуз: Проблемы создания и внедрения, 16.08kb.
• Программа : Учебная программа имеет модульную структуру и состоит из: обязательных, 93.82kb.
• Работа выполнена в научно-исследовательском секторе Школы-студии (вуз) им. Вл. И. Немировича-Данченко, 7376.04kb.
• Д. Е. Бурланков Все физические явления разворачиваются в пространстве с течением времени:, 268kb.
• В г. Ростове-на-Дону > I. Общие положения нир является одним из основных направлений, 69.33kb.
• Преемственность в обеспечении непрерывного экономического образования в системе «школа-ссуз-вуз», 463.36kb.
• Всероссийский конкурс «директор школы 2010» Принятие управленческих решений в организации, 816.08kb.
• Сегодня дпи нгту единственный в Нижегородском регионе вуз, где готовят инженеров химического, 79.68kb.
• Instituto Superior Tecnico крупнейший, наиболее престижный инженерный вуз Португалии,, 14.38kb.
• Гневашева В. А. Российский студент: социальный облик. По материалам мониторинга «Российский, 1950.72kb.

Тема 1: Формы изображения информации

План лекции:

• Представление чисел в ЭВМ
  
• Алгебраическое представление двоичных чисел
  

1.6. Представление чисел в ЭВМ

Как известно, в ЭВМ применяется двоичная система счисления. Может быть доказано, что при этом на построение ЭВМ тратится наименьшее количество базовых аппаратных элементов — «венти­лей». Точнее, оптимальным основанием системы счисления по кри­терию «минимум аппаратных расходов» является основание нату­рального логарифма е= 2,72.

Однако по ряду очевидных причин для ЭВМ принято Р=2. Достаточно вспомнить, что одна из первых электронных ВМ ENIAC содержала 17 468 электронных ламп, имела размеры около 6 м в высоту и 30 м в длину. Обилие применяемых вакуумных ламп, габаритные размеры машины отчасти объяснялись тем, что она ра­ботала с десятичными числами.

В ЭВМ применяются две формы представления чисел:

• естественная форма, или форма с фиксированной запятой (точкой) - ФЗ (ФТ);
  
• нормальная форма, или форма с плавающей запятой (точ­кой) — ПЗ (ПТ).
  

Фиксированная запятая (точка). В форме представления с фикси­рованной запятой (точкой) числа изображаются в виде последова­тельности цифр с постоянным для всех чисел положением запятой, отделяющей целую часть от дробной.

Например, пусть числа представлены в десятичной системе счисления и имеют пять разрядов в целой части числа (до запятой) и пять в дробной части (после запятой).

Числа, записанные в такую разрядную сетку, имеют вид:

+00721.35500.

+00000.00328.

-10301.20260.

Эта форма наиболее проста, естественна, но имеет небольшой диапазон представления чисел и поэтому чаще всего неприемлема при вычислениях.

Диапазон значащих чисел N в системе счисления с основанием Р при наличии т разрядов в целой части и s разрядов в дробной части числа (без учета знака числа) будет таким:

P^-s ≤ N≤ P^m – Р^-s

Например, при Р=2, m=10 и s = 6 числа изменяются в диапазо­не 0,015 < N< 1024. Если в результате операции получится число, выходящее за допустимые пределы, произойдет переполнение раз­рядной сетки, и дальнейшие вычисления теряют смысл. В современных компьютерах естественная форма представления использу­ется как вспомогательная и только для целых чисел.

В памяти ЭВМ числа с фиксированной точкой хранятся в трех форматах:

а) полуслово — 16 бит, или 2 байта;

б) слово — 32 бита, или 4 байта;

в) двойное слово — 64 бита, или 8 байтов.

Отрицательные числа с ФТ записываются в разрядную сетку в дополнительных кодах, которые образуются прибавлением единицы к младшему разряду обратного кода. Обратный код получается за­меной единиц на нули, а нулей на единицы в прямом двоичном коде.

Плавающая запятая (точка). В форме представления с плаваю­щей запятой (точкой) число изображается в виде двух групп цифр:

• мантисса;
  
• порядок.
  

При этом абсолютная величина мантиссы должна быть мень­ше 1, а порядок должен быть целым числом. В общем виде число в форме с плавающей запятой может быть представлено так:



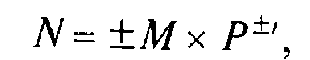
где М — мантисса числа (│М││\тественна, но имеет небольшой"< I); r— порядок числа (целое число); Р — основание системы счисления.

Например, приведенные ранее числа в нормальной форме запи­шутся следующим образом:

+0,721355 х 10³;

+0,328 х 10 ^-3;

-0,103012026 х 10⁵.

Нормальная форма представления обеспечивает большой диапа­зон отображения чисел и является основной в современных компь­ютерах. Так, диапазон значащих чисел в системе счисления с осно­ванием Р при наличии т разрядов у мантиссы и s разрядов у поряд­ка (без учета знаковых разрядов порядка и мантиссы) будет:



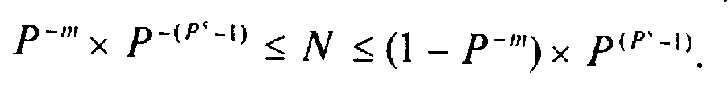
Например, при P = 2, т = 22 и s= 10 диапазон чисел простирает­ся примерно от 10^-300 до 10³⁰⁰. Для сравнения: количество секунд, которые прошли с момента образования планет Солнечной систе­мы, составляет около 10¹⁸.

Следует заметить, что все числа с плавающей запятой хранятся в машине в так называемом нормализованном виде.

Нормализованным называют такое число, старший разряд ман­тиссы которого больше нуля. У нормализованных двоичных чисел, следовательно, 0,5 < │М│< I.

Нормализованные, т. е. приведенные к правильной дроби, числа:

10,35₁₀ = 0,1035₁₀ x 10⁺²;

0,00007245₈ = 0,7245₈ х 8 ^-4;

F5C,9B₁₆ = 0,F5C9B₁₆ x 16⁺³;

В памяти ЭВМ числа с ПТ хранятся в двух форматах:

• слово — 32 бита, или 4 байта;
  
• двойное слово — 64 бита, или 8 байт.
  

Разрядная сетка для чисел с ПТ имеет следующую структуру:

• нулевой разряд — это знак числа (0 — «минус», 1 — «плюс»);
  
• с 1 по 7 разряд записывается порядок в прямом двоичном коде, пустые разряды заполняются нулями. В первом разряде указывается знак порядка (1 — «плюс» или 0 — «минус»);
  
• с 8 по 31 (63) указывается мантисса, слева направо без нуля целых в прямом двоичном коде и для отрицательных чисел и пустые разряды заполняются нулями.
  

1.7. Алгебраическое представление двоичных чисел

Знак числа обычно кодируется двоичной цифрой, при этом:

• код 0 означает знак + (плюс);
  
• код 1 — знак - (минус).
  

Для алгебраического представления чисел, т. е. для представле­ния чисел с учетом их знака, в вычислительных машинах использу­ются специальные коды:

• прямой код числа;
  
• обратный код;
  
• дополнительный код.
  

При этом два последних кода позволяют заменить неудобную для компьютера операцию вычитания на операцию сложения с от­рицательным числом. Дополнительный код обеспечивает более бы­строе выполнение операций, поэтому в компьютере чаще всего при­меняется именно он.

Пример:

Число Прямой код Обратный код Дополнительный код

Х= +0,10101 [Х]_пр= 0,10101 [Х]_0Б = 0,10101 [Х]_доп = 0.10101

Y= -0,01011 [У]_пр= 1,01011 [Y]_об= 1.10100 [У]_доп = 1.10101


Прямой код

Если при сложении в ЭВМ оба слагаемых имеют одинаковый знак, то операция сложения выполняется обычным путем. Если при сложении слагаемые имеют разные знаки, то сначала необходимо выявить большее по абсолютной величине число, из него произве­сти вычитание меньшего по абсолютной величине числа и разности присвоить знак большего числа.

Выполнение операций умножения и деления в прямом коде вы­полняется обычным образом, но знак результата определяется по совпадению или несовпадению знаков участвовавших в операции чисел.

Операцию вычитания в этом коде нельзя заменить операцией сложения с отрицательным числом, поэтому возникают сложности, связанные с займом значений из старших разрядов уменьшаемого числа. В связи с этим прямой код в ЭВМ почти не применяется.

Обратный код

Для того чтобы получить обратный код отрицательного числа, необходимо все цифры этого числа инвертировать, т. е. в знаковом разряде поставить 1, во всех значащих разрядах нули заменить еди­ницами, а единицы нулями.

Например, для N = 1011, [N]_обр = 0,1011

для N = -1011, [N]_обр = 1,0100

Дополнительный код.

Для того чтобы получить дополнительный код отрицательного числа, необходимо все его цифры инвертировать (в знаковом разря­де поставить единицу, во всех значащих разрядах нули заменить единицами, а единицы — нулями) и затем к младшему разряду при­бавить единицу. В случае возникновения переноса из первого после запятой разряда в знаковый разряд к числу следует прибавить еди­ницу в младший разряд.

Например, для N =+1011, [N]_доп = 0,1011,

для N = -1100, [N]_доп = 1,0100,

для N = -0000, [N]_доп = 10,0000 = 0,0000 (1 исчезает).

Неодно­значности в изображении 0 нет

Эмпирическое правило: для получения дополнительного кода отрицательного числа необходимо все символы этого числа инвер­тировать, кроме последней (младшей) единицы и тех нулей, кото­рые за ней следуют.

Пример:

а) Прямой код Обратный код Сложение
[х]_пр=0,10101 0,10101 0,10101
[у]_пр=1.01001 1,10110 1,10110

[х+у]_пр=0,01100 10,01011

1

х+у = 0,01100

Проверим в десятеричном коде эквивалентными целыми числами:

х = +21; у = -9; х + у = +12 = 01100₍₂₎

б) Прямой код Обратный код Сложение
[х]_пр=1,10101 1,01010 1,01010

[y]_пр=0,01001 0,01001 0,01001

[х+у]_пр=1,01100 1,10011

[х+у]_об = 1,10011

Проверка: х = -21; у = +9; х + у = -12 = 1,01100₍₂₎

в) Прямой код Сдвиг Дополнительный код Сложение
[х]_пр=1,11010 1,011010 1,100110 1,100110
[y]_пр=1.01100 1,001100 1,110100 1,110100

[х+у]_доп =11,011010

Проверка: х = -26; y = -12; х + в = -38 = 1,100110₍₂₎

Для того чтобы избежать ошибок при выполнении бинарных операций, перед переводом чисел в обратные и дополнительные коды необходимо выравни­вать количество разрядов прямого кода операндов.


При сложении чисел, меньших единицы, могут быть получены числа, по абсо­лютной величине больше единицы. Для выявления переполнения разрядной сетки в ЭВМ применяются модифицированные прямой, обратный и дополни­тельный коды. В этих кодах знак кодируется двумя разрядами, причем знаку "плюс" отвечает комбинация 00, а знаку "минус" — комбинация 11.

Правила сложения для модифицированных кодов те же, что и для обычных. Единица переноса из старшего знакового разряда в модифицированном до­полнительном коде отбрасывается, а в модифицированном обратном коде передается в младший цифровой разряд.

Признаком переполнения служит появление в знаковом разряде суммы ком­бинации 01 при сложении положительных чисел (положительное переполне­ние) или 10 при сложении отрицательных чисел (отрицательное переполне­ние). Старший знаковый разряд в этих случаях содержит истинное значение знака суммы, а младший является старшей цифрой значащего числа. Для коррекции переполнения число надо сдвинуть в разрядной сетке на один раз­ряд вправо, а в старший знаковый разряд, который освободился, поместить цифру, равную новому значению младшего знакового разряда. После кор­ректирования переполнения мантиссы результата необходимо увеличить на единицу порядок результата.

Пример:

Сложение Х= 0,101011

+ Y= 0.110100

X+Y= 1,011111

Сложение в модифицированном коде:

Х= 00,101011

+ Y= 00.110100

X+Y= 01,011111 -> 00,1011111


Контрольные вопросы

1. Как изображаются числа с фиксированной запятой.
   
2. Как изображаются числа с плавающей запятой
   
3. Как представляются двоичные числа в алгебраическом виде.
   
4. Расскажите о назначении и функционировании кодов двоичных чисел (прямой, обратный, дополнительный).
   
5. Как выполняются арифметические действия в двоичной системе.
   
6. Как представляются отрицательные числа в двоичном коде?
   
7. Используя двоичные коды, определите разность десятичных чисел 24 и 56.
   
8. Что такое нормализация чисел и переполнения разрядной сетки ЭВМ?
   
9. Приведите правила образования обратного и дополнительного кода.
   
10. Используя двоичные коды, определите разность десятичных чисел -12 и 8.
    

Лекция 4

Тема 2: Схемотехника логических элементов

План лекции:

• Логические элементы и узлы ЭВМ.
  
• Классификация элементов и их сравнительная характеристика
  
• Общие характеристики элементов цифровых устройств
  

2.1 Логические элементы и узлы ЭВМ

Начало исследованиям в области формальной логики было по­ложено работами Аристотеля в IV в. до нашей эры. Однако матема­тические подходы к этим вопросам впервые были указаны Дж. Бу­лем. В честь него алгебру высказывания называют булевой алгеброй, а логические значения — булевыми. Основу математической логики составляет алгебра высказываний. Это освобождает матлогику от неопределенности в толковании логических выражений, показы­вающих связь между отдельными суждениями и понятиями. Алгебра логики используется при построении основных узлов ЭВМ (дешиф­ратор, сумматор, шифратор).

Алгебра логики оперирует с высказываниями. Под высказыва­нием понимают повествовательное предложение, относительно ко­торого можно утверждать, истинно оно или ложно. Например, вы­ражение «Расстояние от Москвы до Киева больше, чем от Москвы до Тулы» истинно, а выражение «5 < 2» — ложно.

Высказывания принято обозначать буквами латинского алфави­та: А, В, С, ..., X, У и т. д. Если высказывание С истинно, то пишут С= 1 (C=t, true), а если оно ложно, то С= О (С=f, false).

Логические операции и базовые элементы компьютера

Наиболее часто использу­ются логические операции, выражаемые словами «НЕ», «И», «ИЛИ».

Логический элемент — это часть электронной схе­мы, которая реализует элементарную логическую функцию.

Логическими элементами компьютеров являются электронные схемы И, ИЛИ, НЕ, И-НЕ, ИЛИ-НЕ и другие (называемые обыч­но вентилями), а также триггер.

С помощью этих схем можно реали­зовать любую логическую функцию, описывающую работу уст­ройств компьютера.

Обычно у вентилей бывает от двух до восьми входов и один или два выхода.

На структурных схемах ЭВМ каждый логический элемент имеет свое условное обозначение, которое выражает его логическую функ­цию, но не указывает на то, какая именно электронная схема в нем реализована. Работу логических элементов описывают с помощью таблиц истинности.

Логические операции.

Рассмотрим логические операции и соот­ветствующие им элементы логических схем.

Конъюнкция.

Соединение двух (или нескольких) высказы­ваний в одно с помощью союза И называется операцией логи­ческого умножения, или конъюнкцией.

Эту операцию принято обо­значать знаками «, &» или знаком умножения «х».

Сложное выска­зывание Х & Y истинно только в том случае, когда истинны оба входящих в него высказывания.

Истинность такого высказывания задается табл.2.1

Табл. 2.1 Таблица истинности конъюнкции

х	y	X & Y
0	0	0 (ложно)
1	0	0 (ложно)
0	1	0 (ложно)
1	1	1 (истинно)

Логическая схема И реализует конъюнкцию двух или более логи­ческих значений.

Условное обозначение на структурных диаграммах схемы И с двумя входами представлено на рис. 2.1, а.



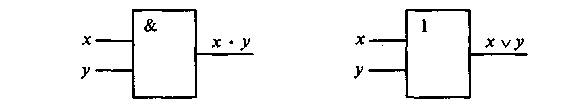
а) б)

Рис. 2.1 Условное обозначение схемы: а) И; б) ИЛИ

Единица на выходе схемы И будет тогда и только тогда, когда на всех входах будут единицы. Когда хотя бы на одном входе будет нуль, на выходе также будет нуль.

Связь между выходом z этой схемы и входами х и у описывается соотношением: z = x & у (читается как «х И у»). Операция конъюнк­ции на структурных схемах обозначается знаком «&».

Дизъюнкция.

Объединение двух (или нескольких) высказы­ваний с помощью союза ИЛИ называется операцией логиче­ского сложения, или дизъюнкцией.

Эту операцию обозначают, зна­ками «|, v» или знаком сложения «+».

Сложное высказывание A v В истинно, если истинно хотя бы одно из входящих в него высказыва­ний (табл. 2.2).

Табл. 2.2 Таблица истинности дизъюнкции

х	y	X v Y
0	0	0 (ложно)
1	0	1 (истинно)
0	1	1 (истинно)
1	1	1 (истинно)

Схема ИЛИ реализует дизъюнкцию двух или более логических значений. Когда хотя бы на одном входе схемы ИЛИ будет единица, на ее выходе также будет единица.

Условное обозначение на структурных схемах схемы ИЛИ с дву­мя входами представлено на рис. 2.1, б. Знак «1» на схеме — от классического обозначения дизъюнкции как «≥1» (т. е. значение дизъюнкции равно единице, если сумма значений операндов боль­ше или равна 1).

Связь между выходом z этой схемы и входами х и у описывается соотношением: z = x v у (читается как «х ИЛИ у»).

Инверсия.

Присоединение частицы НЕ к некоторому высказыванию называется операцией отрицания (инверсии) и обо­значается А (или -А).

Если высказывание А истинно, то В ложно, и наоборот (табл. 2.3).

Табл. 2.3 Таблица истинности инверсии.

А	А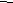
1	0 (ложно)
0	1 (истинно)

Схема НЕ (инвертор) реализует операцию отрицания. Связь ме­жду входом х этой схемы и выходом z можно записать соотношени­ем z = х, где х читается как «НЕ х» или «ИНВЕРСИЯ х».

Если на входе схемы «О», то на выходе «1», и наоборот.

Услов­ное обозначение на структурных схемах инвертора — на рис. 2.2, в.



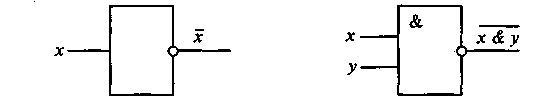
в) г)

Рис. 2.2

Вентили.

Кроме схемных элементов, соответствующих перечис­ленным логическим операторам, в состав логических схем входят комбинированные связки, именуемые вентилями, например сле­дующие.

Схема И—НЕ состоит из элемента И и инвертора и осуществля­ет отрицание результата схемы И (табл. 2.4).

Табл. 2.4 Таблица истинности схемы И-НЕ.

х	y	X & Y
0	0	1 (истинно)
1	0	1 (истинно)
0	1	1 (истинно)
1	1	0 (ложно)

Связь между выходом Z и входами х и у схемы записывают как х & у, или «ИНВЕРСИЯ х И у». Условное обозначение на структурных схемах схемы И—НЕ с двумя входами представлено на рис. 2.2, г.

Схема ИЛИ—НЕ состоит из элемента ИЛИ и инвертора и осу­ществляет отрицание результата схемы ИЛИ (табл. 1.19).

Табл. 2.5 Таблица истинности схемы ИЛИ-НЕ.

х	y	X v Y
0	0	1 (истинно)
1	0	0 (ложно)
0	1	0 (ложно)
1	1	0 (ложно)

С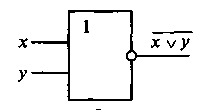вязь ме­жду выходом z и входами х и у схемы записывают как х v у, или «ИНВЕРСИЯ х ИЛИ у». Условное обозначение на структурных схе­мах схемы ИЛИ—НЕ с двумя входами представлено на рис. 2.3.


Рис. 2.3

2.2 Классификация элементов и их сравнительная характеристика

Цифровое устройство — это устройство, предназначенное для приема, обработки и выдачи цифровой информации. Любое цифровое устройство с произвольными мерой сложности и назначением выполняется на дискретных элементах, кото­рые включают в себя интегральные схемы разной степени интеграции. Незави­симо от функционального назначения элементов их схемотехнологические реализации владеют рядом общих параметров и характеристик, которые опре­деляют их работу в статическом и динамическом режимах.

Элементы цифрового устройства — наименьшие функциональные части, на которые разбивается устройство при его логическом проектировании и техни­ческой реализации. Поскольку принято считать, что наименьшие функцио­нальные части цифрового устройства выполняют простейшие логические или вспомогательные функции, можно сказать, что элементы цифрового устройст­ва это электронные схемы, которые представляют собой некоторую совокуп­ность определенным образом соединенных компонентов и выполняют одну или несколько простейших логических или вспомогательных операций. Ком­понентами элементов цифровых устройств являются интегральные схемы раз­ной степени интеграции, транзисторы и диоды разного типа, резисторы, кон­денсаторы и индукторы.

Элементы цифровых устройств принято разрабатывать и выпускать в виде сис­тем или серий, которые включают в себя их разные модификации (см.приложение А)

Физически полная система элементов — система, которая содержит специальные элемен­ты, обеопечивающие возможность построения цепей управления, устройств памяти и цепей связи. Последние обеспечивают работу электромеханических узлов цифровых устройств типа реле, переключателей, механизмов перфора­ции, печати и т. п., а также схем связи разных узлов цифрового устройства с устройствами ввода/вывода; элементы индикации информационных состояний узлов цифрового устройства и генераторы тактовых сигналов.

Технически полная система элементов — система, которая удовлетворяет требованиям функциональной и физической полноты.

Функционально полная система элементов — система, которая позволяет реа­лизовать любые сложные функции переключения путем суперпозиции про­стейших функций, которые выполняются элементами данной серии.

Элементом цифровой схемотехники называют устройство, которое выполня­ет одну из задач реализации булевых функций: запоминание информации, преобразование, формирование и усиление сигналов. Все виды элементов цифровых устройств можно разделить на три группы: логические, функцио­нальные и вспомогательные (рис. 2.1) .

Логическим элементом называется устройство, которое реализует только од­ну булеву функцию. Такие элементы называют однофункциональными в от­личие от функциональных элементов, которые реализуют несколько булевых функций.

В функциональном элементе могут использоваться несколько ло­гических элементов. Запоминающие элементы используют в устройствах, которые сохраняют данные и программы в виде цифровых кодов.

К вспомогательным элементам относят усилительно-формирующие элементы преобразующие нестандартные сиг­налы в разных цепях цифровых устройств до уровней логических элементов, которые их обрабатывают. Кроме того, они иногда используются для увели­чения нагрузочной способности логических элементов и т. д. Специальные элементы включают в свой состав генераторы сигналов, преобразователи уровней, элементы гальванической развязки и др.



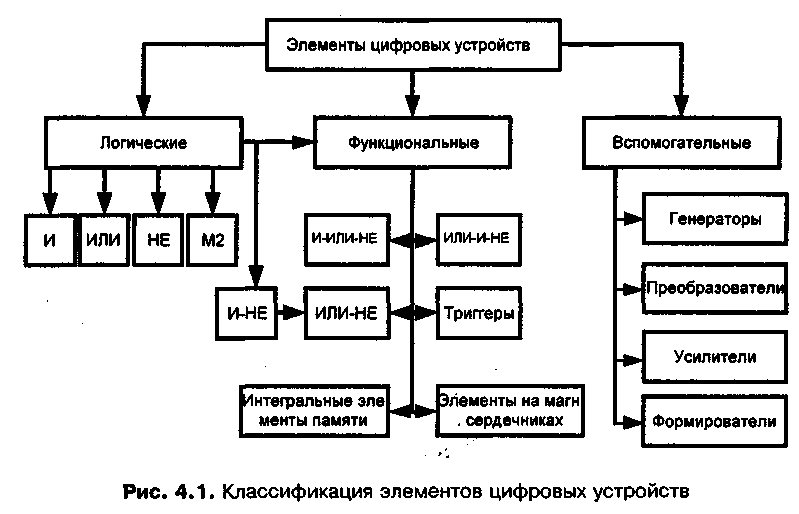
Рис. 2.1 Классификация элементов цифровых устройств

По параметрам элементы можно классифицировать в зависимости от реали­зации логических функций, нагрузочной способности, быстродействия или времени задержки, предельной рабочей частоты, помехоустойчивости и по­требляемой мощности. В зависимости от времени задержки сигнала инте­гральные микросхемы делятся на устройства высокого и сверхвысокого бы­стродействия.

По типам базовых элементов электронных ключей разделяют несколько ти­пов схем, где наиболее распространенными являются следующие:

• транзисторно-транзисторная логика (ТТЛ);
  
• эмиттерно-связанная логика (ЭСЛ);
  
• инжекционная интегральная логика (И²Л);
  
• структуры металл-оксид-полупроводник p-типа (р-МОП);
  
• структуры металл-оксид-полупроводник n-типа (п-МОП);
  
• комплементарные МОП-структуры (КМОП);
  
• динамические МОП-структуры.
  

Более старые виды схемотехники, такие как резистивно-транзисторная логи­ка (РТЛ) и диодно-транзисторная логика (ДТЛ), в микропроцессорных сис­темах практически не применяются.

Логические схемы, которые изготовляются на разной конструктивно-технологической основе, значительно различаются по своим характеристи­кам, даже если они реализуют одинаковые функции. У любого из указанных видов схемотехники имеются свои преимущества. Так, ЭСЛ отличается вы­соким быстродействием, хотя некоторые разновидности ТТЛ приближаются к ней по этому параметру. Как р-МОП-, так и n-МОП-логика широко приме­няются в микропроцессорах, а КМОП-схемотехника пользуется преимуще­ством, если важно уменьшить потребляемую мощность.

Динамические МОП-структуры используются для построения различных за­поминающих устройств; они имеют простую организацию, в которой логиче­ское состояние определяется зарядом емкости, внутренне присущей логиче­скому элементу. И²Л применяется в интегральных схемах.

2.3 Общие характеристики элементов логических устройств

1. Статические параметры определяют условия формирования и значения напряжений высокого и низкого уровней на выходе ЛЭ, его нагрузочную возможность, потребляемую мощность при заданных напряжении пита­ния, нагрузке и температуре окружающей среды.

К статическим параметрам ЛЭ относятся:

• выходные и входные напряжения логических "О" и "1" (U⁰_вых, U¹_вых, U⁰_вх, U¹_вх );

• входные и выходные пороговые напряжения логических "О" и "1"

(U⁰_{вых. пор}, U¹_{вых. пор}, U⁰_{вх. пор}, U¹_{вх. пор} );

• входные и выходные токи логических "О" и " 1" (I⁰_вх, I¹_вх, I⁰_вых, I¹_вых);
  
• токи потребления в состоянии логических "О" и " 1" (I¹_пот, I⁰_пот );
  
• потребляемая мощность (Р_пот) •
  

2. Динамические параметры. Быстродействие ЛЭ при переключении опре­деляется электрической схемой, технологией изготовления и характером нагрузки. Для идентификации измерений динамических параметров в тех­нической документации на ИС приводятся параметры эквивалентной на­грузки, устанавливаются требования к амплитуде и продолжительности фронта входного сигнала.

На рис. 2.2 показана временная диаграмма, которая объясняет изменение характеристик выходного импульса в зависимости от параметров входно­го импульса и свойств элемента.



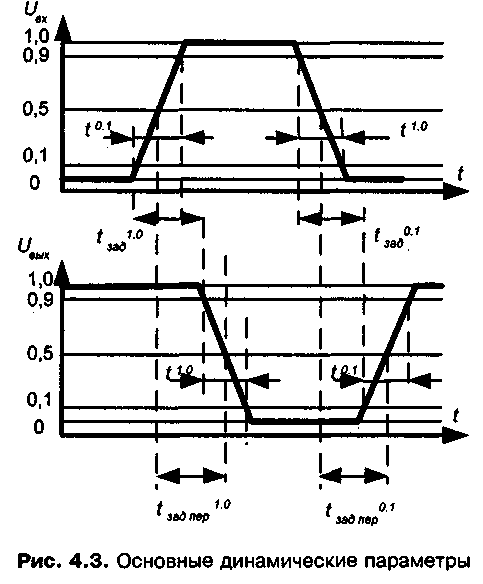
Рис. 2.2 Основные динамические характеристики

Уровни отсчета напряжений для определения динамических параметров устанавливаются относительно выходных напряжений порогов "1" и "О".

Основными динамическими параметрами ЛЭ являются: задержка рас­пространения сигнала t_3ад.п при переключении и продолжительность по­ложительного (нарастающего) и отрицательного (спадающего) фронтов выходных сигналов.

Задержка распространения сигнала при переходе выходного напряжения от "1" к "О" t^1,0 _зад.п (при положительной логике это отвечает отрицательно­му фронту, при отрицательной — положительному фронту выходного сигнала) определяется как интервал времени между входным и выходным сигналами ЛЭ, измеренный на уровне 0,5 логического перепада входного и выходного сигналов.

Задержка распространения сигнала при переходе выходного напряжения от "0" к "1" t^0,1 _зад.п (для положительной логики это отвечает положительно­му фронту, для отрицательной логики — отрицательному фронту выход­ного сигнала) определяется как интервал времени между входным и вы­ходным сигналами ЛЭ, измеренный на уровне 0,5 логического перепада входного и выходного сигналов.

Предельная рабочая частота элемента задает диапазон рабочих частот сигналов, переданных элементом без искривления так, чтобы за время одного такта в схеме успевали завершиться переходные процессы.

Частота переключения — максимальная частота, на которой в наихудших условиях гарантируется срабатывание счетного триггера, составленного из логических элементов данной серии.

Среднее время задержки увеличивается, если незадействован один из вхо­дов логического элемента, а также при отключении нагрузки на выходе логического элемента.

3. Схемотехнические и конструктивные параметры.

• Для построения разветвленных логических цепей необходимо, чтобы каждый ЛЭ владел определенной нагрузочной способностью по входу и выходу, то есть мог работать по нескольким логическим входам и одновременно руководить несколькими входами других ЛЭ. Нагрузоч­ную способность ЛЭ принято выражать коэффициентом объединения по входу и коэффициентом разветвления по выходу.
  

Коэффициент объединения по входу К_об с логического элемента — число входов логического элемента, по которым реализуется логическая функция, в том числе с учетом входов логического расширителя.

Коэффициент разветвления по выходу К_раз логического элемента — число единичных нагрузок, которые можно одновременно подклю­чить к выходу логического элемента. Единичной нагрузкой является один вход базового логического элемента данной серии. Каждый ЛЭ со стороны входа представляет собой нелинейную нагрузку, характер и значение которой определяются комбинацией и значением сигналов на других входах этого же элемента и разбросом параметров схемы ЛЭ. Следует помнить, что для ряда элементов данной серии один вход эквивалентен нескольким единичным нагрузкам.

• Количество источников питания, необходимое для работы данной се­рии логических элементов, — их номиналы, допуск на номиналы, ве­личины допустимых пульсаций.
  
• Тип корпуса (в том числе без корпуса). Габариты корпуса. Количество выводов корпуса.
  
• Интенсивность отказов логических элементов, что, как правило, указы­вается на микросхему в целом.
  

В реальной логической схеме каждый ЛЭ может быть нагружен на разное число других ЛЭ и соединен с ними линиями связи разной длины и кон­фигурации. В результате условия работы ЛЭ в разных схемах могут суще­ственным образом отличаться, что не должно приводить к нарушению их функционирования. Количество входов элементов другой серии специ­ально оговаривается.

4. Интегральные параметры
   

Интегральные параметры отображают уровень развития технологии и схемотехники, качество цифровых ИС. Основными интегральными пара­метрами ИС являются энергия переключения Р_т и уровень интеграции N.

Таблица 2.1. Степень интеграции логических цифровых микросхем
Условное обозначение	Число вентилей на кристалл	Число бит памяти на кристалл
ИС	До 10	До 102
СИС	102	103
БИС	103	104
СБИС	104	105
СБИС более высокой степени интеграции	105 – 108	106-107

Степень интеграции N логических цифровых микросхем (табл. 2.1) опре­деляется числом простейших эквивалентных ЛЭ — обычно вентилей с двумя входами — на кристалле. Иногда степень интеграции микросхем измеряют числом элементов (резисторов, транзисторов, диодов) на кри­сталле, но при этом совсем не учитывается специфика логических цифро­вых ЭС, где связи между элементами занимают существенную часть пло­щади кристалла. Функциональную сложность ИС запоминающих устройств, которые имеют регулярную структуру, можно оценивать числом бит па­мяти на коисталле.

Приложение А

СЕРИИ К155, КМ155 Тип логики: ТТЛ.

Состав серии:

К155ЛА1, КМ155ЛА1 — два элемента 4И—НЕ.

К155ЛА2, КМ155ЛА2 — элемент 8И — НЕ.

К155ЛАЗ, КМ155ЛАЗ —четыре элемента 2И—НЕ.

К155ЛА4, КМ155ЛА4 —три элемента ЗИ—НЕ.

К155ЛА6, КМ155ЛА6 —два элемента 4И—НЕ с большим коэффициентом разветвления.

К155ЛА7, КМ155ЛА7 —два элемента 4И—НЕ с открытым коллекторным выходом и

повышенной на­грузочной способностью.

К155ЛА8, КМ155ЛА8 —четыре элемента 2И—НЕ с открытым коллекторным выходом.

К155ЛР1, КМ155ЛР1 —два элемента 2—2И—2ИЛИ—НЕ (один расширяемый по ИЛИ).

К155ЛРЗ, КМ155ЛРЗ —элемент 2—2—2—ЗИ—4ИЛИ—НЕ с возможностью расширения

по ИЛИ.

К155ЛР4, КМ155ЛР4 — элемент 4-4И-2ИЛИ-НЕ с возможностью расширения по ИЛИ.

К155ЛД1, КМ155ЛД1 —два четырехвходовых расширителя по ИЛИ.

К155ЛДЗ, КМ155ЛДЗ —восьмивходовый расширитель по ИЛИ.

К155ИЕ1 —декадный счетчик с фазоимпульсным

представлением информации.

К155ИЕ2, КМ155ИЕ2 —двоично-десятичный 4-разрядный счетчик.

К155ИЕ4, КМ155ИЕ4 —счетчик-делитель на 12.

К155ИЕ5, КМ155ИЕ5 —двоичный счетчик.

К155ИЕ6, КМ155ИЕ6 —двоично-десятичный реверсивный счетчик.

К155ИЕ7, КМ155ИЕ7 —4-разрядный двоичный реверсивный счетчик.


Контрольные вопросы

1. Объясните, что такое логический элемент.
   
2. Какие виды логических операций вы знаете.
   
3. Расскажите о такой логической операции как конъюнкция.
   
4. Расскажите о такой логической операции как дизъюнкция.
   
5. Расскажите о такой логической операции как инверсия.
   
6. Что собой представляет Схемы И—НЕ, ИЛИ-НЕ.
   
7. Что такое Элемент цифрового устройства.
   
8. Что такое Элемент цифровой схемотехники.
   
9. Что такое Логический элемент.
   
10. Расскажите об общих характеристиках элементов логических устройств.
    

Лекция 5