Кр вуз фпт

Вид материала

Конспект

Содержание План лекции Форма представления Унарная — это система счисления, в которой для записи чисел используется только один знак— | В непозици­онной системе цифры не меняют своего количественного значения при изменении их расположения в числе. Основание системы счисления — количество Шестнадцатеричная система счисления Двоично-десятичная система счисления 1.5. Элементы двоичной арифметики 0110 0100 Умножение представляет собой многоразовое сложение промежуточных сумм и сдвиги. 10011 х 101

Подобный материал:

• К вопросу о создании асу вуз: Проблемы создания и внедрения, 16.08kb.
• Программа : Учебная программа имеет модульную структуру и состоит из: обязательных, 93.82kb.
• Работа выполнена в научно-исследовательском секторе Школы-студии (вуз) им. Вл. И. Немировича-Данченко, 7376.04kb.
• Д. Е. Бурланков Все физические явления разворачиваются в пространстве с течением времени:, 268kb.
• В г. Ростове-на-Дону > I. Общие положения нир является одним из основных направлений, 69.33kb.
• Преемственность в обеспечении непрерывного экономического образования в системе «школа-ссуз-вуз», 463.36kb.
• Всероссийский конкурс «директор школы 2010» Принятие управленческих решений в организации, 816.08kb.
• Сегодня дпи нгту единственный в Нижегородском регионе вуз, где готовят инженеров химического, 79.68kb.
• Instituto Superior Tecnico крупнейший, наиболее престижный инженерный вуз Португалии,, 14.38kb.
• Гневашева В. А. Российский студент: социальный облик. По материалам мониторинга «Российский, 1950.72kb.

Тема 1: Формы изображения информации


План лекции:

• Системы счисления
  
• Элементы двоичной арифметики
  

1.4. Системы счисления.

Начнем с некоторых общих замечаний относительно понятия число. Можно считать, что любое число имеет значение (содержание) и форму представления.

Значение числа задает его отношение к значениям других чисел ("больше", "меньше", "равно") и, следовательно, порядок расположения чисел на число­вой оси.

Форма представления, как следует из названия, определяет порядок записи числа с помощью предназначенных для этого знаков. При этом значе­ние числа является инвариантом, т. е. не зависит от способа его представле­ния. Это означает также, что число с одним и тем же значением может быть записано по-разному, т. е. отсутствует взаимно однозначное соответствие между представлением числа и его значением.

Способ представления числа определяется системой счисления.

Определение

Система счисления — это правило записи чисел с помощью заданного набора специальных знаков — цифр.

Людьми использовались различные способы записи чисел, которые можно объединить в несколько групп: унарная, непозиционные и позиционные.

Унарная — это система счисления, в которой для записи чисел используется только один знак— | (вертикальная черта, палочка). Следующее число полу­чается из предыдущего добавлением новой палочки: их количество (сумма) равно самому числу. Унарная система важна в теоретическом отношении, поскольку в ней число представляется наиболее простым способом и, следо­вательно, просты операции с ним. Кроме того, именно унарная система опре­деляет значение целого числа количеством содержащихся в нем единиц, ко­торое, как было сказано, не зависит от формы представления.

1. = I
   
2. = I I ;
   

5 = I I I I I;

10 = I I I I I I I I I I.

Такая система счисления является непозиционной, так как цифры не меняют своего количественного значения при изменении их расположения в числе.

Определение

В непозици­онной системе цифры не меняют своего количественного значения при изменении их расположения в числе.

Из непозиционных наиболее распространенной можно считать римскую сис­тему счисления. В ней некоторые базовые числа обозначены заглавными ла­тинскими буквами:

1 —I, 100 —С,

5 —V, 500 —D,

10 —X, 1000 —М.

50 —L,

Все другие числа строятся комбинаций базовых в соответствии со следующими правилами:

• если цифра меньшего значения стоит справа от большей цифры, то их зна­чения суммируются; если слева— то меньшее значение вычитается из большего;
  
• цифры I, X, С и М могут следовать подряд не более трех раз каждая;
  
• цифры V, L и D могут использоваться в записи числа не более одного раза.
  

Например, запись XIX соответствует числу 19, а MDXLIX— числу 1549.

Римская система счисления является смешанной, так как значе­ние каждой цифры частично зависит от ее места (позиции) в числе. Так, в числах: VII; VI; IV - V обозначает 5, а I обозначает 1. Но, с другой стороны, важно, как цифры расположены относительно друг друга:

VII = 5 + 1 + 1 = 7; VI = 5 + 1 = 6; IV = 5 - 1 = 4.

Запись чисел в такой системе громоздка и неудобна, но еще более неудобным оказывается выполнение в ней даже самых простых арифметических опера­ций. Отсутствие нуля и знаков для чисел больше М не позволяют римскими цифрами записать любое число (хотя бы натуральное). По указанным причи­нам теперь римская система используется лишь для нумерации.

В настоящее время для представления чисел применяют, в основном, позици­онные системы счисления.

Определение

Позиционными называются системы счисления, в которых значение каждой цифры в изображении числа определяется ее положением (по­зицией) в ряду других цифр.

Н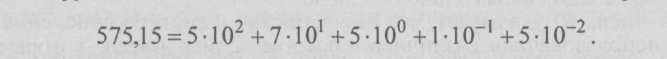аиболее распространенной и привычной является десятичная система счисления, в ко­торой для записи чисел используется 10 цифр: 0, 1,2, 3, 4, 5, 6, 7, 8 и 9. Число представляет собой краткую запись многочлена, в который входят степени некоторого другого числа — основания системы счисления. Например:


В данном числе цифра 5 встречается трижды, однако значение этих цифр различно и определяется их положением (позицией) в числе. Количество цифр для построения чисел, очевидно, равно основанию системы счисления. Также очевидно, что максимальная цифра на 1 меньше основания. Причина широкого распространения именно десятичной системы счисления понят­на — она происходит от унарной системы с пальцами рук в качестве "пало­чек".

Десятичная система счисления является позиционной, так как значение каждой цифры зависит от ее места (позиции) в числе.

Например, 23 = 2 •10 + 3;

32 = 3 •10 + 2

и 23 ≠ 32.

Определение

Основание системы счисления — количество (Р) раз­личных цифр, используемых для изображения числа в позиционной системе счисления.

Значения цифр лежат в пределах от 0 до Р- 1.

В общем случае запись любого числа N в системе счисления с основанием Р будет представлять собой ряд (многочлен) вида:

N = a_m-1 х P ^m-1+а_m-2 х P ^m-2+...+a_k x P^k +...+а₁ х Р¹+a ₀ х P⁰ +…+а_-1 х P^-1 + a_-2 х Р ^-2 +…+ а _-s х Р ^–s (4.1)

Нижние индексы определяют местоположение цифры в числе (разряд):

• положительные значения индексов — для целой части числа (т разрядов);
  

• отрицательные значения — для дробной (5 разрядов).
  

Максимальное целое число, которое может быть представлено в т разрядах:

N_max = P^m - 1

Минимальное значащее, не равное 0, число, которое можно за­писать в s разрядах дробной части:

N_min = P^-s

Имея в целой части числа m разрядов, а в дробной — s, можно записать P^{m + s} разных чисел.

Двоичная система счисления имеет основание Р = 2 и использует для представления информации две цифры: 0 и 1.

Интерес имен­но к этой системе счисления связан с тем, что, как указывалось выше, любая информация в компьютерах представляется с помощью двух состояний — 0 и 1, которые легко реализуются технически

Существуют правила перевода чисел из одной системы счисле­ния в другую, основанные, в том числе, и на выражении (4.1).

Например, двоичное число 101110,101 равно десятичному числу 46,625:

101110,101₂= 1•2⁵ + 0•2⁴+ 1•2³+ I 1 10,Ючисле, и на выражении (1ции, представление чисел в ЭВМ.•2²+ 1•2¹+0•2⁰ +1•2 ^-1+0•2^-2+1•2^-3 = 46,625₁₀.

Практически перевод из двоичной системы в десятичную мож­но легко выполнить, надписав над каждым разрядом соответствую­щий ему вес и сложив затем произведения значений соответствую­щих цифр на их веса.

Например, двоичное число 01000001₂ равно 65₁₀. Действительно, 64 • 1 + 1 • 1 = 65.

Вес	128	64	32	16	8	4	2	1
Цифра	0	1	0	0	0	0	0	1

Таким образом, для перевода числа из позиционной системы счисления с любым основанием в десятичную систему счисления можно воспользоваться выражением (4.1).

Обратный перевод из десятичной системы счисления в систему счисления с другим основанием непосредственно по (4.1) затрудни­телен, поскольку все арифметические действия, предусмотренные этой формулой, следует выполнять в той системе счисления, в кото­рую число переводится. Обратный перевод выполняется значитель­но проще, если предварительно преобразовать отдельно целую и дробную части выражения (4.1) к виду

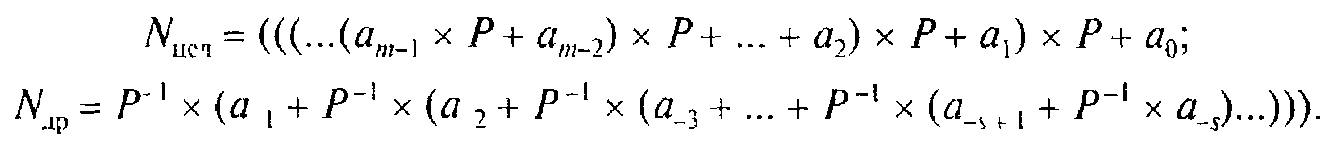4.2

Алгоритм перевода числа из десятичной системы счисления в систему счисления с основанием Р, основанный на этих выражени­ях, позволяет оперировать числами в той системе счисления, из ко­торой число переводится, и может быть сформулирован следующим образом.

1. Целочисленно разделить исходное число (Z₁₀) на основании новой системы счисления (q) и найти остаток от деления — это будет цифра 0-го разряда числа Z_q.
   
2. Частное от деления снова целочисленно разделить на q с выделением остатка; процедуру продолжать до тех нор, пока частное от деления не окажется меньше q.
   
3. Образовавшиеся остатки от деления, поставленные в порядке, обрат­ном порядку их получения, и представляют Z_q.
   

П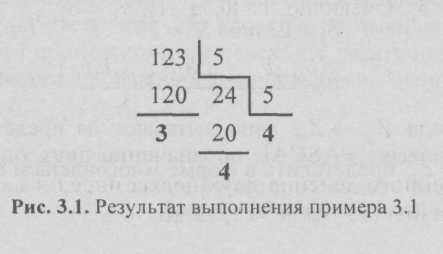ример 1 Выполнить преобразование 123₁₀ Z₅..


Z=443₅

Остатки от деления (3, 4) и результат последнего целочисленного деле­ния (4) образуют обратный порядок цифр нового числа. Следовательно, 123,0₁₀ =443₅.

Необходимо заметить, что полученное число нельзя читать как "четыре­ста сорок три", поскольку десятки, сотни, тысячи и прочие подобные обо­значения чисел относятся только к десятичной системе счисления. Про­читывать число следует простым перечислением его цифр с указанием системы счисления ("число четыре, четыре, три в пятеричной системе счисления").

Алгоритмы перевода числа из одной системы в другую явно вытекают из представлений (4.1) или (4.2): необходимо Z_р представить в форме многочлена и выполнить все опе­рации по правилам десятичной арифметики.

Пример 2 Выполнить преобразование 443₅ Z₁₀.

Решение: 443₅ =4·5²+4·5¹+3·5⁰=4·25 + 4·5 + 3·1 = 123₁₀.

Необходимо еще раз подчеркнуть, что приведенными алгоритмами удобно пользоваться при переводе числа из десятичной системы в какую-то иную или наоборот. Они работают и для перевода между любыми иными система­ми счисления, однако преобразование будет затруднено тем, что все арифме­тические операции необходимо осуществлять по правилам исходной (в пер­вых алгоритмах) или конечной (в последнем алгоритме) системы счисления.

По этой причине переход, например, Z₃Z₈ проще осуществить через промежуточное преобразование к десятичной системе Z₃ Z₁₀ Z₈. Си­туация, однако, значительно упрощается, если основания исходной и конеч­ной систем счисления оказываются связанными соотношением p = q^r, где r — целое число (естественно, большее 1).

При переводе смешанного числа следует переводить его целую и дробную части отдельно.

1. Для перевода целой части числа ее, а затем целые части полу­чающихся частных от деления, следует последовательно делить на основание Р до тех пор, пока очередная целая часть частного не окажется равной 0. Остатки от деления, записанные последователь­но справа налево, образуют целую часть числа в системе счисления с основанием Р.

2. Для перевода дробной части числа ее, а затем дробные части получающихся произведений, следует последовательно умножать на основание Р до тех пор, пока очередная дробная часть произведения не окажется равной 0 или не будет достигнута нужная точность дро­би. Целые части произведений, записанные после запятой последо­вательно слева направо, образуют дробную часть числа в системе счисления с основанием Р.

Пример 3. Пусть требуется перевести смешанное число из десятичной в двоичную систему счисления на примере числа 46,625. 46,625₁₀ Z₂..

1. Переводим целую часть числа: 46 :2 = 23 (остаток 0).

23 : 2 = 11 (остаток 1).

11:2 = 5 (остаток 1).

5:2=2 (остаток 1).

2:2=1 (остаток 0).

1 : 2 = 0 (остаток 1),

Записываем остатки последовательно справа налево — 101110, т. е. 46₁₀= 101110₂

2.. Переводим дробную часть числа: 0,625 •2 = 1,250.

0,250 •2 = 0,500.

0,500 •2 = 1,000 (дробная часть равна 0 → стоп).

3. Записываем целые части получающихся произведений после за­пятой последовательно слева направо — 0,101, т. е. 0,625₁₀ = 0,101₂.

Окончательно: 46,625₁₀= 101110,101₂.

Кроме двоичной и десятичной при работе с компьютером часто используются также восьмеричная, двоично-десятичная и шестнадцатеричная сис­темы счисления.

Однако в истории человечества имеются свидетельства использования и дру­гих систем счисления — пятеричной, шестеричной, двенадцатиричной, двад­цатиричной и даже шестидесятиричной.

Шестнадцатеричная система счисления часто используется при программировании. Перевод чисел из шестнадцатеричной системы счисления в двоичную систему весьма прост — он выполняется по­разрядно.

Для изображения цифр используются цифры и буквы: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F. где в шестнадцатеричной систе­ме счисления буквам придают значения:

А =10, В=11, С =12, D=13, Е= 14, F= 15.

Например, шестнадцатеричное число F17B в двоичной системе выглядит так: 1111000101111011, а в десятичной — 61 819.

Двоично-десятичная система счисления получила большое рас­пространение в современных компьютерах ввиду легкости перевода в десятичную систему и обратно. Она используется там, где основное внимание уделяется не простоте технического построения ма­шины, а удобству работы пользователя. В этой системе счисления все десятичные цифры отдельно кодируются четырьмя двоичными цифрами и в таком виде записываются последовательно друг за другом.

Двоично-десятичная система не экономична с точки зрения реализации технического построения машины (примерно на 20 % увеличивается требуемое оборудование), но очень удобна при под­готовке задач и при программировании. В двоично-десятичной сис­теме счисления основанием системы счисления является число 10, но каждая десятичная цифра (0, 1, ..., 9) кодируется двоичными цифрами.

Пример: десятичное число 16 в двоично-десятичной системе выглядит так: 0001 0110

Десятичный код	Двоичный код	Восьмеричный код	Шестнадцатиричный код
0	0000 0000	00	00
1	0000 0001	01	01
2	0000 0010	02	02
3	0000 0011	03	03
4	0000 0100	04	04
5	0000 0101	05	05
6	0000 0110	06	06
7	0000 0111	07	07
8	0000 1000	10	08
9	0000 1001	11	09
10	0000 1010	12	0А
11	0000 1011	13	0B
12	0000 1100	14	0C
13	0000 1101	15	0D
14	0000 1110	16	0E
15	0000 1111	17	0F

Десятичный код	Двоичный код	Восьмерич ный код	Шестнадца тиричный код
16	0001 0000	20	10
17	0001 0001	21	11
18	0001 0010	22	12
19	0001 0011	23	13
20	0001 0100	24	14
21	0001 0101	25	15
22	0001 0110	26	16
23	0001 0111	27	17
24	0001 1000	30	18
25	0001 1001	31	19
26	0001 1010	32	1A
27	0001 1011	33	1B
28	0001 1100	34	1C
29	0001 1101	35	1D
30	0001 1110	36	1E
31	0001 1111	37	1F

1.5. Элементы двоичной арифметики.

Рассмотрим, как выполняются арифметические действия в двоичной системе. Для этого проведем анализ таблиц сложения и умножения в двоичной системе:

Арифметические действия над двоичными числами выполняются соответст­венно приведенным ниже выражениям.

Сложение Вычитание Умножение

0+0=0 0-0=0 0·0=0

1+0=1 1-0=1 1·0=0

0+1=1 1-1=0 0·1=0

1+1=10 10-1=1 1(1=1)

Сложение двух многоразрядных двоичных чисел проводится поразрядно с учетом единиц переполнения от предшествующих разрядов.

1011

+ 1011

10110

Вычитание многоразрядных двоичных чисел, аналогично сложению, начина­ется из младших разрядов. Если занять единицу в старшем разряде, образу­ются две единицы в младшем разряде.

1010

- 0110

0100

Умножение представляет собой многоразовое сложение промежуточных сумм и сдвиги.

10011

х 101

10011

00000

10011

1011111


Процесс деления состоит из операций вычитания, которые повторяются. 101010 111

- 111 110

0111

- 111

0000 0000

Следует обратить внимание на аналогию в правилах выполне­ния арифметических действии в двоичной и десятичных системах счисления если при сложении двух двоичных чисел (точнее, пред­ставленных в двоичной системе счисления) сумма цифр окажется больше единицы, то возникает перенос в старший разряд, если уменьшаемая цифра меньше вычитаемой, то нужно сделать «заем» единицы в старшем разряде

Анализируя примеры умножения в двоичной системе счисле­ния, необходимо обратить внимание на одну важную особенность выполнения этой операции в данной системе. Так как очередная цифра множителя может быть только 1 или 0, то промежуточное произведение равно либо множимому, либо 0. Таким образом, опе­рация умножения в двоичной системе фактически не производится в качестве промежуточного произведения записывается либо мно­жимое, либо 0, а затем промежуточные произведения суммируются. Иначе говоря, операция умножения заменяется последовательным сложением

Как уже известно, дополнительный код используется для вычитания чисел в компьютерах и позволяет эту операцию свести к сло­жению чисел

Правила выполнения вычитания с дополнительным числом (дополнительный код) следующие. Чтобы вычесть число А из числа В, достаточно сложить В с дополнительным числом А и отбросить перенос в соседний старший разряд.

Например, чтобы вычесть 623 из 842 (842 - 623 = 219), достаточно сложить 842 с 377(1000-623), отбросив перенос, получим 219 (842+377=1219).

Таким образом, важнейшее преимущество двоичной арифмети­ки заключается в том, что она позволяет все арифметические действия свести к одному — сложению, а это значительно упрощает уст­ройство процессора ЭВМ.

Изложенные здесь основные принципы положены в основу функционирования элементов и узлов ЭВМ (триггер, сумматор, полусумматор и др.).


Контрольные вопросы

1. Какие системы счисления вы знаете.
   
2. Что такое основание системы счисления.
   
3. Расскажите о двоичной системе счисления.
   
4. Переведите число 64,544₍₁₀₎ в двоичную систему.
   
5. Какие формы представления чисел применяются в ЭВМ.
   
6. Как выполняются арифметические действия в двоичной системе.
   
7. В чем различия позиционной системы исчисления и непозиционной?
   
8. Каковы преимущества и недостатки десятичной, восьмеричной и двоич­ной систем исчисления?
   
9. Приведите правила перевода из десятичной системы исчисления в двоич­ную систему и наоборот.
   
10. Приведите правила перевода из десятичной системы исчисления в вось­меричную систему и наоборот.
    
11. Приведите правила перевода из десятичной системы исчисления в шестнадцатеричную систему и наоборот.
    
12. Запишите двоично-десятичный код числа 21₍₁₀₎.
    
13. Превратите число 247₍₁₀₎ по схеме (10) →(2) → (8) →(10).
    
14. Переведите число 32,54₍₁₀₎ в двоичную систему.
    

Лекция 3