Конспект лекций москва 2004 удк 519. 713(075)+519. 76(075) ббк 22. 18я7

Вид материала

Конспект

Содержание 10. Разрешимые и неразрешимые свойства КС-грамматик 10.1. Разрешимые свойства КС-грамматик

Подобный материал:

• Учебное пособие тверь 2008 удк 519. 876 (075. 8 + 338 (075. 8) Ббк 3817я731-1 + 450., 2962.9kb.
• Тексты лекций Москва 2008 удк 339. 9(075. 8) Ббк 65. 5я73-2, 1528.45kb.
• Программно-технический комплекс Учебное пособие Новочеркасск юргту (нпи) 2010. Удк, 3911.73kb.
• Удк 152. 27 (075. 8) + 157 (075. 8) + 152. 3 (075, 60.12kb.
• Краткий конспект лекций Кемерово 2002 удк: 744 (075), 1231.26kb.
• Методические указания по курсу Новосибирск 2004 ббк ю 937. 4 Удк 152. 26 (075), 802.63kb.
• Москва 2011 ббк 63. 3 (2)я 7 к 90 удк 947 (075) История России, 110.08kb.
• Курс лекций Гродно 2005 удк 631. 1 (075., 1193.16kb.
• Удк 070(075. 8) Ббк 76. 01я73, 5789.66kb.
• Удк 339. 9(470)(075. 8) Ббк, 7329.81kb.

10. Разрешимые и неразрешимые свойства КС-грамматик

10.1. Разрешимые свойства КС-грамматик

Теорема 13. Свойство L(G) разрешимо для КС-грамматик.

Разрешимость этого свойства обеспечивается алгоритмом исключения -правил, приведенным в разделе 9.

Теорема 14. Если G=< V_T,V_N, S, R> – КС, неукорачивающая грамматика, то язык L(G) разрешим, т.е. для любой цепочки  V_T* можно определить, L(G) или же L(G).

Доказательство.

Пусть L(G) и =n. Тогда существует вывод цепочки : S,…, , ,…, , … , , т.е. некоторая цепочка  может встретиться в выводе более одного раза. Тогда, удалив из вывода фрагмент ,…, ,получим опять вывод цепочки .

Значит, для любого слова L(G) существует его бесповторный вывод в G, т.е. вывод, в котором все цепочки различны, причем длина каждой цепочки  n. Число таких цепочек ограничено числом 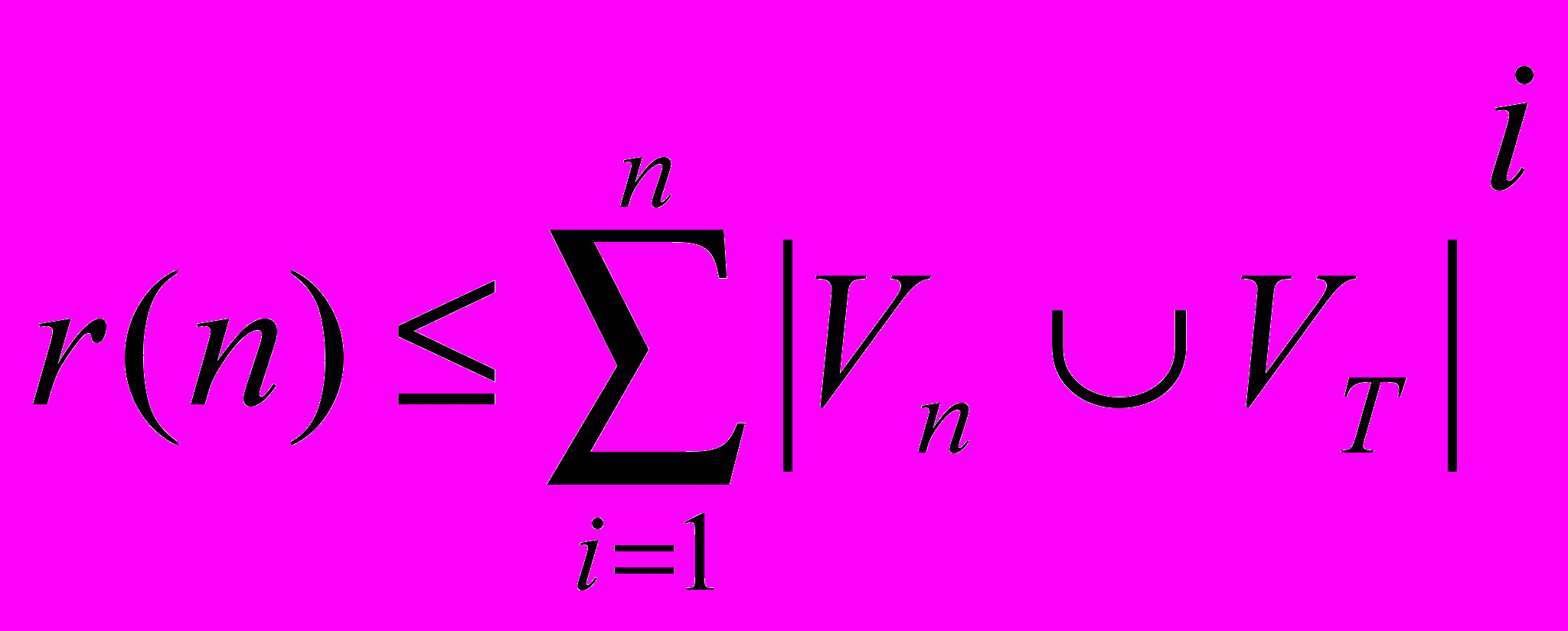, а значит, число выводов ограничена числом r(n)! (в принципе можно дать более точную оценку, но здесь достаточно и этой). Откуда получается простой алгоритм распознавания L(G) или же L(G)?

Перебираем все бесповторные последовательности цепочек длины  n , в которых каждая следующая цепочка не короче предшествующей, и проверяем, является ли она выводом в данной грамматике. Сложность такой проверки ограничена, т.к. на каждом шаге проверяем выводимость a_i+1 из a_i. Если хоть одна последовательность является выводом требуемой цепочки, то L(G), иначе L(G).

Теорема 15. Если G – приведенная грамматика без цепных правил, то существуют константы с₁ и с₂, зависящие от G, такие что для любого вывода () цепочки L(G) c₁ ()c₂, где  () – длина вывода цепочки .

Доказательство.

Пусть имеется грамматика G=< V_T,V_N, S, R>. Вводятся обозначения K – V_N, L – максимальная длина правой части правила в R, т.е. L={max A R & A V_N}. Так как G не содержит цепных и укорачивающих правил, то для любого вывода ^K , >, значит, для вывода S^K, , следовательно, ()K, с другой стороны, L(), поэтому, L (), что требовалось доказать.

Теорема 16. Если G=< V_N, V_T,S, R> – КС-грамматика, то L(G) бесконечен  существует нетерминальный символ A_i такой, что S* x A_i y, A_i⁺ z A_i w, zw 1, и A_i⁺ v, где x, y, z, w,v V_T*.

Доказательство.

Считаем, что рассматриваемая грамматика не содержит цепных правил.

1.Доказательство бесконечности языка при условии S* x A_i y, A_i⁺ z A_iw, z w 1 и A_i⁺v очевидно, так как при данных условиях фрагмент вывода A_i⁺ z A_iw может быть включен в вывод произвольное число раз; следовательно, S⁺ x v y, и S⁺ x z^j v w^jy для всех j0,что и обеспечивает построение бесконечного множества цепочек заданного вида.

2. Пусть язык, порождаемый грамматикой, является бесконечным, а условие теоремы не выполняется. Тогда максимальная глубина (длина ветви) синтаксического дерева для цепочки, порождаемой грамматикой, не превышает  V_N . Число таких деревьев конечно, значит, конечно число цепочек, порождаемых грамматикой.

Если же язык бесконечен, то глубина деревьев не ограничена, значит, в каком-нибудь синтаксическом дереве Т существует нетерминал A_i, через который ветвь дерева проходит неоднократно, причем это дерево соответствует выводу терминальной цепочки. Поэтому

во-первых, существует путь из начальной вершины в данную вершину S*  A_i, *x, *y, где x, yV_T*;

во-вторых, в силу выводимости из A_i терминальной цепочки, A_i⁺ v  vV_T*;

в третьих, из-за повторения нетерминала A_i в ветви дерева A_i⁺A_i, *z, *w, где z, w  V_T*, значит, A_i⁺ z A_iw , и вследствие отсутствия цепных правил,z w 1. Что и требовалось доказать.

Из доказанной теоремы следует

Следствие 1. Для КС-грамматики G=< V_N, V_T, S, R> существуют числа p, q, такие, что для любой цепочки L(G), если  p, то она имеет вид  =     , где  ,    q, и для любого n цепочка вида ⁿⁿ L(G), n0.

Следствие 2. Язык {aⁿ bⁿ cⁿ, n} не порождается КС-грамматикой.

Теорема 17. Свойство L(G)= разрешимо для КС-грамматик.

Разрешимость свойства следует из рассмотренных ранее алгоритмов: Язык L(G) не пуст тогда и только тогда, когда начальный символ грамматики является производящим.