Geum.ru

Конспект лекций москва 2004 удк 519. 713(075)+519. 76(075) ббк 22. 18я7

Вид материалаКонспект

Содержание


10.2. Неразрешимые свойства КС-грамматик
11. Синтаксический анализ для КС-языков
Подобный материал:
1   ...   11   12   13   14   15   16   17   18   ...   21

10.2. Неразрешимые свойства КС-грамматик


Поскольку класс множеств (слов), порождаемых грамматиками, совпадает с классом перечислимых множеств, то для языков класса «0» справедлив аналог теоремы Райса «никакое нетривиальное свойство языков класса 0 не является алгоритмически разрешимым» (т.е. для нетривиального свойства не существует алгоритма, который бы по произвольной грамматике G выяснял, обладает ли данным свойством язык L(G)).

Для КЗ-грамматик проблемы пустоты и бесконечности неразрешимы. Для КС-грамматик эти проблемы разрешимы.

Неразрешимые проблемы для КС-грамматик следуют из неразрешимости проблемы Поста.

Формулировка этой проблемы в виде, удобном для наших целей, следующая: для двух списков цепочек X=(1, 2,…, m) и Y=(1, 2,…, m) в алфавите U определить, существует ли последовательность индексов i1, i2,…, in, такая, что выполняется .

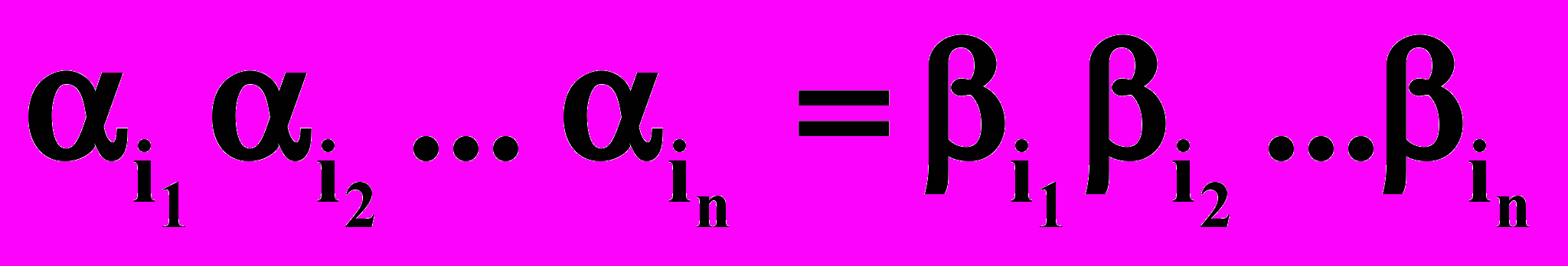Пусть U и m фиксированы. Введём алфавит дополнительных символов U0={b1,b2,…bm}, U0  U=,

U1= U0 U. Пусть X=(1, 2,…, m) – цепочки в U. Тогда Q(X) – множество цепочек вида 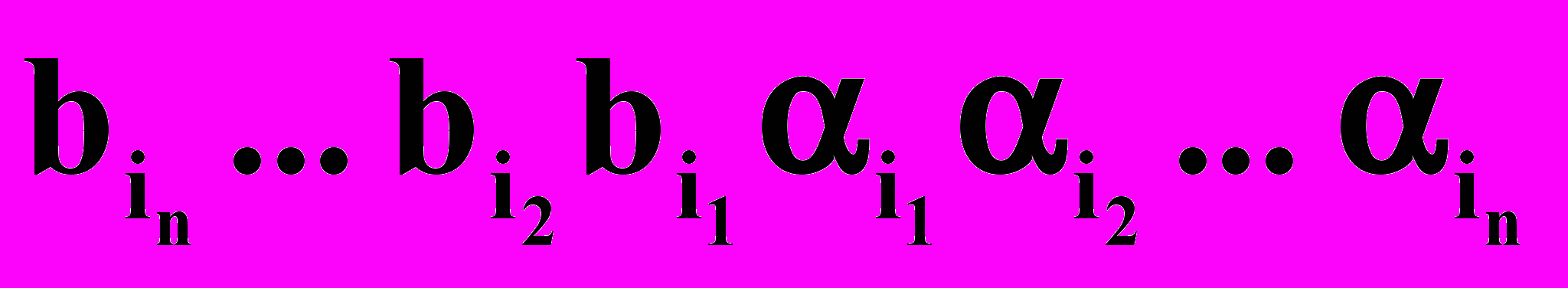, n1.

Тогда для Q(X) справедливы утверждения:

1. Если X=(1, 2,…, m) и Y=(1, 2,…, m) – списки цепочек в U, то комбинаторная проблема Поста разрешима тогда и только тогда, когда разрешимо свойство Q(X)  Q(Y) =. Пусть существует  Q(X) и Q(Y). Тогда 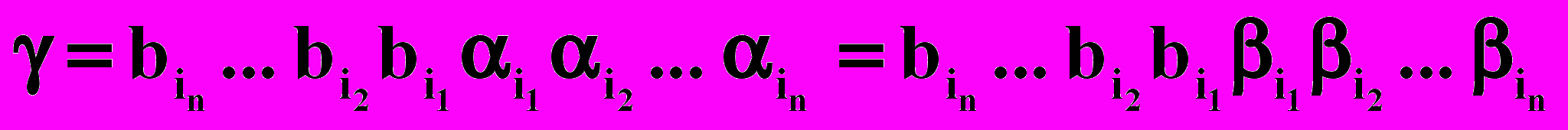, а значит, .

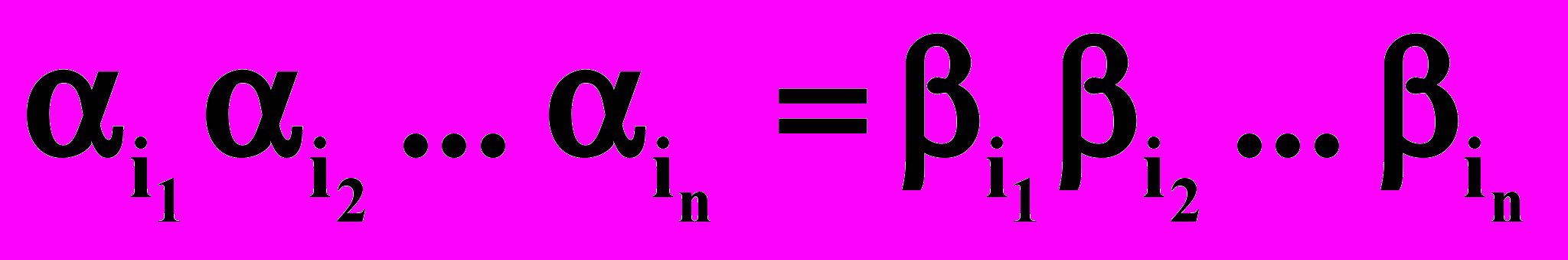2. Для любого списка X=(1, 2,…, m) цепочек в U, Q(X) – КС-язык в U1. Соответствующая КС-грамматика G=< VN, VT,S, R> для языка Q(X) – G=< {I} , U1, I, R>; R = { Ibi I i, Ibi i }. Грамматика является однозначной.

Из введенных утверждений следует теорема:

Теорема 18. Не существует алгоритма, который по двум КС-грамматикам G1 и G2 определял бы L(G1) L(G2)=?

Доказательство.

Если бы такой алгоритм существовал, то проблема Поста была бы разрешима.

Теорема 19. Не существует алгоритма, который по любой КС-грамматике позволял бы определить, является ли эта грамматика однозначной.

Доказательство.

Рассмотрим множества Q(X) для X=(1, 2,…, m) и Q(Y) для Y=(1, 2,…, m). Правила грамматики для порождения Q(X): RX={Abi A i, Abi i } правила грамматики для построения множества Q(Y): RY={ Bbi B i, Bbi i }.

Грамматика для порождения Q(X)Q(Y) G=<{A,B},U, I, R>, где R=RXRY {IAB}. Эта грамматика однозначна, если Q(X)Q(Y)=, а это свойство неразрешимо.

Другие неразрешимые проблемы для КС-языков:
  1. Является ли КС-языком пересечение КС-языка?
  2. Является ли КС-языком дополнение КС-языков?
  3. Проблема тривиальности КС-языка L=V*(= проблеме пустоты дополнения)?
  4. Проблема эквивалентности КС-грамматик.

11. Синтаксический анализ для КС-языков


Синтаксический анализ может рассматриваться в широком или же узком смысле. Синтаксический анализ в узком смысле – по цепочке определить её структуру (или же построить синтаксическое дерево), то есть задача сводится к построению вывода данной цепочки в данной грамматике.

Синтаксический анализ в широком смысле – определение, можно ли данную цепочку построить с использованием данной грамматики. Это в общем случае гораздо более сложная задача.

Существующие алгоритмы синтаксического анализа классифицируются по способу:
  1. построения вывода (нисходящие, восходящие, смешанные);
  2. выбора альтернативы (детерминированные и недетерминированные). В первом случае на каждом шаге выбирается правильная альтернатива, во втором – альтернатива выбирается наугад;
  3. возврата (для недетерминированного выбора альтернативы) – разбор с быстрым или медленным возвратом, а так же
  4. степени доступности цепочки: или цепочка доступна вся сразу, или же читается слева направо посимвольно (при этом доступно для анализа определенное число символов).

Обычно рассматривается нисходящий или восходящий разбор при чтении цепочки слева направо.