Краткий конспект лекций Кемерово 2002 удк: 744 (075)
| Вид материала | Конспект |
- Конспект лекций (для студентов всех форм обучения) Кемерово 2002, 1424.32kb.
- Конспект лекций москва 2004 удк 519. 713(075)+519. 76(075) ббк 22. 18я7, 1805.53kb.
- Конспект лекций по курсу "Начертательная геометрия и инженерная графика" Кемерово 2002, 786.75kb.
- Конспект лекций для студентов ссузов Кемерово 2010, 1664.44kb.
- Конспект лекций Для студентов вузов Кемерово 2006, 1068.06kb.
- Конспект лекций Омск 2002 удк 629. 424., 467.89kb.
- Конспект лекций кемерово 2003 удк: 637. 992, 1167.63kb.
- Конспект лекций Кемерово 2004 удк: 637. 992, 2553.59kb.
- Н. В. Рудаков Краткий курс лекций, 1552.23kb.
- Учебное пособие Кемерово 2004 удк: 637. 5: 579. 2 (075., 1001.84kb.
Министерство образования Российской Федерации
Кемеровский технологический институт пищевой
промышленности
Л.В. Громова, Л.М. Лазарева, Г.М. Мяленко,
Л.П. Козлова, Е.В. Скрынник
НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ
Краткий конспект лекций
Кемерово 2002
УДК:744 (075)
Печатается по решению Редакционно - издательского совета
Кемеровского технологического института пищевой промышленности
Рецензенты:
• доцент, зав. кафедрой прикладной механики Кемеровского
сельскохозяйственного института к.т.н. В.М. Радченко;
• доцент кафедры начертательной геометрии и графики
Кузбасского государственного университета
к.т.н. Т.А. Баздерова
Начертательная геометрия: краткий конспект лекций по курсу НГ и ИГ
Л.В. Громова, Л.П. Козлова, Л.М. Лазарева, Г.М. Мяленко, Е.В. Скрынник.
Кемеровский технологический институт пищевой промышленности. Кемерово. 2002. - 136с.
ISBN 5 - 89289 - 084 - 8
Курс лекций предназначен для студентов технологических специальностей дневной и заочной форм обучения.
В разработанном курсе лекций рассмотрены основные разделы курса "Начертательная геометрия". Лекции включают в себя сведения о методах проецирования, о образовании проекций точки, прямой линии, плоскости и их взаимном положении. Рассмотрены способы преобразования чертежа, построение многогранников и кривых поверхностей, пересечение кривых и гранных поверхностей прямой линией и плоскостью, Даны сведения об аксонометрических проекциях.
Краткий конспект лекций содержит 168 ил. и 17 библ. назв.
Н
^ ISBBN 5 - 89289 - 084 – 8
©Кемеровский технологический институт пищевой промышленности, 2002
3
ВВЕДЕНИЕ
В число дисциплин, составляющих основу инженерного образования, входит начертательная геометрия. Некоторые идеи начертательной геометрии были разработаны еще в 1б-17в.в., но в самостоятельную науку начертательная геометрия оформилась в конце 18в, в связи с возросшими потребностями инженерной практики.
^В 1798 году французский инженер Гаспар Монж опубликовал свой труд, «Начертательная геометрия» который лег в основу проекционного черчения.
В российских учебных заведениях систематическое преподавание начертательной геометрии началось с 1810 года, вначале на французском, а затем и на русском языке, В 1821 году профессор Я,С. Севастьянов издает курс «Основания начертательной геометрии».
В 1855 году профессором А.Х.Ребером написана книга по теории проекции с числовыми отметками.
Выдающийся вклад в теорию геометрии внесли русские математики Н И.Лобачевский (1792-1856 г.г.) и Л.Л.Чебышев (1821-1894 г.г,). В дальнейшем развитие начертательной геометрии как науки и учебной дисциплины; принадлежит многим советским ученым и педагогам.
Предмет изучения начертательной геометрии - разработка методов построения и чтения чертежей, а также методов решения на чертежах геометрических задач, связанных с оригиналом.
Правила построения изображений, излагаемых в начертательной геометрии, основаны на методе проекции.
^ УСЛОВНЫЕ ОБОЗНАЧЕНИЯ И СИМВОЛИКА
Для краткой записи геометрических предложений, алгоритмов решения задач и т.д. используется геометрический язык. 1. Точки обозначаются заглавными латинскими буквами:
A,B,C,D…
арабскими цифрами: 1, 2, 3,4…
последовательность точек: A1, A2, Аз.
2
4
. Линии, произвольно расположенные по отношению к плоскостям проекции, обозначаются строчными буквами латинского алфавита: а, Ь, с, d...
3. Углы - строчными буквами греческого алфавита: ф, ц, р, .
4. Плоскости - строчными буквами греческого алфавита:.
5. Поверхности - прописными буквами русского алфавита:
цилиндр - Ц, конус - К...
6. Плоскости проекций
горизонтальная - Н, фронтальная - V, профильная - W,
7. Возможное обозначение плоскостей проекций - строчной буквой греческого алфавита -; горизонтальная - 1, фронтальная - 2. профильная - 3.
8. Оси проекций - строчными буквами:
о- начало координат;
х- ось абсцисс;
у- ось ординат;
z- ось аппликат.
9. Проекции точек:
на горизонтальную плоскость Н- А', В', С',
на фронтальную плоскость V- А", В", С"...
на профильную плоскость W- А///, В///, С///...
10. Проекции линий - по проекциям точек, определяющих линию;кроме того, горизонталь- h; фронталь- f; профильная линия- р.
Символика
е - принадлежит (2N) два принадлежит N
- - включает, содержит (а - а) прямая а принадлежит плоскости
- объединение множеств |АВ| ВС| - ломаная АВС
- пересечение множеств
=>• импликация - логическое следствие (а // с и b // с) => а // Ь- [если
а // b и b // с, то а // b]
~- подобие
=- совпадают
|| - параллельны
- перпендикулярны
- - скрещиваются
—>•- преобразуется: aa1
5
^ 1. ВИДЫ ПРОЕЦИРОВАНИЯ
Существует несколько видов проецирования.
Проекции центральные, - когда задается плоскость про-екции и центр проекции точки, не лежащей в этой плоскости(рис. 1.1).
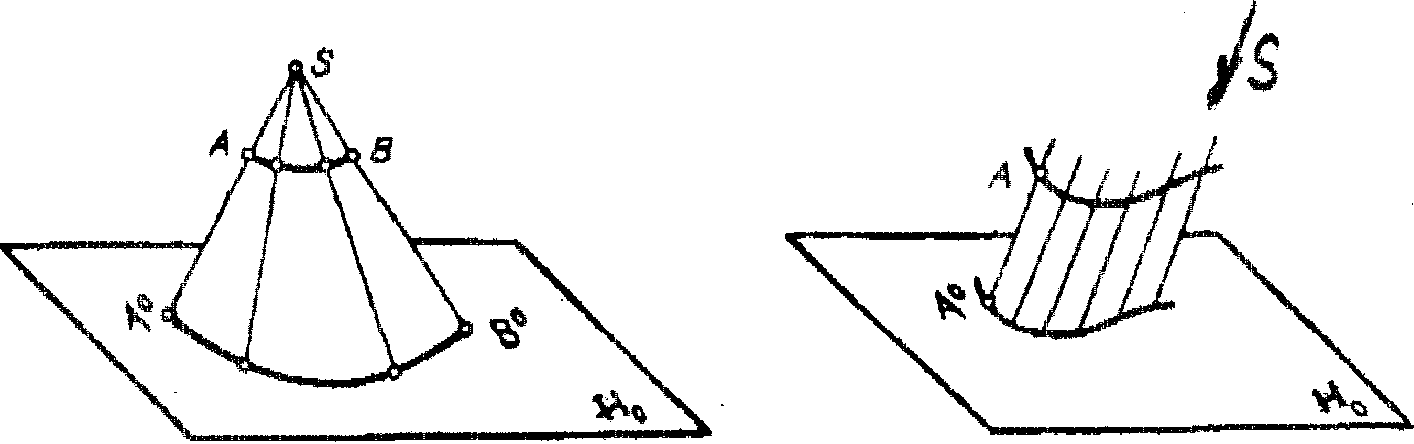
Рис. 1.1 Рис. 1.2
^ 1.1. Параллельное проецирование
Параллельной проекцией точки будем называть точку пересечения проецирующей прямой, проведенной параллельно заданному направлению, с плоскостью проекции (рис. 1.2).
Параллельные проекции также называют цилиндрическими, которые в свою очередь делятся на: косоугольные и прямоугольные.
В параллельных проекциях, так же как и в центральных:
1) для прямой линии проецирующей поверхностью в общем случаеслужит плоскость, и поэтому прямая линия вообще проецируется в виде прямой;
2) каждая точка и линия в пространстве имеют единственную своюпроекцию;
3) каждая точка на плоскости проекций может быть проекцией множества точек, если через них проходит общая для них проецирующая прямая;
4) каждая линия на плоскости проекций может быть проекцией множества линий, если они расположены в общей для них проеци-рующей плоскости;
6
5) для построения проекции прямой достаточно спроецировать две ее точки и через полученные проекции этих точек провести прямую линию,
6) если точка прямой, то проекция точки принадлежит проекции этой прямой; (рис. 1.3) точка К принадлежит прямой (проекция К0 принадлежит проекции этой прямой),
7) если прямая (АВ) параллельна направлению проецирования, то проекцией прямой является точка А°, она же В° (рис. 1.3),
8) отрезок прямой линии, параллельной плоскости проекций, проецируется на эту плоскость в натуральную величину (CD = C°D° , как отрезки параллельных прямых между параллельными прямыми), (рис. 1.3).

Рис. 1.3
В данном курсе преимущественно рассматриваются прямоугольные проекции (слово прямоугольные часто заменяют на ортогональные, образованное от греческих слов прямой и угол).
^ Точка.
Точка относится к основным неопределяемым понятиям геометрии. Точка не имеет размеров; это основной геометрический элемент линии и поверхности.
Положение точки (и любой геометрической фигуры) в пространстве может быть определено, если будет задана координатная система отнесения. Наиболее удобная является декартовая система координат (французский философ, математик Декарт 1596 - 1650 г.) состоящая из трех взаимно перпендикулярных плоскостей, при этом получается восемь октантов (рис. 1.4).
7

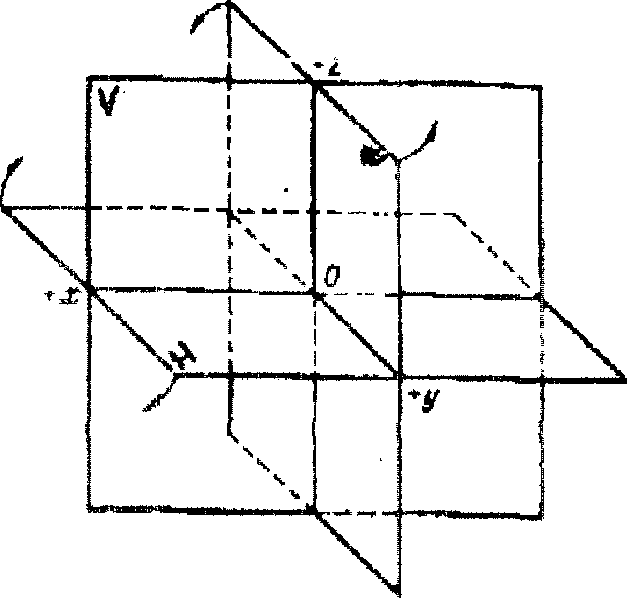
Рис. 1.4
Рис. 1.5
Преобразование в эпюр осуществляется совмещением плоскостей путем вращения (рис. 1.5), Или условно можно принять для построения одну из четвертей.
Рассмотрим принятую систему расположения плоскостей проекций (рис. 1.6).
Условимся называть: плоскость - Н- горизонтальная плоскость проекции, V- фронтальная плоскость проекции, W-профильная плоскость проекции.
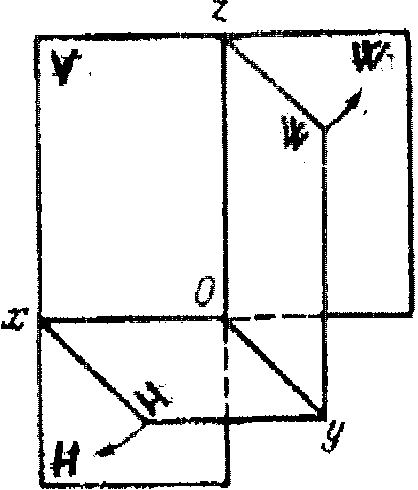

Рис. 1.6
^ 1.3. Проецирование точки на две плоскости проекции
Возьмем точку А и поместим в пространство двухгранного угла, образованного двумя перпендикулярными плоскостями: фронтальной- V и горизонтальной- Н (рис. 1.7).
8
Ф
 ронтальная плоскость V изображена в виде прямоугольни-ка, а плоскость Н- горизонтальная плоскость в виде параллело-грамма,, Наклонная сторона обычно проведена под углом 45° к горизонтали.
ронтальная плоскость V изображена в виде прямоугольни-ка, а плоскость Н- горизонтальная плоскость в виде параллело-грамма,, Наклонная сторона обычно проведена под углом 45° к горизонтали.Рис. 1.7
Из точки А опускаем перпендикуляр на плоскости [АА'; АА" - проецирующие лучи].
Точки А', А" (рис. 1.7) пересечений с плоскостями проекций V и Н являются прямоугольными проекциями точки А, а полученная фигура в пространстве АА' АхА" - прямоугольник.
Если совместим плоскость Н с плоскостью V путем вращения вокруг линии пересечения плоскостей X, то получается комплексный (плоский) чертеж (эпюр Монжа) точки А.
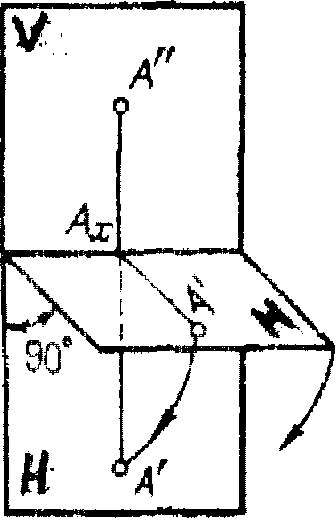
Рис. 1.8
9
Для упрощения комплексного чертежа границы плоскостей не указываются. Линия пересечения плоскостей V фронтали и Н горизонтали называют осью проекции (рис, 1.9),
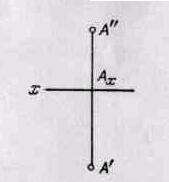
Рис. 1.9
Перпендикуляры, проведенные из точки А к плоскостям проекций, называются проецирующими линиями, а основания этих проецирующих линий точки А' и А"' - называются проекциямиточки А. А - горизонтальная проекция точки А и А"- фронтальная проекция точки А.
^ 1.4. Расположение точек на комплексном чертеже
Расположение проекции точки на комплексном чертеже
зависит от положения точки в пространстве (рис. 1.10).
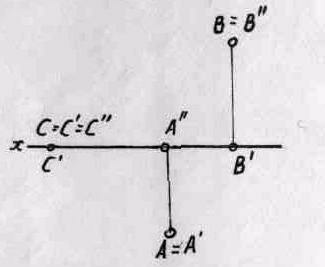
Рис. 1.10
10
Если точка А — лежит на плоскости Н, то ее горизонтальная проекция совпадает с точкой А, а фронтальная с осью х.
Соответственно точка В лежит на V плоскости, то ее фрон-тальная проекция совпадает с точкой В, а горизонтальная лежит на оси х , Если точка С лежит на оси х, то проекции С', С" сов-падают с точкой С.
^ 1.5.Проецирование точки на три плоскости проекции
В тех случаях, когда по двум проекциям нельзя представить форму предмета, его проецируют на три плоскости (рис. 1.11), т.е. вводится W- профильная плоскость, она перпендикулярна двум имеющимся, (Н и V).
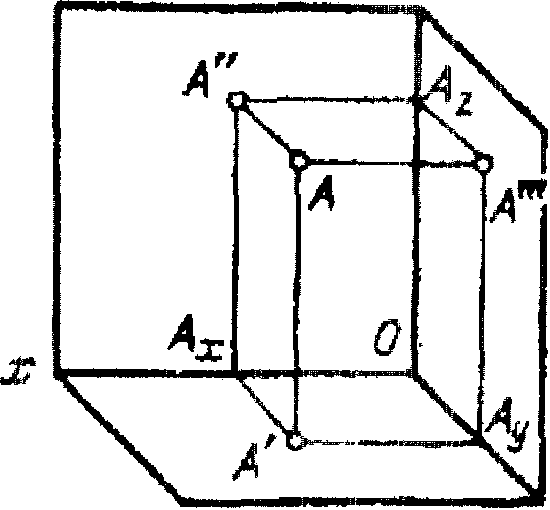
Рис. 1.11
Для получения комплексного чертежа точки А вращаем плоскости вокруг осей х; z. Он будет выглядеть следующим об- разом, Расстояние (координата) точки А до плоскости Н будет равна ОАх.
Координата точки А до V равна ОАу. Координата точки А до W равна OAz. А=х,у; А" = x.z; А / = y,z.
По двум проекциям точки, находящихся в проекционной связи, можно определить все три координаты точки.
11
Если заданы координаты точки А (ха, ya, 2.л) то можно по-строить три проекции этой точки. На рис. 1,12 представлен ком-плексный чертёж точки А к рис. 1.11,
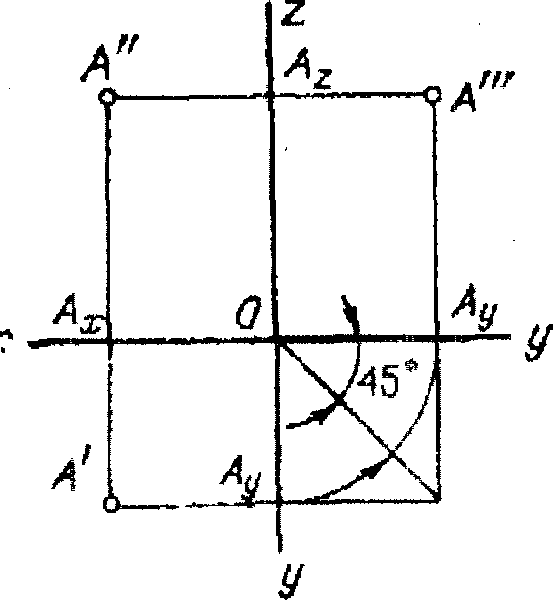
Рис. 1.12
^ 2. ПРОЕЦИРОВАНИЕ ОТРЕЗКА ПРЯМОЙ ЛИНИИ
2.1 Проецирование прямой линии на две и три плоскости проекции.
Прямая линия в пространстве вполне определяется положением двух любых точек, принадлежащих этой прямой (траектория перемещения точки), рис. 2.1.
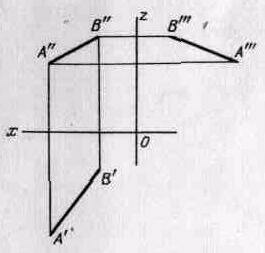
Рис. 2.1 Рис. 2.2
12
При проецировании прямой линии проецирующие лучи всех
точек прямой располагаются в одной плоскости, которую назы-вают проецирующей. Эта плоскость пересекает плоскость про-екции по прямой линии.
Для того, чтобы построить эпюр прямой линии, достаточнодостроить проекции двух лежащих на ней точек и провести че-
рез соответствующие проекции точек проекции прямой.
^ Если прямая не перпендикулярная, и не параллельная ни од-ной из плоскостей проекции, то такая прямая называется,прямой общего положения (рис.2.2),
В дальнейшем мы будем изображать пересечение коорди-натных плоскостей только осями.
^ 2.2.Положение прямой линии относительно плоскостипроекции
Если прямая в пространстве параллельна какой - либо плоскости проекции, то такая прямая называется прямой частного положения.
Прямая линия может занимать относительно плоскостей проекций особые (частные) положения. Рассмотрим их по сле-дующим двум признакам;
1.Прямая параллельна одной плоскости проекции (прямые уровня рис.2.3, 2.4, 2.5).
2.Прямая параллельна двум плоскостям проекции (проецирую-щие прямые рис.2.6, 2.7, 2.8).
Прямая параллельная горизонтальной тоскости проекции (Н), называется горизонталью и обозначается h (рис.2.3.), (z-const).

Рис.2.3
13
Особенности горизонтали: все точки горизонтали удалены на одинаковое расстояние от плоскости Н.
Фронтальная проекция прямой параллельна оси проекции и горизонтальная проекция отрезка этой прямой равна самому отрезку А'В' = АВ – (натуральная величина), А»В'' параллельна оси х А»'В'» параллельна оси у.
