Конспект лекций москва 2004 удк 519. 713(075)+519. 76(075) ббк 22. 18я7

Вид материала

Конспект

Содержание 7.3. Расширенная форма Бекуса – Наура (РБНФ) Идентификатор = буква  буква цифра. 7.4. Синтаксическая диаграмма 8. Структура цепочек. СУ-схемы G. Пусть дана грамматика G L называется неоднозначным, если для него не существует однозначной грамматики. Например, L={a

Подобный материал:

• Учебное пособие тверь 2008 удк 519. 876 (075. 8 + 338 (075. 8) Ббк 3817я731-1 + 450., 2962.9kb.
• Тексты лекций Москва 2008 удк 339. 9(075. 8) Ббк 65. 5я73-2, 1528.45kb.
• Программно-технический комплекс Учебное пособие Новочеркасск юргту (нпи) 2010. Удк, 3911.73kb.
• Удк 152. 27 (075. 8) + 157 (075. 8) + 152. 3 (075, 60.12kb.
• Краткий конспект лекций Кемерово 2002 удк: 744 (075), 1231.26kb.
• Методические указания по курсу Новосибирск 2004 ббк ю 937. 4 Удк 152. 26 (075), 802.63kb.
• Москва 2011 ббк 63. 3 (2)я 7 к 90 удк 947 (075) История России, 110.08kb.
• Курс лекций Гродно 2005 удк 631. 1 (075., 1193.16kb.
• Удк 070(075. 8) Ббк 76. 01я73, 5789.66kb.
• Удк 339. 9(470)(075. 8) Ббк, 7329.81kb.

7.3. Расширенная форма Бекуса – Наура (РБНФ)

Часто применяется так называемая расширенная БНФ – РБНФ, в которой используются метасимволы (,); [,]; {,}. Введение метасимволов позволяет сделать запись более лаконичной. Синтаксис РБНФ следующий:

1. Нетерминалы записываются как последовательность символов.
   
2. Терминалы (последовательности символов) заключаются в кавычки.
   
3. Знак  , используемый в математической записи грамматик, обозначается как =.
   
4. Альтернативы, как и в математической записи грамматик, разделяются знаком .
   
5. Конструкция, заключенная в  ,  , является необязательной.
   
6. Конструкция, заключенная в  , , может повторяться произвольное число раз, от 0 (эквивалент * в регулярных выражениях).
   
7. ( ) служат для факторизации, т.е. конструкция  может быть представлена в виде (). Это позволяет использовать конструкцию выбора на более глубоком уровне.
   
8. В конце каждого описания ставится точка.
   

Например, идентификатор в РБНФ можно описать так:

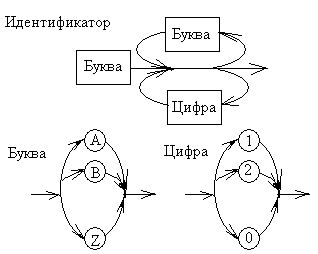
Идентификатор = буква  буква цифра.

буква = 'А’ | ‘В’ | ‘С’ |….| ‘Z’.

цифра = ‘0’ | ‘1’ | ... | ‘9’.

Существительное описывается как

существительное = основа ( окончание единственного числа окончание множественного числа).

Фактически, в правой части правил в РБНФ записывается некоторое регулярное выражение, в котором могут использоваться нетерминалы (т.е. расширение возможностей относительно выразительной мощности обычных регулярных выражений, т.к. обычные регулярные выражения позволяют описывать А-языки, а РБНФ – КС-языки).

7.4. Синтаксическая диаграмма

Синтаксическая диаграмма – графическая форма представления РБНФ. Для каждого нетерминала рисуется своя диаграмма. Приняты следующие обозначения:

1. Нетерминалы заключаются в прямоугольники.
   
2. Терминалы заключаются в овалы.
   
3. Образы нетерминалов и терминалов соединяются линиями (со стрелками или без них, далее используются стрелки для указания направления движения) так, чтобы множество путей соответствовало множеству цепочек из терминалов и нетерминалов, задаваемому правилами РБНФ, для которых строится диаграмма.
   

Диаграммы для конструкции выбора и итерации представлены на рис. 18, а и б, соответственно. Скругленный прямоугольник может быть заменен как прямоугольником (в случае нетерминала), так и овалом ( в случае терминала). Набор диаграмм для идентификатора приведён на рис.19.



Рис.18

В большинстве случаев существует не единственная форма представления для одних и тех же объектов.





Р


ис.19

Легко показать, что выразительная мощность РБНФ и БНФ совпадает:

Условная запись РБНФ	Условная запись БНФ для данной РБНФ
А= (12).	<А> ::=<>< 1>< ><2>
А= [ ] .	<А> ::=<>< >< >
А= { } .	<А> ::= <> ::= <> < B>

8. Структура цепочек. СУ-схемы

Цепочка – последовательность лексем(терминалов). Структура цепочки – способ задания семантики (смысла) правильной последовательности лексем (т.е. принадлежащей формальному языку).

Структура может выражать непосредственно семантические связи слов (для естественного языка) или, например, порядок вычислений (для арифметических выражений), вложенность конструкций (для языков программирования).

Например, для цепочки ad2+c структура (рис.20) будет выражать порядок действий (знак  использован для обозначения возведения в степень).



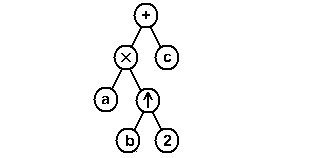
Рис.20

Структура этой же цепочки может быть представлена также в виде скобочной записи: (( (a)  ( (d)(2)) )+ (c) ).

Обычной задачей является определение структуры цепочки, построенной в некоторой конкретной грамматике G.

Пусть дана грамматика G₁₃ с множеством правил:

S T + ST

T M  T  M

M (S)  i

ализируемая цепочка x = i + i  i. Для неё можно построить несколько выводов, различающихся порядком замены нетерминалов, например: S  T +S  T + T  T+ M  TT + M  M   M + M  M i + M  Mi + M  ii + i  i , или S T +S  M + S  i + Ti + M  T i + i  T i + i  Mi + i  i.

Легко заметить, что по существу эти выводы различаются незначительно. Для придания единообразия процессу построения вывода определим: вывод, в котором на каждом шаге правило применяется к самому правому (левому) нетерминалу, называется правым (левым) выводом. Второй из приведенных выводов для цепочки i + i  i является левым выводом, т.к. на каждом шаге правило применяется к самому левому нетерминалу.

Одна из форм представления вывода – синтаксические дерево.

Правила построения синтаксического дерева.

1. Каждому правилу вывода A₁₂…_nR, где _i – некоторые лексемы, сопоставляется куст.
   

	A
1	2	…	n

2. Строим дерево с корнем, растущее вниз. Корню дерева приписываем начальный символ.
   
3. Для каждого применяемого правила в выводе приклеиваем соответствующий куст к вершине построенного дерева.
   
4. Повторяем шаг 3 до тех пор, пока всем висячим вершинам будут сопоставлены терминалы.
   

Для грамматики G₁₃ кусты, соответствующие правилам грамматики, приведены на рис. 21,а; синтаксическое дерево для цепочки i + i  i в этой грамматики представлено на рис. 21,б.

Теорема 12. Каждому выводу некоторой терминальной цепочки соответствует единственное синтаксическое дерево. Каждому синтаксическому дереву соответствует единственный правый (левый) вывод.

Доказательство.

1. Для построенного вывода дерево единственно по построению.
   
2. Пусть для данной цепочки имеется некоторое синтаксическое дерево. Построим левый вывод, соответствующий этому дереву. Для этого в дереве на каждом шаге применяем соответствующее правило к самому левому нетерминалу. Предположим, что одному дереву соответствует более одного правого (левого) вывода. Если существует 2 вывода, соответствующих этому дереву, то существует нетерминал, к которому применяются разные правила, следовательно, соответствующие деревья будут различными. Поэтому каждому дереву соответствует единственный правый (левый) вывод.
   

Соответствие дерево – вывод не является взаимно-однозначным, т.к. порядок применения правил не задан и одному дереву может соответствовать более одного вывода, например, правый и левый.

Цепочка xL(G) называется неоднозначной в G, если для неё существует более одного синтаксического дерева в G. Грамматика G называется неоднозначной, если L(G) содержит неоднозначные в G цепочки.

а)

б)

Рис.21

Язык L называется неоднозначным, если для него не существует однозначной грамматики.

Например, L={aⁿbⁿc^m, aⁿb^mc^m , n,m 1} – неоднозначный язык в классе КС-грамматик.

Регулярные выражения всегда задают однозначный язык: можно построить детерминированный автомат, и каждой цепочке (однозначному проходу по диаграмме) соответствует единственное синтаксическое дерево, т.к. этот проход задаёт однозначный порядок применения правил.

Неоднозначные грамматики часто проще однозначных, но они пригодны только для построения цепочек, а не для их анализа, т.е. задания семантики.

Для задания структуры цепочек часто используются СУ-схемы, т.е. схемы синтаксически управляемого перевода.

СУ- схема T=< V_вх,V_вых, V_N, I, R>, где V_вх – входной алфавит , V_вых – выходной алфавит , V_N – множество нетерминалов, I – начальный нетерминал, R={ A₁,₂}, где A V_N, ₁(V_вх V_N)*, ₂(V_вых V_N)*, а «,» – метасимвол, разделяющий ₁ и ₂. При этом количество и состав нетерминалов в ₁ и ₂ совпадают. Если в ₁ более одного вхождения некоторого нетерминала А, то устанавливается соответствие между всеми вхождениями А в ₁ и ₂: А⁽¹⁾, А⁽²⁾…А⁽ⁿ⁾.

СУ-схема называется простой, если порядок вхождений нетерминалов в ₁ совпадают с порядком вхождений нетерминалов в ₂.

Вывод в СУ-схеме строится из пары начальных символов . Определение выводимости в СУ-схеме подобно определению выводимости (выводимость за один шаг обозначаем )для обычных грамматик:

₁₁ ₂₂ (из ₁₁ непосредственно выводима ₂₂)  ₁₁ А ₂, ₂₁ ₁ ₂ ₁=₁ А ₂, ₂ =₁ ₂ ₂, и А₁,₂ R, при этом вхождения А в ₁ и ₁ –соответствующие.

Выводимость является рефлексивным и транзитивным замыканием непосредственной выводимости.

Применение СУ-схемы к цепочке состоит в том, из пары начальных символов по правилам схемы строится вывод таким образом, чтобы до запятой получилась исходная цепочка, в этом случае после запятой получается перевод этой цепочки.

Перевод, порождаемый СУ-схемой Т:

(T) = {/ ⁺ & xV_вх*, yV_вых*}.

Из СУ-схемы T можно извлечь две грамматики G_вх=< V_N,V_вх, I, R_вх>, где R_вх={A ₁/ A₁,₂ R} и G_вых=< V_N, V_вых, I, R_вых>, где R_вых={A ₂/ A₁,₂ R}.

СУ-схемы позволяют задавать структуры на уровне описания языка, где (T) = {/ x – входная цепочка, y – выходная цепочка}.

Например, СУ-схема Т, описывающая перевод арифметического выражения, составленного с использованием символов сложения, умножения и скобок, в скобочную запись, отражающую порядок построения формулы (а следовательно, и порядок проведения вычислений), выглядит следующим образом.


S T+S, (T+S);

S T,T;

TMT, (MT);

TM, M;

M (S), (S);

M i, ( i ).

Применение данной СУ- схемы к цепочке i+ii проиллюстрируем выводом (приводится левый вывод):

   

 < i + T, ( ( i ) + T) >  < i + M  T , ( ( i ) + ( M  T ) ) >   < i + i  T, ( ( i ) + ( ( i )  T ) )>  < i+ i  M, ( ( i ) + ((i)M))> 

 < i + i  i , ( ( i ) + ( ( i )  ( i ) ) ) >

В результате получается перевод цепочки, отражающий порядок её построения.

Можно построить СУ-схему для других преобразований цепочки, например, для построения по цепочке её польской записи. СУ-схема для построения прямой польской записи для цепочек, использующих только знаки умножения и сложения, выглядит следующим образом:

S T+S, +TS;

S T, T;

T MT, MT;

T M, M;

M (S), S;

M i, i.

Применение этой схемы к цепочке i+ii:

<Т+S,+TS>  .

Следует обратить внимание, что в обоих случаях применяемые СУ-схемы были простыми.