Конспект лекций москва 2004 удк 519. 713(075)+519. 76(075) ббк 22. 18я7

Вид материала

Содержание

6.5. Минимизация числа состояний автомата
Минимизация автоматов по методу Хафмена
Минимизация не полностью определенных автоматов

Подобный материал:

1 ... 4 5 6 7 8 9 10 11 ... 21

6.5. Минимизация числа состояний автомата

Минимизация автоматов методом таблиц различий

Алгоритм основан на анализе языка L, порождаемого (или распознаваемого) автоматом.

Идея: разбить множество состояний на непересекающиеся множества неразличимых состояний (т.е. состояний, порождающих или распознающих одинаковые множества строк).

Строятся матрицы D₀, D₁,… , указывающие различимость состояний по строкам длины n. Состояния q_i и q_j различимы по строке длины 0 (T на пересечении строки i и столбца j матрицы D₀): q_i D₀ q_j (q_iK) & ( q_j K)  (q_i K)&( q_jK).

Различимость для строк ненулевой длины определяется по индукции: при i > 0 состояния q_k и q_j различимы по строке длины i, т.е. (q_k D_i q_j )  q_k D_i_-1 q_j или aV_T, такой, что F(q_k,a) D_i_-1 F(q_j,a).

Состояние q_k различимо от состояния q_j , если  i 0 , такое, что q_k D_i q_j .

Очевидно, что q_k D_i q_j  существует строка x, x i , что (F(q_k, x)K ) & ( F(q_j, x) K)  (F(q_k, x) K) & (F(q_j, , x)K).

Если же состояния неразличимы, то их можно объединить в одно состояние; получившийся автомат будет эквивалентен исходному.

Пример. Рассмотрим автомат S_C, диаграмма которого представлена на рис. 14.

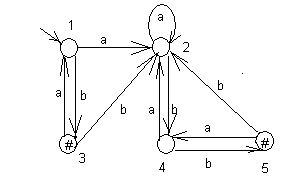
Рис.14

Матрицы, получающиеся при анализе автомата:

D₀

F T F T

T F T

T F

T

D₁

T T F T

T T T

T F

T

D₂=D₁

Из анализа полученной матрицы получаем три класса эквивалентных состояний:

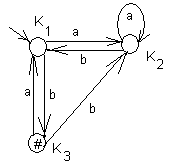
Рис.15

K₁ = {1, 4}, K₂ = {2}, K₃ = {3,5}. Диаграмма автомата, получающегося при объединении эквивалентных состояний автомата S_C, представлена на рис. 15.

Минимизация автоматов по методу Хафмена

Этот метод применим как для лингвистических автоматов, так и для автоматов Мили (для них метод описан в разделе 12).

Идея: объединение в один класс предположительно эквивалентных состояний, а затем проверка, являются ли состояния действительно эквивалентными (неразличимыми). Затем, если состояния неэквивалентны, классы разбиваем на подклассы, и проверка повторяется. Если состояния ведут себя одинаково, то процедура закончена, и получившиеся классы являются состояниями минимизированного автомата.

Алгоритм минимизации лингвистического автомата методом Хафмена.

Составляем таблицы переходов и выходов. По строкам указываются входы, по столбцам – состояния, в которые автомат переходит при данном входе.
Составляем классы предположительно эквивалентных состояний. В этом случае начальное разбиение происходит на класс конечных состояний и тех состояний, которые не являются конечными.
Составляем таблицу переходов, где в ячейках вместо состояний указываются классы, которым принадлежат эти состояния. Затем анализируем полученную таблицу: если в пределах одного класса состояния ведут себя по-разному, то класс разбивается на соответствующие подклассы, и возвращаемся к шагу 3.
Если во всех классах состояния ведут себя одинаково, то это действительно классы эквивалентности, и процедура закончена.

Строится автомат, состояниями которого являются классы эквивалентности исходного автомата.

Применение метода к автомату, диаграмма которого представлена на рис. 14, имеющему таблицу переходов

	1	2	3	4	5
a	2	2	1	2	4
b	3	4	2	5	2

и конечные состояния 3, 5, на первом шаге дает классы К₁= {3, 5}, K₂= {1, 2, 4} и, соответственно, получаем таблицу переходов (для наглядности в таблицу добавлена строка, с указанием номера класса, которому принадлежит состояние):

№ класса	2	2	1	2	1
Вход\состояние	1	2	3	4	5
a	K₂	K₂	K₂	K₂	K₂
b	К₁	K₂	K₂	К₁	K₂

Видно, что класс K₂разбивается на два класса K₃= {1, 4}, K₄={2}. Получается таблица переходов:

№ класса	3	4	1	3	1
Вход\состояние	1	2	3	4	5
a	K₄	K₄	K₃	K₄	K₃
b	К₁	K₃	K₄	К₁	K₄

Состояния в классах оказываются эквивалентными. Очевидно, что, как и следовало ожидать, получившийся минимальный автомат совпадает с тем, который получен методом таблиц различий.

Диаграмма полученного автомата приведена на рис. 15.

Минимизация не полностью определенных автоматов

(на примере лингвистического автомата, диаграмма которого представлена на рис. 13).

При минимизации не полностью определенных лингвистических автоматов начальное разбиение множества состояний делается так же, как для полностью определённого автомата: на конечные и неконечные состояния. Для данного случая классы K₁={B, C, F} – конечные состояния, K₂= {A, D, E, G} – неконечные. Приведем таблицы переходов состояний для этого автомата.

Исходная таблица:

	A	B	C	D	E	F	G
a	C	B	B	F	-	F	F
b	E	E	G	E	-	E	E
c	-	-	-	-	D	-	D

Проставляем классы состояний (в дополнительной верхней строке указываем номер класса состояния):

№	2	1	1	2	2	1	2
	A	B	C	D	E	F	G
a	K₁	K₁	K₁	K₁	-	K₁	K₁
b	K₂	K₂	K₂	K₂	-	K₂	K₂
c	-	-	-	-	K₂	-	K₂

Далее разбиваем классы на подклассы в соответствии с одинаковостью и различием столбцов. Класс K₂ разбивается на 3 класса K₃ = {A, D}, K₄= {E}, K₅ = {G}.

№	3	1	1	3	4	1	5
	A	B	C	D	E	F	G
a	K₁	K₁	K₁	K₁	-	K₁	K₁
b	K₄	K₄	K₅	K₄	-	K₄	K₄
c	-	-	-	-	K₃	-	K₃

Получившаяся таблица показывает, что класс K₁ также разбивается на два класса K₆= {B, F}, K₇= {C}.

№	3	6	7	3	4	6	5
	A	B	C	D	E	F	G
a	K₇	K₆	K₆	K₆	-	K₆	K₆
b	K₄	K₄	K₅	K₄	-	K₄	K₄
c	-	-	-	-	K₃	-	K₃

И, наконец, разбивается класс K₃: K₈= {A}, K₉={D}.

№	8	6	7	9	4	6	5
	A	B	C	D	E	F	G
a	K₇	K₆	K₆	K₆	-	K₆	K₆
b	K₄	K₄	K₅	K₄	-	K₄	K₄
c	-	-	-	-	K₉	-	K₉

Это разбиение не приводит в дальнейшему разбиению классов и получившиеся классы состояний автомата являются классами эквивалентности, а автомат, состояниями которого являются классы эквивалентности исходного автомата, – минимальный. 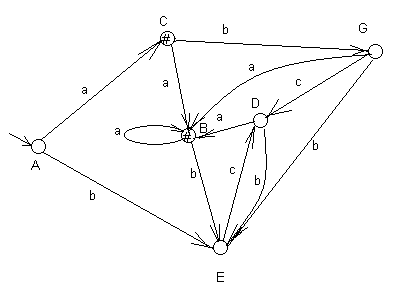Диаграмма минимизированного автомата S_B’, на которой все классы, кроме 6-го, поименованы единственным входящим в них состоянием, а класс K₆– символом B, представлена на рис. 16.