Конспект лекций москва 2004 удк 519. 713(075)+519. 76(075) ббк 22. 18я7

Вид материала

Конспект

Содержание 6.7. Разрешимые проблемы для А-грамматик 7. Нотации для задания КС-грамматик 7.1. Математическая нотация 7.2. Бекусова нормальная форма

Подобный материал:

• Учебное пособие тверь 2008 удк 519. 876 (075. 8 + 338 (075. 8) Ббк 3817я731-1 + 450., 2962.9kb.
• Тексты лекций Москва 2008 удк 339. 9(075. 8) Ббк 65. 5я73-2, 1528.45kb.
• Программно-технический комплекс Учебное пособие Новочеркасск юргту (нпи) 2010. Удк, 3911.73kb.
• Удк 152. 27 (075. 8) + 157 (075. 8) + 152. 3 (075, 60.12kb.
• Краткий конспект лекций Кемерово 2002 удк: 744 (075), 1231.26kb.
• Методические указания по курсу Новосибирск 2004 ббк ю 937. 4 Удк 152. 26 (075), 802.63kb.
• Москва 2011 ббк 63. 3 (2)я 7 к 90 удк 947 (075) История России, 110.08kb.
• Курс лекций Гродно 2005 удк 631. 1 (075., 1193.16kb.
• Удк 070(075. 8) Ббк 76. 01я73, 5789.66kb.
• Удк 339. 9(470)(075. 8) Ббк, 7329.81kb.

6.7. Разрешимые проблемы для А-грамматик

Теорема 8 .Если L – А-язык, и ZL имеет длину  числа состояний детерминированного автомата, то Z=WXY, гдеX1 и W Xⁱ Y L для всех i0.

Доказательство.

Пусть есть некоторый А-язык и автомат M_L, порождающий этот язык.

Q={ q₀,_.q₁,q₂,…,q_n-1} – множество состояний автомата M_L , n – число состояний автомата, q₀ – начальное состояние автомата.

F(q₀,Z)K т.к. ZL. Zn , поэтому q_jQ , что Z=WXY, X 1, F(q₀,W)= q_j, F(q_j,X )= q_j, F(q_j, Y)K. Но тогда F(q₀,W XⁱY)K для всех i0, что требовалось доказать.

Теорема 9. Проблема непустоты для А-грамматик разрешима, т.е., если задана А-грамматика G, то существует алгоритм, позволяющий ответить на вопрос: L(G)= ?

Доказательство.

Например, по предыдущей теореме, если L(G), то существует цепочка длины меньшей n, где n – число состояний детерминированного автомата, и перебирая все цепочки длины , не превосходящей n, можно определить, принадлежит ли какая-нибудь из них языку, порождаемому автоматом(хотя это и не оптимальное решение).

Теорема 10. Проблема равносильности А-грамматик разрешима. т.е., если G₁ и G₂ – А-грамматики, то существует алгоритм, позволяющий определить, L(G₁)=L(G₂)?

Доказательство.

В случае равенства языков минимизированные детерминированные автоматы, построенные по этим грамматикам, будут совпадать с точностью до обозначений состояний.

Теорема 11. Проблема конечности языка, порождаемого А-грамматикой, разрешима.

Доказательство.

Обозначим множество состояний, достижимых из состояния A_i , как H(A_i). Тогда, если  A_i, такое, что A_i H(q₀ )& A_i H(A_i)& A_j  H(A_i )& A_jK, то язык, порождаемый автоматом, бесконечен.

Интересно отметить, что подобная теорема существует и для КС-грамматик.

7. Нотации для задания КС-грамматик

7.1. Математическая нотация

Математическая нотация (которую рассматривали до сих пор) – чисто синтаксическое задание.

7.2. Бекусова нормальная форма

БНФ (Бекусова нормальная форма, или форма Бекуса — Наура) есть способ записи грамматики, который широко используется для описания синтаксиса языков программирования. В БНФ:

1. Нетерминальные символы записываются как имена, заключенные в угловые скобки < > .
   
2. Знак  записывается как :: = (читается "заменяется на").
   
3. Альтернативы замены, соответствующие одному и тому же нетерминалу в левой части, отделяются друг от друга вертикальной чертой  (читается "или").
   
4.  не обозначается, для того чтобы не пропустить эту альтернативу, она обычно записывается первой в конструкции выбора.
   

Используя БНФ описание идентификатора как произвольной последовательности букв и цифр, начинающейся с буквы, можно, например, записать:

<идентификатор> ::= <буква> | <буква> <продолжение>

<продолжение> ::= < символ> | < символ> <продолжение>

<символ> ::= < буква> | <цифра>

<буква> :: = А | В | С|….| Z

<цифра> ::= 0 | 1 | ... | 9

Или:

<идентификатор> ::= <буква> <продолжение>

<продолжение> ::= | < символ> <продолжение>

<символ> ::= < буква> | <цифра>

<буква> :: = А | В | С|….| Z

<цифра> ::= 0 | 1 | ... | 9

При записи в виде грамматики G₁₂ семантику увидеть сложнее (запись полностью соответствует последнему варианту БНФ):

S 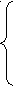 S₁ S₂ ,

S₂  S₃ S₂  ,

S₃  S₁ S₄ ,

S₁  А | В | С| … | Z ,

S₄  0 | 1 | ... | 9 .

Нетерминал БНФ может интерпретироваться как язык, который порождается грамматикой, в которой данный символ является начальным символом грамматики. БНФ может использоваться для описания синтаксиса любого языка, не только искусственного, например:

<Существительное > :: =<основа > <окончание>

<окончание > ::= окончание множественного числа окончание единственного числа…

Или:

формула исчисления высказываний::= элементарная формула(формула исчисления высказыванийбинарная операция формула исчисления высказываний) (отрицание формула исчисления высказываний)

элементарная формула::= константа пропозициональная переменная

константа::= 01

пропозициональная переменная ::=ab…z

отрицание::= N

бинарная операция ::= 