Конспект лекций москва 2004 удк 519. 713(075)+519. 76(075) ббк 22. 18я7

Вид материала

Конспект

Содержание 2. Языки. Операции над языками 2.1. Теоретико-множественные операции 2.2.Специфические операции V* (алфавит можно рассматривать как язык, состоящий из односимвольных слов) образует язык, состоящий из всех возможных цепочек, 3. Абстрактные формальные системы Каноническая система А существует каноническая система над А

Подобный материал:

• Учебное пособие тверь 2008 удк 519. 876 (075. 8 + 338 (075. 8) Ббк 3817я731-1 + 450., 2962.9kb.
• Тексты лекций Москва 2008 удк 339. 9(075. 8) Ббк 65. 5я73-2, 1528.45kb.
• Программно-технический комплекс Учебное пособие Новочеркасск юргту (нпи) 2010. Удк, 3911.73kb.
• Удк 152. 27 (075. 8) + 157 (075. 8) + 152. 3 (075, 60.12kb.
• Краткий конспект лекций Кемерово 2002 удк: 744 (075), 1231.26kb.
• Методические указания по курсу Новосибирск 2004 ббк ю 937. 4 Удк 152. 26 (075), 802.63kb.
• Москва 2011 ббк 63. 3 (2)я 7 к 90 удк 947 (075) История России, 110.08kb.
• Курс лекций Гродно 2005 удк 631. 1 (075., 1193.16kb.
• Удк 070(075. 8) Ббк 76. 01я73, 5789.66kb.
• Удк 339. 9(470)(075. 8) Ббк, 7329.81kb.

2. Языки. Операции над языками

Произвольное множество цепочек над алфавитом V, иначе любое подмножество свободной полугруппы V*, называется фомальным языком над V. Поэтому язык может быть задан как любое множество:

• перечислением элементов;
  
• ограничивающим свойством;
  
• через известные множества;
  
• порождающей процедурой.
  

В основном будем использовать четвёртый способ, но рассмотрение языков начнем с третьего способа их представления.

Например, для любого V множество слов четной длины является языком. Множество слов нечетной длины также является языком, но в отличие от первого — не замкнутым относительно операции конкатенации. Будем обозначать языки буквой L (с индексами или без них). Рассмотрим операции над языками.

Так как язык является множеством, то применимы все соответствующие операции, для которых выполняются все законы теории множеств.

В частности,  L,  L.

2.1. Теоретико-множественные операции

Пусть L₁ и L₂ – два языка над алфавитом V. Язык L называется объединением этих языков ( обозначается L = L₁  L₂ ), если L ={x / x L₁  x L₂}.

Пересечением языков L₁ и L₂ называется язык L (обозначается L = L₁ L₂ ), такой, что L ={x / x L₁ & x L₂}.

Дополнением языка L₁ до V* называется язык L (обозначается L=V*\L₁), такой, что L={ x/ xV* & x L₁}.

2.2.Специфические операции

Произведением (иначе конкатенацией) языков L₁ и L₂ называется язык L (обозначается L=L₁L₂), если L={x y/xL₁ & yL₂}.

Например, L₁={ ac, a }, L₂={ cb, b}, тогда L₁L₂ ={ acb, accb, ab}.

Свойства операции конкатенации:

1. операция умножения языков ассоциативна:
   

L₁ (L₂ L₃)= (L₁ L₂) L₃;

2. операция умножения языков дистрибутивна относительно объединения:
   

L (L₁L₂ ) = LL₁  LL₂ ,

(L₁L₂ ) L = L₁L  L₂L;

3. операция умножения языков не коммутативна: L₁ L₂ L₂ L₁.
   
4. L {}= {} L = L;
   
5. L(L₁L₂ )  LL₁  LL₂ , в общем случае равенства нет, что легко показать, подобрав соответствующий пример.
   

В силу ассоциативности операции произведения, как и в случае конкатенации цепочек, 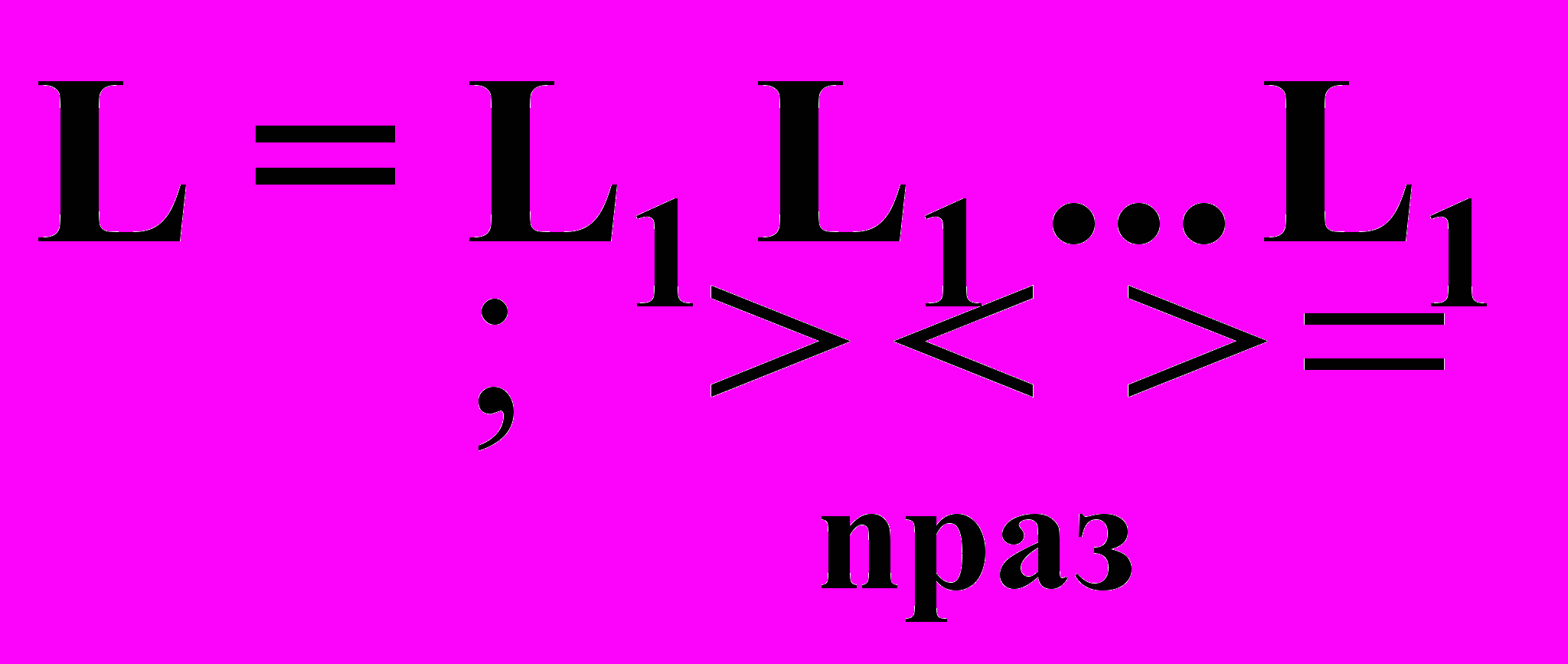записывается как L=L₁ⁿ. По определению, L⁰={}. Отметим, что {}   . так как  (пустой язык) вообще не содержит никаких цепочек.

Итерацией языка L₁ называется язык L (обозначается L=L₁*), если L=L₁⁰  L₁¹  L₁² 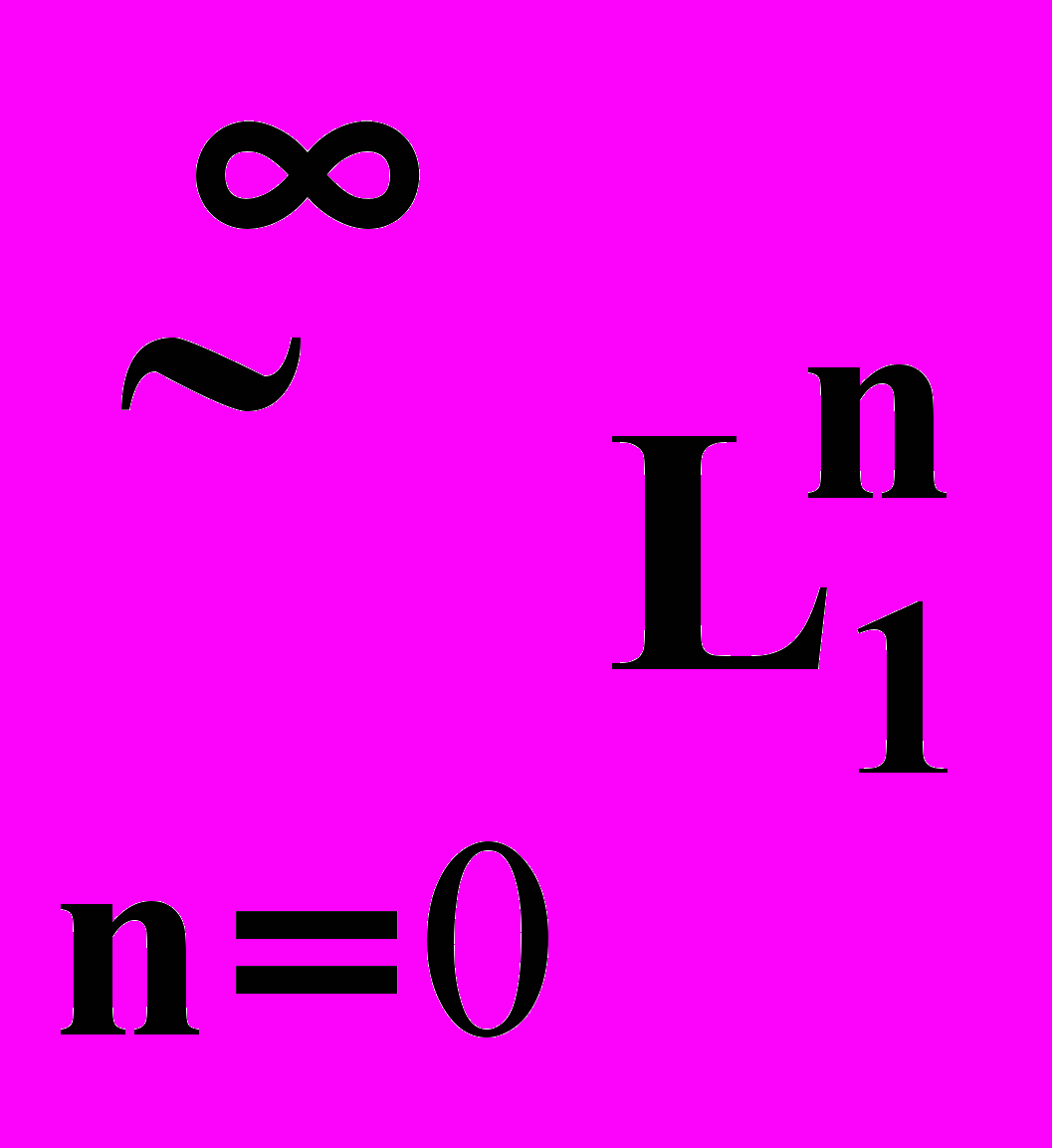… =. Как нетрудно видеть, итерация алфавита V* (алфавит можно рассматривать как язык, состоящий из односимвольных слов) образует язык, состоящий из всех возможных цепочек, составленных из символов V. Это обстоятельство и объясняет, почему V* используется для обозначения всех слов над алфавитом V.

Вводится также операция усеченной итерации. L называется усеченной итерацией языка L₁ (обозначается L=L₁⁺), если L=L₁⁰  L₁¹  L₁² … =.

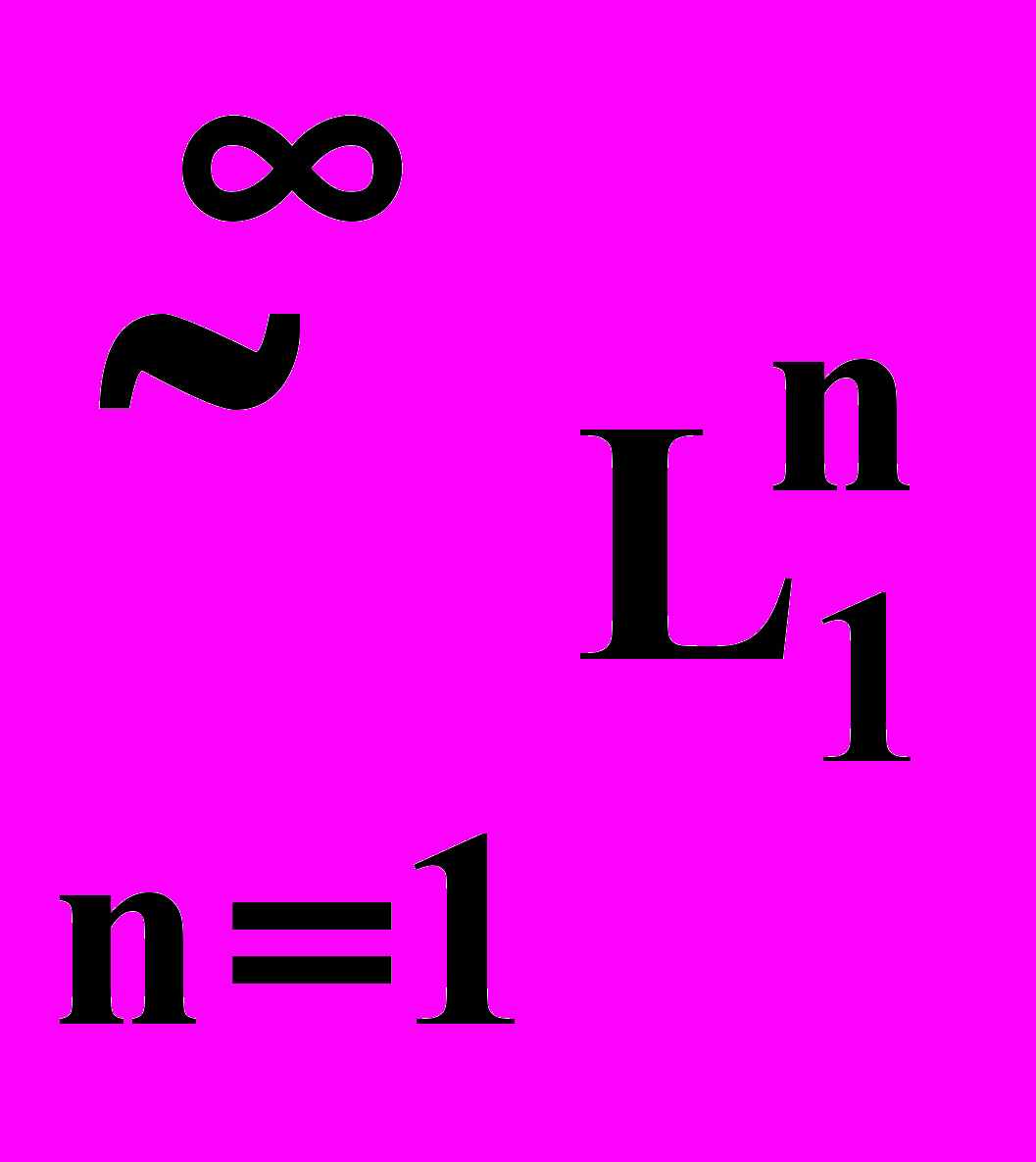3. Абстрактные формальные системы

Абстрактная формальная система – это

1. Алфавит А ( множество слов в этом алфавите – А*).
   
2. Разрешимое множество А₁  А*, элементы множества А₁ называют аксиомами.
   
3. Конечное множество вычислимых отношений R_i (₁, …, _n, ) на множестве A*, называемых правилами вывода. В этом случае слово  непосредственно выводимо из слов ₁, …, _n по правилу R_i.
   

Аксиомы тоже могут быть заданы как унарные отношения, но это не всегда удобно.

Выводимость. Вывод формулы В из формул A₁, A₂, … , A_n – последовательность формул F₁, F₂, … , F_m = B, такая, что F_i (i=1,…, m) – либо аксиома, либо одна из формул A₁, A₂, … , A_n, либо непосредственно выводима из некоторого подмножества множества {F₁, F₂, … , F_i-1}по одному из правил вывода. Если существует вывод формулы В из формул A₁, A₂, … , A_n, то В выводима из A₁, A₂, … , A_n . Множество формул, выводимых из аксиом, называется теоремами теории.

Теорема 1. Для любой формальной теории множество выводимых в ней слов перечислимо.

Доказательство.

Рассмотрим А** – множество всех конечных последовательностей ₁, …, _n, где _i – слова в алфавите А. А** – перечислимо. Из-за разрешимости множества аксиом и вычислимости правил вывода по любой последовательности можно эффективно узнать, является ли она выводом в данной формальной системе (FS).

Если в процессе перечисления А** отбрасывать все последовательности, не являющиеся выводами, то получаем перечисление множества выводов, а значит, последних слов выводов.

Следовательно, множество слов (формул), выводимых в произвольной формальной системе, перечислимо.

Примеры формальных систем: системы продукций Поста (канонические системы), системы подстановок, формальные грамматики, исчисления и т.д.

Каноническая система – это , где

A= {a₁,a₂,…, a_n} – алфавит констант,

X= {x₁, x₂,…,x_m} – алфавит переменных,

M= {M₁, M₂, …, M_k} – множество аксиом, M_i(AX)*,

R = {R₁, R₂, …, R_l} – множество продукций, имеющих вид ₁, ₂,…, _j, где _i, (AX)*, ₁, ₂,…,_j называются посылками,  – следствием (заключением).

Слова в (AX)* называются термами, слова в А* – просто словами.

Слово  называется применением аксиомы , если  получается из  подстановкой слов вместо переменных.

Слово  непосредственно выводимо из ₁, …, _n применением продукции R , если существует подстановка слов вместо переменных в продукцию R, которая посылки превратит в ₁, …, _n, а заключение – в .

Например, из acab , cabb применением продукции a x₁ b, x₁ b x₂  b x₂ (подстановка x₁=ca, x₂=b) непосредственно выводимо bb.

Выводимость – транзитивное и рефлексивное замыкание непосредственной выводимости.

Доказуемое в формальной системе утверждение (теорема формальной системы) – утверждение, выводимое из множества аксиом.

Например, формальная система <{I}, {x}, {I}, {xx I I}> позволяет построить множество нечетных чисел в унарном представлении.

Теорема 2. Для любого перечислимого множества М слов в алфавите А существует каноническая система над А, множество теорем которой совпадает с М (доказательство с использованием машин Тьюринга приводится в [3]).