Конспект лекций москва 2004 удк 519. 713(075)+519. 76(075) ббк 22. 18я7

Вид материала

Конспект

Содержание 9.3. Устранение -правил Алгоритм преобразования грамматики. 9.4. Устранение цепных правил (правил вида А  В) Алгоритм исключения цепных правил.

Подобный материал:

• Учебное пособие тверь 2008 удк 519. 876 (075. 8 + 338 (075. 8) Ббк 3817я731-1 + 450., 2962.9kb.
• Тексты лекций Москва 2008 удк 339. 9(075. 8) Ббк 65. 5я73-2, 1528.45kb.
• Программно-технический комплекс Учебное пособие Новочеркасск юргту (нпи) 2010. Удк, 3911.73kb.
• Удк 152. 27 (075. 8) + 157 (075. 8) + 152. 3 (075, 60.12kb.
• Краткий конспект лекций Кемерово 2002 удк: 744 (075), 1231.26kb.
• Методические указания по курсу Новосибирск 2004 ббк ю 937. 4 Удк 152. 26 (075), 802.63kb.
• Москва 2011 ббк 63. 3 (2)я 7 к 90 удк 947 (075) История России, 110.08kb.
• Курс лекций Гродно 2005 удк 631. 1 (075., 1193.16kb.
• Удк 070(075. 8) Ббк 76. 01я73, 5789.66kb.
• Удк 339. 9(470)(075. 8) Ббк, 7329.81kb.

9.3. Устранение -правил

Устранение -правил связано с исключением построения цепочек, которые после преобразований превращаются в пустую цепочку. Цель такого преобразования грамматики – если в грамматике строится пустая цепочка, то она строится в результате первого шага построения. Применение любого из оставшихся правил приводит к построению непустых цепочек, более того, цепочка, получающаяся из каждого нетерминала, состоит не менее чем из одного терминального символа.

Алгоритм преобразования грамматики.

Пусть дана грамматика G=< V_N, V_T, S, R>, строится эквивалентная грамматика G’ =< V_N’, V_T, S, R’>.

1. Построение множества N_ = { A / A ⁺  } – множества нетерминальных символов, из которых возможен вывод пустой цепочки. Множество N_ строится итерационно.
   
   1. На первом шаге строится N_⁰:
      

N_⁰ = { B / B    R}

2. Последовательно строятся множества
   

N_ⁱ⁺¹ = N_ⁱ { B / B    R &   ( N_ⁱ)* }.

1. Построение продолжается до тех пор, пока не получим N_ⁱ⁺¹ = = N_ⁱ, тогда N_ = N_ⁱ.
   
1. Построение R’ — множества правил эквивалентной грамматики:
   
   1. если A₀ B₁ ₁ B₂ ... B_k _k  R , k  0 и B_i  N_ для 0  i  k, но ни один символ в цепочках _j, 1  j  k не содержит символа из N_, то включить в R’ все правила вида A  ₀ X₁ ₁ X₂ ... X_k_k, где X_i — либо B_i, либо  (при этом правило A   не включать; это соответствует случаю, когда все _i =  );
      
   2. если S  N_, включить в R’ также правило S’ S, где S’ – новый начальный символ.
      

Таким образом, любая КС-грамматика может быть приведена к виду, когда R либо не содержит -правил, либо есть точно одно правило S’   и S’ не встречается в правых частях остальных правил из R.

Например, пусть дана грамматика G₁₆ с множеством правил

S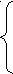A B BC;

A aAb  ;

B dBc ;

C CCAc . Строим N_⁰= {A, C}, N_¹= {A, C}= N_. Поскольку L(G) (т.к. S N_), правила грамматики примут вид


S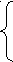A B B BC;

A aAb ab;

B dBc;

C CCAc c .

9.4. Устранение цепных правил (правил вида А  В)

Применение цепных правил приводит к увеличению длины ветвей синтаксического дерева, исключение цепных правил часто приводит к большей «прозрачности» грамматики и уменьшению длины выводов, которые можно построить.

Алгоритм исключения цепных правил.

Пусть дана грамматика G=< V_N, V_T, S, R>, строится эквивалентная грамматика G’ =< V_N’, V_T, S, R’> без цепных правил.

1. Построение для каждого A V_N множества N_A = { B / A  B }, т.е. множества нетерминальных символов, выводимых из данного символа. Итерационная процедура построения N_A:
   
   1. Начальное значение N_A⁰ ={A}.
      
   2. N_Aⁱ⁺¹ = N_Aⁱ { C / B  C  R & B  N_Aⁱ }.
      
   3. Построение продолжается до тех пор, пока не получим N_Aⁱ⁺¹ = N_Aⁱ, тогда N_A = N_Aⁱ
      
2. Построение множества R’ (множества правил эквивалентной грамматики): если B    R и не является цепным правилом, то включить в R’ все правила вида A  , для всех таких A, что B  N_A.
   

Рассмотрим пример. Пусть множество правил грамматики G₁₇ имеет вид:

ST+ST;

T MTM;

M (S) i .

Построим для данной грамматики множества N_A: N_S ={S, T, M}; N_T = {T, M}; N_M = {M}.

После преобразования грамматики она примет вид:

ST+S MT(S) i ;

T MT (S) i ;

M (S) i .

В данном случае преобразование грамматики не привело к её упрощению, но построенные синтаксические деревья будут иметь меньшую глубину, и построение дерева будет происходить быстрее.

Грамматика называется неукорачивающей, если для любого правила грамматики  выполняется. Такое определение применимо как к КС-грамматикам, так и к КЗ-грамматикам. А-грамматика также может быть неукорачивающей. Для КС и А-грамматик необходимым и достаточным условием принадлежности к классу неукорачивающих грамматик является отсутствие в них -правил.

Грамматика называется приведенной, если она неукорачивающая и не содержит непроизводящих символов.

Поэтому, если L(G), то существует приведенная грамматика G₁, такая, что L(G₁)=L(G).

В случае же L(G), существует эквивалентная грамматика с единственным укорачивающим правилом.