Конспект лекций москва 2004 удк 519. 713(075)+519. 76(075) ббк 22. 18я7

Вид материала

Конспект

Содержание 11.1. Типовая задача синтаксического анализа LL(k)-грамматиками называются грамматики, допускающие детерминированное построение левого разбора (left) LL(1)-грамматик. Грамматики могут оказаться LL(k) S  abAabB Теорема 20. LL(k) Использование LL(k) свойства при построении анализатора. LL(1)-грамматика. Тогда существуют два вывода: S

Подобный материал:

• Учебное пособие тверь 2008 удк 519. 876 (075. 8 + 338 (075. 8) Ббк 3817я731-1 + 450., 2962.9kb.
• Тексты лекций Москва 2008 удк 339. 9(075. 8) Ббк 65. 5я73-2, 1528.45kb.
• Программно-технический комплекс Учебное пособие Новочеркасск юргту (нпи) 2010. Удк, 3911.73kb.
• Удк 152. 27 (075. 8) + 157 (075. 8) + 152. 3 (075, 60.12kb.
• Краткий конспект лекций Кемерово 2002 удк: 744 (075), 1231.26kb.
• Методические указания по курсу Новосибирск 2004 ббк ю 937. 4 Удк 152. 26 (075), 802.63kb.
• Москва 2011 ббк 63. 3 (2)я 7 к 90 удк 947 (075) История России, 110.08kb.
• Курс лекций Гродно 2005 удк 631. 1 (075., 1193.16kb.
• Удк 070(075. 8) Ббк 76. 01я73, 5789.66kb.
• Удк 339. 9(470)(075. 8) Ббк, 7329.81kb.

11.1. Типовая задача синтаксического анализа

Имеется активный нетерминал S, множество альтернатив для него S___k и текущее состояние анализируемой цепочки y.

Пусть выбрана альтернатива SX₁X₂…X_n, X_iV_NV_T, при i[1,n].

Если X₁ V_T, то он должен совпадать с первым символом цепочки y. Если совпадает, то укорачиваем цепочку на этот символ и переходим к X₂. Если не совпадает, то переходим к другой альтернативе.

Если же X_iV_N, тогда из X_i необходимо вывести какое-нибудь начало цепочки y. Если из X_i нельзя вывести никакое начало цепочки y, то возможны 2 варианта:

1. Перейти к X_i-1 и попытаться вывести из X_i-1 другое начало и т.д. ( получаем полный перебор вариантов вывода) – разбор с медленным возвратом.

2. Сразу отказаться от альтернативы SX₁X₂…X_n и выбрать другую (разбор с быстрым возвратом).

Очевидно, что наиболее удобными при анализе цепочек являются грамматики, допускающие детерминированный разбор, когда на каждом шаге мы можем однозначно выбрать альтернативу, и в случае невозможности подобрать нужную альтернативу цепочка не принадлежит языку (никакой вывод не может быть построен). Одним из таких типов грамматик являются LL(k)-грамматики.

11.2. LL(k)-грамматики

LL(k)-грамматиками называются грамматики, допускающие детерминированное построение левого разбора (left) при чтении анализируемой цепочки слева (left) направо, при подсматривании вперед не более чем на k символов.

Например, рассмотрим грамматику G₁₈ с множеством правил:

S 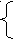a SbB;

B  b B .

Эта грамматика является LL(1)-грамматикой, т.к. для выбора правильной альтернативы на каждом шаге нам достаточно анализировать один (текущий) символ цепочки.

Грамматика называется разделённой, если все правила грамматики имеют вид:Aa₁₁a₂ ₂…a_k_k, причём a_ia_j при ij, a_iV_T, _i(V_TV_N)* при i[1,k]. Очевидно, что в случае разделённой грамматики строится детерминированный нисходящий разбор.

Очевидно, что разделённые грамматики принадлежат к классу LL(1)-грамматик.

Грамматики могут оказаться LL(k)-грамматиками для различных k, например, грамматика может быть LL(3)-грамматикой, но не LL(2)-грамматикой. Бывают и грамматики, которые не являются LL(k)-грамматикой ни для какого k.

Н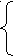апример, рассмотрим грамматику G₁₉ с множеством правил:

S 0 A0B

A  0 A ac L(G)= {0ⁿ⁺¹ c aⁿ, 0ⁿ⁺¹ d bⁿ, n 0}

B  0 B bd

В этой грамматике возможны выводы: S A ⁿ⁺¹0ⁿ⁺¹ с aⁿ и SB ⁿ⁺¹ 0ⁿ⁺¹ d bⁿ ( n  0 ).

Чтобы определить по заданной терминальной цепочке, какое правило ( S  A или S  B ) было применено на первом шаге вывода, нужно прочитать n+1 символ, следовательно данная грамматика не является LL(k) ни при каком k.

Дадим формальное определение LL(k) грамматики. Для этого введем определение



т.е. определяются первые k символов терминальной цепочки. Так как для пустой цепочки это пустое множество, то определим для данной грамматики пополненную грамматику, в которой не будут встречаться пустые цепочки:

Для грамматики G=< V_N, V_T, S, R> соответствующая пополненная грамматика G’=< V_N{S’}, V_T{$}, S’, R’>, где множество правил R’=R{S’ S $ }, здесь каждая цепочка имеет справа граничный маркер ($).

Расширим определение множества так, чтобы охватить произвольные цепочки (V_TV_N)*:

Для (V_TV_N)* First_k()= { x/ * Z, ZV_T*, x=}.

Н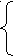апример, рассмотрим грамматику G₂₀ с множеством правил

S  abAabB;

A  ab A c; L(G)= {(ab)ⁿc, (abc)ⁿ, n 1}

B  cab Bc .

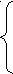Правила соответствующей пополненной грамматики:

S’ S $;

S ® abA½abB;

A ® ab A ½c;

B ® cab B½c.

Для данной грамматики

First₁(S’)=First₁(S)={a}, First₁(A)={a, c}, First₁(B)={c}; First₂(S)={ab}, First₂(A)={ab, c}, First₂(B)={c, ca}, First₂(S’)= =First₂(S)={ab}; First₃(S)= First₃(S’)={abc, aba}, First₃(A)={abc, aba, c}, First₃(A$)={abc, aba, c$},First₃(B)={c, cab}, First₃(B$)={c$, cab}.

Тогда мы можем формально определить LL(k)-грамматику как грамматику, для которой для любых двух левых выводов

S* A      * x

S* A      * y

AV_N, , x, y  V_T*,     (V_N  V_T)*, из условия First_k(x)=First_k(y) следует .

Несложно показать, что данное формальное определение соответствует неформальному.

Теорема 20. LL(k)-грамматика является однозначной.

Неоднозначность грамматики противоречит LL(k) свойству. Неоднозначна – значит, существуют два вывода для некоторой цепочки, поэтому не сможем определить по k символам, какое из правил следует применить.

Теорема 21. КС-грамматика G=< V_N, V_T, S, R> является LL(k)-грамматикой  для любых двух правил А₁ и А₂ и для любой цепочки , такой что S*A из условия ₁₂ следует, что First_k(₁ ) First_k(₂ )=.

Использование LL(k) свойства при построении анализатора.

1. Пусть текущее состояние левого вывода цепочки z=y имеет вид А, где  – выведенное терминальное начало цепочки, А – текущий нетерминал( самый левый нетерминал), y – не просмотренная часть цепочки.
   
2. Рассмотрим First_k(y). Пусть для нетерминала А существуют альтернативы: А₁₂_n R. Надо найти _i для применения на данном шаге.
   
3. Вычисляем = First_k(_i). Это множество может быть заранее вычислено для всех А, , _i. При этом из LL(k) свойства следует, что 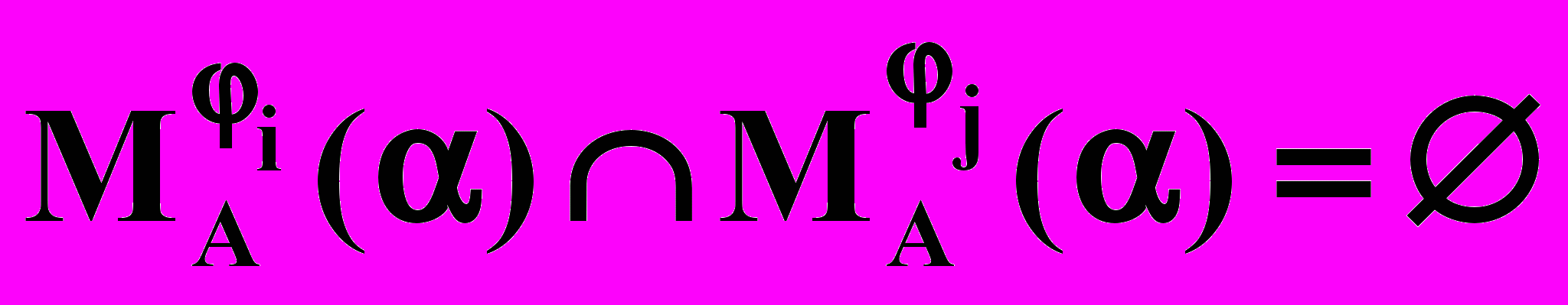при ij.
   
4. Выбираем _i, такое, что First_k(y)= First_k(_i). Если такого _i нет, то zL(G).
   
5. Переходим к анализу полученной цепочки ’y’ (xy’y’), где ’ – терминальное начало цепочки ₁. Шаги повторяются, пока не разберём всю цепочку, или не установим, что zL(G).
   

Пример:

Рассмотрим анализ цепочки acbbd в грамматике G₂₁

S 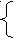ac SbB;

B  b Bd.


Эта грамматика является LL(1) грамматикой. На первом шаге определяем, какое правило применялось вначале: First₁(acS)={a}, First₁(bB)={b}, поэтому на первом шаге применяется правило S ac S, выведенная цепочка принимает вид: acS, First₁(bbd)={b}, поэтому применяется правило S  bB, и выведенная цепочка принимает вид acbB. Определяем First₁(bB)={b}, First₁(d)={d}, поэтому применяемое правило B  b B, выведенная цепочка принимает вид acbbB, применяем правило B  d, получаем исходную цепочку acbbd, значит, анализируемая цепочка принадлежит языку, порождаемому грамматикой.

Проблемы, возникающие при построении анализатора для LL(k)-грамматик:

1. При k1 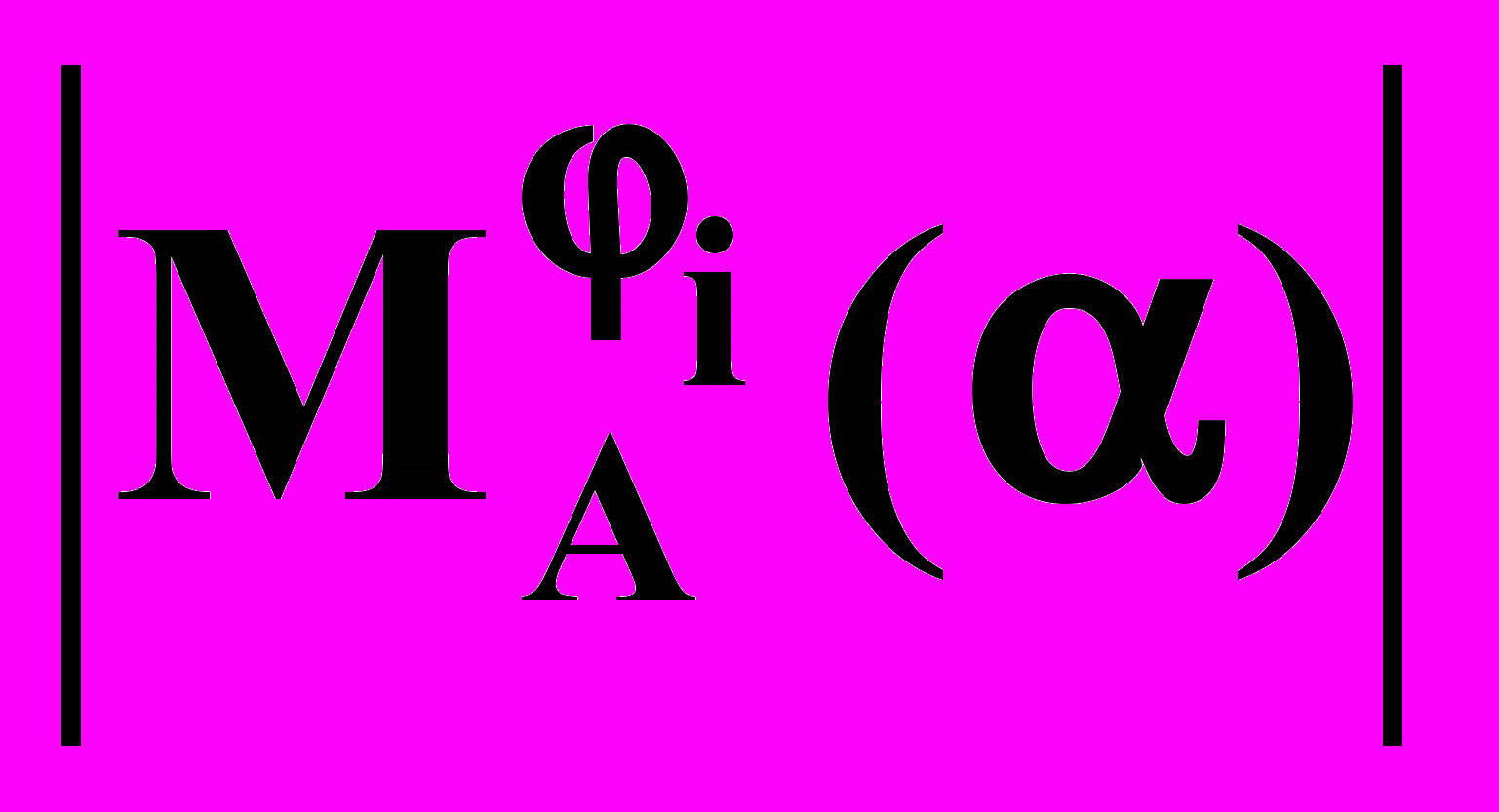может стать неприемлемо большой, т.к. 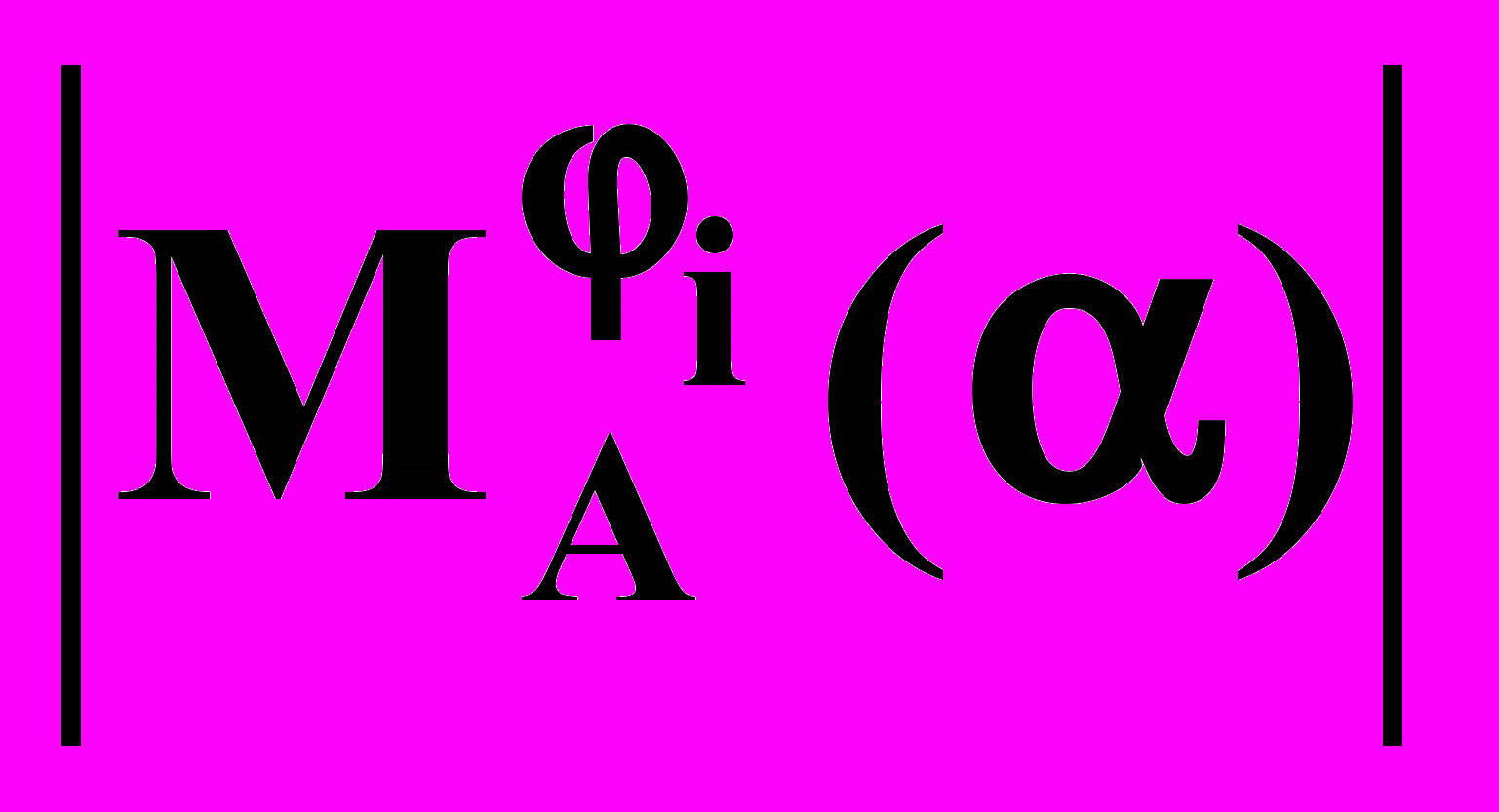пропорциональна k.

2. является функцией от трёх переменных: А, _i, , т.е. велик сам объём предварительных вычислений.

Однако можно упростить задачу, усилив условия, накладываемые на грамматику.

Обозначим и потребуем, чтобы при ij.

Грамматика G называется строго LL(k)-грамматикой, если для любых двух левых выводов

S*₁ A ₁ ₁  ₁ *₁x

S*₂A ₂  ₂  ₂  *₂ y

AV_N, ₁, ₂, x, y  V_T*, ₁ ₂    (V_N  V_T)*, из условия First_k(x)=First_k(y) следует .

Несложно показать, что G является строго LL(k)-грамматикой  для любого AV_N из того, что AR, AR, , следует M_A^M_A^=.

Теорема 22. LL(1)-грамматика всегда строго LL(1)-грамматика.

Доказательство.

Предположим, что некоторая грамматика G – LL(1) грамматика, но не строго LL(1)-грамматика. Тогда существуют два вывода:

S*₁ A ₁ ₁  ₁ * ₁x₁₁* ₁x₁y₁

S*₂A ₂  ₂  ₂  * ₂ x₂₂* ₂ x₂y₂,

(AV_N, ₁, ₂, x₁,y₁, x₂,y₂  V_T*, ₁ ₂    (V_N  V_T)*), такие, что First₁ (x₁y₁) = First₁(x₂y₂) &  – Условие (*).

Но так как G – LL(1)-грамматика, то

S* ₁ A ₁ ₁  ₁* ₁x₁₁ * ₁x₁y₁

S* ₁ A ₁ ₁  ₁* ₁x₂₁* ₁x₂y₁

(AV_N, ₁, ₂, x₁,y₁, x₂ V_T*, ₁ ₂    (V_N  V_T)*) и из First₁ (x₁y₁) = First₁(x₂y₁) следует  – Условие (**).

Покажем, что условия (*) и (**) несовместны.

Рассмотрим следующие случаи:

1. x₁, x₂ , тогда First₁(x₁y₁)=First₁(x₁), First₁(x₂y₂)=First₁(x₂), First₁(x₁ )=First₁(x₂) и, по условию (*), .

С другой стороны, по условию (**), из First₁(x₁ )=First₁(x₂) следует . Противоречие.

2. x₁=, x₂= приводит к неоднозначности грамматики.

3. Пусть x₁=, x₂. Тогда в условии (*)First₁(x₁y₁)=First₁(y₁)= =First₁(x₂y₂)=First₁(x₂) & .

По условию (**) First₁(x₁y₁)=First₁(y₁)= First₁(x₂y₁)=First₁(x₂) & =. Противоречие.

4. Случай 4, x₁¹l, x₂=l разбирается аналогично случаю 3.

Из теоремы следует критерий принадлежности грамматики классу LL(1):

G – LL(1) грамматика  AV_N, , AR & AR & &   M_A^M_A^=, где M_A^b=

При этом если

а) , *, , то M_A^=First₁()

б) *, M_A^=First₁()

Определим множество Follow₁(X)={a/ S⁺Xa&aV_T}, для X(V_NV_T).
Тогда условие б) можно переписать следующим образом:

б) *, M_A^=First₁()Follow₁(A).

Так как рассматриваем пополненную грамматику, то  (First₁()=).

Определения и алгоритмы нахождения множеств First и Follow

1. First₁()

1.1. First₁()=

1.2. aV_T First₁(a)=a

0. First₁(A)={ First₁(x_i) / Ax₁x₂…x_nR & (i=1  i=m &
   

& x₁…x_m-1⁺)}

1.4. First₁(x₁x₂…x_n)={ First₁(x_i)/ i=1i=m&x₁…x_m-1⁺}

Например, рассмотрим грамматику G₂₂ с правилами:

S  ABCCA;

Aa;

B  b B;

CcCd .

В пополненной грамматике добавляется начальное правило S’ S$:

S’ S $;

S  ABCCA;

Aa;

B  b B;

CcCd .

First₁(A)={a};

First₁(B)={b};

First₁(C)={c,d};

First₁(S)= First₁(ABC) First₁(CA)={a, b, c, d}.

1. Follow₁(A)= ={First₁()/ S * A  }. Рассматриваем грамматику без непроизводящих правил, тогда если S * B    A  , то First₁( ) Follow₁(A).
   
   1. , *, , тогда First₁()=First₁().
      
   2. *, тогда First₁()=First₁()First₁().
      

Поэтому Follow₁(A)={ First₁(X_m)/ B A X₁ X₂…X_nR &

& (m=1X₁X₂…X_m-1*)} {Follow₁(B)/B A  R &*}

То есть просматриваются все правые части правил, в которые входит исследуемый нетерминал.

Рассмотрим пополненную грамматику G₂₃, в этой грамматике N_={A,B};

Follow₁(S)={$},

Follow₁(A)= First₁(B) First₁(C)  Follow₁(S)={b, c, d, $},

Follow₁(B)= First₁(C)={c,d},

Follow₁(C)= First₁(A)  Follow₁(S)={a,$}.

Проанализируем LL(1)-свойство грамматики:

M_S^ABC= First₁(A) First₁(B) First₁(C)={a, b, c, d},

M_S^CA= First₁(C)={c,d}.

Так как M_S^ABC M_S^CA , то грамматика не является LL(1) –грамматикой.