Конспект лекций москва 2004 удк 519. 713(075)+519. 76(075) ббк 22. 18я7

Вид материала

Конспект

Содержание 12.2. Автоматы Мура

Подобный материал:

• Учебное пособие тверь 2008 удк 519. 876 (075. 8 + 338 (075. 8) Ббк 3817я731-1 + 450., 2962.9kb.
• Тексты лекций Москва 2008 удк 339. 9(075. 8) Ббк 65. 5я73-2, 1528.45kb.
• Программно-технический комплекс Учебное пособие Новочеркасск юргту (нпи) 2010. Удк, 3911.73kb.
• Удк 152. 27 (075. 8) + 157 (075. 8) + 152. 3 (075, 60.12kb.
• Краткий конспект лекций Кемерово 2002 удк: 744 (075), 1231.26kb.
• Методические указания по курсу Новосибирск 2004 ббк ю 937. 4 Удк 152. 26 (075), 802.63kb.
• Москва 2011 ббк 63. 3 (2)я 7 к 90 удк 947 (075) История России, 110.08kb.
• Курс лекций Гродно 2005 удк 631. 1 (075., 1193.16kb.
• Удк 070(075. 8) Ббк 76. 01я73, 5789.66kb.
• Удк 339. 9(470)(075. 8) Ббк, 7329.81kb.

12.2. Автоматы Мура

Автоматы Мура отличаются от автоматов Мили тем, что здесь одному состоянию (а не переходу) соответствует один выход.

Конечный автомат Мура: S=< V_a, Q, V_b, q₀, F, G>, где

V_a={a₁,a₂,…, a_m}, m1 – входной алфавит автомата,

V_b= {b₁, b₂, …, b_n}, n1 – выходной алфавит автомата,

Q = {q₀,q₁,…, q_k}, k0 – внутренний алфавит (алфавит состояний),

q₀Q – начальное состояние автомата (инициальный автомат, иногда рассматривают q₀= q(0)),

F – функция переходов; F: Q V_a Q,

G – функция выходов, G: Q  V_b .

Приняты две схемы задания автоматов Мура:

Первая схема	Вторая схема
q 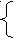(t+1) =f (q(t), a(t)) b(t)= g(q(t))	q 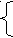(t+1) =f (q(t), a(t)) b(t)= g(q(t+1))

При работе по первой схеме выход автомата однозначно соответствует состоянию, из которого совершается переход, по второй – состоянию, в которое автомат переходит. Хотя при записи уравнений первая схема выглядит более естественно, условие второй схемы реализовать проще: в соответствующих автоматах Мили для первой схемы должны быть одинаковые выходы на всех дугах, выходящих из состояния, для второй – одинаковые выходы должны быть на дугах, ведущих в состояние. Первое условие может выполняться, а может и не выполняться, выполнения второго условия можно достичь с помощью эквивалентного преобразования автомата.

Рассмотрим автомат Мура, представленный на рис. 27



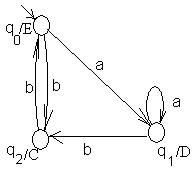
Рис.27

Здесь выходы, соответствующие состояниям, изображены справа от состояния. Если рассматривать работу автомата по первой схеме, то входу aabb будет соответствовать выход EDDC, если же по второй схеме, то этому же входу соответствует выход DDCE.

По автомату Мура всегда можно построить автомат Мили.

Автомат Мили, эквивалентный автомату Мура, представленному на рис. 27, при работе по первой схеме, дан на рис. 28(все дуги, ведущие из состояния, имеют одинаковые выходы), а при работе по второй схеме – на рис.29 (все дуги, ведущие в состояние, имеют одинаковые выходы).

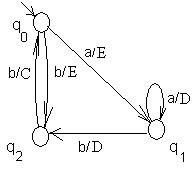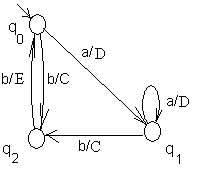Рис.28	Рис.29

Очевидно, что по автомату Мура всегда можно построить автомат Мили.

По выразительной мощности эти модели (автоматы Мили и Мура) эквивалентны, если используется вторая схема для представления автоматов Мура.

Построение автомата Мура (вторая схема) по автомату Мили:

а) если все дуги, ведущие в некоторое состояние q_k, имеют одинаковые выходные пометки b_s, то эта пометка просто переносится на это состояние (рис.30).



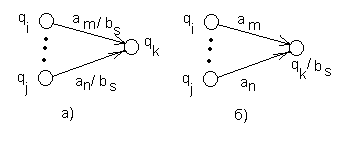
Рис. 30

Формально это условие для состояния q_k и выхода b_s можно записать так:

q_i,q_j,a_n,a_m (f(q_i,a_n)= f(q_j,a_m)= q_k  g(q_i,a_n)= g(q_j,a_m)= b_s);

б) общий случай: в некоторые вершины ведут дуги, помеченные разными символами. В этом случае все такие вершины q_k расщепляются на множество вершин (расщепление состояния), помечаемых символами _k,b_j> (рис.31). Условная запись расщепления состояний:q_k{_k, b_j>/ f(q_i, a)=q_k, g(q_i, a)=b_j}



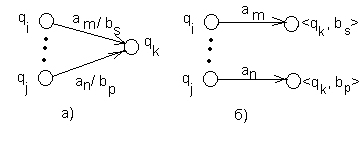
Рис. 31

В общем случае число состояний увеличивается. Затем для каждого состояния q_i исходного автомата Мили и для каждой дуги из состояния q_i в состояние q_k с пометкой a_p/b_s (a_p – вход, b_s – выход) строятся дуги из всех _i,b_j> в _k, b_s> и помечаются a_p.

Кроме того, если начальное состояние q₀ расщепилось, вводится новое начальное состояние, в которое не ведет ни одна дуга.

Затем приписываем состояниям соответствующие выходы и переобозначаем состояния.

Например, рассмотрим автомат Мили (рис. 32, а), приведенный так же на рис. 25. У этого автомата состояния q₁ и q₂ расщепляются, а q₀ не расщепляется, поэтому новое входное состояние не вводится. Полученный эквивалентный автомат Мура приведён на рис. 32,б. Тот же автомат после переобозначения состояний приведен на рис. 32,в.





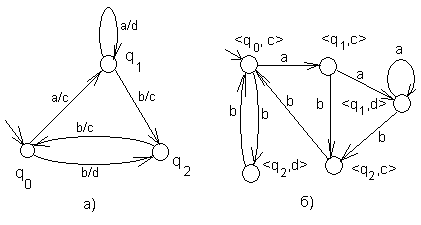
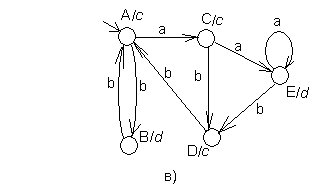
Рис. 32

Полный алгоритм построения эквивалентного автомата Мура по автомату Мили выглядит следующим образом:

1. расщепляем состояния;
   
2. вводим дополнительное входное состояние (если входное состояние расщепилось);
   
3. строим дуги, соответствующие дугам исходного автомата;
   
4. переносим выходные символы на соответствующие состояния;
   
5. переобозначаем состояния.
   

Таким образом, установлено соответствие между разными типами автоматов.