Учебное пособие йошкар-Ола, 2001 ббк у053 П815

Вид материала

Учебное пособие

Содержание Симплексный метод Х1 – количество изделий 1, которые могут быть изготовлены сверх плана, через Х Применение СПУ в экономическом анализе РН принимается из времени РО РО работ, чтобы не увеличить выполнение всего комплекса работ. Определяется оно как разность между ПО Методы, используемые в анализе Xij на всех этапах транспортной задачи должно быть равным m + n –1

Подобный материал:

• Учебное пособие Йошкар-Ола 2008 удк 378. 2 Ббк 74., 2437.63kb.
• Учебное пособие г. Йошкар Ола, 2007 Учебное пособие состоит из двух частей: «Книга, 56.21kb.
• Учебное пособие Йошкар-Ола, 2008 ббк п6 удк 631. 145+636: 612. 014., 7797.37kb.
• Постановление мэра города Йошкар-Олы, 281.53kb.
• Дисциплина «Статистика» Список литературы, 13.17kb.
• Семинар №5 Йошкар Ола, 25 февраля 2010 года «Новейшие изменения корпоративного законодательства», 33.44kb.
• Учебно-методическое пособие Йошкар-Ола, 2009 ббк п 6 удк 636, 3772.57kb.
• Ю. А. Александров Основы радиационной экологии Учебное пособие, 5090.11kb.
• Исполнителем мероприятий Программы является Министерство внутренних дел Место нахождения, 77.66kb.
• Постановление мэра города Йошкар-Олы, 220.5kb.

Проверка Плана 2 на оптимальность:

m + n – 1 = 3 + 4 – 1 = 6 – это условие отвечает критерию
оптимальности;

исследуются неиспользованные пункты (А₁В₂, А₁В₃, А₂В₁, А₂В₄, А₃В₁ и А₃В₂) аналогично тому, что выполнено в п.2. Процесс продолжается до тех пор, пока будут иметь место пункты, дающие экономию транспортных затрат.

Примечание:

После получения очередного плана необходимо определить величину транспортных затрат и экономию их по сравнению с первым
в абсолютном и относительном выражении. Так по второму плану они составляют

ТЗ₂ = 15 (22) + 5 (17) + 19 (15) + 11 (20) + 17 (11) + 28 (25) =

= 1807 ден.ед.

Экономия по сравнению с первым планом составляет:

в абсолютном выражении Э_абс = 1807 – 1947 = 140 ден.ед.;

в относительном выражении



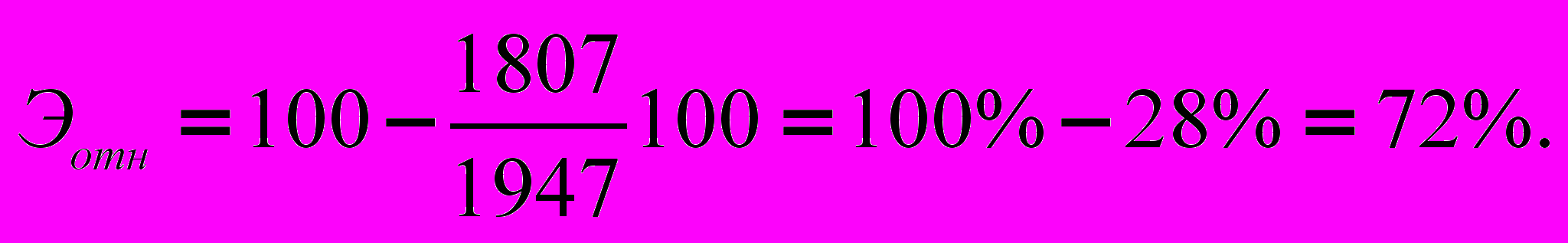
При решении транспортных задач используются и другие алгоритмы, позволяющие сократить вычислительный процесс, затраты времени и в результате этого получить экономию.

Дальнейшее решение предлагается выполнить студентам по указанному выше алгоритму.

Симплексный метод

Среди различных методов решения планово-экономических задач большое применение получил симплексный метод.

Основная задача линейного программирования, решаемая симплексным методом состоит в следующем.

Найти такие неотрицательные значения неизвестных Х₁, Х₂, … Х_n,
которые придавали бы максимум или минимум линейной функции



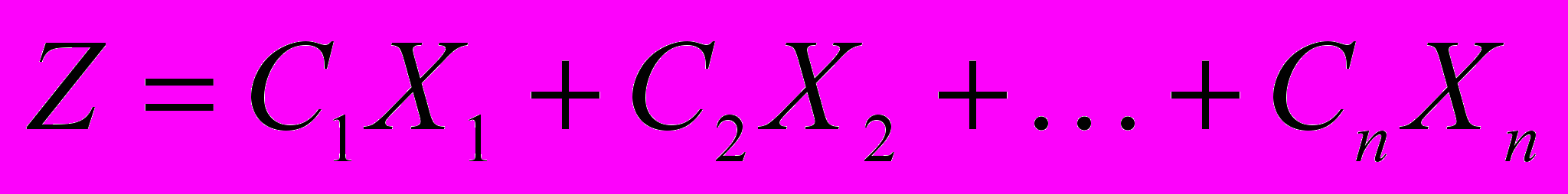
и удовлетворяли бы следующей системе уравнений



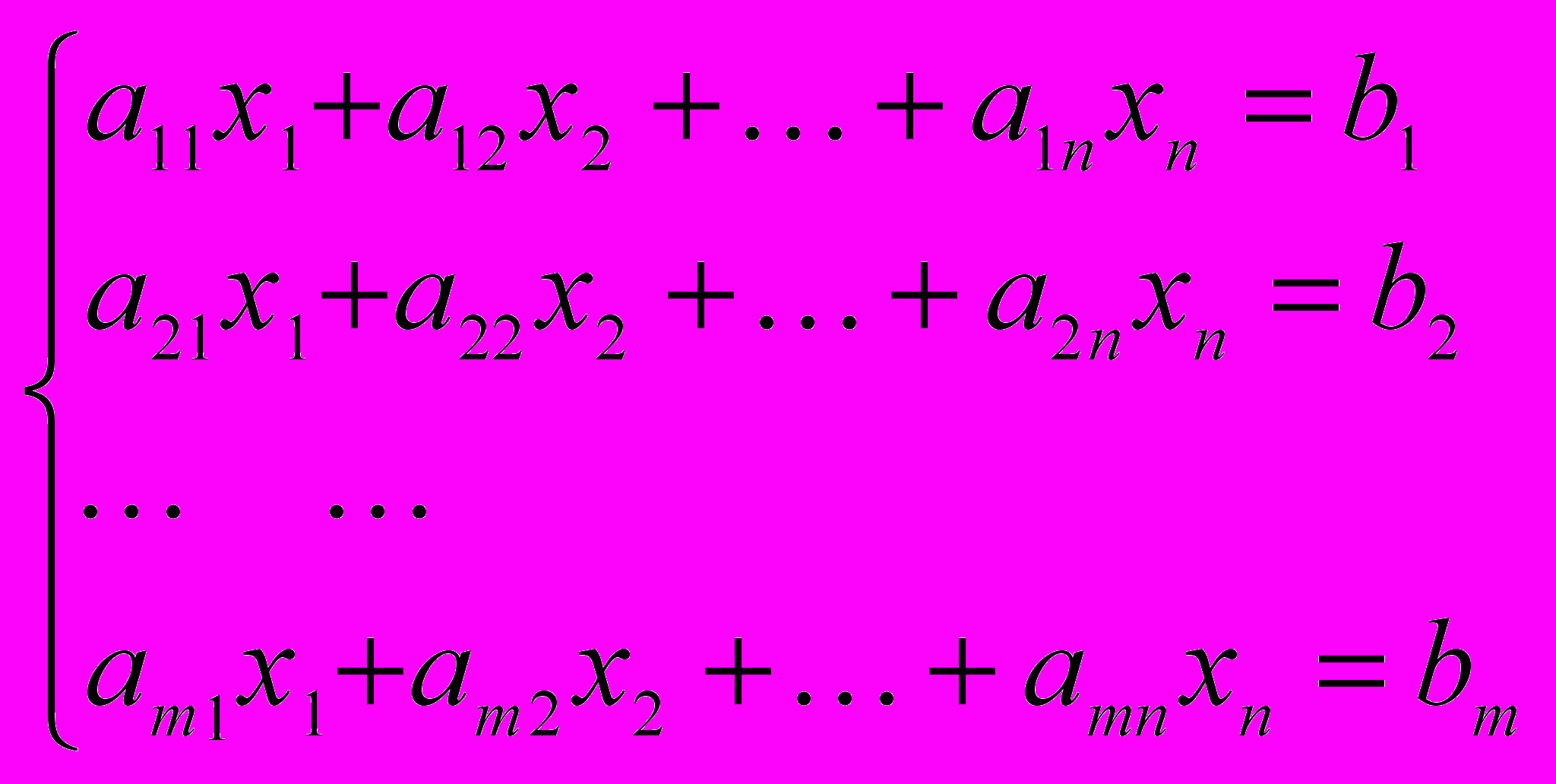
где:

c₁ , c₂ , … c_n – известные числа;

a₁₁, a₁₂ …. a_1n – наперед заданные числа;

b₁ , b₂ , … b_m – наперед заданные числа;

x_i > 0, где i = 1,2, … n.

Пример 39

Пусть цех выпускает четыре вида различных изделий. Для цеха установлен следующий сменный план выпуска изделий: 1 изделия – 100 ед., 2 изделия – 80 ед., 3 изделия – 60 ед., 4 изделия – 50 ед.

Для выполнения плана цех располагает следующими сменными ресурсами: А – производственного оборудования – 880 ед., Б – сырья – 800 ед., В – электроэнергии – 950 ед.

Расход ресурсов на одно изделие представлен в следующей таблице:

Ресурсы	Изделия
1	2	3	4
Оборудование	2	3	2	4
Сырье	1	2	3	4
Электроэнергия	2	3	4	2

Задана стоимость единицы каждого изделия: 1-го изделия – 5 руб.,
2-го изделия – 6 руб., 3-го изделия – 7 руб., 4-го изделия – 9 руб.

Требуется определить сверхплановый выпуск изделий с максимальной стоимостью.

Решение:

Для выполнения плана требуются следующие затраты:

оборудования – 2(100) + 3(80) + 2(60) + 4(50) = 760 ед.;

сырья – 1(100) + 2(80) + 3(60) + 4(50) = 640 ед.;

электроэнергии – 2(100) + 3(80) + 4(60) +2(50) = 780 ед.

Для перевыполнения плана остается:

оборудования – 120 ед. (880 – 760);

сырья – 160 ед. (800 – 640);

электроэнергии – 170 ед. (950 – 780).

Обозначим через Х₁ – количество изделий 1, которые могут быть изготовлены сверх плана, через Х₂ – то же по изделию 2, Х₃ – по изделию 3 и Х₄ – по изделию 4.

Тогда количество изготавливаемых сверх плана четырех видов изделий должно удовлетворить следующим ограничениям по ресурсам:


.
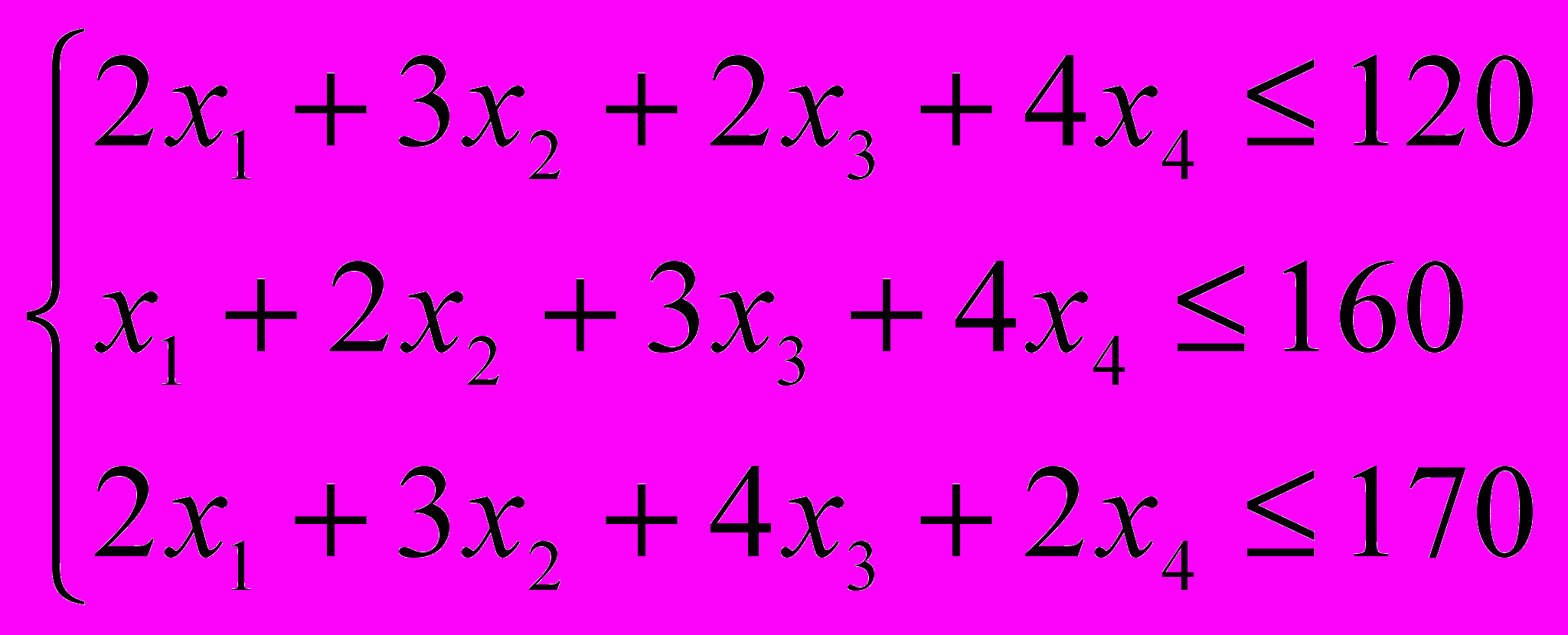
(1)

Эти неравенства показывают, что для получения сверхплановой продукции оставшиеся ресурсы могут использоваться полностью (=) или частично (<).

Найти

Z_max = 5х₁+6х₂+7х₃+9х₄. (2)

Для решения задачи симплексным методом необходимо преобразовать неравенства в эквивалентные равенства путем добавления свободных переменных х₅, х₆, х₇, которые также являются неизвестными. Свободные переменные показывают разность между возможными
и используемыми ресурсами. В результате получается следующая система равенств:


.
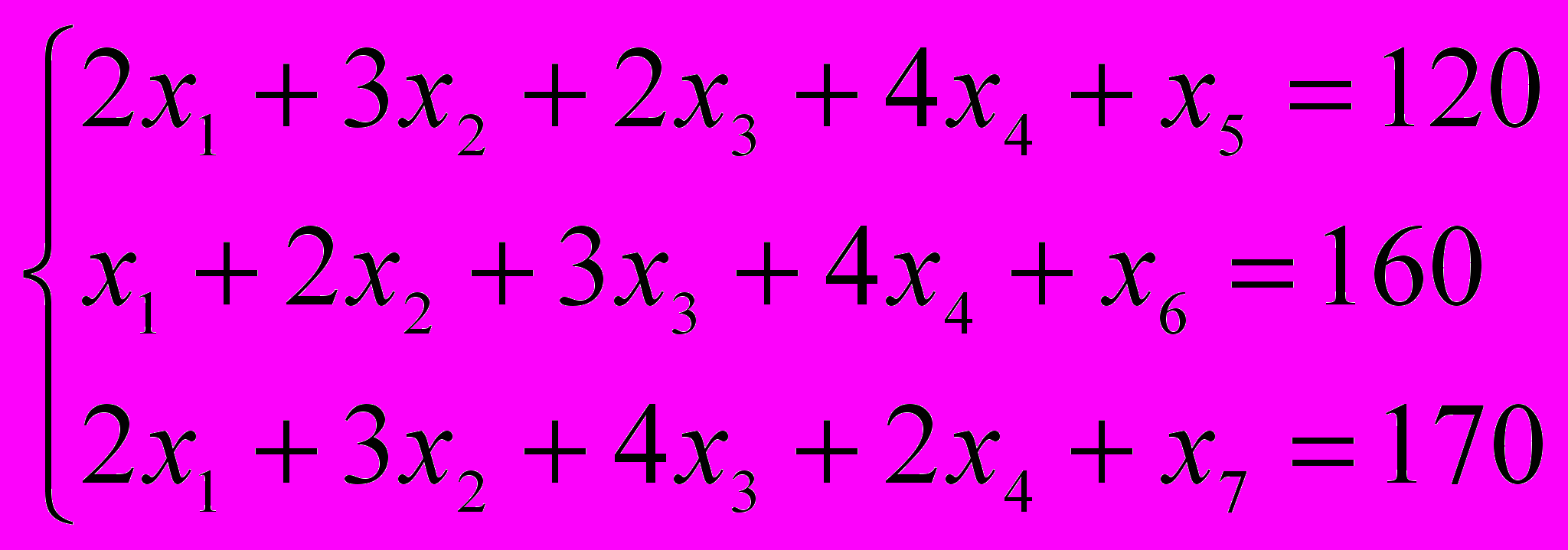
(3)

Эти свободные переменные вводятся в целевую функцию, экстремум которой необходимо определить, то есть

Z_max = 5х₁+6х₂+7х₃+9х₄+0(х₅)+0(х₆)+0(х₇).

Свободные переменные Х_5, Х₆ и Х_7, входят в целевую функцию
с нулевой стоимостью и, следовательно, на ее величину не влияют. Однако эти переменные играют важную роль в методике симплексного метода.

В результате этого получается следующая первая симплексная таблица (первый базовый, опорный план):

План 1

Ci			5	6	7	9	0	0	0	Контрольный столбец
Х0	Х1	Х2	Х3	Х4	Х5	Х6	Х7
0	Х5	120	2	3	2	4	1	0	0	132
0	Х6	160	1	2	3	4	0	1	0	171
0	Х7	170	2	3	4	2	0	0	1	182
Zi –Ci		0	– 5	– 6	– 7	– 9	0	0	0	– 27

Решение:

1. План будет считаться неоптимальным до тех пор пока в строке целевой функции будут сохраняться отрицательные значения (при решении на max и положительные при решении на min).

2. Оптимизация плана начинается с определения продукта (ключевого столбца), включение которого в план приведет к его улучшению. Этот продукт принимается по наименьшей абсолютной величине (это Х₄).

3. Определяется продукт в плане, который следует вывести из плана, ибо он сдерживает улучшений плана. Этот продукт (ключевая строка) определяется путем деления значений векторного столбца, (Х₀) на соответствующие значения ключевого столбца (Х₄): 120:4=30, 160:4=40 и 170:2=85 по наименьшему частному принимается ключевая строка (это Х₅).

4. Значения элементов новой таблицы определяется по следующим правилам:

1) бывший ключевой столбец в новой таблице имеет нулевые значения, кроме разрешающего элемента (r_ij), элемента лежащего на пересечении ключевого столбца – Х₄ и ключевой строки – Х₅, который
в новой таблице принимается за единицу;

2) ключевая строка (Х₅) в новой симплексной таблице принимается путем деления величин элементов старой таблицы на ключевое число, а именно:

120:4=30; 3:4=3/4; 4:4=1; 0; 132:4=33;

2:4=0,5; 2:4=0,5; 1:4=1/4; 0;

3) если в ключевом столбце имеются нули, то соответствующая строка переносится в новую таблицу без изменения (в данной таблице таких строк нет);

4) если в ключевой строке есть нули, то соответствующий столбец переносится в новую таблицу без изменения (в данной таблице это столбцы Х₆ и Х₇);

5) остальные элементы новой симплексной таблицы определяются по формуле

,

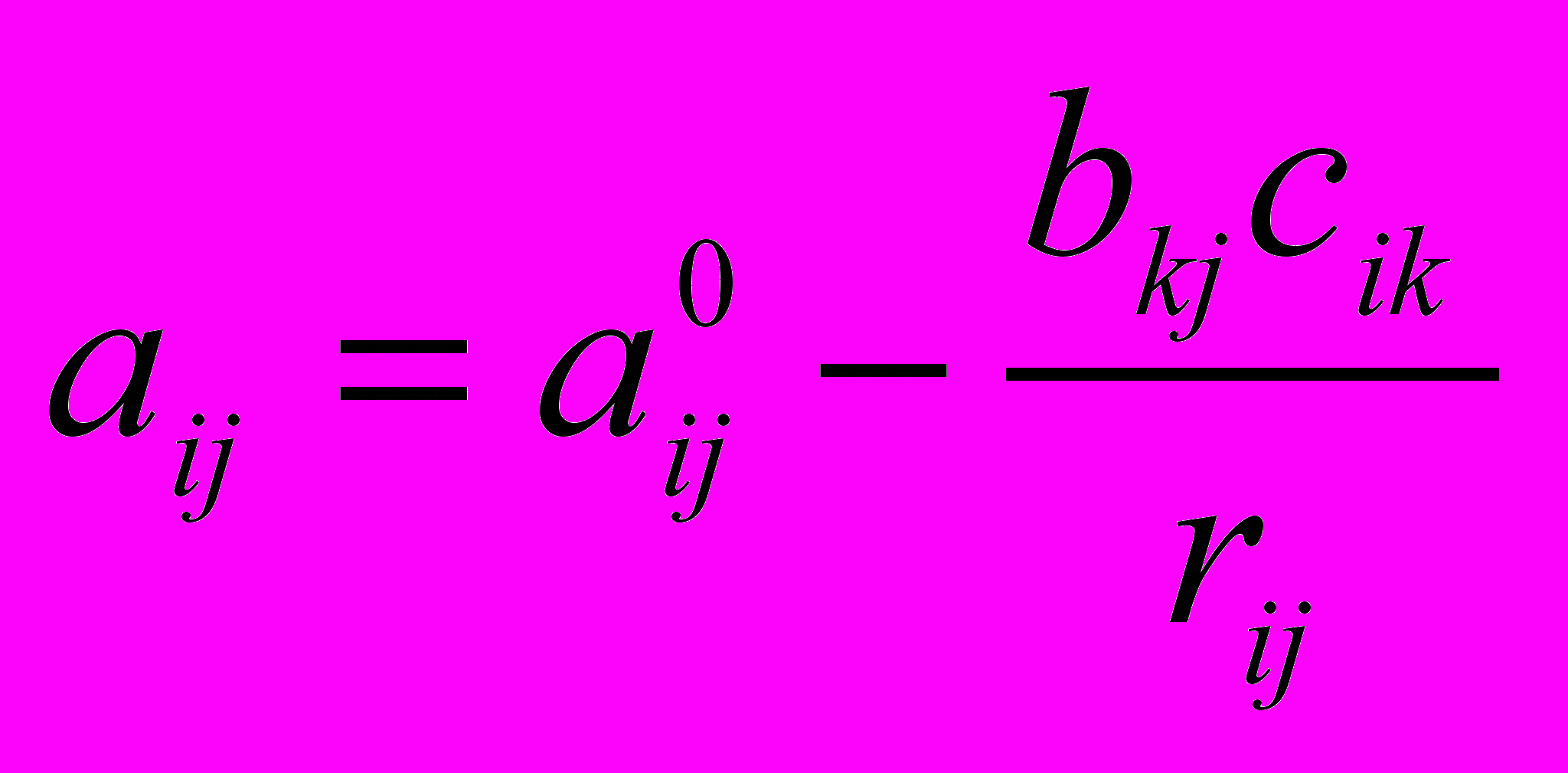где:

a⁰_ij – величина элемента в предыдущей таблице, например для Х_6.0 это 160;

b_kj – значение соответствующего элемента, лежащее в ключевой строке, например для Х_6.0 это 120;

c_ik – значение соответствующего элемента, лежащего в ключевом столбце, например для Х_6.0 это 4.

Откуда:

,

,

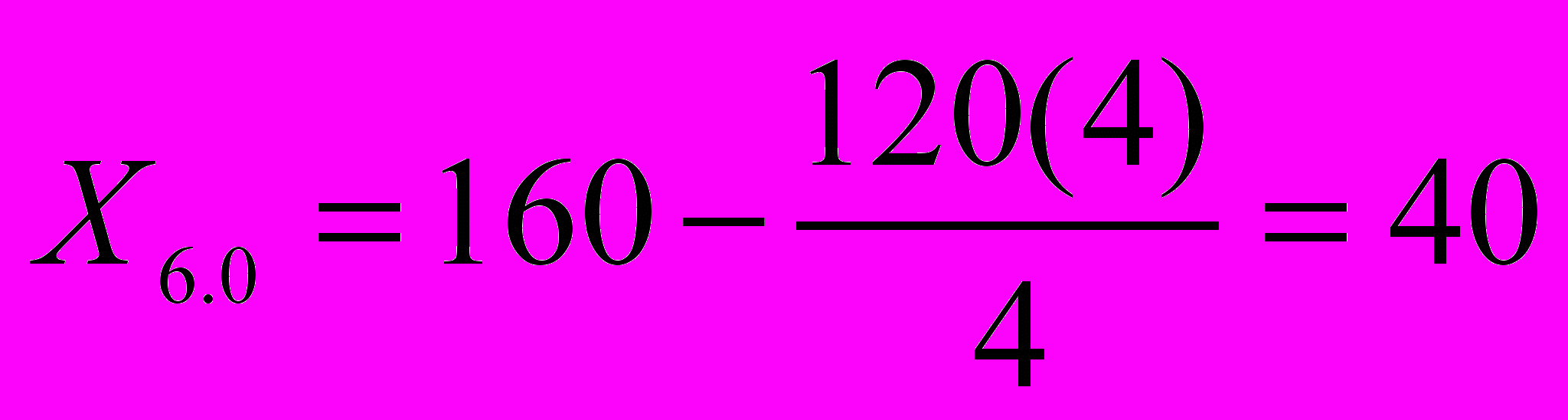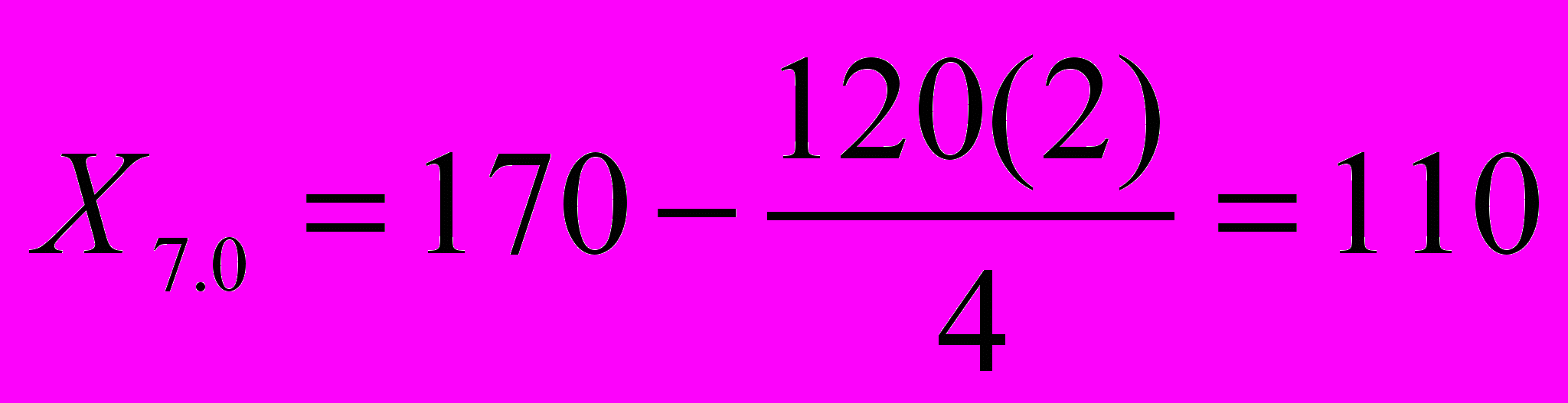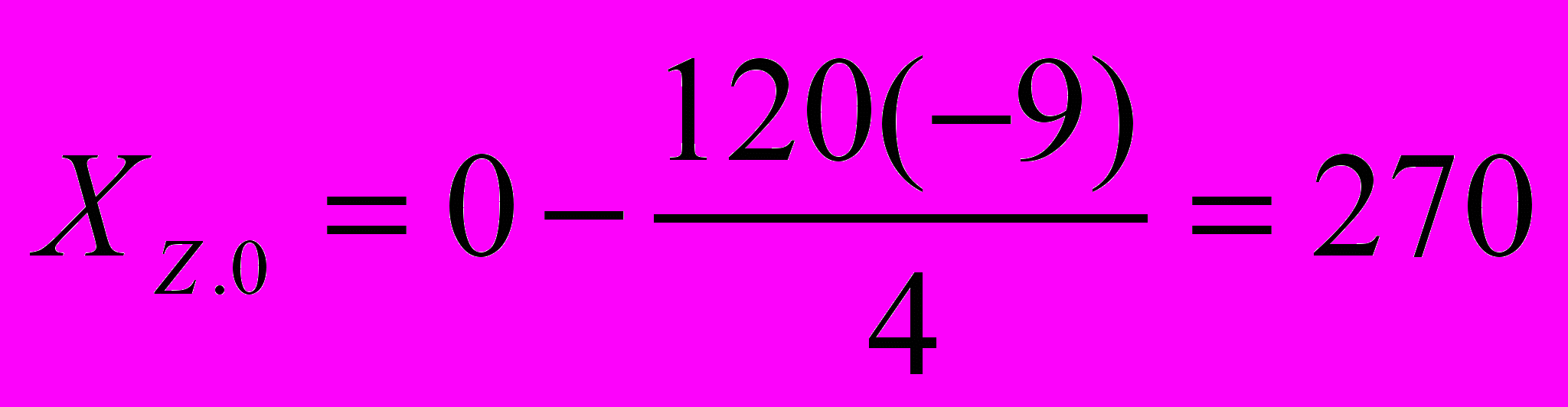и т.д.

Проверка:

Z = 5(Х₁) + 6(Х₂) + 7(Х₃) + 9(Х₄) + Х₆(0) + Х₇(0)

= 5(0) + 6(0) + 7(30) + 9(0) + 0+ +0 + 0 = 270 ден.ед.,

что соответствует расчету элемента

Х_Z.0 = 270 ден. ед.

5. Если в итоговой (целевой) строке имеются отрицательные значения, повторяется эта же процедура: определяется ключевой столбец, ключевая строка, остальные элементы новой симплексной таблицы по правилам упрощенного расчета и по формуле определения оставшихся элементов.

(Дальнейший расчет, предлагается студентам выполнить самостоятельно. По результатам сделать выводы).

Применение СПУ в экономическом анализе

Внедрение достижений научно-технического прогресса в практику на пороге XXI века выявило большой разрыв между его возможностями и методами управления, особенно при разработке больших и сложных систем и комплексов (грандиозных сооружений, тоннелей и мостов через проливы морей и водные бассейны, космических ракет и подводных городов, заводов-городов со сложной и закрытой технологией и других нестандартных объектов).

Ошибки проектирования и претворения проекта в реальность (создания или строительства) вызвали громадные потери во времени, в материалах и денежных средствах. Это послужило основанием поиска таких систем управления, которые содействовали бы устранению разрыва между возможностями НТП и существующей системы управления.

Научные и практические поиски в этом направлении привели
к созданию системы КОППР (критический отбор проектно-плановых решений), вошедшей в последствии как система сетевого планирования и управления (СПУ). Последнее название закрепилось за этим методом в силу того, что его основой является сетевой график. Этот метод позволял устранить недостатки традиционных методов управления, основанных на ленточных диаграммах (графиках Ганта). Последние не позволяли:

1. охватить в единое целое все многообразие работ по созданию сложных систем;
   
2. отразить взаимную связь работ единого, сложного комплекса;
   
3. выявить из всех работ те, от выполнения которых зависит выполнение всего комплекса работ в заданное (планируемое) время, объем, стоимость работ, либо какой другой принятый критерий.
   

Применение метода СПУ позволяет руководству:

1. иметь исчерпывающую информацию о ходе выполнения работ на любой момент времени;
   
2. видеть работы, от выполнения которых в данный момент времени зависит выполнение всего комплекса работ;
   
3. определять критический (напряженный) путь и оперативно содействовать ответственным исполнителям этих работ в соблюдении графиков их выполнения;
   
4. своевременно использовать имеющиеся резервы на ненапряженных работах для выполнения работ, составляющих критический путь.
   

Важнейшим документом при СПУ является сетевой график, представляющий собой графическую модель взаимосвязи между работами. Основными элементами графика являются работы (обычно изображаются стрелками), события (изображаются кружками) и пути (последовательность работ от начального до конечного события).

Работы бывают:

1. реальными (сплошная стрелка), имеют размерность в натуральных, в стоимостных или временных единицах (часы, смены, дни, недели, месяцы);
   
2. фиктивными (пунктирная стрелка), не имеют размерности
   и означают ожидание.
   

События не имеют размерности и означают:

1. работа закончена (для той или тех, которые входят в события);
   
2. работа начата (для той или тех работ, которые выходят из события).
   

Из начального события работы только выходят, в конечное только входят.

Путь в сетевом графике бывает:

1. критический (напряженный), не имеющий резервов времени. Увеличение продолжительности работ на этом пути увеличивает выполнение всего комплекса работ, а сокращение – уменьшает;
   
2. подкритический – путь, занимающий наибольшую напряженность после критического;
   
3. рядовой (обычный, ненапряженный) путь, имеющий резервы времени.
   

Сетевой график имеет следующие параметры:

1. продолжительность выполнения работы – t_ij;
   
2. раннее начало и окончание работы – t_РН;
   
3. позднее начало и окончание работы – t_ПН;
   
4. резервы времени (полный – R_ij и частный – r_ij).
   

Анализ сетевого графика предполагает выявление резервов времени и определение работ, лежащих на критическом пути. Анализ может осуществляться аналитическим, графическим и табличным методами, либо их сочетанием, например, таблично-аналитическим. При использовании последнего исходные данные с графика на рисунке переносят
в таблицу в логической последовательности выполнения работ (см. табл.28).




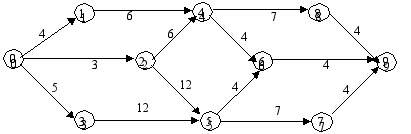
Сетевой график выполнения комплекса работ


Пример 40

По данным сетевого графика на рисунке представленном выше, требуется определить резервы времени и выявить критический путь.

Для определения резервов времени предварительно рассчитывается раннее и позднее время начала и окончания работ. Раннее время начала и окончания работ (РН, РО) определяется прямым ходом, то есть от начального события к конечному. Время РН работ, выходящих из начального события принимается равным нулю, а время РО принимается равным времени РН плюс продолжительность выполнения. При этом время РН последующих работ, выходящих из одного события принимается по наибольшему значению времени РО предыдущей работы, входящее в это событие (например, для работ 4-6
и 4-8 РН принимается из времени РО работ 1-4 и 2-4 не 9, а 10 дней).

Таблица 28

Расчет параметров сетевого графика

Работа, i-j	Продол-житель-ность, дн. ti-j	Время раннего	Время позднего	Полный резерв времени, Ri-j	Частный резерв времени, Ri-j
начала tPH	окончания tPO	начала tПН	окончания tПО
0-1	4	0	4	7	11	7	0
0-2	3	0	3	2	5	2	0
0-3	5	0	5	0	5	0	0
1-4	6	4	10	11	17	7	0
2-4	6	3	9	11	17	8	1
2-5	12	3	15	5	17	2	2
3-5	12	5	17	5	17	0	0
4-6	4	10	14	20	24	10	7
4-8	7	10	17	17	24	7	0
5-6	4	17	21	20	24	3	0
5-7	7	17	24	17	24	0	0
6-9	4	21	25	24	28	3	3
7-9	4	24	28	24	28	0	0
8-9	4	17	21	21	28	7	7

Позднее начало и окончание (ПН и ПО) работ определяется обратным ходом, то есть от конечного события к начальному. В начале определяется время ПО работ, входящих в конечное событие. Оно принимается равным наибольшему значению времени РО. Время ПН работ, входящих в конечное событие равняется разности между временем ПО и продолжительности работ. Время ПО предыдущих работ принимается равным наименьшему значению времени ПН последующих работ, выходящих из данного события. Например, для работ 2-5 и 3-5 время ПО принимается не 20 дней работы 5-6, а 17 дней работы 5-7.

Резерв времени полный – это время, на которое можно перенести время РО работ, чтобы не увеличить выполнение всего комплекса работ. Определяется оно как разность между ПО и временем РО или временем ПН и РН работ.

Частный резерв времени определяется как разность между временем РО и РН и продолжительностью работы. В тех случаях, когда для ряда работ имеется несколько значений времени РО в расчет принимается наибольшее (например, для работы 2-4 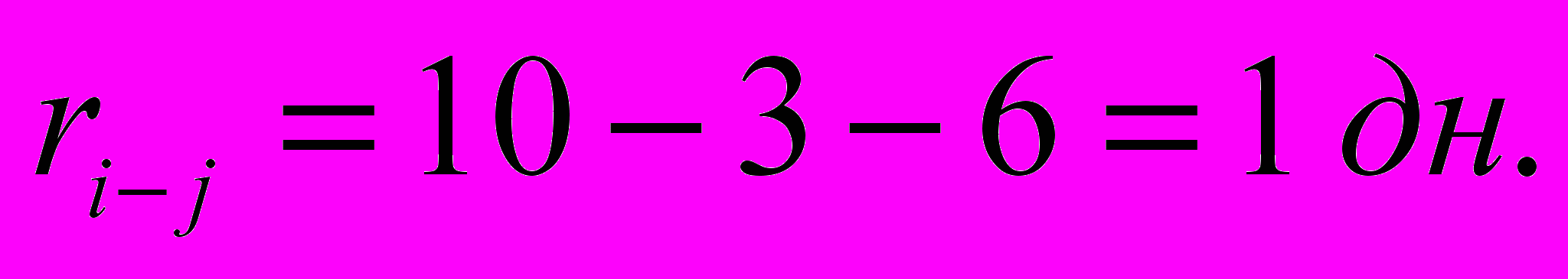, а не 9-3-6, так как событие 4 произойдет лишь через 10 дней, а не 9). Частный резерв времени – это время на которое можно перенести время РН работ, чтобы не увеличить время выполнения всего комплекса работ.

Работы, не имеющие ни полного, ни частного резерва времени является напряженными и их последовательность составляет критический путь. В данном примере это 0-3, 3-5, 5-7 и 7-9.


ТЕМА 6

ЭКОНОМИКО-МАТЕМАТИЧЕСКИЕ
МЕТОДЫ, ИСПОЛЬЗУЕМЫЕ В АНАЛИЗЕ

Транспортные задачи

Важнейшим инструментом экономического анализа является математическое моделирование экономических явлений и процессов.
В экономическом анализе в основном используются математические модели, которые описывают изучаемые явления и процессы в виде неравенств, уравнений и других математических функций.

Наибольшее распространение из экономико-математических методов (ЭММ) в практике экономического анализа получили методы линейного программирования, в частности при решении транспортных
и производственных задач. Так математическая формулировка траспортной задачи состоит в следующем:

имеется m – поставщиков и n – потребителей.

Количество продукции у поставщика i-го составляет – Ai, спрос потребителя j – Bj.

Затраты по перевозке одной машины груза от i-го поставщика к j – му потребителю составляет – Cij : ( Cij  0).

Размер поставки от i к j составляет Xij.

Исходные данные должны удовлетворять следующему условию: наличие продукции у поставщика равно потребностям потребителей
(в случаях их неравенства вводится фиктивный поставщик или потребитель).

.

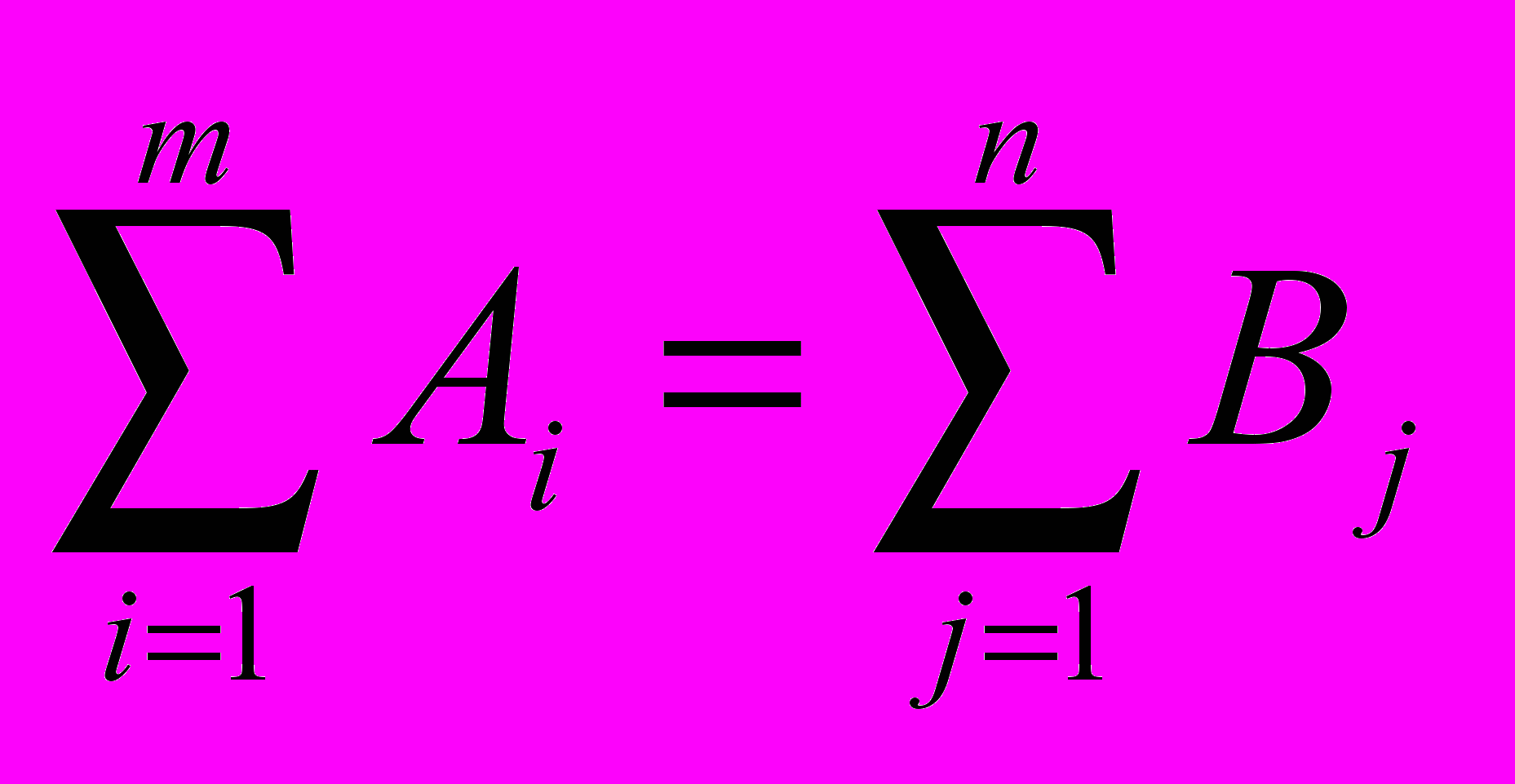Исходное решение отвечает следующей целевой функции:

,

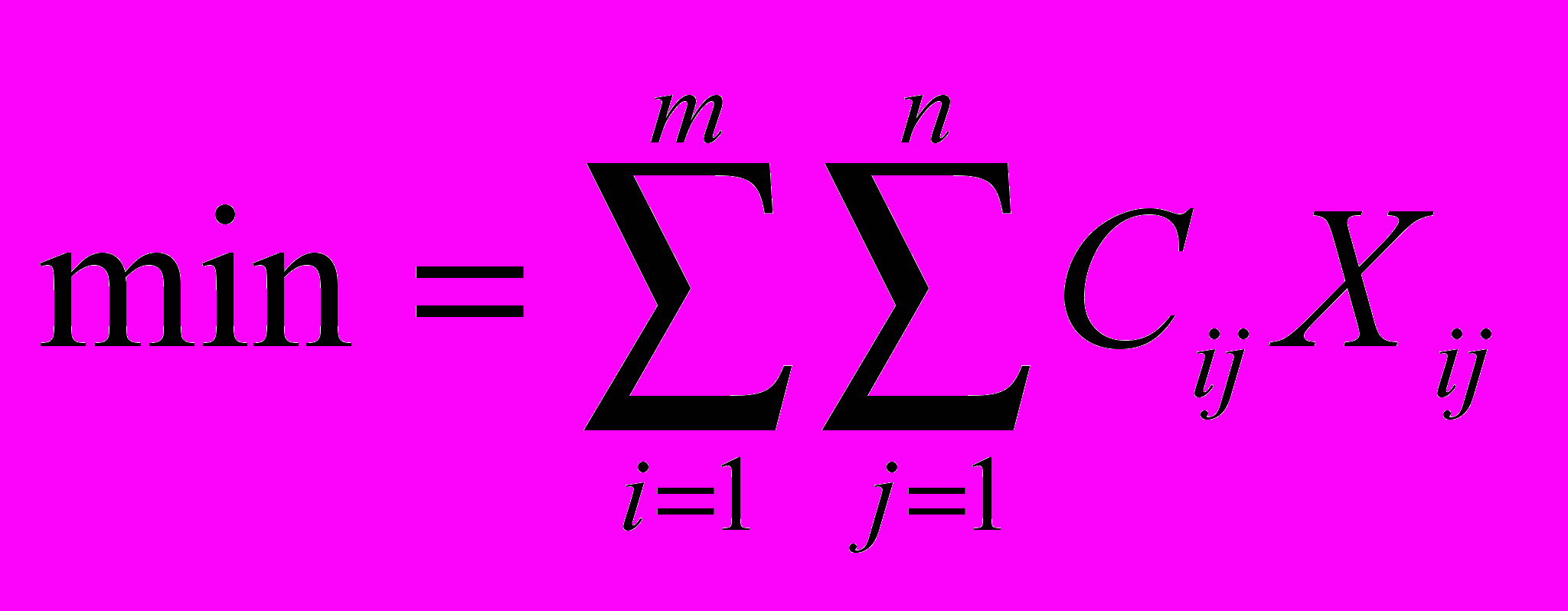то есть затраты по перевозкам должны быть минимальными.

Необходимо отметить, что количество неизвестных Xij на всех этапах транспортной задачи должно быть равным m + n –1, то есть число неиспользованных маршрутов отвечает данной величине. Это и будет первым критерием оптимальности.

Пример 38

Имеется три склада, расположенные в трех пунктах: А₁, А₂, А₃.
В пункте А₁ имеется 20 машин груза, в пункте А₂ – 30, в пункте А₃ – 45 машин груза.

Этот груз должен быть доставлен в четыре пункта назначения В₁, В₂, В₃ и В₄. Причем пункту В₁ необходимо доставить 15 машин груза, В₂ – 19, В₃ – 28 и пункту В₄ – 33 машины груза.

Затраты в денежных (ден.) единицах (ед.) на перевозку одной машины из пункта А_i в пункт B_j представлены в следующей таблице:

Таблица 27

Контрагенты	Потребители
В1	В2	В3	В4
Постав-щики	А1	22	26	15	17
А2	10	15	20	40
А3	21	27	11	25

Решение:

3. Осуществляется первоначальное закрепление поставщиков за потребителями методом северо-западного угла (то есть с верхнего левого угла в правый нижний, см. План 1, в котором записаны исходные данные), а именно: поставщик А₁ может полностью удовлетворить потребности В₁ (15 единиц груза) и у него остается 5 единиц, которые он поставит В₂. На этом объем производства у А₁ закончен, а недостающие 14 единиц продукции В₂ получает от А₂, у которого еще остается 16 единиц (30 – 14), которые он отправит в пункт В₃ и так далее (План 1).
   

План 1

Вj Аi	В1	В2	В3	В4	Произ-водство
А1	22 15	26 5	15	17	20
А2	10	15 14	20 16	40	30
А3	21	27	11 12	25 33	45
Потреб-ность	15	19	28	33	95

4. Транспортные затраты по плану 1 составляют:
   

ТЗ₁ = 15 (22) + 5 (26) + 14 (15) + 16 (20) + 12 (11) + 33 (25) =

= 1947 ден. ед.

Проверка Плана 1 на оптимальность:

5. m + n – 1 = 3 + 4 – 1 = 6 данный критерий условно отвечает оптимальности;
   
6. исследование неиспользованных маршрутов (А₁В₃, А₁В₄, А₂В₁, А₂В₄, А₃В₁ и А₃В₂). Исследование осуществляют составлением транспортной цепи, которая составляется ходом шахматной ладьи по занятым пунктам и с возвратом в начальный. Предпочтительно цепочку вести по часовой стрелке (повороты делаются под прямым углом, минуя промежуточные пункты). Предполагается переброска груза в свободные пункты (+) и для сохранения баланса в следующем пункте эта величина груза вычитается (–). Так для А₁В₃ транспортная цепочка составит А₁В₃ (+)  А₂В₃ (–)  А₂В₂ (+)  А₁В₂ (–). Затраты по переброске в пункт А₁В₃ составят: З = 15 – 20 + 15 – 26 = – 16 ден.ед., что говорит о целесообразности такой переброске, ибо только на переброске одной единицы груза экономится 16 ед. транспортных затрат.
   

Для А₁В₄ (+)  А₃В₄ (–)  А₃В₃ (+)  А₂В₃ (–)  А₂В₂ (+)  А₁В₂ (–) =
= 17 – 25 + 11 – 20 + 15 – 26 = – 28 ден.ед., то есть имеется еще большая экономия.

Аналогичным образом осуществляется анализ остальных неиспользованных маршрутов;

7. после анализа всех неиспользованных маршрутов делается переброска в тот пункт, который дает наибольшую экономию транспортных затрат (наибольшее отрицательное число в транспортной цепи имеется в пунте А₁В₄, то есть – 28 ден.ед.);
   
8. переброска делается по цепи А₁В₄  А₃В₄  А₃В₃  А₂В₃  А₂В₂  А₁В₂  А₁В₄. Из всей цепи, для сохранения баланса выбирается минимальная величина груза (это 5 ед. в А₁В₂). Эта величина груза поставляется в пункт А₁В₄, а также в те пункты, которые получили положительные оценки (А₃В₃, А₂В₂), а из величин груза в пунктах с отрицательной оценкой (А₃В₄, А₂В₃ и А₁В₂) эти 5 ед. вычитаются.
   

План 2

Вj Аi	В1	В2	В3	В4	Производство
А1	22 15	26	15	17 5	20
А2	10	15 19	20 11	40	30
А3		27	11 17	25 28	45
Потребность	15	19	28	33	95