Учебное пособие йошкар-Ола, 2001 ббк у053 П815

Вид материала

Содержание

Методы, используемые в анализе
Xij на всех этапах транспортной задачи должно быть равным m + n –1

Подобный материал:

1 ... 9 10 11 12 13 14 15 16 17

5.2.1. Определение нормативной величины результативного
признака на основе корреляционного метода

Пример 36

В результате корреляционно-регрессионного анализа (КРА) по предприятиям объединения для каждого из них были получены зависимости рентабельности продукции от ряда факторов. Так для первого предприятия эта зависимость выражалась следующей моделью:

у_х = – 2,17 + 0,226х₁ + 0,0395х₂ – 0,0924х₃ + 0,064х₄.

Наименования факторов (х_i) и их числовые значения представлены в таблице 17, в которой дано определение расчетной рентабельности по предприятию № 1 объединения. Этот расчет является первым этапом расчета нормативной величины.

Таблица 17

Определение расчетной рентабельности по предприятию № 1

№ стр.	Фактор рентабельности	Коэффи-циент отдачи единицы фактора )	Среднее значение фактора в отчетном периоде	Расчетная рентабель-ность (гр. 3  гр. 4)
1	2	3	4	5
1.	Выработка, шт/чел. (х₁)	0,226	72	16,3
2.	Мощность на одного рабочего, квт (х₂)	0,0395	194	7,7
3.	Продолжительность одного оборота текущих активов (х₃)	– 0,0924	24,3	– 2,2
4.	Средний стаж квалифицированных рабочих основной профессии, лет (х₄)	0,064	31	2,0

Продолжение табл. 17

1	2	3	4	5
5.	Итого:			23,8
6.	Свободный член уравнения (а₀)			– 2,17
7.	Расчетная рентабельность (стр. 5 + стр.6), %			21,63
) Величина параметров уравнения при факторах (х_i)

Вторым этапом является определение прогрессивного уровня хозяйствования. Он определяется после того как для каждого предприятия будет найдена расчетная величина рентабельности, значения которой проставляются в графе 2 таблицы 18.

Таблица 18

Определение прогрессивного уровня хозяйствования

	Рентабельность	Уровень хозяйствования
№ предприятия	расчетная	фактическая	фактический (гр.3 : гр.2)  100, %	Средний прогрессивный (х_n)
1	2	3	4	5
1.	21,63	23,62	109,2	х_n = (109,2 + 104,8 + 111,8) : 3 = 108,6 % или 109 %
2.	18,07	17,05	94,4
3.	20,10	21,06	104,8
4.	19,9	17,9	90
5.	20,40	22,8	111,8
6.	18,9	15,91	84,2
–	19,7	19,7	100,0

Достижение среднего прогрессивного уровня хозяйствования предполагается достичь за два года по 50 % в каждом, то есть по 4,5 % в год (50 % от 9 %).

Третий этап предполагает выявление резервов улучшения использования факторов включенных в корреляционную модель. Предположим, что на предприятии были разработаны мероприятия организационного и технического характера, которые позволят улучшить показатели факторов х₁, х₂ и х₃ в предстоящем (плановом) периоде (см. гр.6 табл.19). Тогда с учетом их лучшего использования и прогрессивного уровня хозяйствования, расчет нормативной рентабельности может быть определен по схеме указанной в таблице 19.

Таблица 19

Расчет норматива рентабельности продукции на предприятии № 1

№ стр.	Фактор рентабельности	а_i	Уровень хозяйствования	Норма отдачи фактора (гр.3  гр.4)	Величина фактора в плановом периоде	Норматив (гр.5  гр. 6)
1	2	3	4	5	6	7
1.	х₁	0,226	1,045	0,236	75	17,71
2.	х₂	0,0395	1,045	0,0413	232	9,58
3.	х₃	– 0,0924	1,045	– 0,0965	23	– 2,22
4.	х₄	0,064	1,045	0,0679	31	2,10
5.	Итого:	х	х	х	х	27,17
6.	а₀	х	х	х	х	– 2,17
7.	Норматив рентабельности (стр.5 + стр.6)	х	х	х	х	25,00

Величина норматива рентабельности продукции при умеренной инфляции позволяет предприятию быть прибыльным. Еще большая гарантия быть доходным будет при увеличении норматива, что возможно при расчете его от фактически достигнутого уровня.

Нормативное значение рентабельности продукции может быть определено и на основе фактического уровня (23,62 %, см. табл.18, стр.1, гр.3), то есть расчет делается от фактически достигнутого уровня. При этом нормируются только приросты за счет увеличения ресурсов
в предстоящем периоде (см. табл.20).

Таблица 20

Определение норматива приростным методом

№ стр.	Фактор рентабельности	Величина фактора	Увеличение фактора	Норма отдачи	Рост рентабе-льности (гр.5  гр.6), %
		факт	план
1	2	3	4	5	6	7
1.	х₁	72	75	3	0,236	0,708
2.	х₂	194	232	38	0,0413	1,569

Продолжение табл. 20

1	2	3	4	5	6	7
3.	х₃	24,3	23	– 1,3	– 0,0965	0,125
4.	х₄	31	31	–	–	–
5.	Итого:	х	х	х	х	2,402
6.	Фактическая рентабельность, %	х	х	х	х	23,62
7.	Норматив рентабельности (стр.5 + стр.6), %	х	х	х	х	26,02

Расчет норматива приростным методом (от фактически достигнутого уровня) дает наибольшую величину и тем самым большую обеспеченность ведения прибыльного производства.

Аналогичным образом (или по первому способу) определяются нормативы по другим предприятиям отрасли региона.

5.2.2. Определение тесноты связи в рядах динамики на основе
метода корреляции

Пример 37

Имеются данные за девять лет о росте объема производства продукции А (Х_i) и цене единицы продукции (У_i) в процентах к 1980 год (1980 год принят за 100 %).

Требуется дать оценку связи между У и Х на основе коэффициента парной корреляции, значения которых представлены в таблице 21
в хронологическом порядке (1981, 1982, 1983 и т.д.).

Таблица 21

Динамика производства и цены единицы продукции (1980 год = 100 %)

у	х	ух	у²	х²
93 101 109 100 108 111 98 99 99	114 97 100 105 111 112 117 121 124	10602 9797 10900 10500 11655 12432 11466 11979 12276	8649 10901 11881 10000 11025 12321 9604 9801 9801	12996 9409 10000 11025 12321 12544 13682 14641 15376
 915	1001	101607	93283	112001

Решение:

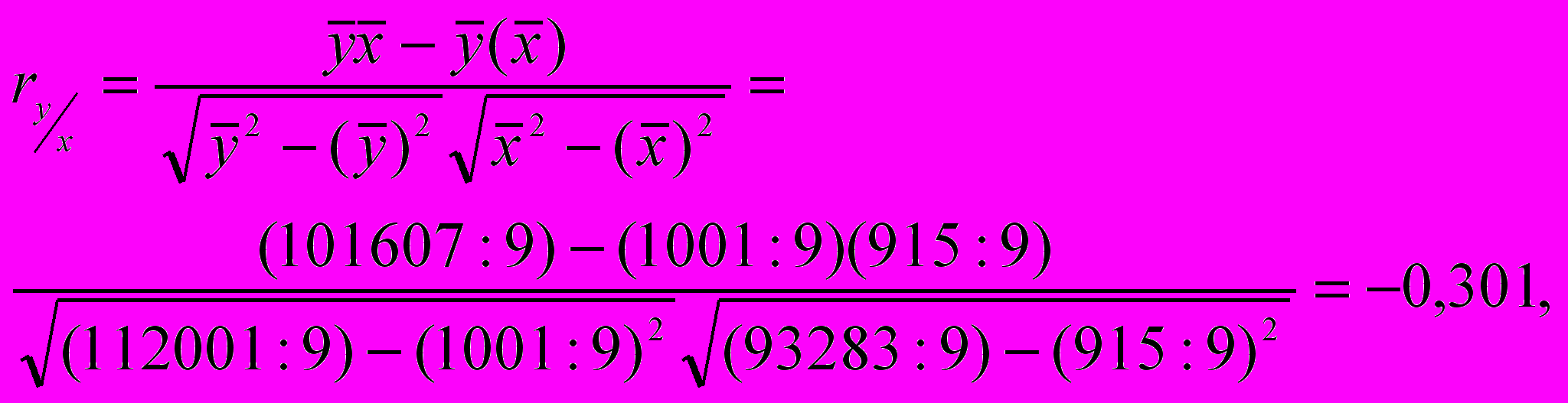
то есть связь обратная и слабая.

Проверка на автокорреляцию осуществляется по каждому признаку путем сдвига в годах и коррелирования уровня 1991 г. с 1992 г., 1992 г. с 1993 г. и т.д. (см. табл.22, которая приводится частично, остальные значения рекомендуется студентам сделать самостоятельно).

Таблица 22

Расчетная таблица на оценку автокорреляции
по динамике объема продукции

х	х₁	х²	х₁²	хх₁
114 97 100 … 121	97 100 105 … 124	12996 9409 10000 … 14641	9409 10000 11025 … 15376	11058 9700 … 15004
 877	887	96625	99005	97610

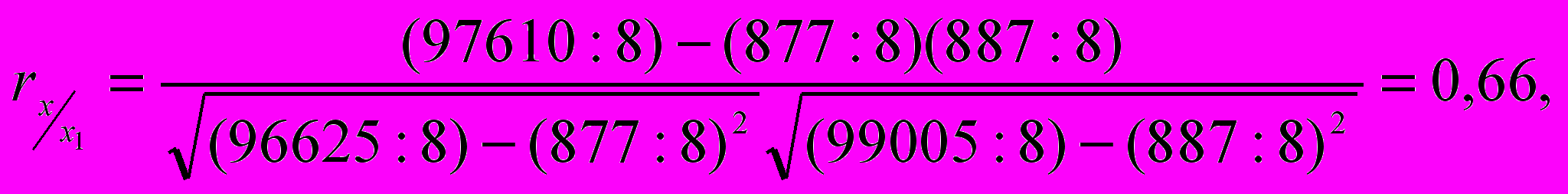
что больше 0,5 и говорит о существенности связи между смежными годами, то есть имеется автокорреляция.

Аналогично расчет делается по ценам (см. табл.23).

Таблица 23

Расчетная таблица на оценку автокорреляции
по динамике цены на единицу продукции

у	у₁	у²	у₁²	уу₁
93	101	8649	10201	9393
101	109	10201	11881	11009
109	100	11881	10000	10900
…	…	…	…	…
99	99	9801	9801	9801
 816	822	83482	84634	83838

.

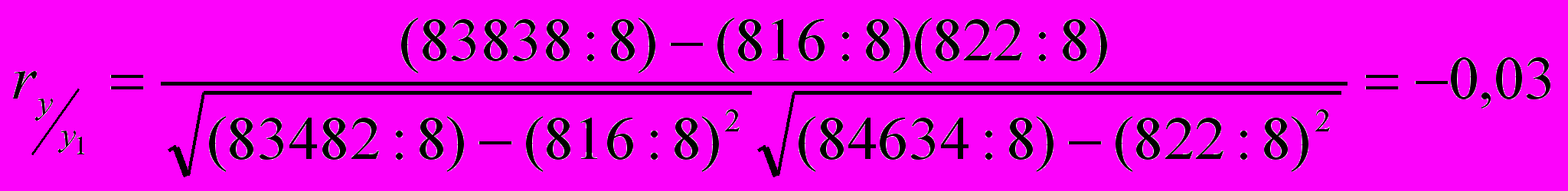Для исключения автокорреляции по обоим рядам динамики таблицы 21 определяются тренды (х_i), то есть их теоретические значения путем сглаживания. В качестве линии выравнивания применяется уравнение прямой линии (см. табл.24 и 25).

Таблица 24

Выравнивание динамики производства продукции

Годы (t)	х	хt	t²	х_i = а₀ + а₁t = 98,47 + 2,55 t	Отклонения (гр.2 – гр.5)
1	2	3	4	5	6
1	114	114	1	101	13
2	97	194	4	103,6	– 6,6
3	100	300	9	106,1	– 6,1
4 5 6 7 8 9	105 111 112 117 121 124	420 555 672 819 968 1116	16 25 36 49 64 81	108,7 111,2 113,8 116,3 118,9 121,4	– 3,7 – 0,2 – 1,8 0,7 2,1 2,6
 45	1001	5158	285	1001	х

Параметры уравнения х = а₀ + а₁t определяются из системы уравнений

,
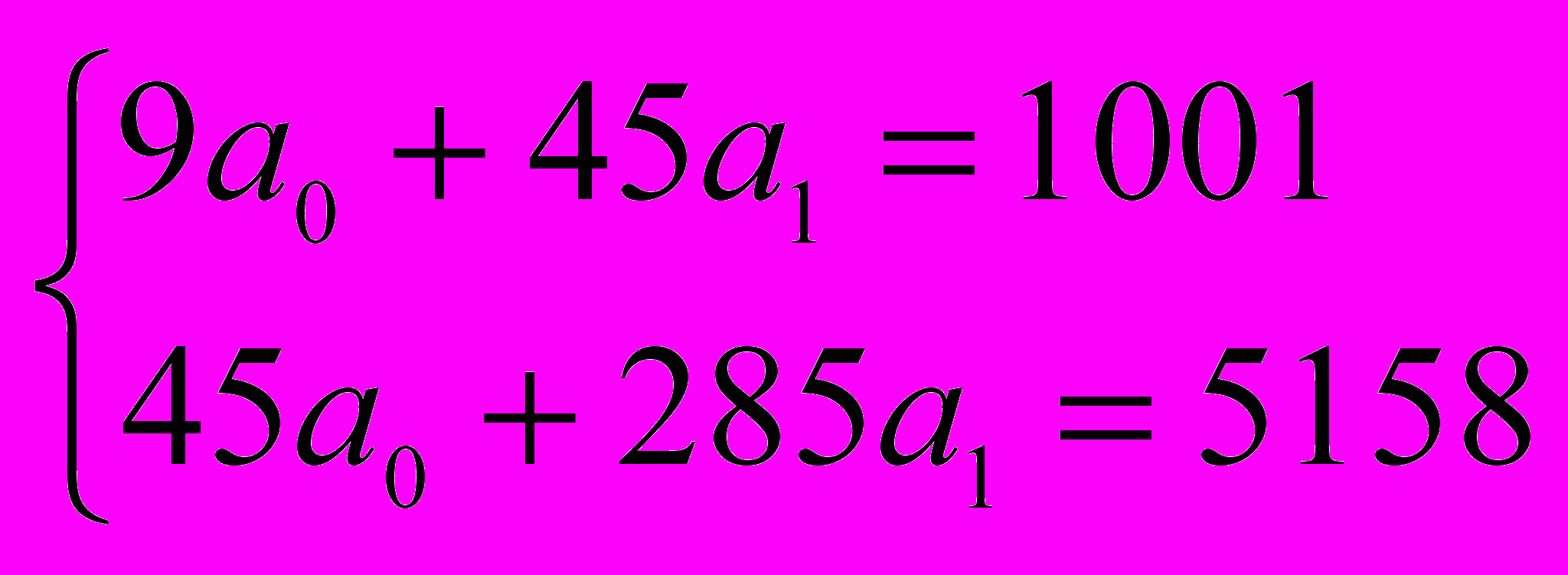
откуда

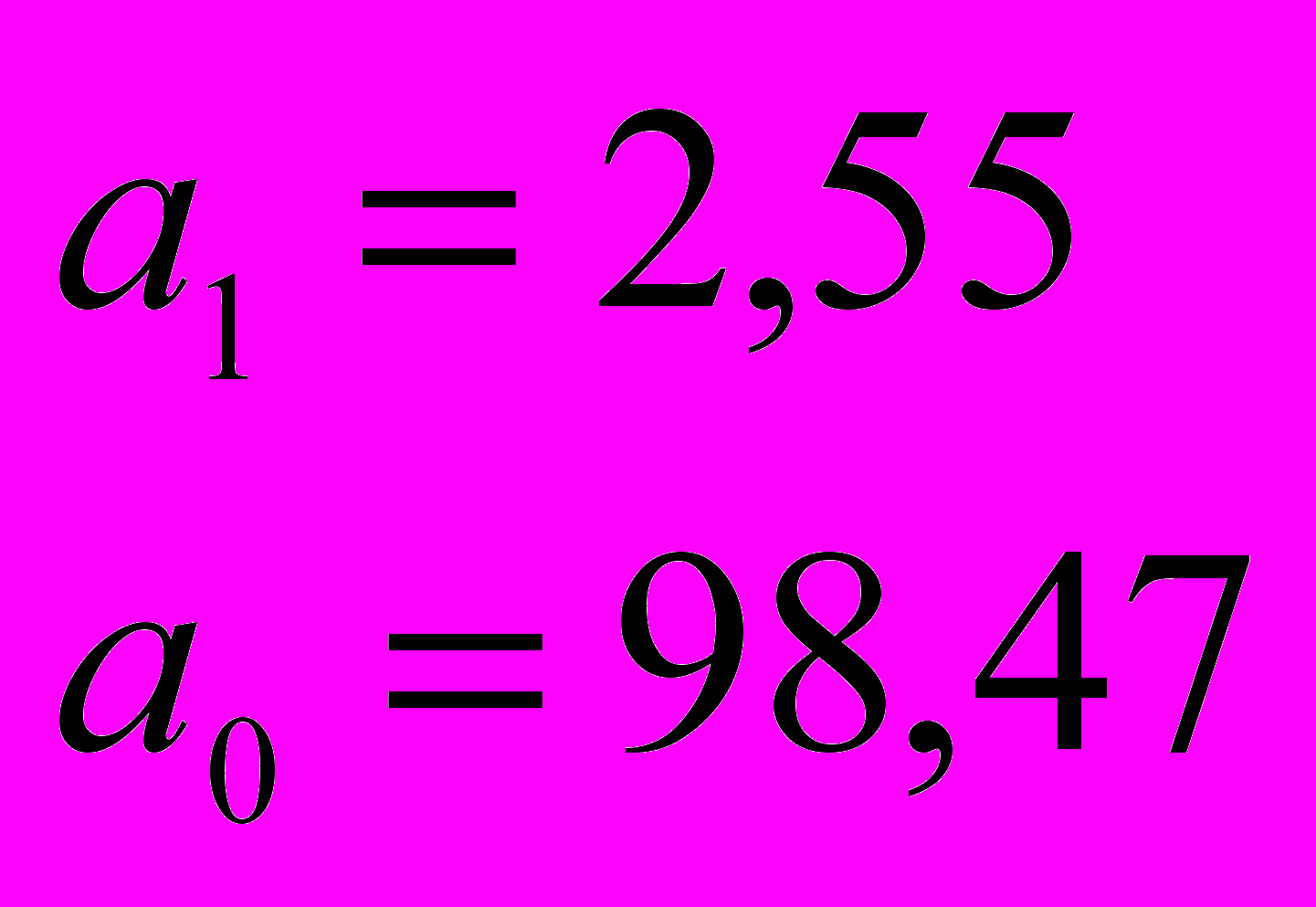
то есть линия выравнивания (сглаживания ряда динамики) выражается математической моделью

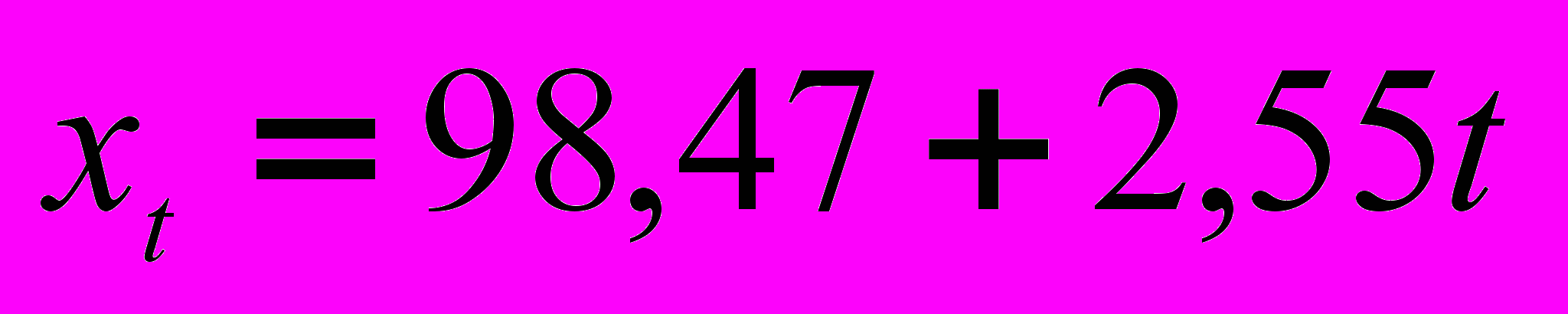, подставляя значения t (1,2,3, …,9), получаются теоретические значения, которые представлены в графе 5 таблицы 24.

Аналогичным образом осуществляется сглаживание ряда динамики цены единицы продукции (см. табл.25)

Таблица 25

Выравнивание динамики цены единицы продукции

Годы (t)	у	уt	t²	у_t = а_о+ а₁t = 101,082 + + 0,117t	Отклонение (гр.2 – гр.5)
1	2	3	4	5	6
1	93	93	1	101,2	– 8,2
2	101	202	4	101,3	– 0,3
3	109	327	9	101,4	7,6
4	100	400	16	101,6	– 1,6
5	105	525	25	101,7	3,3

Продолжение табл. 25

1	2	3	4	5	6
6	111	666	36	101,8	9,2
7	98	686	49	101,7	– 3,2
8	99	792	64	102,0	– 3,0
9	99	891	81	102,1	– 3,1
45	915	4582	285	915,0	х

Параметры уравнения у_t = а_о + а₁t определяются из системы уравнений

,
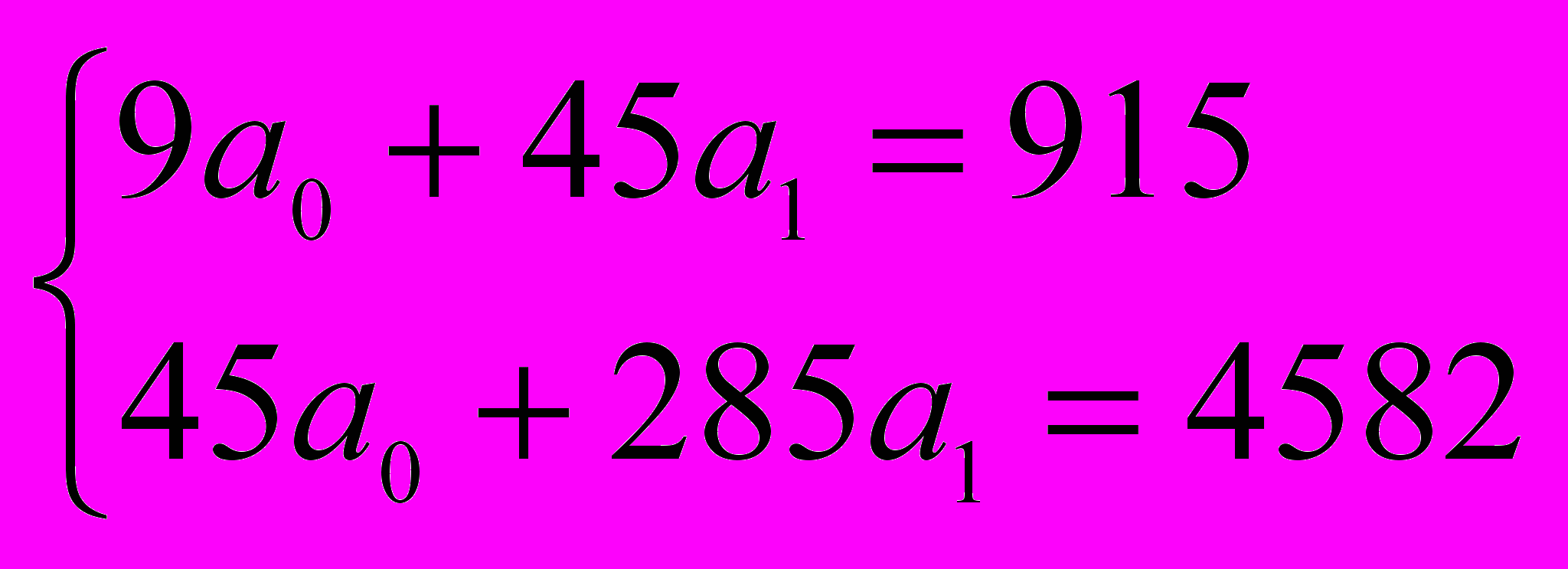
откуда

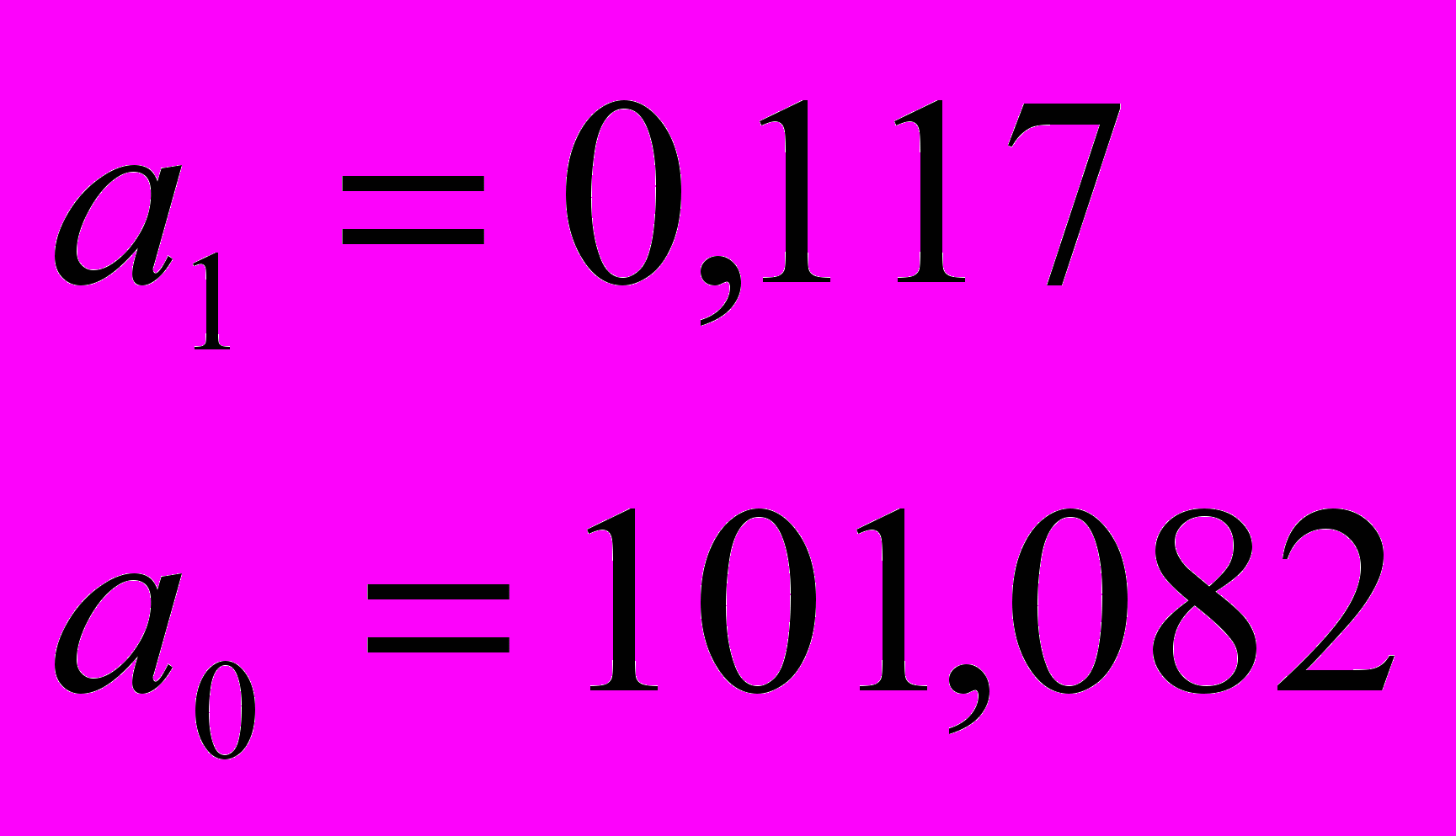
то есть линия выравнивания (сглаживание ряда динамики) выражается математической моделью у_t = 101,082 + 0,117 t. Подставляя значения t (1, 2, 3,…, 9), получаются теоретические значения, которые представлены в графе 5 таблицы 24.

Последним вычислительным действием является коррелирование отклонений фактических (эмперических) данных от теоретических по обоим признакам (см. табл.26).

Таблица 26

Определение тесноты связи между У и Х по отклонениям
фактических данных от теоретических

Отклонение по	∆х  ∆у	d²х	d²у
продукции ∆х	ценам ∆у
13,0	– 8,2	– 106,60	16900	67,24
– 6,6	– 0,3	1,98	43,56	0,09
– 6,1	7,6	– 46,36	37,21	57,76
– 3,7	– 1,6	5,92	13,69	2,56
– 0,2	3,3	– 0,66	0,04	10,89
– 1,8	9,2	– 16,56	3,24	84,64
0,7	– 3,9	– 2,73	0,49	15,21
2,1	– 3,0	– 6,30	4,41	9,00
2,6	– 3,1	– 8,06	6,76	9,61
		– 179,37	– 278,40	257,00

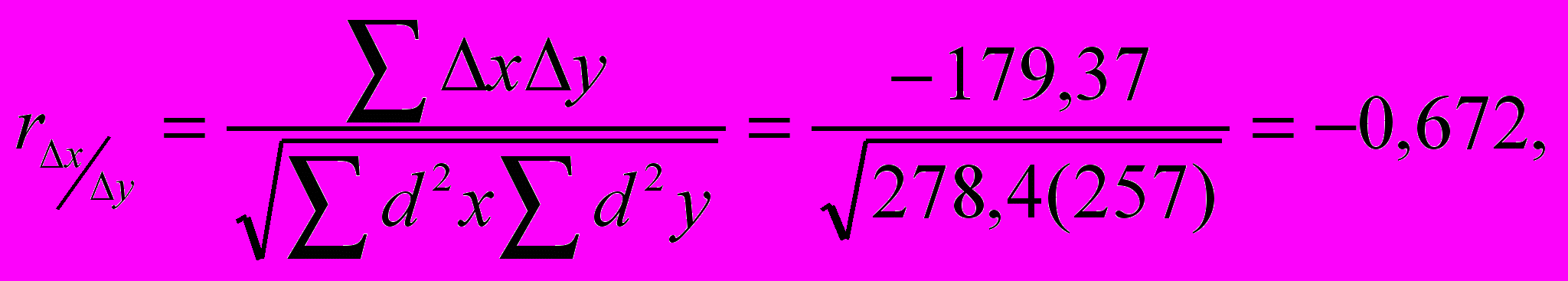
что говорит о тесной и обратной связи между У и Х и соответствует фактической силе и направленности в условиях рыночных отношений.

ТЕМА 6

ЭКОНОМИКО-МАТЕМАТИЧЕСКИЕ
МЕТОДЫ, ИСПОЛЬЗУЕМЫЕ В АНАЛИЗЕ

Транспортные задачи

Важнейшим инструментом экономического анализа является математическое моделирование экономических явлений и процессов.
В экономическом анализе в основном используются математические модели, которые описывают изучаемые явления и процессы в виде неравенств, уравнений и других математических функций.

Наибольшее распространение из экономико-математических методов (ЭММ) в практике экономического анализа получили методы линейного программирования, в частности при решении транспортных
и производственных задач. Так математическая формулировка траспортной задачи состоит в следующем:

имеется m – поставщиков и n – потребителей.

Количество продукции у поставщика i-го составляет – Ai, спрос потребителя j – Bj.

Затраты по перевозке одной машины груза от i-го поставщика к j – му потребителю составляет – Cij : ( Cij  0).

Размер поставки от i к j составляет Xij.

Исходные данные должны удовлетворять следующему условию: наличие продукции у поставщика равно потребностям потребителей
(в случаях их неравенства вводится фиктивный поставщик или потребитель).

.

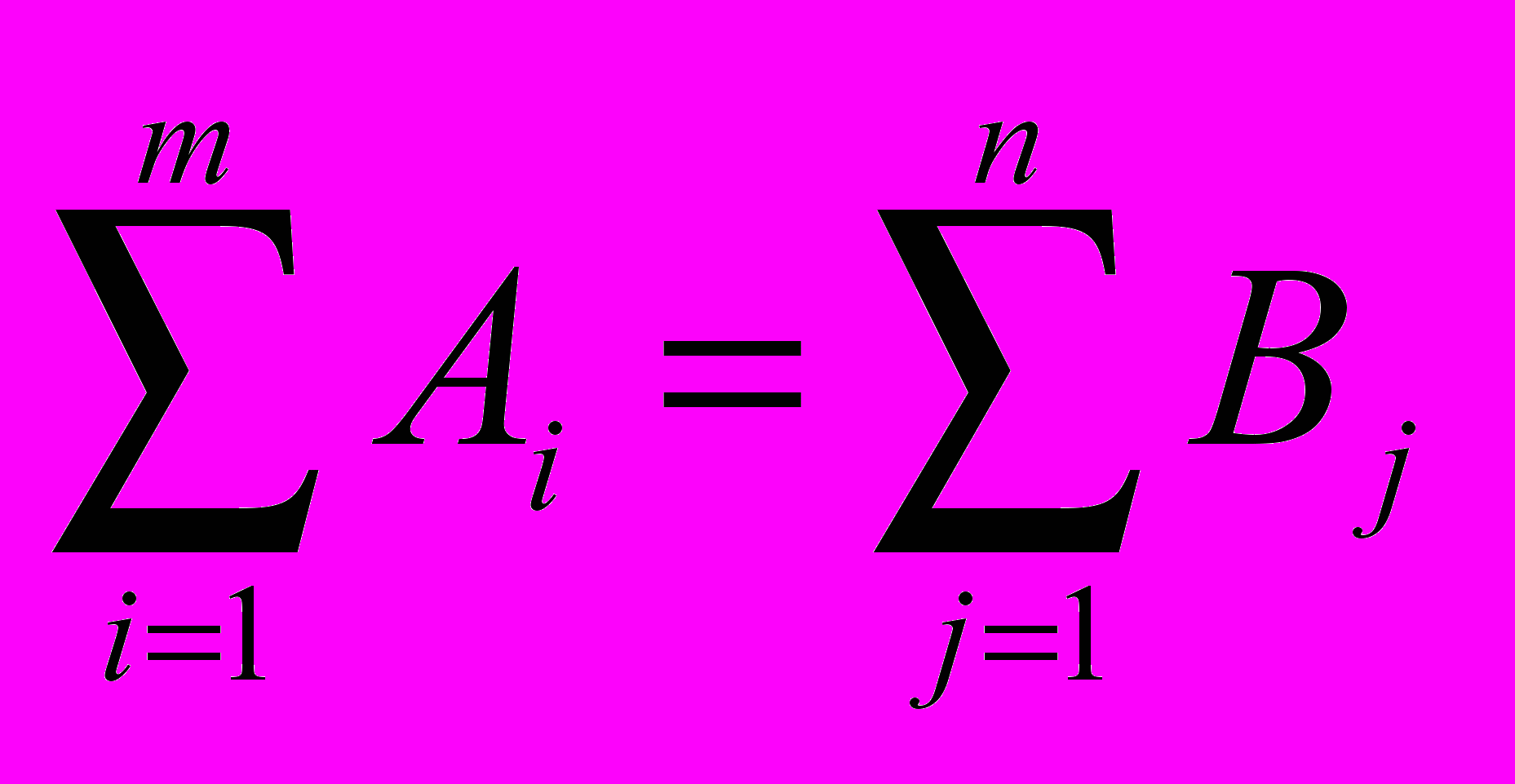Исходное решение отвечает следующей целевой функции:

,

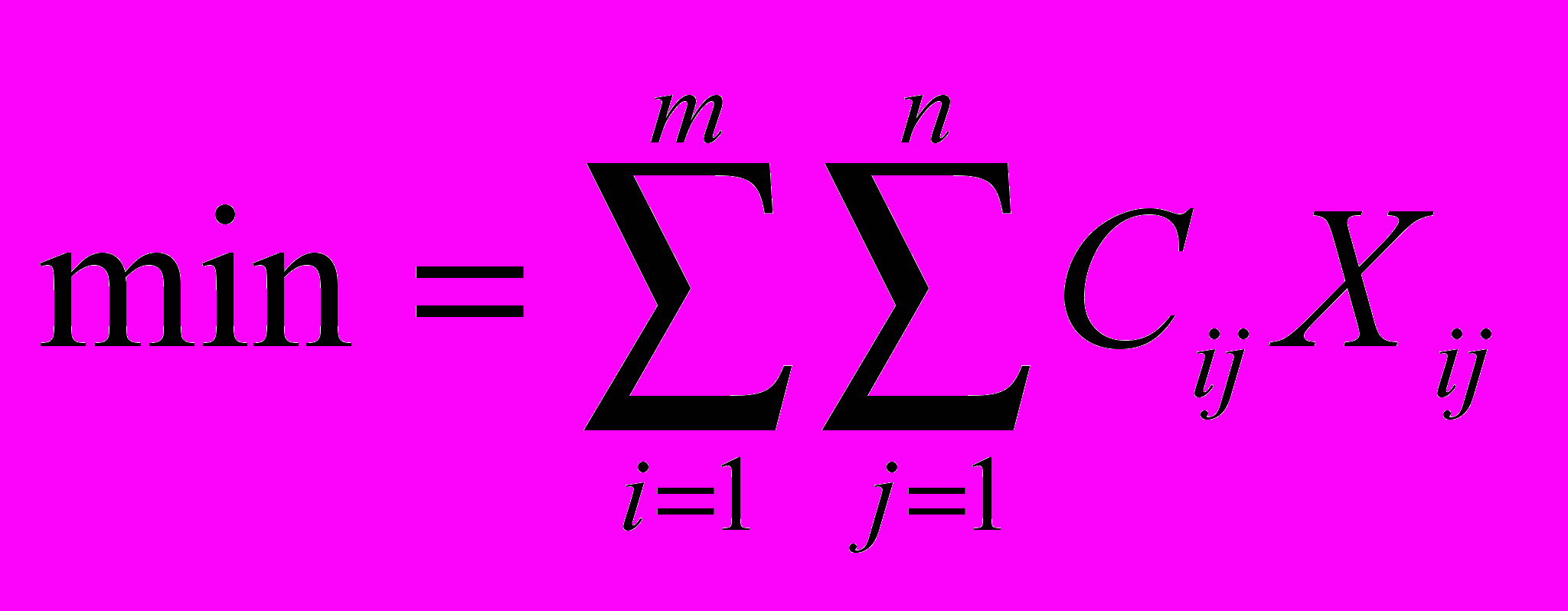то есть затраты по перевозкам должны быть минимальными.

Необходимо отметить, что количество неизвестных Xij на всех этапах транспортной задачи должно быть равным m + n –1, то есть число неиспользованных маршрутов отвечает данной величине. Это и будет первым критерием оптимальности.

Пример 38

Имеется три склада, расположенные в трех пунктах: А₁, А₂, А₃.
В пункте А₁ имеется 20 машин груза, в пункте А₂ – 30, в пункте А₃ – 45 машин груза.

Этот груз должен быть доставлен в четыре пункта назначения В₁, В₂, В₃ и В₄. Причем пункту В₁ необходимо доставить 15 машин груза, В₂ – 19, В₃ – 28 и пункту В₄ – 33 машины груза.

Затраты в денежных (ден.) единицах (ед.) на перевозку одной машины из пункта А_i в пункт B_j представлены в следующей таблице:

Таблица 27

Контрагенты	Потребители
В₁	В₂	В₃	В₄
Постав-щики	А₁	22	26	15	17
А₂	10	15	20	40
А₃	21	27	11	25

Решение:

Осуществляется первоначальное закрепление поставщиков за потребителями методом северо-западного угла (то есть с верхнего левого угла в правый нижний, см. План 1, в котором записаны исходные данные), а именно: поставщик А₁ может полностью удовлетворить потребности В₁(15 единиц груза) и у него остается 5 единиц, которые он поставит В₂. На этом объем производства у А₁ закончен, а недостающие 14 единиц продукции В₂ получает от А₂, у которого еще остается 16 единиц (30 – 14), которые он отправит в пункт В₃ и так далее (План 1).

План 1

Вj Аi	В₁	В₂	В₃	В₄	Произ-водство
А₁	22 15	26 5	15	17	20
А₂	10	15 14	20 16	40	30
А₃	21	27	11 12	25 33	45
Потреб-ность	15	19	28	33	95

Транспортные затраты по плану 1 составляют:

ТЗ₁ = 15 (22) + 5 (26) + 14 (15) + 16 (20) + 12 (11) + 33 (25) =

= 1947 ден. ед.

Проверка Плана 1 на оптимальность:

m + n – 1 = 3 + 4 – 1 = 6 данный критерий условно отвечает оптимальности;
исследование неиспользованных маршрутов (А₁В₃, А₁В₄, А₂В₁, А₂В₄, А₃В₁ и А₃В₂). Исследование осуществляют составлением транспортной цепи, которая составляется ходом шахматной ладьи по занятым пунктам и с возвратом в начальный. Предпочтительно цепочку вести по часовой стрелке (повороты делаются под прямым углом, минуя промежуточные пункты). Предполагается переброска груза в свободные пункты (+) и для сохранения баланса в следующем пункте эта величина груза вычитается (–). Так для А₁В₃транспортная цепочка составит А₁В₃ (+)  А₂В₃ (–)  А₂В₂ (+)  А₁В₂ (–). Затраты по переброске в пункт А₁В₃ составят: З = 15 – 20 + 15 – 26 = – 16 ден.ед., что говорит о целесообразности такой переброске, ибо только на переброске одной единицы груза экономится 16 ед. транспортных затрат.

Для А₁В₄ (+)  А₃В₄ (–)  А₃В₃ (+)  А₂В₃ (–)  А₂В₂ (+)  А₁В₂ (–) =
= 17 – 25 + 11 – 20 + 15 – 26 = – 28 ден.ед., то есть имеется еще большая экономия.

Аналогичным образом осуществляется анализ остальных неиспользованных маршрутов;

после анализа всех неиспользованных маршрутов делается переброска в тот пункт, который дает наибольшую экономию транспортных затрат (наибольшее отрицательное число в транспортной цепи имеется в пунте А₁В₄, то есть – 28 ден.ед.);
переброска делается по цепи А₁В₄  А₃В₄  А₃В₃  А₂В₃ А₂В₂  А₁В₂  А₁В₄. Из всей цепи, для сохранения баланса выбирается минимальная величина груза (это 5 ед. в А₁В₂). Эта величина груза поставляется в пункт А₁В₄, а также в те пункты, которые получили положительные оценки (А₃В₃, А₂В₂), а из величин груза в пунктах с отрицательной оценкой (А₃В₄, А₂В₃ и А₁В₂) эти 5 ед. вычитаются.

План 2

Вj Аi	В₁	В₂	В₃	В₄	Производство
А₁	22 15	26	15	17 5	20
А₂	10	15 19	20 11	40	30
А₃		27	11 17	25 28	45
Потребность	15	19	28	33	95

Blog

Учебное пособие йошкар-Ола, 2001 ббк у053 П815

Содержание