Задача минимизации длин проводников 21

Вид материала

Задача

Содержание 3.4Тестирование и метрики Название ячейки Включено с низким приоритетом Приложение Технологические правила Рис. 33 Простые технологические правила Правила для повышения выхода годных Список литературы

Подобный материал:

• С. В. Шешенин 1/2 года  Классические краевые задачи линейной теории упругости в перемещениях., 13.12kb.
• Методы улучшения сходимости алгоритма минимизации функционала, ассоциированного с задачей, 103.65kb.
• О минимизации признакового пространства в задачах распознавания Ветров Д. П., Рязанов, 59.25kb.
• К. П. Ивкин московский инженерно-физический институт (государственный университет), 26.94kb.
• Автоматизированное проектирование схем размещения объектов предприятий из условия минимизации, 124.49kb.
• Проводников в виде участков металлизированного покрытия, размещенных на диэлектрическом, 34.38kb.
• Единый социальный налог: анализ типичных схем минимизации налога, применяемых организациями, 193.29kb.
• Взависимости от числа нанесенных печатных проводников на платы, они разделяются на:, 20.37kb.
• Программа курса лекций «Математические методы и модели исследования операций», 27.98kb.
• Т. М. Боровська кандидат технічних наук, доцент І. С. Колесник, 118.17kb.

3.4Тестирование и метрики

Первая метрика – время, т.е. сколько времени понадобиться графовому методу, чтобы найти решения, удовлетворяющие функции минимизации длин проводников (без сохранения конфигурации) или функции минимизации изменений в топологии (с сохранением конфигурации). Точность метрики составляет десятые доли минут. Ячейки содержат до 3 десятков транзисторов.

№	Название ячейки	Кол-во транзисторов.	Без сохранения конфигурации	С сохранением конфигурации
Длительность (мин.)	Размерность графа (В/Р)	Длительность (мин.)	Размерность графа (В/Р)
1	adfullm_1	34	0.2	538/2636	0.3	1019/3976
2	and2_8	18	<0.1	348/1488	0.1	609/2206
3	aoi222_4	36	0.3	452/2210	0.5	831/3266
4	aoi331_4	36	1	478/2310	1	908/3496
5	muxi4_4	32	0.5	568/2781	0.8	1064/4151
	Общее время:	-	2.0	-	2.7
	Среднее время:	-	0.400	-	0.504

Тест показал, что задача миграции с сохранением конфигурации чувствительна к размерности графа. Увеличение размерности задачи c приведенными нами выше методами уменьшения, увеличивает время работы алгоритма до 30% по сравнению с миграцией без сохранения конфигурации.

Следующая метрика – это количество, выравненных сток/исток контактов между двумя затворами.

№	Название ячейки	Количество контактов для выравнивания	Выравнивание сток/исток контактов
Выключено	С низким приоритетом	С высоким приоритетом
1	adfullm_1	30	24	25	26
2	and2_8	27	27	27	27
3	aoi222_4	29	27	28	29
4	aoi331_4	22	19	19	22
5	muxi4_4	29	17	17	20

При выключенной опции, указано количество контактов, которые не нуждается в выравнивании. Выравнивание с низким приоритетом позволяет выровнять несколько контактов, а с высокими – до всех.

Следующая метрика – это количество контактов, центрированных внутри фигур топологии. Указано количество центрированных контактов как в одной верхней или нижней топологической фигуре, так и в обеих.

№	Название ячейки	Количество контактов для выравнивания	Центрирование контактов в металлических и поликремневых участках цепей
Выключено	Включено с низким приоритетом	Включено с высоким приоритетом
В одном контуре	В обоих контурах	В одном контуре	В обоих контурах	В одном контуре	В обоих контурах
1	adfullm_1	63	37	6	39	6	41	10
2	and2_8	43	26	2	28	2	28	3
3	aoi222_4	59	31	9	31	9	35	12
4	aoi331_4	54	31	6	31	7	31	9
5	muxi4_4	68	36	12	36	14	41	17

3.5Выводы

В данной главе рассмотрен формальный алгоритм работы системы миграции, основанной на графе ограничений. Представлена UML диаграмма класса Minimizer. Указан обзор каждого этапа процесса миграции. Приведен пример выходной топологии с учетом минимизации длин проводов (без сохранения конфигурации) и минимизации изменений.

Кроме того приведены метрики показывающие эффективность графового метода над симплекс-методом, как в задаче минимизации длин проводов, так и в задаче минимизации изменений. С помощью тестов удалось определить, что графовый метод нахождения минимума очень чувствителен к количеству дополнительных вершин. Решение задачи минимизации изменений с дополнительными переменными и неравенствами увеличивает длительность работы алгоритма до 30 %. Представлены метрики по выравниванию контактов, которые иллюстрируют эффективность предложенного подхода.

Заключение

Настоящая диссертационная работа посвящена исследованию проблемы миграции топологии стандартных ячеек СБИС с минимизацией изменений между исходной и целевой топологиями.

1. В работе проанализирован маршрут миграции на основе алгоритмов сжатия с использованием графа ограничений. Также проанализированы существующие целевые функции минимизирующие изменения топологии и указаны их недостатки.
   
2. Предложена целевая функция, которая позволяет минимизировать изменения, на основе которой построен подход для сохранения конфигурации всей топологии СЯ при миграции. Подход основан на минимизации изменений длин ребер двух из трех типов и ширин, которые можно получить согласно диаграммам Вороного для полигонов.
   
3. Предложен подход для выравнивания контактов в СЯ с использованием целевой функции.
   
4. Создана программная реализация данной функции минимизации и всего подхода в целом. Подход позволяет:
   
   1. автоматизировать процесс миграции топологии СЯ с сохранением конфигурации тем самым свести к минимуму работу дизайнеров по адаптации топологий СЯ к новым требованиям технологического процесса или архитектуры;
      
   2. в автоматическом режиме выравнивать контакты, сохраняя при этом конфигурацию топологии СЯ;
      
5. На основе проведенных тестов видно, что алгоритм миграции с сохранением конфигурации работает до 30% дольше, чем без сохранения конфигурации, при этом можно добиться выравнивания всех контактов в топологии СЯ
   

Приложение

Технологические правила

Технологические правила - это ограничения, накладываемые на геометрическую форму и размеры топологии ИС. Выполнение данных ограничений гарантирует, что схема может быть сделана с приемлемым выходом годных. Эти ограничения предотвращают короткие замыкания, разрывы проводников и выгорание межслойных переходов. Величины технологических правил обычно являются компромиссом между плотностью топологии и надежностью производства.

Технологические правила накладывают ограничения как на одну фигуру, так и между несколькими. К ограничениям для одной фигуры относятся минимальный размер и площадь. Между двумя фигурами можно ограничить минимальное расстояние, перекрытие, нависание и включение. Также существуют ограничения на максимальный размер, расстояние и требование постоянного размера. (Рис 38)



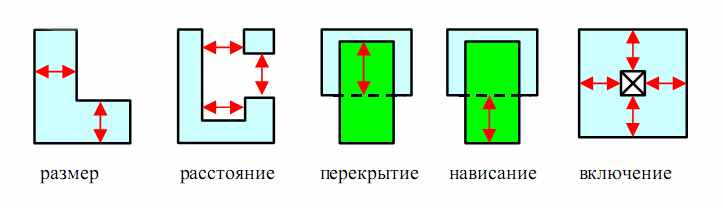
Рис. 33 Простые технологические правила

В простейшем случае все перечисленные выше типы правил накладывают ограничения на одну фигуру или пару фигур, и их величина постоянна. Однако, современные технологии и постоянное повышение степени интеграции приводят к тому, что величина правила становятся зависимой от следующих факторов:

• размера фигур (длины, ширины или площади Рис. 39);
  
• взаимного расположения (длины пересечения проекций Рис. 40а))
  
• количества соседей (Рис. 40б))
  
• присутствия другого объекта между ними (Рис. 40в)).
  

Поддержка таких правил существенно усложняет алгоритмы сжатия.



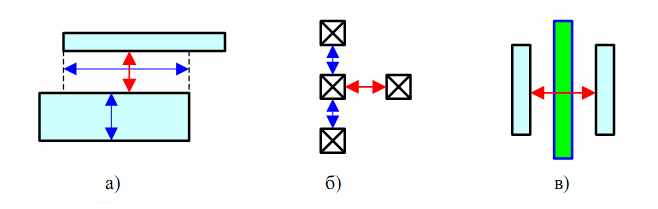
Рис. 34 Условные технологические правила

Правила для повышения выхода годных

На завершающей стадии топологического проектирования в уже готовую топологию добавляют дополнительные правила, выполнение которых повышает выход годных (DFM – Design For Manufacturability правила). О важности учета этих правил говорит тот факт, что только 1% снижения выхода годных при изготовлении СБИС на 300мм кремниевых пластинах приводит к дополнительным затратам на одной фабрике производителя в размере 5 млн. долларов в год [8].

Один из широко применяемых методов уменьшения числа систематических дефектов опирается на применение специальных DFM правил, которым присвоены приоритеты[9]. DFM правила можно разделить на две группы:

• обычные технологические правила, величина которых увеличена на 10-30%. К ним относятся увеличенные правила минимального размера, расстояния, включения, нависания, площади и т.д.
  
• правила, которые требуют наличия дополнительных (дублирующих) объектов в топологии, например, дополнительных межслойных переходов.
  

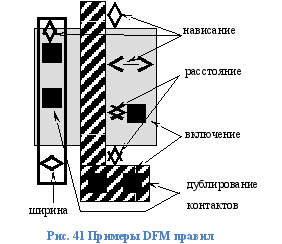
Примеры DFM правил приведены на Рис. 41.

Список литературы

1. Sherwani N. Algorithm for the VLSI Physical Design Automation. Second Edition. - Kluwer Academic Publishers, 1995. – 538 p.
   
2. М.А. Сотников, Алгоритм сжатия топологии стандартных ячеек субмикронных СБИС // Тр. НИИР. - 2002.- C. 108-112.
   
3. Juanwen Zhu, Frang Fang, Qianying Tang Calligrapher: A new Layout-Migration Engine for Hard Intellectual Property Libraries. IEEE Transactions on Computer-aided design of integrated circuits and system (September 2005 Volume 24 Number 9) ISSN 0278-0070
   
4. А.А. Корбут Ю.Ю.Финкельштейн под редакцией Д.Б. Юдина «Дискретное программирование» Москва 1969г.
   
5. А.С. Плеханов Метод минимизации задержек сигналов при сжатии топологии с учетом технологической сетки
   
6. Sching L.Lin Jonathan Allen. Minplex – A compactor that minimizes the boundary rectangle and individual rectangles in a layout. //Proceeding of the 23^rd Design Automation Conference 1986, pp123-130
   
7. Virtuoso Compactor Reference Manual, Product Version 5.0 ссылка скрыта
   
8. Jeff Wilson, Walter Ng, Via Doubling to Improve Yield // Mentor White Paper, August 2005
   
9. M.A.Сотников, Э.А.Улуханов, К.С.Муханов, //Улучшение топологии стандартных ячеек субмикронных СБИС для повышения выхода годных
   
10. F.-L. Heng, Z. Chen, and G.E. Tellez. “A VSLI artwork legalization technique based on a new criterion of minimum layout perturbation.” in Proc. Int Symp. Physical Design (ISPD), Napa Valley, CA. 1997 (pp 116-121)
    
11. К.С. Муханов, М.А. Сотников Алгоритм построения диаграммы Вороного для внутренней части замкнутого ортогонального полигона. // МЭС-2006.