Задача минимизации длин проводников 21
| Вид материала | Задача |
Содержание1.6Задача минимизации длин проводников 1.7Целевые функции, минимизирующие изменения топологии. Рис. 14 Миграция с использованием функции (6) Рис. 15 Миграция с использованием функции (9) |
- С. В. Шешенин 1/2 года Классические краевые задачи линейной теории упругости в перемещениях., 13.12kb.
- Методы улучшения сходимости алгоритма минимизации функционала, ассоциированного с задачей, 103.65kb.
- О минимизации признакового пространства в задачах распознавания Ветров Д. П., Рязанов, 59.25kb.
- К. П. Ивкин московский инженерно-физический институт (государственный университет), 26.94kb.
- Автоматизированное проектирование схем размещения объектов предприятий из условия минимизации, 124.49kb.
- Проводников в виде участков металлизированного покрытия, размещенных на диэлектрическом, 34.38kb.
- Единый социальный налог: анализ типичных схем минимизации налога, применяемых организациями, 193.29kb.
- Взависимости от числа нанесенных печатных проводников на платы, они разделяются на:, 20.37kb.
- Программа курса лекций «Математические методы и модели исследования операций», 27.98kb.
- Т. М. Боровська кандидат технічних наук, доцент І. С. Колесник, 118.17kb.
1.6Задача минимизации длин проводников
Данная задача сводиться к тому, что на выходе нужно получить топологический шаблон с минимальными длинами проводников, т.е. результатом оптимизации на сжатой топологии является уже топология, у которой все контакты соединены проводниками, а сумма длин всех проводников является минимально возможной при данном расположении контактных окон.
Целевая функция минимизации представлена в таком виде:
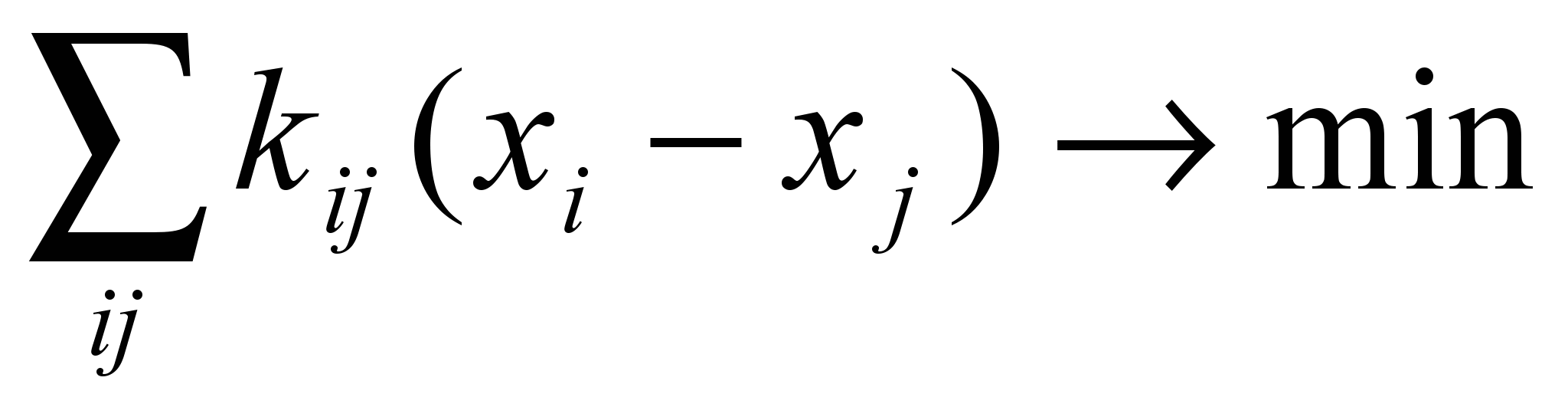 , если раскрыть скобки, то можно привести к виду
, если раскрыть скобки, то можно привести к виду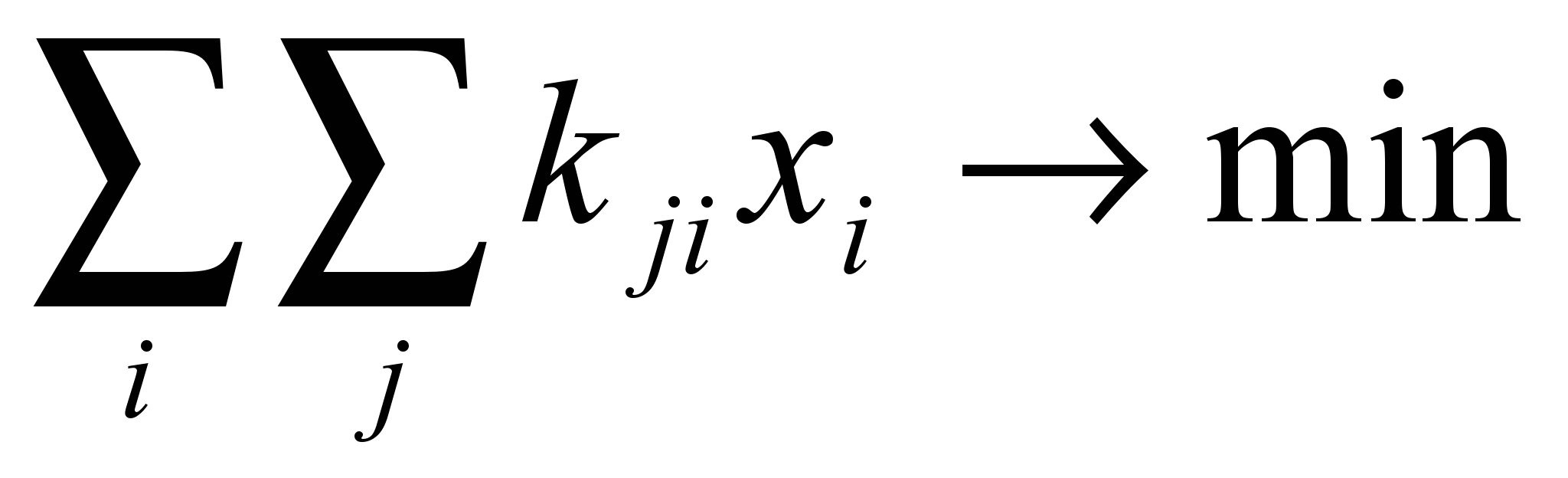 . На рисунке это выглядит так:
. На рисунке это выглядит так: 
Здесь xi и xj – это координаты края проводника в направлении x, а wi и wj - это соответствующие ширины. Коэффициенты k могут быть представлены как сопротивления проводника в данном месте и вычисляются как ортогональный размер, обозначенный стрелками, умноженный на сопротивление удельной длины материала данного слоя.
В САПР Cadence Virtuoso Compactor [7] коэффициенты ki берутся из специального технологического файла. Данные коэффициенты называются весами. Этот метод минимизации проводной длины определяется, как “взвешенная минимизация". Чем выше вес для объектов слоя, тем больше приоритет система сжатия дает для уменьшения длины проводов на том слое. Если никакие веса на заданы, то используется веса по умолчанию. В CMOS библиотеке по умолчанию веса для диффузионного слоя больше, чем веса для слоя поликремния, который в свою очередь больше, чем веса для металлических слоев. Объяснить это можно тем, что сопротивление слоя диффузии больше, чем поликремния, который в свою очередь больше, чем сопротивление металлических слоев. Система сжатия выполняет минимизацию длин проводов уже после сжатия топологии, используя эвристический алгоритм.
1.7Целевые функции, минимизирующие изменения топологии.
Для того чтобы перенести структуру топологии с минимальными изменениями на новый технологический процесс необходимо подобрать целевую функцию, минимизирующую изменения между входной топологией и выходной. Насколько точно перенесена исходная конфигурация топологии на целевую технологию, напрямую зависит от того, как точно задана целевая функция минимизации изменений.
В статье [10] указана целевая функция, которая минимизирует расстояние, между старым значением координаты объекта топологии и новым. Данная функция фигурирует под названием MP (Minimum perturbations). Имеет вид:
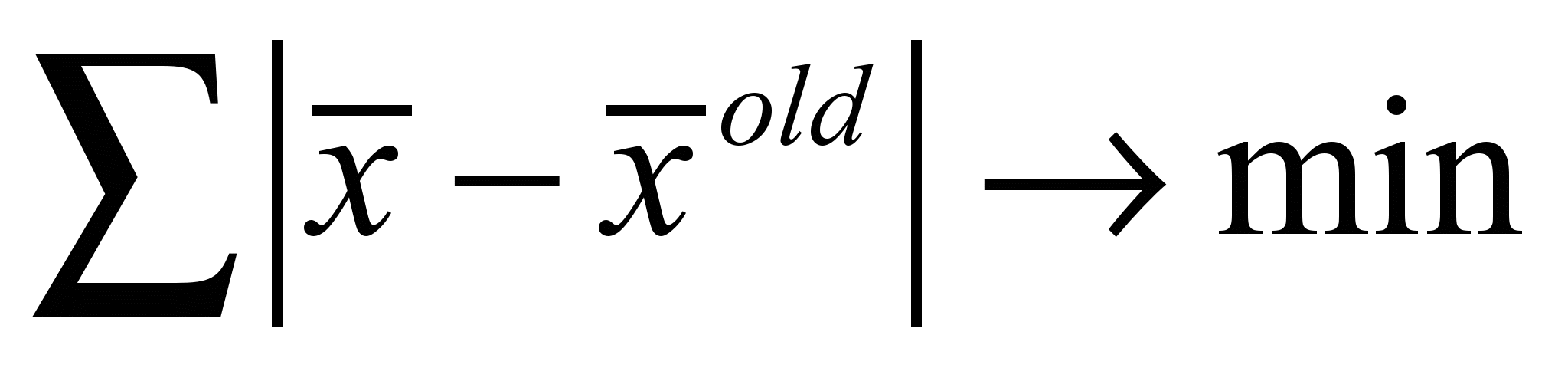 , (6)
, (6)здесь
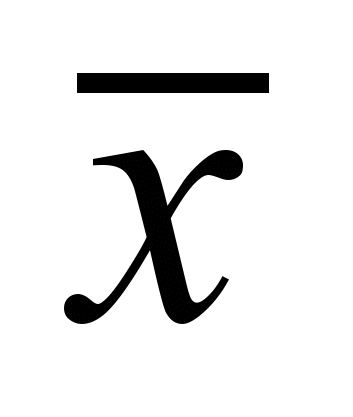 - это вектор переменных, участвующих в решении, а
- это вектор переменных, участвующих в решении, а 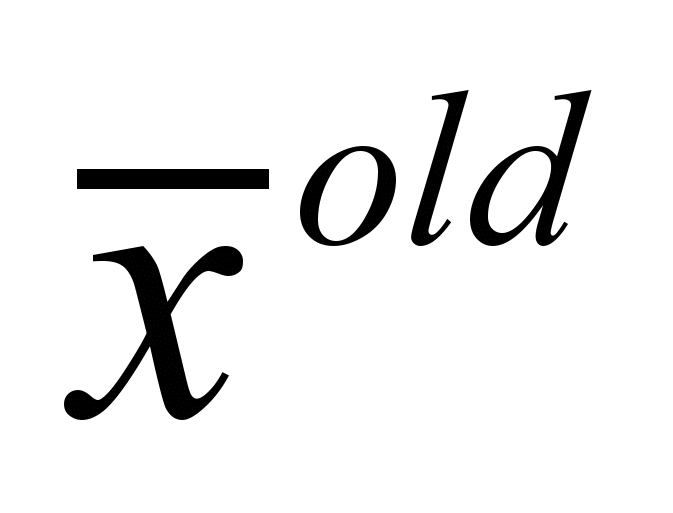 - это вектор констант их старых значений. Функция минимизирует расстояние между новым и старым значением координаты объекта топологии. Операция взятия модуля вносит нелинейность в задачу минимизации, поэтому стандартным симплекс-методом данную задачу не решить. Heng в [10] предложил способ, как линеаризовать данную функцию.
- это вектор констант их старых значений. Функция минимизирует расстояние между новым и старым значением координаты объекта топологии. Операция взятия модуля вносит нелинейность в задачу минимизации, поэтому стандартным симплекс-методом данную задачу не решить. Heng в [10] предложил способ, как линеаризовать данную функцию.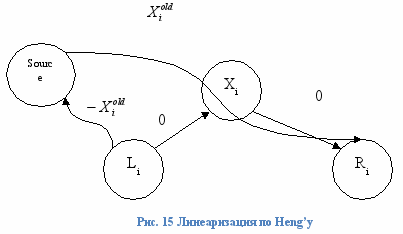
В граф ограничений (рис 15) для каждого
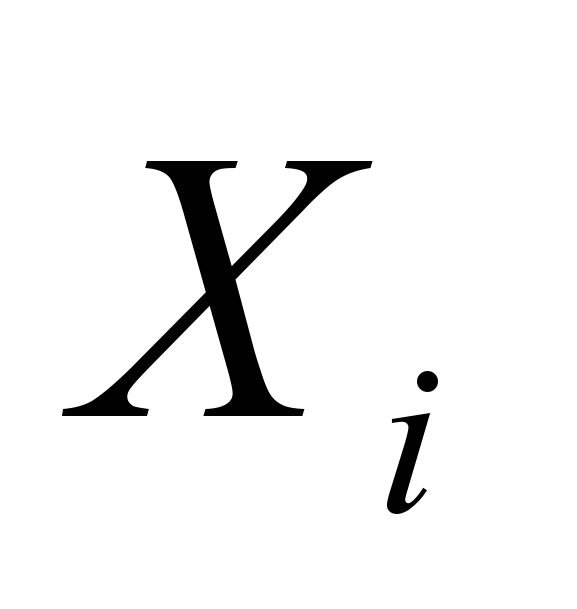 добавляются две переменные
добавляются две переменные 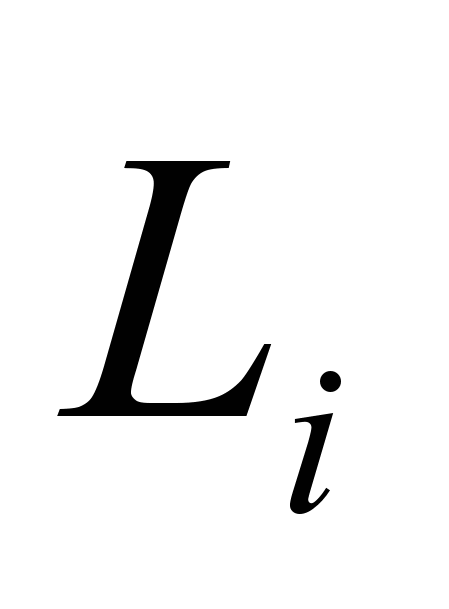 и
и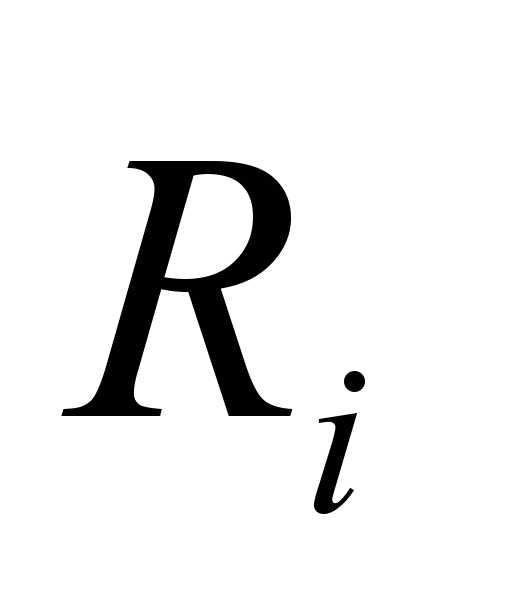 с дополнительными неравенствами, описывающимися следующими ограничениями:
с дополнительными неравенствами, описывающимися следующими ограничениями: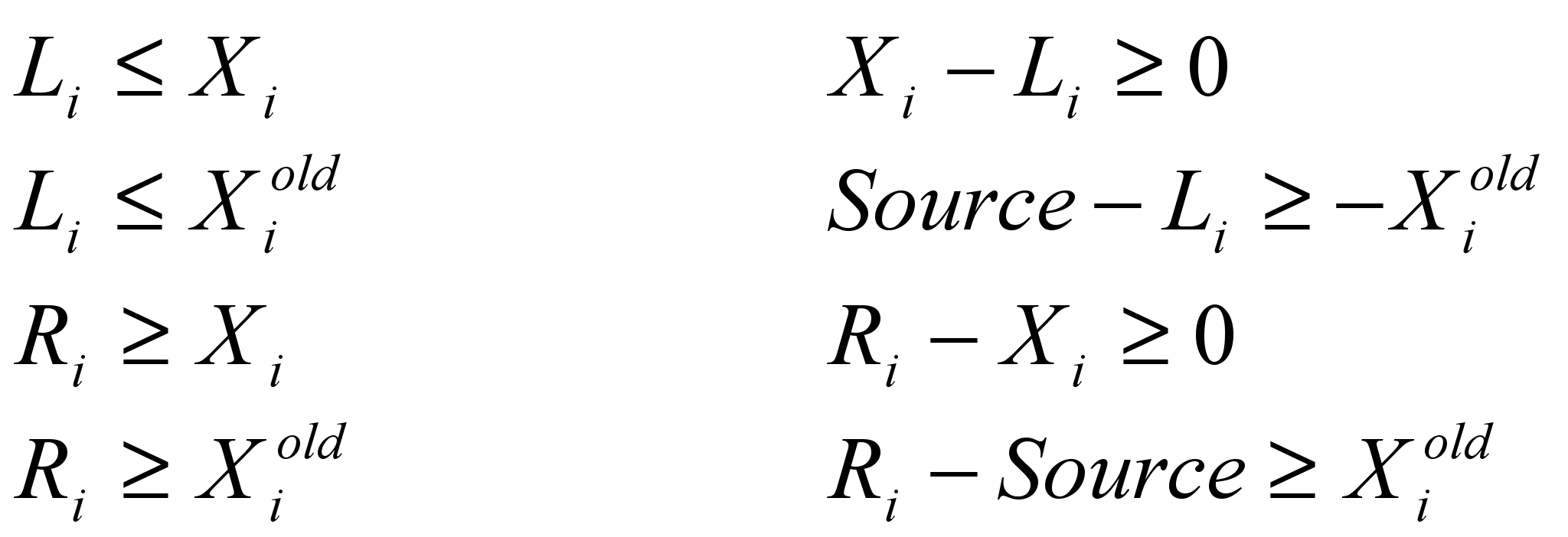 (7)
(7)Функцию минимизации (6) можно представить следующим образом, после введения дополнительных ограничений (7) в граф:
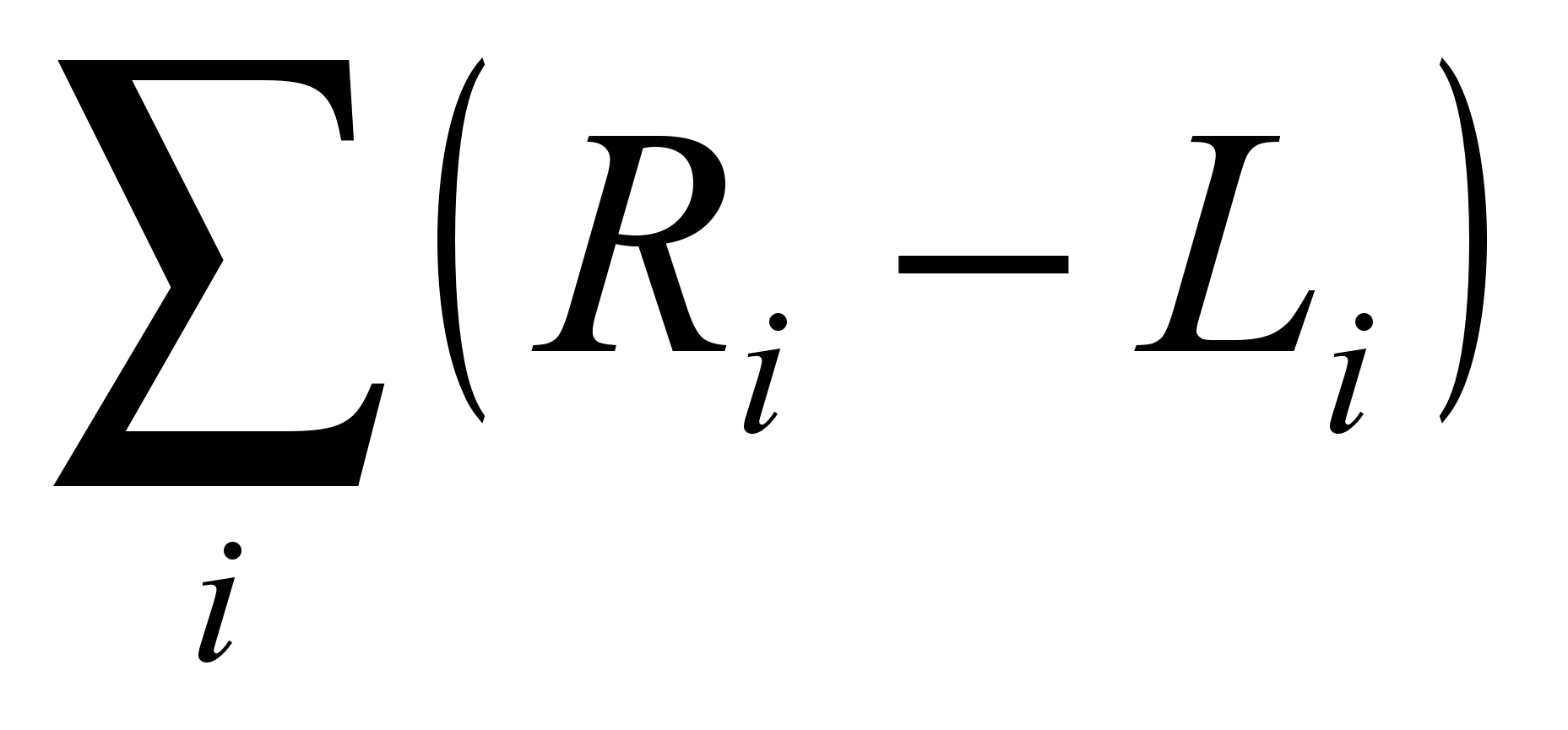 (8)
(8)Недостаток данной функции описан в статье [3] и может быть продемонстрирован на примере:
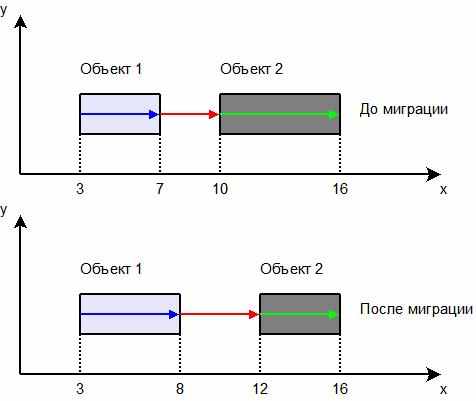
Рис. 14 Миграция с использованием функции (6)
На рис. 16 изображены два объекта топологии в разных слоях в разных технологических процессах до и после миграции соответственно. Топологическая миграция проводилась с учетом 1-D сжатия в X направлении. Для понимания, как ведет себя функция (6) , сделаем еще ряд замечаний, касающихся технологических правил. В исходной технологии правило минимальной ширины для Объекта 1 равнялось 4 условным единицам длинны (у.е.д.) (это значит, что левое ребро Объекта 1 не может находиться ближе к правому, чем на 4 у.е.д.)-темная стрелка, правило минимального интервала между Объектами 1 и 2 равняется 3 у.е.д.- чуть светлее стрелка и правило минимальной ширины для Объекта 2 равнялось 4 - светлая стрелка. В исходной топологии Объект 2 имеет ширину больше, чем 4 у.е.д., поэтому хотелось бы перенести, по возможности, эту ширину в новый технологический процесс. В новом технологическом процессе, правило ширины для Объекта 1 равняется 5 у.е.д., правило минимального интервала между объектами увеличилось до 4, а вот правило минимальной ширины для Объекта 2 осталось равным 4, как и в исходном тех. процессе. Теперь необходимо рассмотреть все разности, старых и новых значений координат ребер объектов 1 и 2. Функция (6) минимизирует разность, поэтому в конечной топологии правое ребро Объекта 2 займет минимально возможное положение, при котором не нарушается правило ширины и функция (6) будет находиться в минимуме.
Также в статье [3] Jianwen Zhu, Frang Fang и Qianying Tang предлагают свою функцию для решения этой проблемы. В статье она фигурирует под названием GC (Geometric closeness):
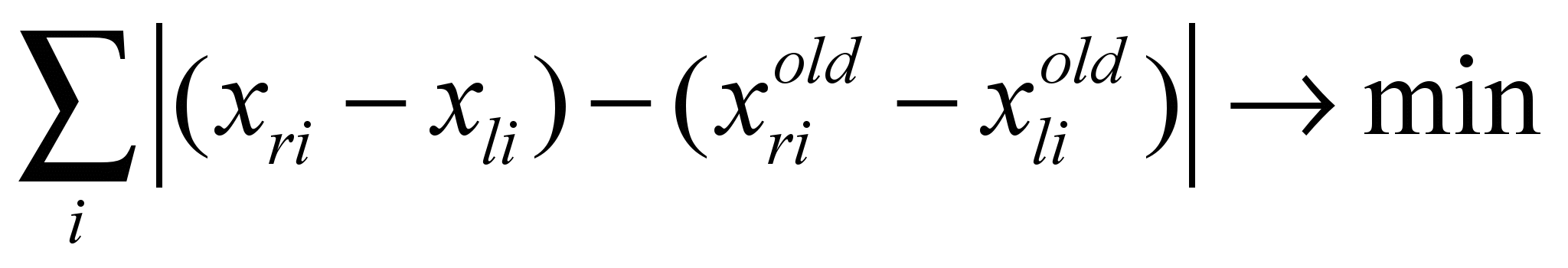 , (9)
, (9)здесь
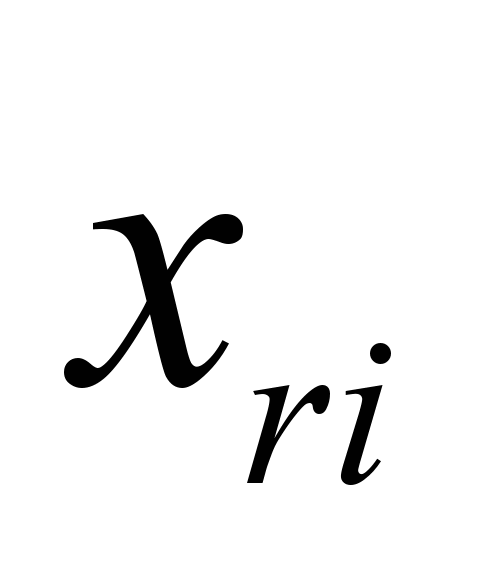 и
и 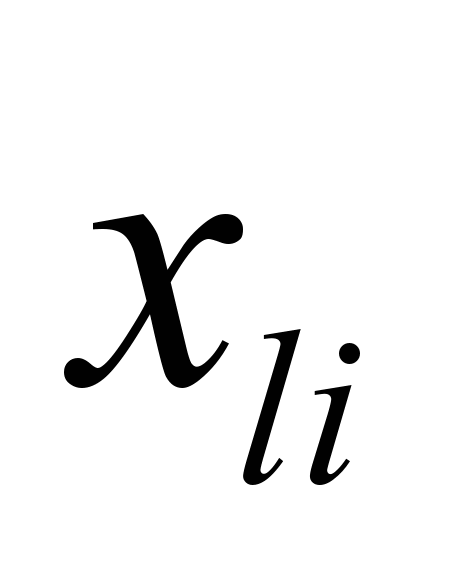 - это
- это 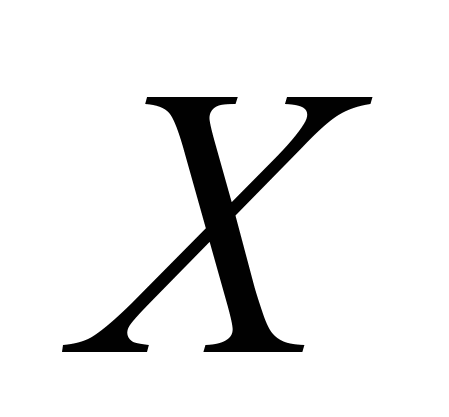 - координаты правого и левого ребра каждой пары ребер i-ого объекта топологии.
- координаты правого и левого ребра каждой пары ребер i-ого объекта топологии.  и
и  - это константы
- это константы 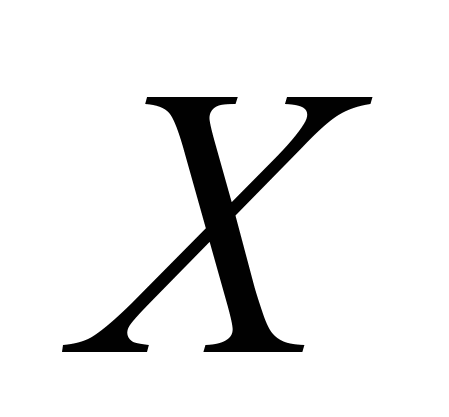 - координат правого и левого ребер соответственно в исходной топологии. Функция (9) вместо минимизации изменения абсолютных значений координат ребер, минимизируется изменение всех фигур топологии.
- координат правого и левого ребер соответственно в исходной топологии. Функция (9) вместо минимизации изменения абсолютных значений координат ребер, минимизируется изменение всех фигур топологии. Так как эта функция содержит операцию модуля, то ее тоже нельзя решить привычными симплекс-методом. Необходимо линеаризовать функцию, избавившись от модуля. Чтобы это проделать воспользуемся материалом статьи [10]. Метод, линеаризует функцию, содержащую модуль, но при этом к набору неравенств добавляется дополнительные неравенства. Для данной функции дополнительные неравенства выглядят так:
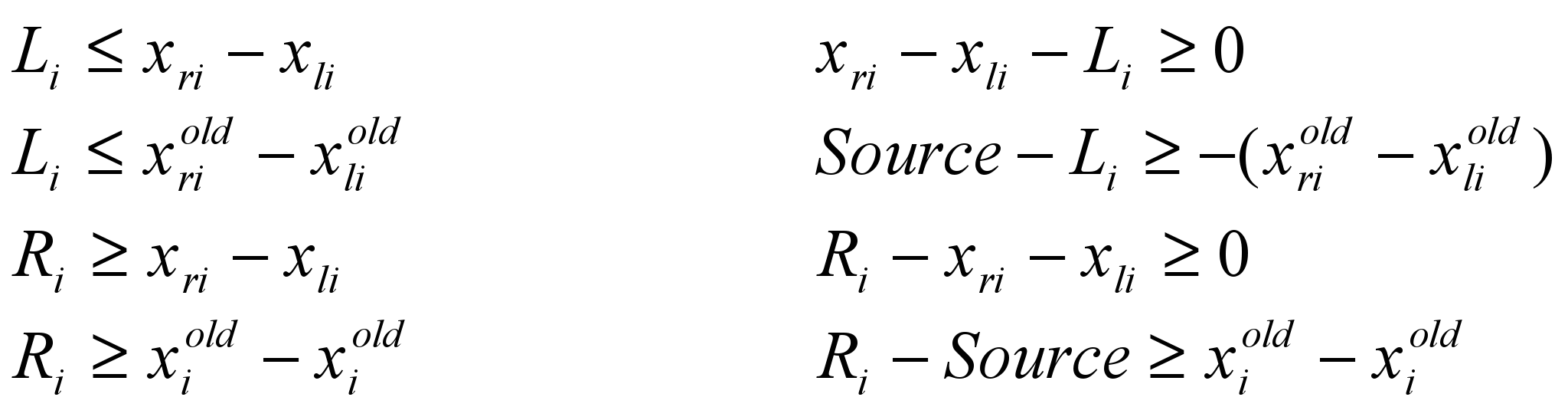 (10)
(10)В нашем случае на каждую пару ребер добавляются две дополнительные переменные
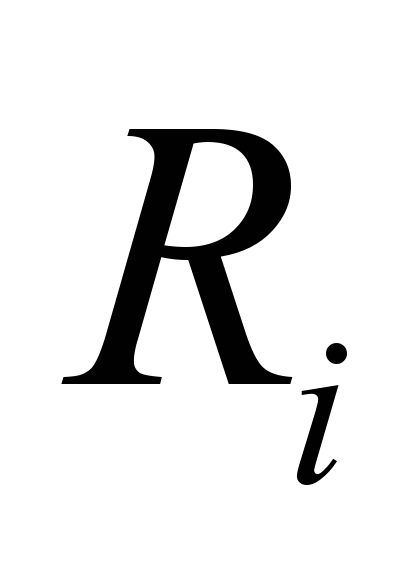 и
и 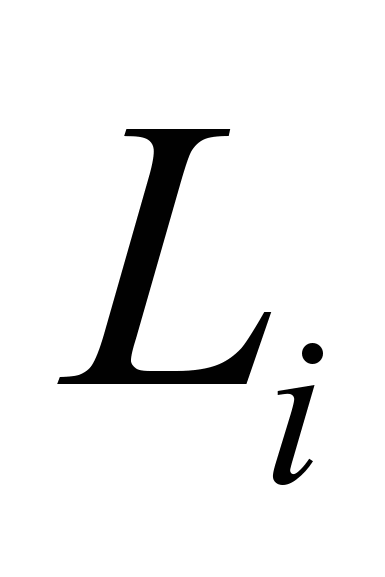 , а целевая функция замениться на
, а целевая функция замениться на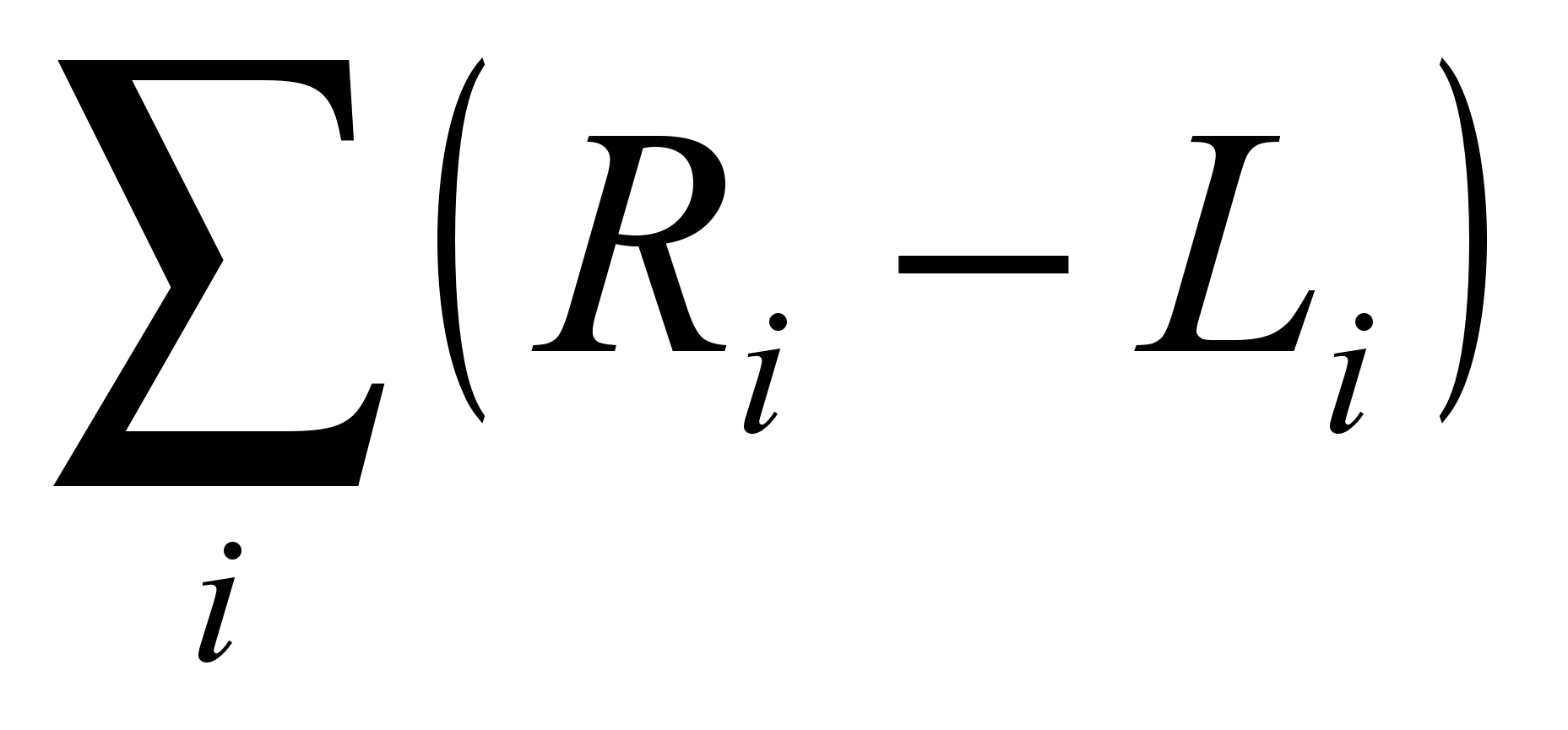 .
.Функция справляется с ситуацией описанной, выше в качестве примера. Поэтому решение для нее будет выглядеть следующим образом:
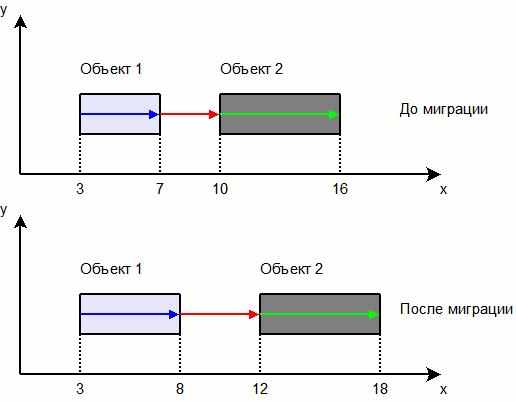
Рис. 15 Миграция с использованием функции (9)
Недостаток данной функции – содержание трех переменных в неравенствах, что означает, невозможность применения модели ортогонального взвешенного графа. Следовательно, если возникнет необходимость мигрировать в сеточную технологию с использованием дополнительных ограничений вида (5), то у нас не будет возможности воспользоваться симплекс-методом.
