Задача минимизации длин проводников 21
| Вид материала | Задача |
- С. В. Шешенин 1/2 года Классические краевые задачи линейной теории упругости в перемещениях., 13.12kb.
- Методы улучшения сходимости алгоритма минимизации функционала, ассоциированного с задачей, 103.65kb.
- О минимизации признакового пространства в задачах распознавания Ветров Д. П., Рязанов, 59.25kb.
- К. П. Ивкин московский инженерно-физический институт (государственный университет), 26.94kb.
- Автоматизированное проектирование схем размещения объектов предприятий из условия минимизации, 124.49kb.
- Проводников в виде участков металлизированного покрытия, размещенных на диэлектрическом, 34.38kb.
- Единый социальный налог: анализ типичных схем минимизации налога, применяемых организациями, 193.29kb.
- Взависимости от числа нанесенных печатных проводников на платы, они разделяются на:, 20.37kb.
- Программа курса лекций «Математические методы и модели исследования операций», 27.98kb.
- Т. М. Боровська кандидат технічних наук, доцент І. С. Колесник, 118.17kb.
1.8Выводы
В данном обзоре были рассмотрены несколько алгоритмов сжатия. Более подробно проведен обзор Графово-теоритического алгоритма сжатия топологии, как одного из самых эффективных на сегодняшний день.
Представлен известный метод решения задач оптимизации основанный на графовом подходе.
Как пример, описана целевая функция минимизации длин проводов. Также рассмотрены две целевые функции минимизирующие изменения, используемые при миграции. Обе функции имеют недостатки. Первая не удовлетворяет по качеству минимизации, а вторая не может быть решена с использованием графового метода, т.к. содержит неравенства с тремя переменными. Поэтому необходимо разработать целевую функцию, которая должна удовлетворять условиям:
- Быть линейной
- Неравенства в задаче должны содержать не больше двух переменных.
Используя целевую функцию и описанные выше алгоритмы сжатия, необходимо разработать подход для миграции топологии с сохранением конфигурации.
Глава 2.Подход для миграции топологии с сохранением конфигурации
2.1Целевая функция
Анализируя графовый метод решения, была рассмотрена следующая ситуация. Если для гипотетической пары вершин Xi и Xj, между которыми необходимо минимизировать изменения расстояния при миграции, необходимо добавить пару вершин li и rj и дополнительные неравенства вида:
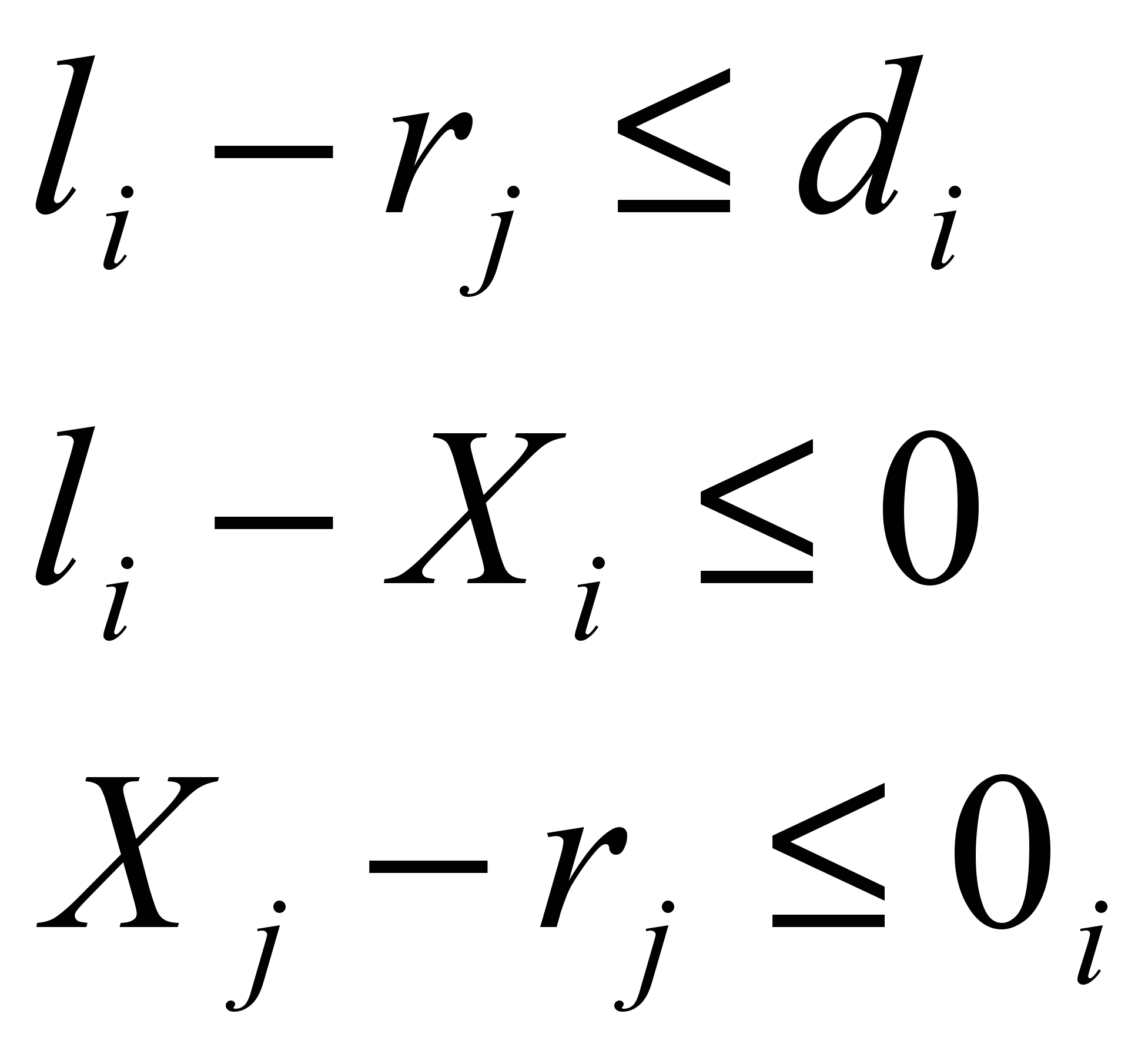(11)И попытаться минимизировать функцию вида:
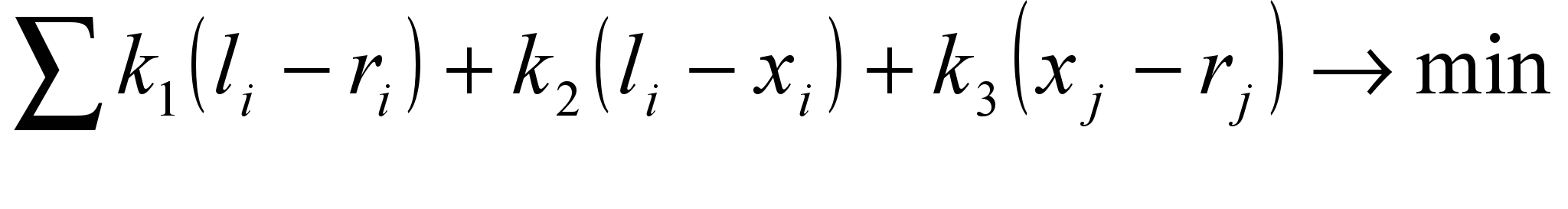то можно получить неплохой результат. Функцию можно упростить до вида:
, (12)если рассмотреть ее модель в графе, то она будет выглядеть так:
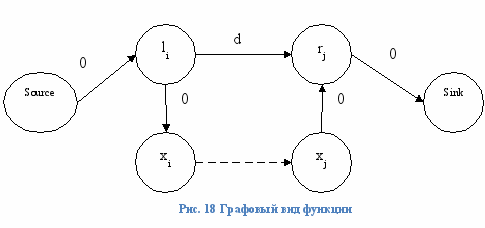
Коэффициенты у вершин li и rj должны быть такими, чтобы графовый метод старался притягивать их друг к другу. Коэффициенты же при Xi и Xj должны быть такие, чтобы графовый метод старался их притягивать к li и rj соответственно. По абсолютному значению коэффициенты при вершинах li и rj должны быть, больше чем при Xi и Xj, для того чтобы достижение величины d было более приоритетно, чем достижение величины в 0 между li и Xi или rj и Xj. Вся картина должна выглядеть следующим образом (Рис. 19). Стрелками показаны ожидаемые движения вершин графа с целью уменьшить значение целевой функции, при наличии свободного интервала.
2.2Уменьшение размерности задачи
Выше описана функция, которая позволяет минимизировать изменения в процессе технологической миграции, где d – это расстояние между двумя топологическими объектами в исходной топологии. Основная проблема данной функции - это размерность. Уменьшение размерности всей задачи состоит из двух этапов:
- Уменьшить общее число расстояний для сохранения конфигурации всей топологии
- Уменьшить размерность самого графа
Первый этап. Стоит отметить, что для того чтобы минимизировать изменения во всей топологии не нужно строить на каждую пару ребер объектов топологии конструкцию в граф ограничений, описанную выше. Топология СЯ достаточно плотная, поэтому необходимо следить только за сохранением конфигурации самих топологических объектов. Предложено, для миграции с сохранением конфигурации минимизировать изменения следующих расстояний:
- ширины всех объектов топологии
- два из трех видов длин ребер топологических объектов
На Рис. 20 указаны эти расстояния для одного объекта топологии.
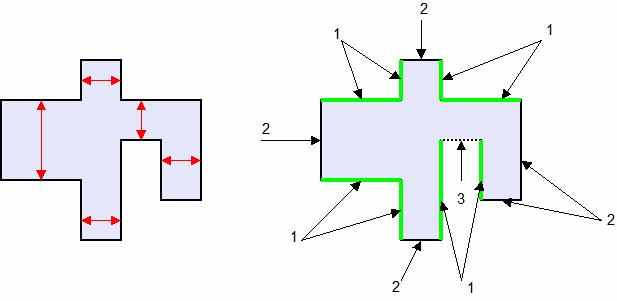
Рис. 16 Расстояния, которые необходимо минимизировать
Для того, чтобы найти все ширины объекта топологии мы используем диаграммы Вороного [11]. На рисунке 21 на левом контуре указаны все эти ширины.
Все длины ребер делятся на три типа: повороты, пики и выемки. Ребра-повороты – это ребра, которые имеют один внешний и один внутренний углы; ребра - пики – имеют два внешних угла; ребра-выемки - имеют два внутренних угла. (На рис 21 обозначен каждый тип цифрами 1, 2 и 3 соответственно) Достаточно минимизировать изменения длин только двух из трех типов ребер: поворотов и выемок.
Второй этап. Уменьшение размерности графа. Рассмотрим пример. На Рис. 21 представлен фрагмент топологии, содержащий два контактных окна и контур, внутри которого они находятся. Необходимо при миграции сохранить расстояния, отмеченные черными стрелками:
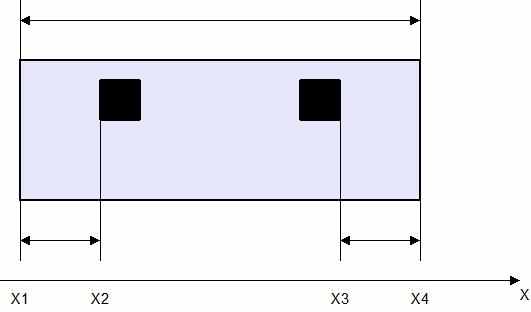
Рис. 17 Фрагмент топологии
Рассмотрим граф, который соответствует данной топологической ситуации (Ребра, соответствующие неравенствам между l вершинами и Source вершиной, а также между r вершинами и Sink, не отмечены, дабы не загромождать рисунок):
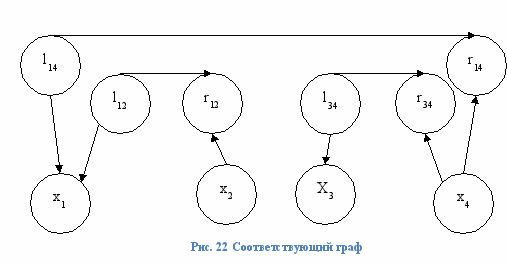
Для каждой пары переменных, между которыми необходимо, cохранить заданное расстояние, необходимо добавить еще пару переменных. Поэтому в худшем случае размерность задачи увеличивается до
, где N2 – это все пары вершин в графе между, которыми необходимо минимизировать изменения. Предлагается, все вершины l при каждой вершине X объединить в одну вершину L, а все r - в R. Где вес для вершины L вычисляется, как сумма весов всех l вершин, входящих в L. Вес R вершин вычисляется как сумма всех весов r вершин, входящих R. Рассмотрим, как это будет выглядеть на нашем графе:
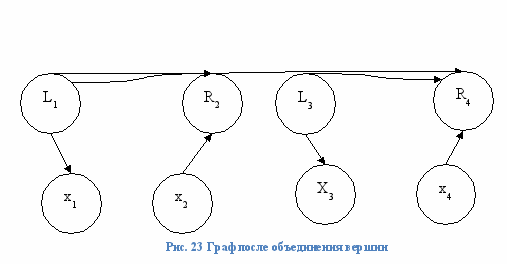
Размерность в этом случае уменьшается до
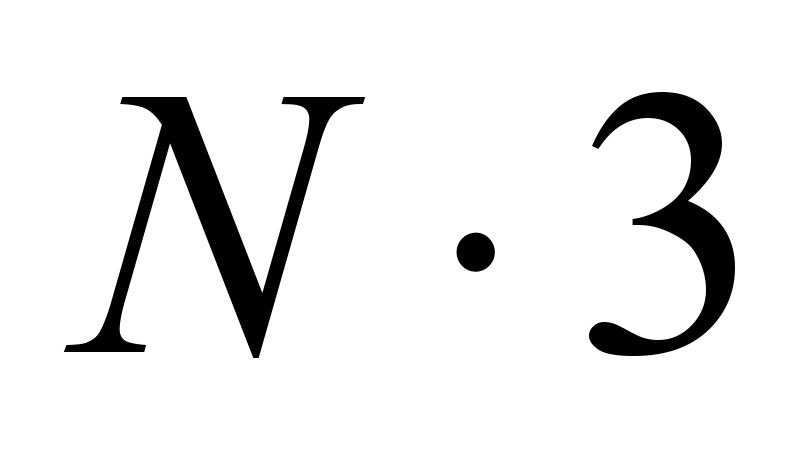, где N - это количество всех X вершин в графе.