Задача минимизации длин проводников 21

Вид материала

Задача

Содержание 1.4Оптимизация топологии. 1.5Графовый метод решения задач оптимизации Рис. 11 Определение групп вершин графа по ребру между вершинами N8 и N9 Рис. 12 Варианты неоптимального и оптимального решения для объекто, не в критическом пути, с учетом сетки. Рис. 13 Выбор координаты технологической сетки для размещения проводника.

Подобный материал:

• С. В. Шешенин 1/2 года  Классические краевые задачи линейной теории упругости в перемещениях., 13.12kb.
• Методы улучшения сходимости алгоритма минимизации функционала, ассоциированного с задачей, 103.65kb.
• О минимизации признакового пространства в задачах распознавания Ветров Д. П., Рязанов, 59.25kb.
• К. П. Ивкин московский инженерно-физический институт (государственный университет), 26.94kb.
• Автоматизированное проектирование схем размещения объектов предприятий из условия минимизации, 124.49kb.
• Проводников в виде участков металлизированного покрытия, размещенных на диэлектрическом, 34.38kb.
• Единый социальный налог: анализ типичных схем минимизации налога, применяемых организациями, 193.29kb.
• Взависимости от числа нанесенных печатных проводников на платы, они разделяются на:, 20.37kb.
• Программа курса лекций «Математические методы и модели исследования операций», 27.98kb.
• Т. М. Боровська кандидат технічних наук, доцент І. С. Колесник, 118.17kb.

1.4Оптимизация топологии.

Все объекты топологии, которые не принадлежат критическому пути, имеют некоторый диапазон координат, в пределах которого могут перемещаться, не увеличивая размер топологии и не нарушив при этом ни одного ограничения. Данный интервал называется свободным или Slack. Положение таких вершин может выбираться исходя из других критериев, таких как минимизация длины проводов, повышение выхода годных и т.д.

Математически данный этап называется оптимизацией и представляет собой решение системы неравенств вида (1) с учетом некоторой целевой функции. Известно, что решая набор неравенств можно получить некоторую область в n-мерном пространстве, где n – это количество переменных в системе неравенств. Если же задать целевую функцию на данной области решений, то можно получить единственное решение, бесконечно много решений или ни одного решения. Система неравенств с заданной целевой функцией представляет собой задачу линейного программирования. В общем виде она выглядит так:

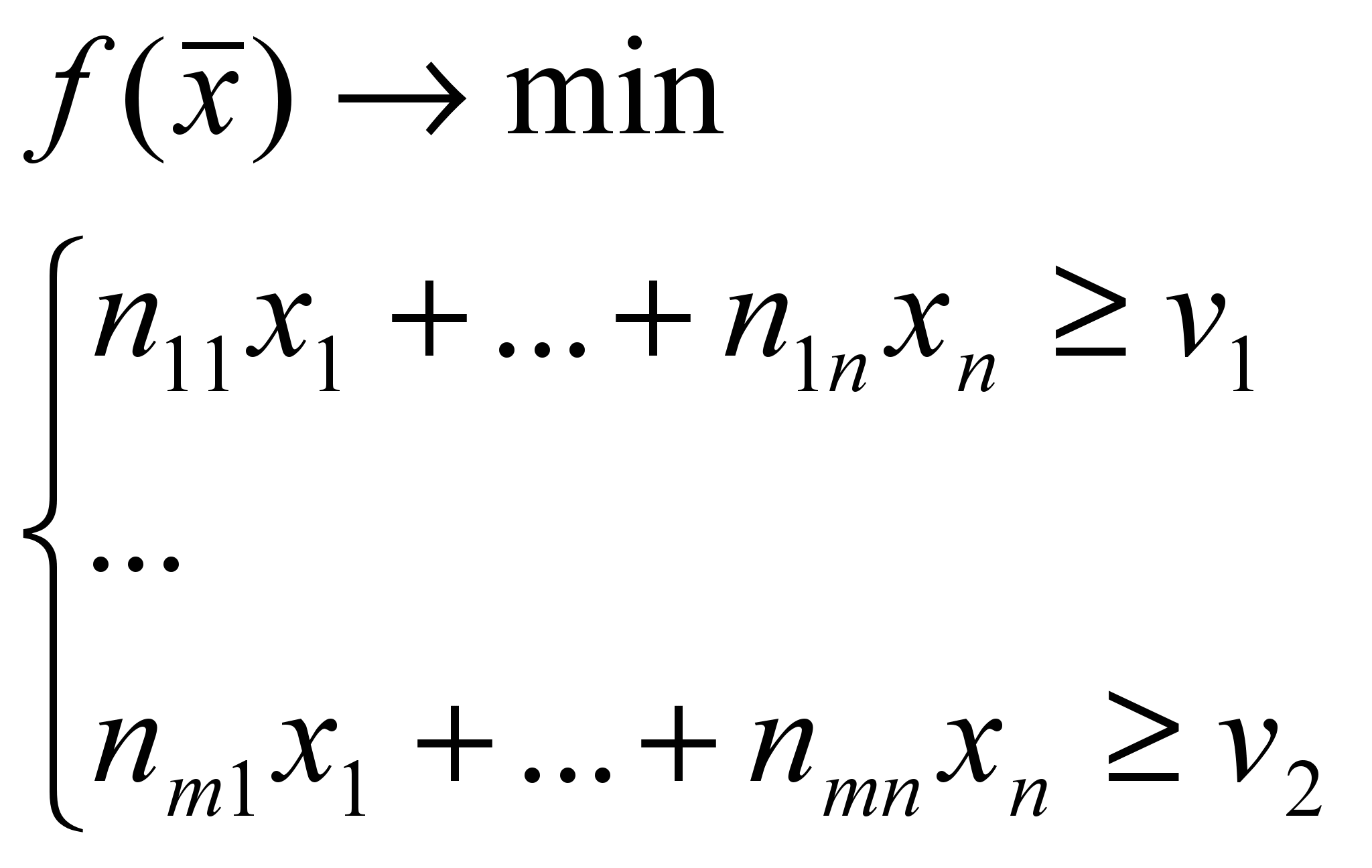(4)

Мы же имеем дело с неравенствами, состоящими из двух переменных вида (1).

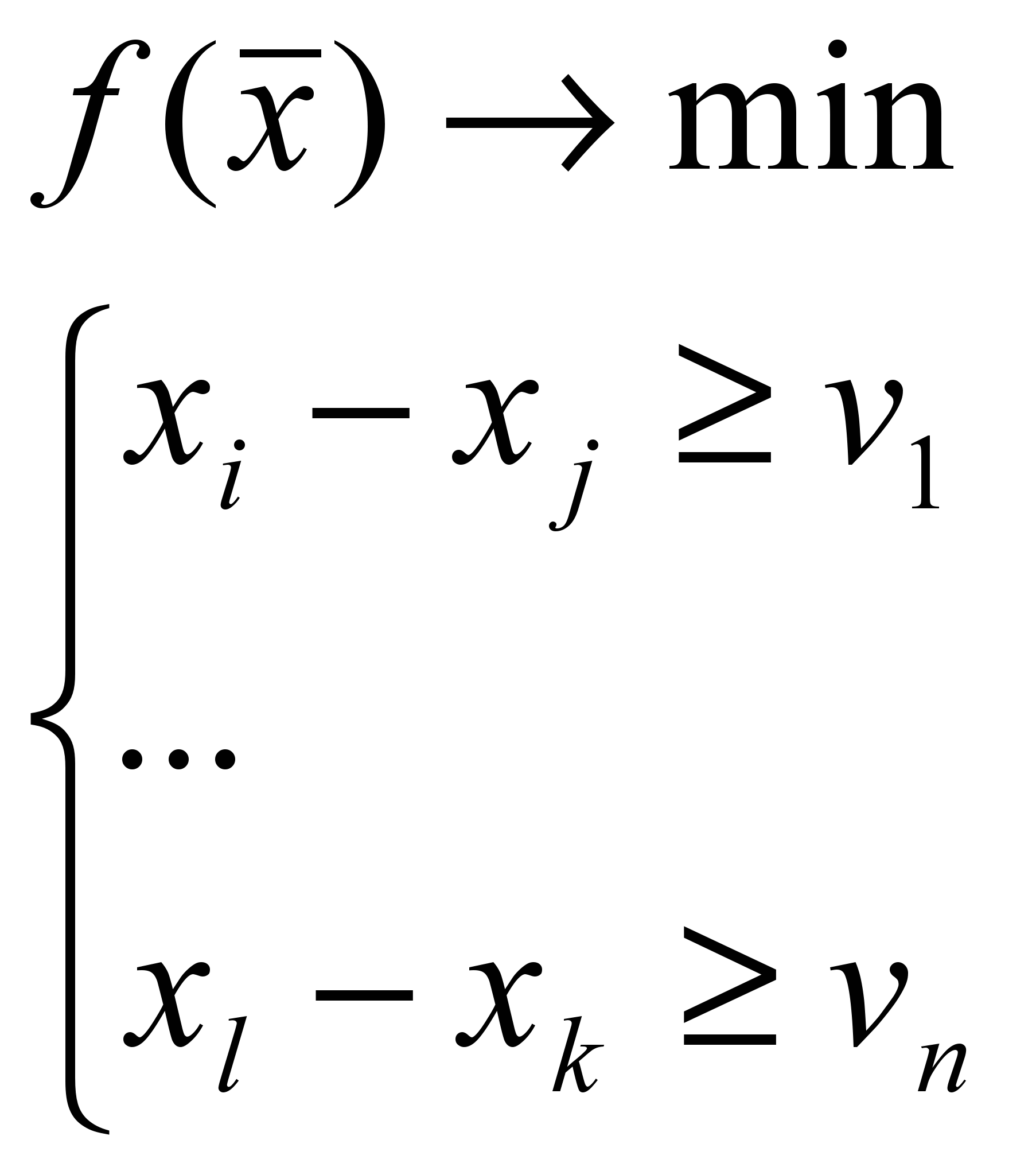(4')

Ограничения в виде неравенств и целевая функция, заданные в виде (4’), могут быть решены как общим – симплекс-методом, так и частным, – графовым. Основные преимущества графового метода перед симплекс-методом следующие:

• В симплекс методе присутствует деление [4], а это значит, что мы имеем дело с дробными величинами, что приводит в итерационном процессе к накоплению ошибок в решении и получению не целочисленного решения. Для того, чтобы получить целочисленное решение, необходимо проводить дополнительные вычисления.
  
• Очень часто требуется внести дополнительные ограничения. В частности, в последних технологических процессах все объекты топологии должны находиться в технологической сетке. Математически это требование может быть представлено:
  

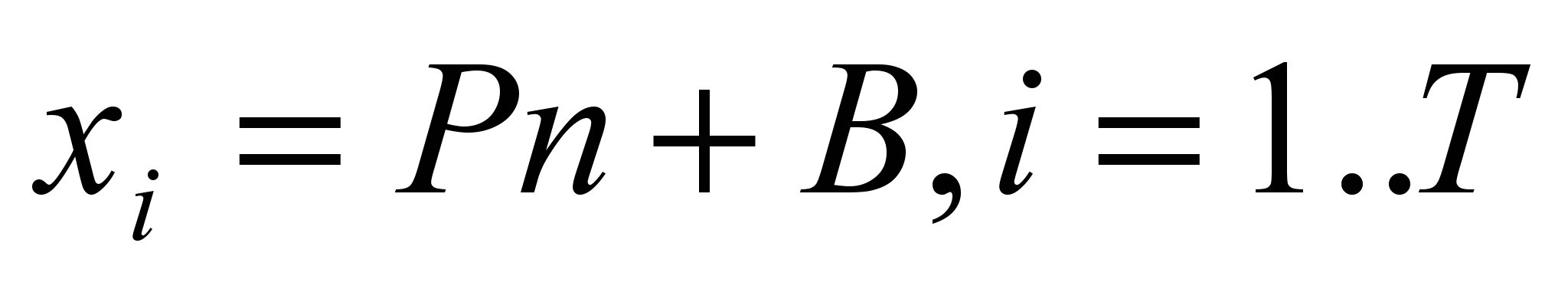, (5)

где X – это координата вершины графа соответствующего объекта, размещаемого в сетке, T – это число объектов, координаты которых должны быть кратны шагу сетки, Р – период, B-смещение технологической сетки относительно начала координат и n – целое число.

• В графовом методе легко находить конфликтные неравенства, т.к. они составляют положительные циклы. Методы, которые реализуют симплекс-метод, не предоставляют такой возможности.
  

Важно подчеркнуть, что задача оптимизации вида (4) или (4') с дополнительными ограничениями вида (5) уже не является линейной, поэтому уже не может быть решена симплекс-методом.

1.5Графовый метод решения задач оптимизации

Поскольку симплекс-метод требует обработки большого объема информации в виде таблиц, был предложен подход, использующий граф ограничений. В этом случае каждой вершине графа приписывается вес, равный сумме коэффициентов при соответствующей переменной в целевой функции (4'). Вычисленный таким образом вес вершины показывает направление перемещения объекта топологии, связанного с этой вершиной. Если вес вершины больше нуля, это направление совпадает с направлением сжатия, в случае же веса меньше нуля – это противоположное направление. Как известно, симплекс - метод минимизирует функцию путем перехода от одного допустимого решения к другому, требуя изменения только одной базовой переменной. Это требование приводит к тому, что в графе ограничений в каждый момент времени существует множество подграфов, каждый из которых является деревом. В вершине этих деревьев находятся неподвижные вершины, то есть вершины, координаты которых нельзя изменять. Каждое ребро, принадлежащее такому подграфу, имеет минимально возможную длину и называется критическим. Такие ребра соответствуют базовым переменным симплекс-метода. Минимизация может начинаться только с допустимого решения. Доказано [6], что граф, соответствующий топологии, полученный в результате сжатия, удовлетворяет такому требованию, поскольку на нем всегда можно найти множество соответствующих подграфов, являющихся деревьями.

Поскольку в [6] излагаются только общие идеи, то в [5] Плеханов А.С. указал метод, который позволяет решить задачу минимизации с дополнительными ограничениями, указанными в (5). Проиллюстрируем это на примере. На Рис. 11 показан граф, соответствующий некоторой топологии после сжатия. Все вершины графа имеют минимально возможные координаты и определенный вес. Возьмем ребро между вершинами N8(FromNode) и N9(ToNode). Это ребро принадлежит подграфу, в который входит вершина Source, NN3,4,5,7,8,9,10 и Sink, а принадлежащие ему ребра показаны сплошными стрелками. Делим этот подграф на два подграфа таким образом, чтобы вершина N8 входила в один, а N9 – в другой. Первый подграф состоит из вершин Source, NN3,4,7 и 8, а второй – из вершин NN9,5,6,10 и Sink. Теперь вершина Source, являющаяся вершиной исходного подграфа, содержится в первом из полученых подграфов. Следовательно, группу формируем из вершин NN 9,5,6,10 и Sink.



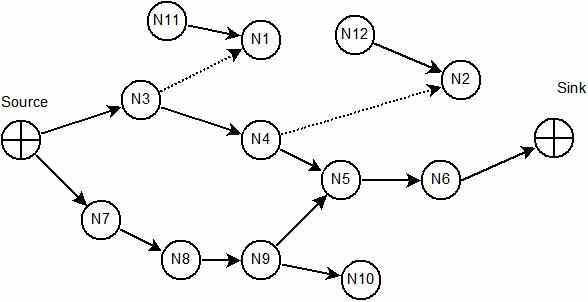
Рис. 11 Определение групп вершин графа по ребру между вершинами N8 и N9

Вычисляем вес полученной группы, как сумму весов всех входящих в нее узлов. Аналогично весу отдельного узла, вес группы показывает направление ее перемещения для уменьшения суммарной задержки.

Выполняется данное перемещение групп до тех пор, пока можно осуществить хотя бы одно изменение координат вершин графа, приводящее к уменьшению целевой функции.

Следует отметить важное обстоятельство: в результате этих действий, несмотря на изменение состава и конфигурации подграфов, общая структура графа в виде множества деревьев остается неизменной.

При учете дополнительных ограничений вида (5) задача перестает быть линейной. Дополнительные ограничения приводят к тому, что координата объекта топологии, может иметь только дискретные значения в свободном интервале. В соответствии с этим координаты вершин, входящих в группу, содержащую данную вершину, также будут принимать только дискретные значения. Это приводит к тому, что решение, полученное приведенным выше алгоритмом, будет не оптимальным.

На Рис. 12a объекты, которые находились не в критическом пути, получили неоптимальное решение согласно алгоритму, описанному выше. Алгоритм, описанный в [5], позволяет получать решения в сетке Рис. 12b.



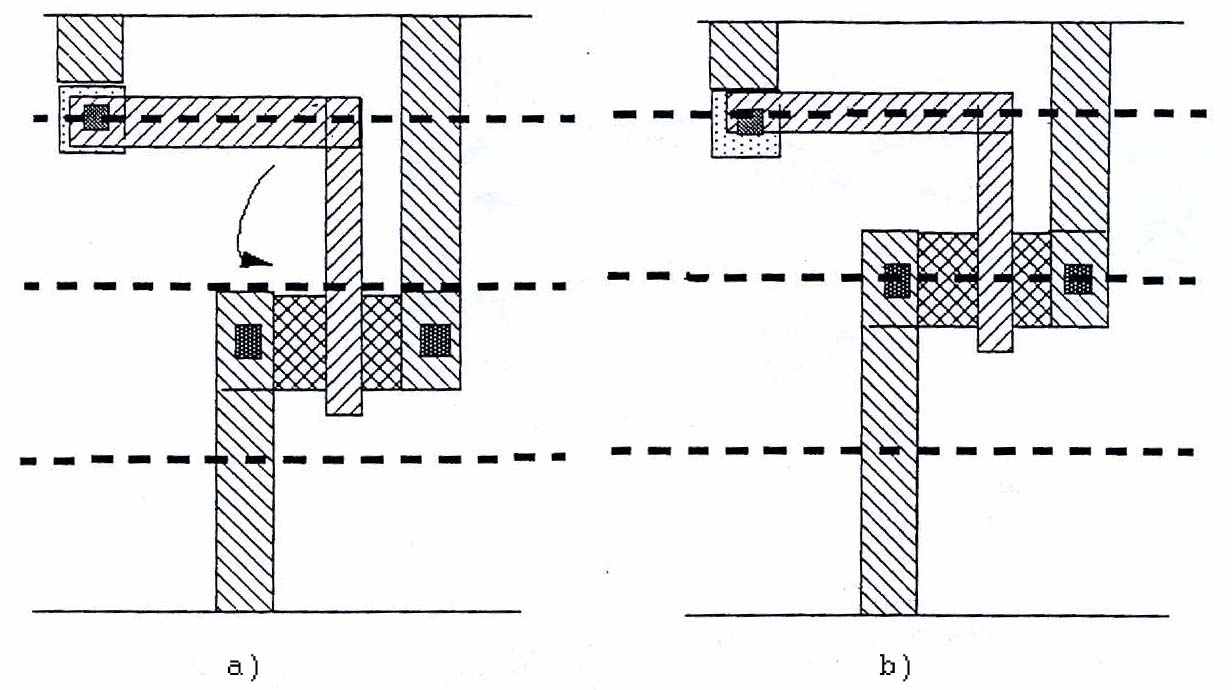
Рис. 12 Варианты неоптимального и оптимального решения для объекто, не в критическом пути, с учетом сетки.

Метод решения состоит из двух этапов. На первом этапе ограничения, накладываемые сеткой, не учитываются, и решение получают изложенным выше способом. На втором этапе заданные топологические объекты размещаются в координатах, кратных технологической сетки. При этом используется решение, полученное на первом этапе. Поскольку решение, полученное на первом этапе, является оптимальным, без учета (5), то любое изменение координат топологических объектов либо ухудшает значение целевой функции, либо оставляет его неизменным.

Для решения любой задачи минимизации, заданной в (4) с учетом (5), необходимо найти такие новые координаты объектов, при которых заданные топологические объекты находились бы в технологической сетке, а ухудшение целевой функции было бы минимальным. Предположим, что имеется один объект (Рис 13), который необходимо разместить в технологической сетке. Для этого необходимо выбрать координату сетки, в которую будет устанавливаться заданный объект топологии. Пусть координатой объекта является X, а ближайшие координаты технологической сетки есть X₀ и X₁ (X₀1>X).



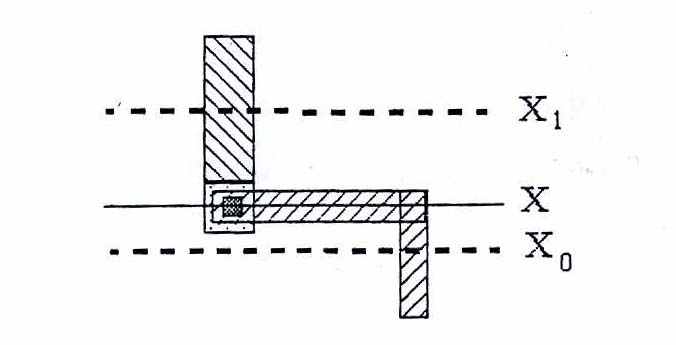
Рис. 13 Выбор координаты технологической сетки для размещения проводника.

Таким образом, задача установки объекта в сетку сводится к задаче оптимального перемещения объекта из одной координаты в другую.