Задача минимизации длин проводников 21
| Вид материала | Задача |
- С. В. Шешенин 1/2 года Классические краевые задачи линейной теории упругости в перемещениях., 13.12kb.
- Методы улучшения сходимости алгоритма минимизации функционала, ассоциированного с задачей, 103.65kb.
- О минимизации признакового пространства в задачах распознавания Ветров Д. П., Рязанов, 59.25kb.
- К. П. Ивкин московский инженерно-физический институт (государственный университет), 26.94kb.
- Автоматизированное проектирование схем размещения объектов предприятий из условия минимизации, 124.49kb.
- Проводников в виде участков металлизированного покрытия, размещенных на диэлектрическом, 34.38kb.
- Единый социальный налог: анализ типичных схем минимизации налога, применяемых организациями, 193.29kb.
- Взависимости от числа нанесенных печатных проводников на платы, они разделяются на:, 20.37kb.
- Программа курса лекций «Математические методы и модели исследования операций», 27.98kb.
- Т. М. Боровська кандидат технічних наук, доцент І. С. Колесник, 118.17kb.
2.5Выводы
Предложено использовать целевую функцию вида (12) с дополнительными ограничениями (11). Функция добавляет ограничения только с двумя переменными, поэтому можно использовать существующий способ решения, основанный на графовом подходе, который также позволяет находить решение в сетке.
Предложены методы по уменьшению размерности задачи с использованием целевой функции (12).
Предложен дополнительный метод по центрированию сток/исток контактов и контактов металлических поликремневых участков цепи.
Глава 3.Программная реализация
3.1Формальное описание работы алгоритма сжатия и миграции
В качестве входной информации требуются формальные описания технологических правил, шаблона (архитектуры) ячейки, и исходная топология. Выходной информацией является топология, удовлетворяющая требованиям технологических правил. Основные потоки данных представлены на Рис.30. Хотя задачи сжатия и миграции топологии несколько отличаются форматами входных/выходных данных и предварительной обработкой топологии, обе используют общий базовый алгоритм, представленный на Рис.31. В основе системы лежит алгоритм 1.5-мерного сжатия топологии [2]. Так как при 1,5-мерном сжатии минимизируется размер топологии только в основном направлении, то необходимо последовательно применять данный алгоритм для вертикального и горизонтального направлений. Данная последовательность определяется тем, что топология стандартной ячейки должна иметь фиксированную высоту, поэтому вертикальное сжатие должно выполняться первым. Если при этом не удалось достичь заданной высоты, то дальнейшее сжатие не выполняется. После проведения сжатия топологии по обоим направлениям выполняется оптимизация топологии, по какой либо целевой функции, либо минимизации длин проводника, либо минимизация изменений при миграции.

Рис. 24 Входные и выходные данные системы сжатия и миграции топологии

Рис. 25 Блок-схема процесса сжатия топологии
1.5-мерное сжатие [2] - итеративный процесс, где на каждой итерации выполняется одномерное сжатие. После одномерного сжатия выделяется минимальное подмножество объектов, которые препятствуют уменьшению размера топологии в направлении сжатия. Затем выбранные объекты сдвигаются в сторону. Итерации повторяются пока размер топологии уменьшается или не достигнут целевой размер, т.е. высота стандартной ячейки или ее оценка.
3.2Программная реализация этапа оптимизации топологии
Весть процесс миграции реализован на языке высокого уровня С++. Нами был изменен этап оптимизации, представленный в виде класса Minimizer. Класс оперирует двумя дополнительными классами: Mover и WeightComputer. Класс Mover отвечает за движение вершин согласно графовому алгоритму минимизации описанному в [5]. Класс WeightComputer отвечает за установку весов, согласно целевой функции и файлу параметров, в котором описаны значения приоритетов для каждого стоя. UML диаграмма класса представлена на рисунке:
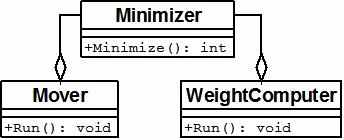
Рис. 26 UML диаграмма класса Minimizer
3.3Обзорный пример
Как было выше сказано, большинство САПР выполняют различные виды задач. Здесь я постараюсь обзорно показать каждый этап работы системы миграции топологии одной из стандартных ячеек. Рассматриваться будет одна итерация сжатия по Y-направлению для переноса топологии на другую архитектуру, с большим количеством треков. При миграции использовались функции минимизации длин проводников и минимизации изменений. Схематично весь процесс можно представить в виде блок схемы (рис 33).
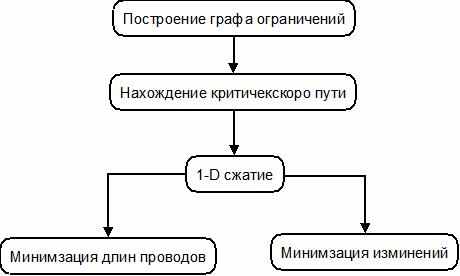
Рис. 27 Блок-схема одной итерации миграции СЯ
Рассмотрим входную топологию, высота ячейки составляет 8 треков:
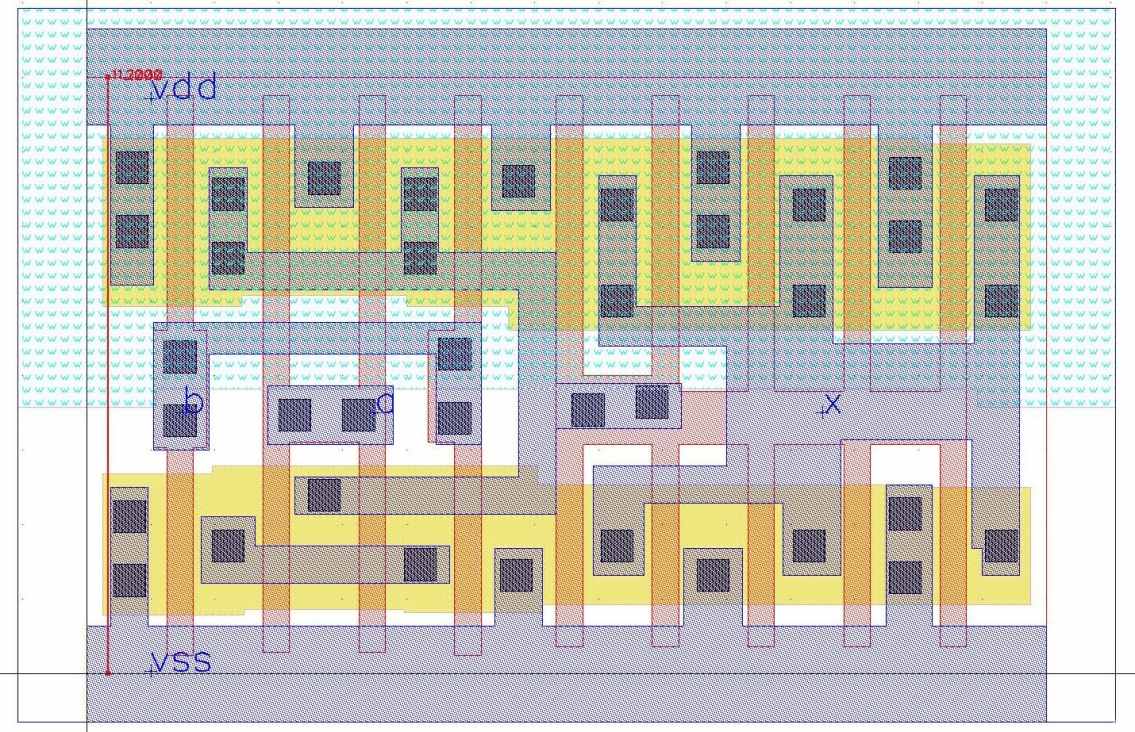
Рис. 28 Входная топология ячейки and2_8
Первое этап – это построение ограничений. Нарушенные ограничений выделены темным цветом, именно они входят в критический путь и заставляют ячейку увеличиться на один трек:
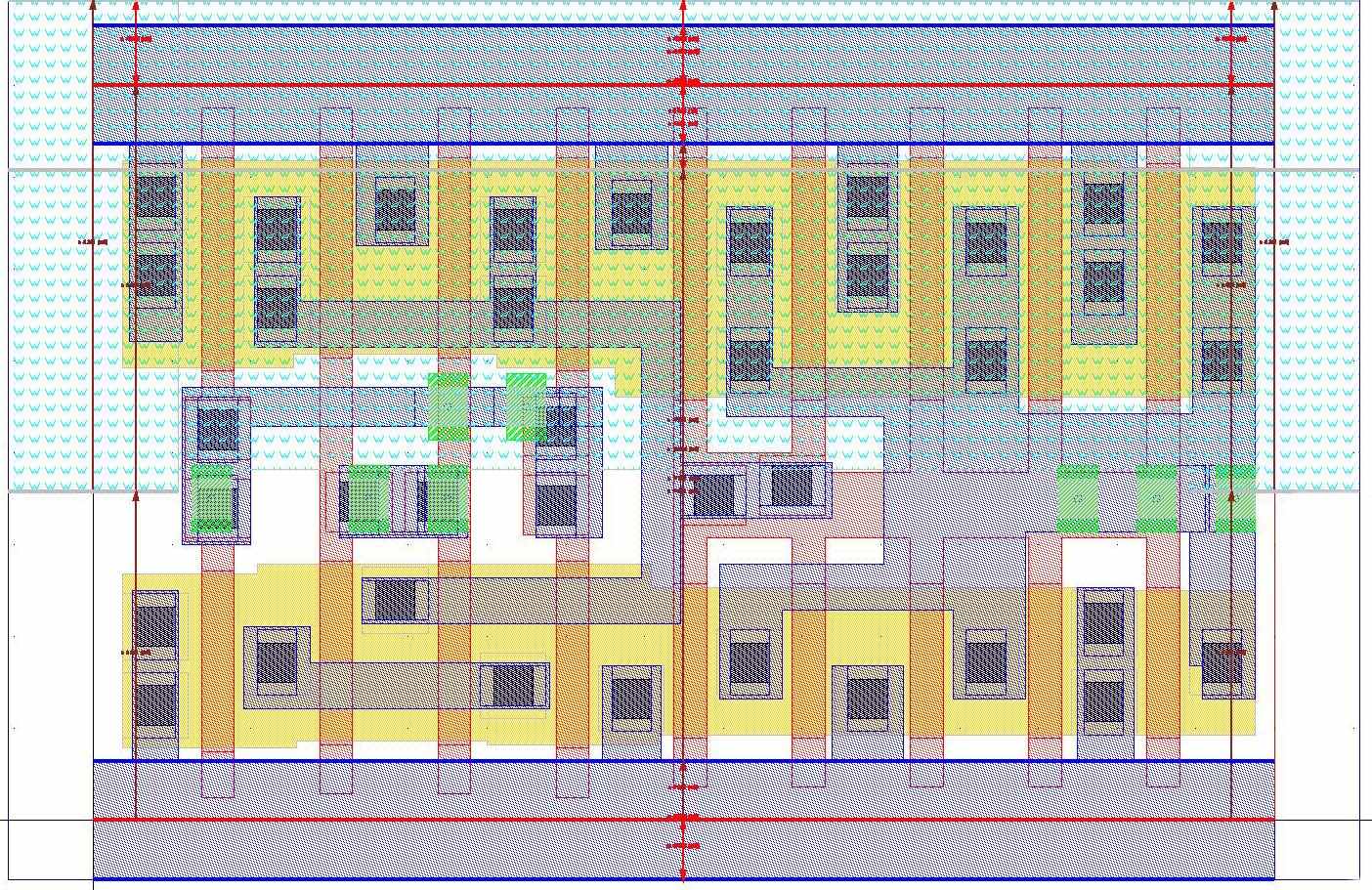
Рис. 29 Построение ограничений, выделение нарушенных ограничений.
Следующий этап – это использование 1D-сжатия в вертикальном направлении. Все объекты топологии встают на минимально возможные координаты, которые позволяют им технологические правила.
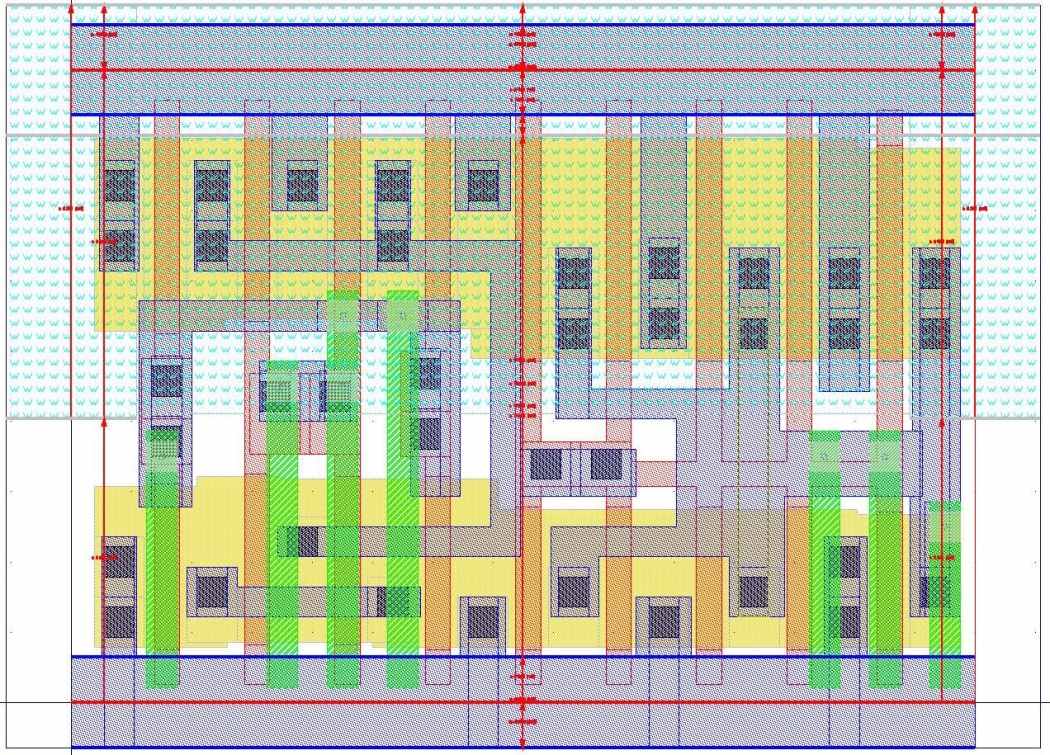
Рис. 30 Установка в минимум всех объектов топологии.
Далее происходит оптимизация топологии. Все объекты, которые имеют свободный интервал, участвуют в работе минимизационной функции. На выходе можно получить топологический шаблон с минимальными длинами проводников:
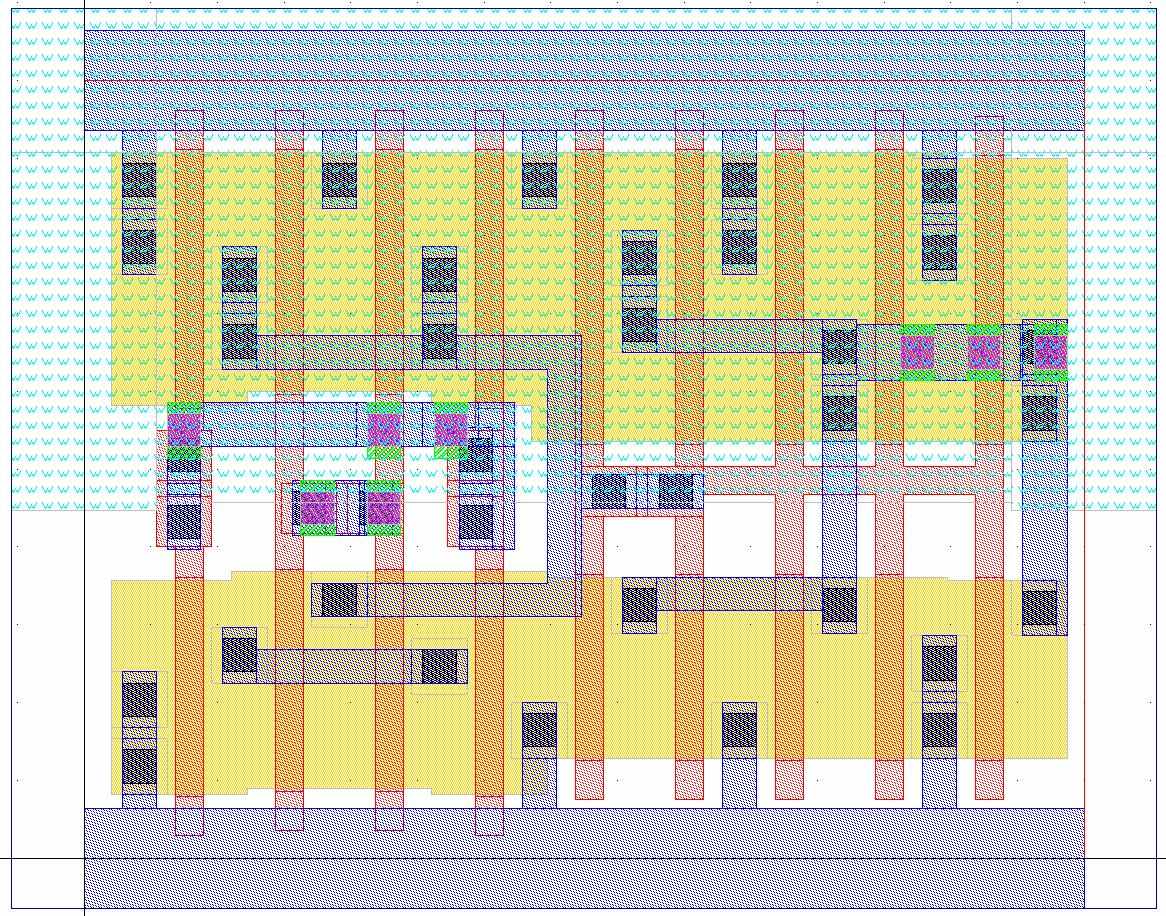
Рис. 31 Минимизация длин проводников.
или минимизация изменений:
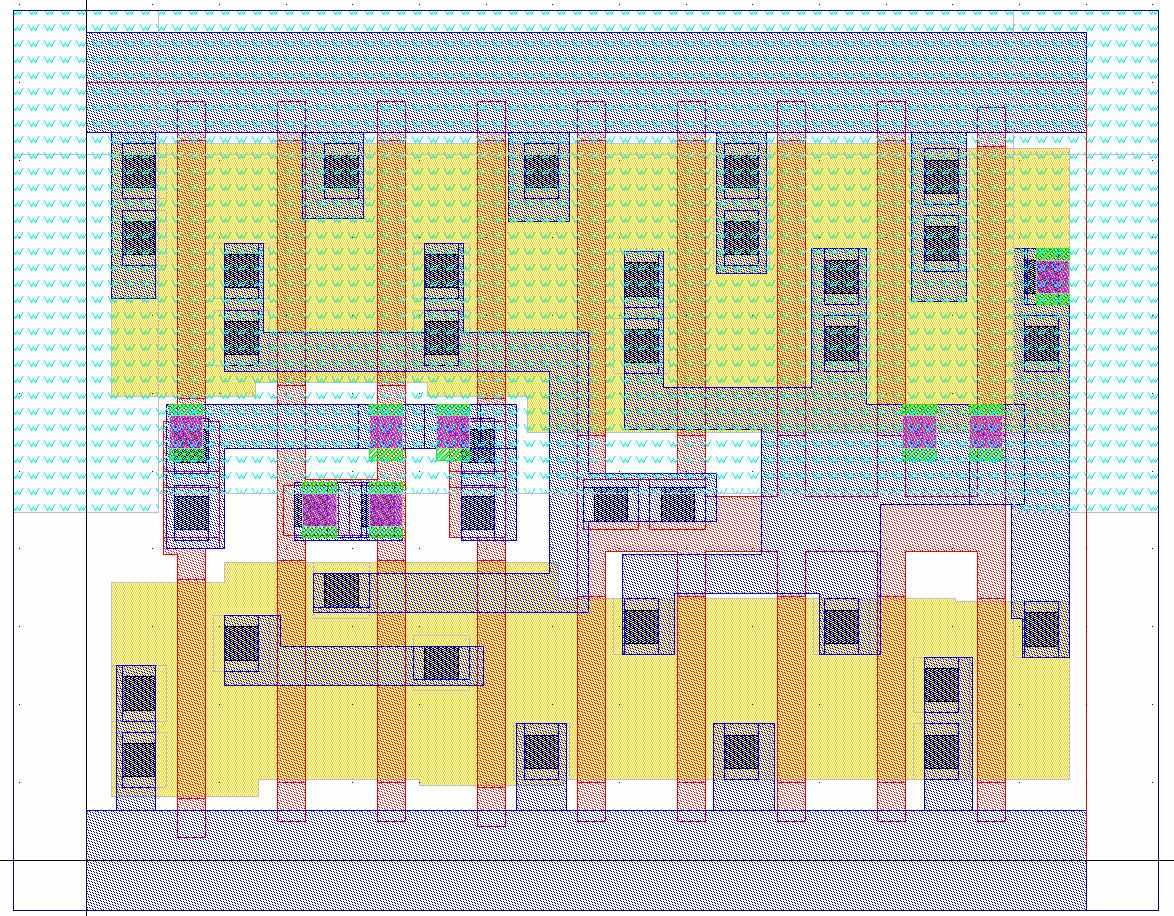
Рис. 32 Минимизация изменений при миграции.
В данной работе рассматривалась программная система автоматического сжатия и миграции топологии стандартных ячеек КМОП СБИС, разработанная в компании Freescale Semiconductor. Система поддерживает технологические процессы с минимальными размерами до 32 нм и используется для миграции топологии библиотек стандартных ячеек.
