Задача минимизации длин проводников 21
| Вид материала | Задача |
- С. В. Шешенин 1/2 года Классические краевые задачи линейной теории упругости в перемещениях., 13.12kb.
- Методы улучшения сходимости алгоритма минимизации функционала, ассоциированного с задачей, 103.65kb.
- О минимизации признакового пространства в задачах распознавания Ветров Д. П., Рязанов, 59.25kb.
- К. П. Ивкин московский инженерно-физический институт (государственный университет), 26.94kb.
- Автоматизированное проектирование схем размещения объектов предприятий из условия минимизации, 124.49kb.
- Проводников в виде участков металлизированного покрытия, размещенных на диэлектрическом, 34.38kb.
- Единый социальный налог: анализ типичных схем минимизации налога, применяемых организациями, 193.29kb.
- Взависимости от числа нанесенных печатных проводников на платы, они разделяются на:, 20.37kb.
- Программа курса лекций «Математические методы и модели исследования операций», 27.98kb.
- Т. М. Боровська кандидат технічних наук, доцент І. С. Колесник, 118.17kb.
2.3Обзор подхода
Наш подход сохранения конфигурации топологии при миграции получает решение приоритетного вида. В нашем случае – это либо минимизация изменений ширин, либо минимизация изменений длин. Решение, которое содержит и минимальное изменение ширин и минимальное изменение длин, в нашем подходе не получить. Поэтому всегда возможны два решения. Рассмотрим эти решения на примере миграции топологии из одной архитектуры в другую. Конечная архитектура имеет большее количество треков, поэтому высота библиотечного элемента и целевой архитектуре больше. Топология входная ячейки имеет вид:
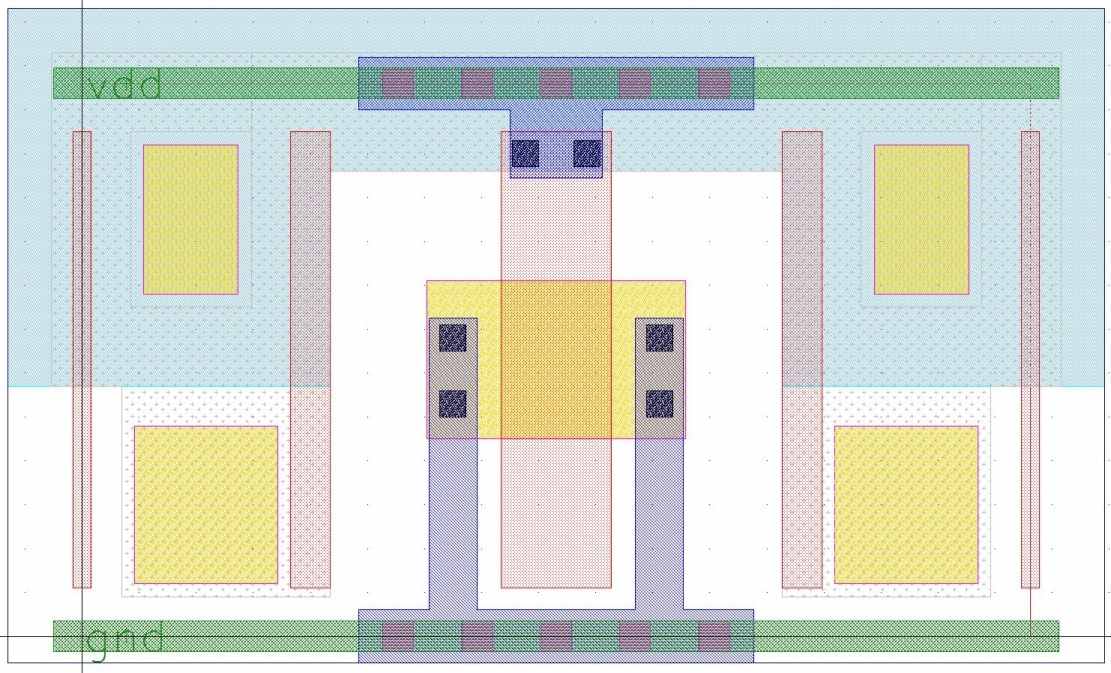
Рис. 18 Топология входной ячейки
Теперь рассмотрим результаты возможных миграций с различными условиями.
Первый случай, это миграция с возможностью минимизаций изменений длин N-кармана. На рисунке 28 черными стрелками указаны ребра N-кармана, минимизация изменений которых была в приоритете. Изменения ширин в данном случае минимизированы в меньшей степени.
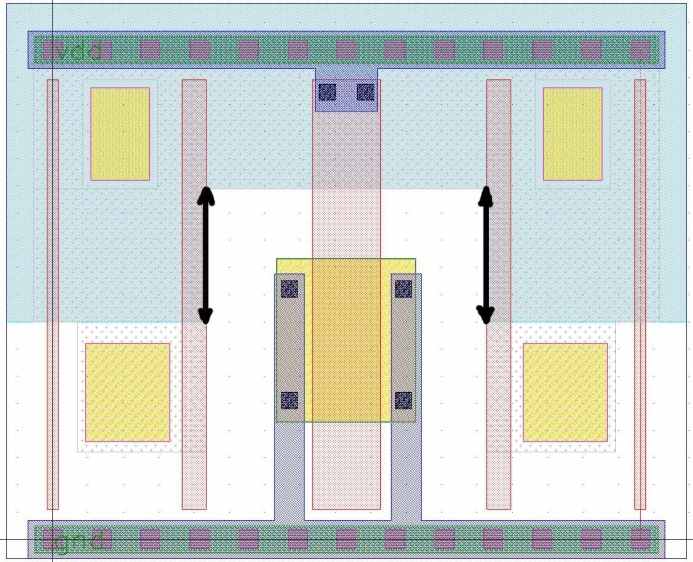
Рис. 19 Миграция с приодитетом длин
Второй случай, это миграция с возможностью минимизаций изменений ширин N-кармана. На рисунке 29 черной стрелкой указана ширина N-кармана, минимизация изменений которой была в приоритете. Изменения длин в данном случае минимизированы в меньшей степени.
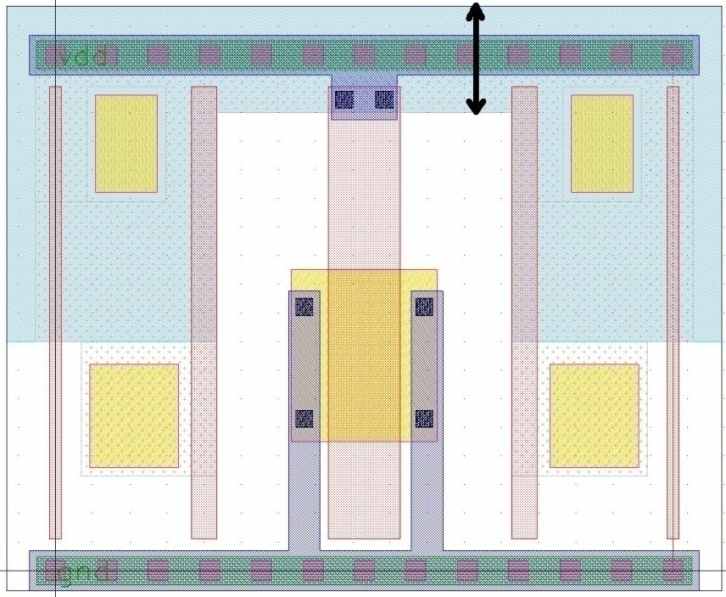
Рис. 20 Миграция с приоритетом ширин
Так как решения получаются в общем случае двух видов, то для того чтобы не потерять данной гибкости была введена система настроек для каждого топологического слоя в системе миграции. К набору параметров слоя были добавлены еще два параметра. Первый из них отвечает за сохранение всех ширин, а второй - за сохранение длины ребер объектов на данном слое. Значения для параметров формально описывают приоритет, в котором будут минимизированы изменения длин и ширин. Значения двух параметров могут быть: выключено, низкий приоритет и высокий приоритет. В выключенном состоянии минимизация изменений не проводится для данного параметра. Разница между значениями высокий и низкий приоритет составляет разницу в коэффициентах для целевой функции.
2.4Возможности целевой функции
Возможности данной целевой функции не ограничены только сохранением конфигурации всей топологии СЯ. Расстояние между переменными L и R можно задать любое и пытаться его сохранить. На этой возможности основаны два улучшения DFM качества топологии.
В приложении указана статья, где описано, как можно улучшать DFM. Для этого вносят дополнительные ограничения, которые описывают DFM правила. В улучшение качества входят также и различные выравнивания сток/исток контактов, а так же просто контактов внутри их металлического контура. После этапа сжатия контакты, которые не попали в критический путь, имеют свободный интервал, поэтому над ними можно проводить различные улучшения. Приведем пример. На рисунке 27 представлена топология стандартной ячейки с критическим путем, который не включает контакты.
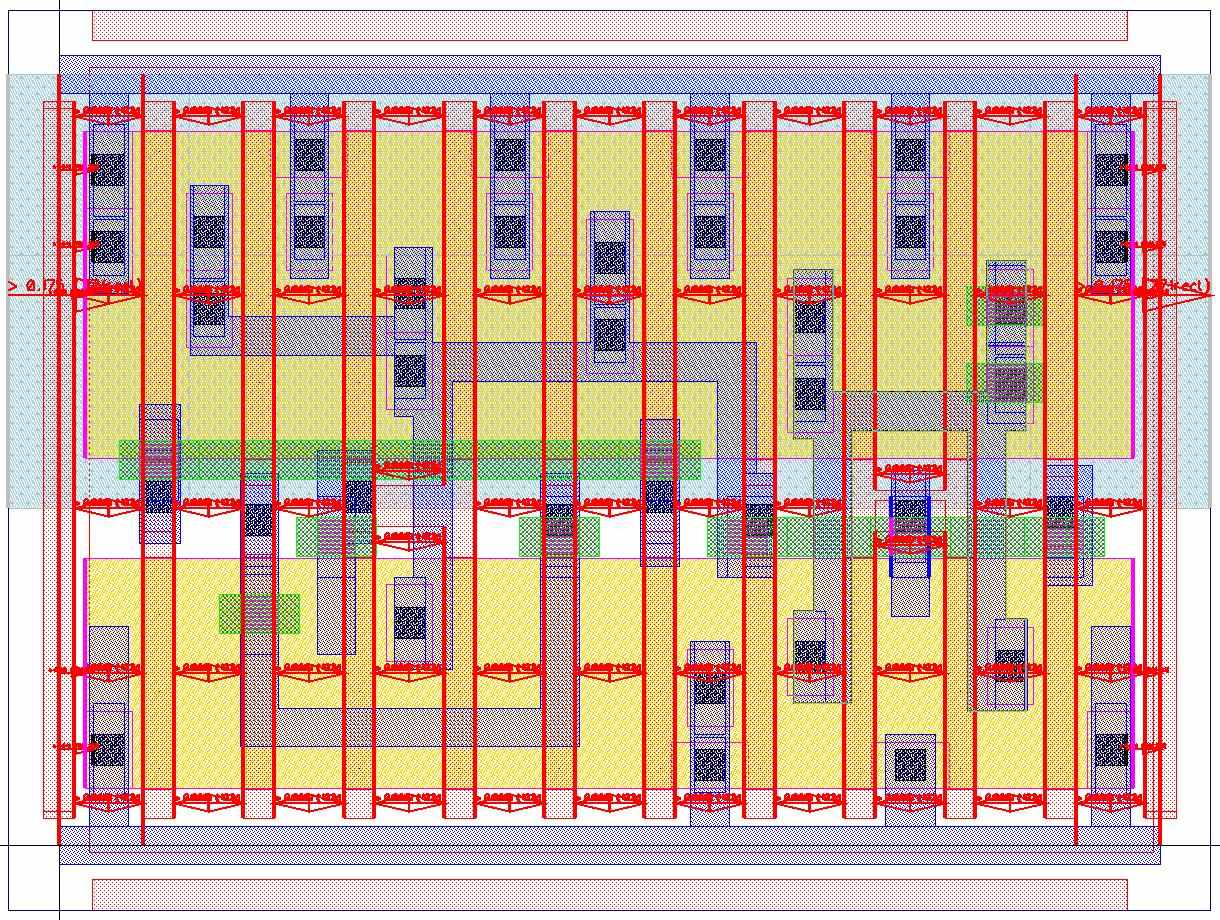
Рис. 21 Пример критического пути, который не включает контакты.
Поэтому положение контактов можно задать любое в пределах свободного интервала.
2.4.1Выравнивание сток/исток контактов
Рассмотрим контакты, которые находятся между двумя затворами. Если они равно удалены от каждого затвора, то фронты этих транзисторов одинаковые (при прочих равных условиях, такие как длинна и ширина транзистора). Поэтому одним из DFM правил является выравнивание контактов между затворами.
Для выполнения этого правила можно воспользоваться нашей функцией, и пытаться сохранить расстояния, указанные стрелками:
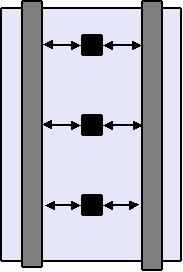
Рис. 22 Расстояния для сохранения при ыравнивании сток/исток контактов.
Первоначально нужно вычислить правильные значения d. Вычислять можно по следующей формуле:
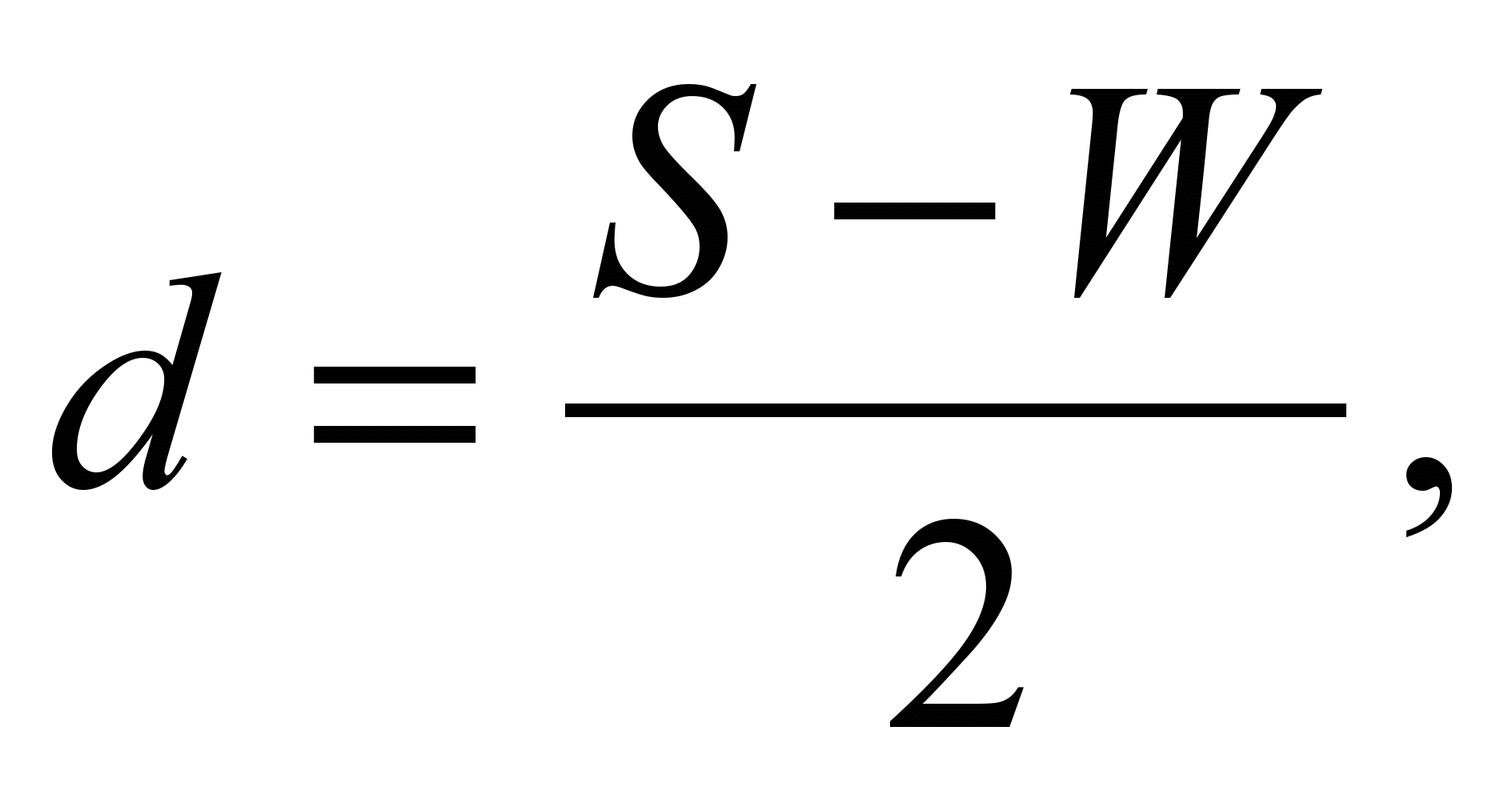где S – расстояние между затворами, а W – это ширина контактного окна. Для выравнивания каждого контакта требуется две конструкции в граф ограничений: одна для расстояния от левого затвора до контакта и вторая – от правой стороны контакта до правого затвора. Расстояния, которые минимизируются, равные в обоих случаях, поэтому можно ограничиться одной конструкции в графе для одного из расстояний.
2.4.2Выравнивание контактов внутри топологических контуров
Вторым примером выравнивания – это центрирование контактов внутри топологических контуров. Необходимо это для того чтобы повысить выход годных. На рис. 29 a) показан пример не выровненного контакта и b) – выровненного
Рис. 23 Пример расположения контактов.
В этом случает необходимо выровнять сначала в Y - направлении контакт в одном из контуров, когда сжатие проходим по Y-направлению, а затем по X-направлению, в другом контуре, описанным выше способом.