Задача минимизации длин проводников 21

Вид материала

Содержание

1.2Алгоритмы сжатия
Рис. 3 1D сжатие
Рис. 4 2D сжатие
1.3Графо-теоретический подход.
1.3.1Построение графа ограничений.
Рис. 7 Пример распространения тени.
Рис. 8 Пример сканирующей линии.
1.3.2Анализ критического пути.
1.3.3Положительные циклы.
Рис. 10 Пример положительного цикла.

Подобный материал:

1 2 3 4 5 6 7 8 9

1.2Алгоритмы сжатия

Алгоритмы сжатия могут быть классифицированы по трем различным критериям. В первом случае классификация основана на способе движения объектов. Таким образом, алгоритмы можно разделить на: одномерные(1D), полуторамерные (1D5) и двумерные(2D).

При 1D сжатии объекты движутся только в X или Y направлении, следовательно, только одна координата объекта изменяется в процессе сжатия. Обычно 1D-сжатие последовательно выполняется для X и Y направлений (Рис. 3). Данные операции повторяются до тех пор, пока размер топологии уменьшается.

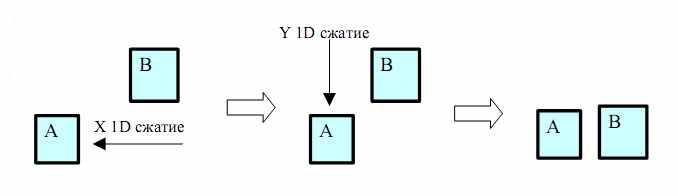
Рис. 3 1D сжатие

При 2D сжатии элементы топологии могут двигаться одновременно в обоих X и Y направлениях. Следовательно, обе координаты объекта изменяются одновременно (Рис. 4).

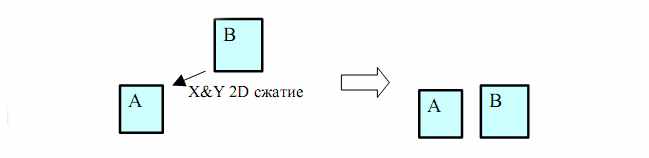
Рис. 4 2D сжатие

Известны 1D алгоритмы, решающие задачу сжатия за полиномиальное время [2], но они не обеспечивают необходимого качества, а 2D сжатие является NP-полной задачей [2], что накладывает ограничения на размерность. Таким образом, с увеличением степени интеграции и появлением сложных технологических правил широкое распространение получили различные эвристические методы. Данные методы не находят оптимального решения, но все таки используют два направления для решения задачи. Они получили название полуторамерных (1.5D). Здесь сжатие происходит в одном (основном) направлении. Главная цель - уменьшить размер топологии в этом направлении. Однако в процессе сжатия возможно изменение координат объектов в другом (ортогональном) направлении.

Второй критерий классификации основан на способе вычисления минимального расстояния между объектами топологии. Здесь существует два класса методов: сжатие, основанное на графе ограничений и на виртуальной сетке.

При использовании графа ограничений связность объектов топологии и технологические правила между ними описываются с помощью линейных неравенств, моделируемых с помощью взвешенного направленного графа (графа ограничений). Этот граф используется для вычисления минимально возможных координат элементов топологии.

С другой стороны, использование виртуальной сетки предполагает, что топология нарисована на сетке. Каждый элемент рассматривается вместе с его линией сетки. При сжатии линия сетки перемещается вместе со всеми элементами, связанными с ней. Минимальная позиция каждой сетки зависит от ее элементов. Преимущество этого метода в том, что он прост и может быть легко реализован. Однако, он не позволяет получить такой плотности топологии, как графовый подход.

Последний критерий - использование иерархии при сжатии. Если сжатие происходит на различных уровнях иерархии, то такой подход называется иерархическим. Алгоритмы, которые раскрывают все уровни иерархии, называются неиерархическими. При иерархическом сжатии размерность решаемой задачи существенно снижается, но решение получается неоптимальным. При полном раскрытии иерархии сильно возрастает размерность задачи и трудно восстановить иерархию после сжатия, что может быть нежелательно.

1.3Графо-теоретический подход.

Одномерное сжатие на основе графа ограничений состоит из шагов, показанных на Рис. 5.

Рис. 5 Алгоритм одномерного сжатия на основе графа ограничений.

Граф ограничений для задачи сжатия - это направленный, взвешенный граф G=(V, E) , где V= {V_i}- множество вершин; E= {E_j} - множество ребер.

Каждая вершина V_i графа представляет некоторый объект топологии и характеризуется его координатой, которая равна X или Y координате объекта в зависимости от направления графа. Граф также содержит две дополнительные вершины Source и Sink. Source - это вершина, которая не имеет входящих ребер, а Sink - выходящих. Source и Sink представляют воображаемые границы топологии.

Ребро описывает множество ограничений между парой объектов и имеет длину L, равную величине максимального ограничения. Существует два типа ограничений: минимального расстояния и связности. Первое используется для достижения минимального расстояния между объектами топологии, а второе для обеспечения связности. Если от объекта А к объекту В есть ограничение на минимальное расстояние длиной L_AB в направлении X (Рис. 6а) ), то

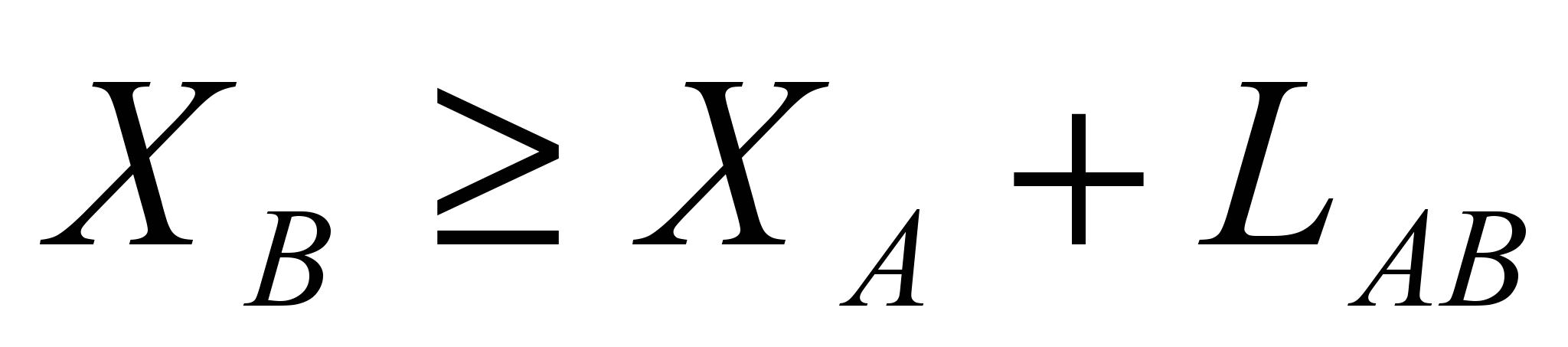(1)

Связность накладывает ограничение на расстояние между объектами и бывает двух видов:

провод-терминал (Рис. 6б)): ограничивает максимальное расстояние между центрами объектов. Если провод W не должен смещаться от терминала T дальше, чем на L_WT, то это описывается неравенствами:

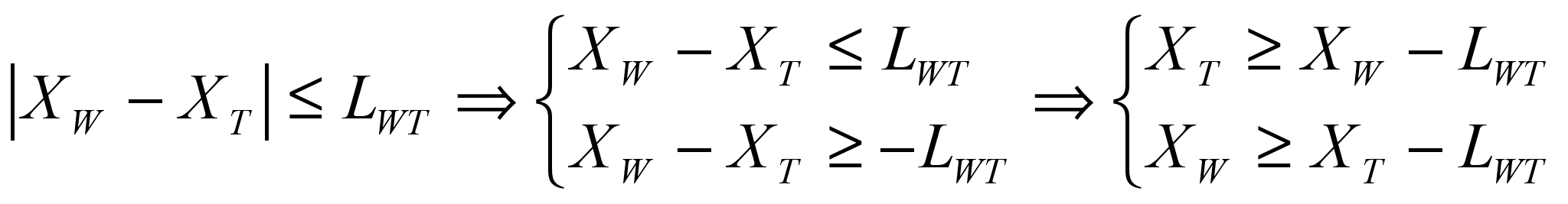(2)

терминал-терминал (Рис. 6в)): фиксируется расстояние между парой терминалов. Например, если терминалы S и D должны быть на расстоянии L_SD, то это описывается неравенствами:

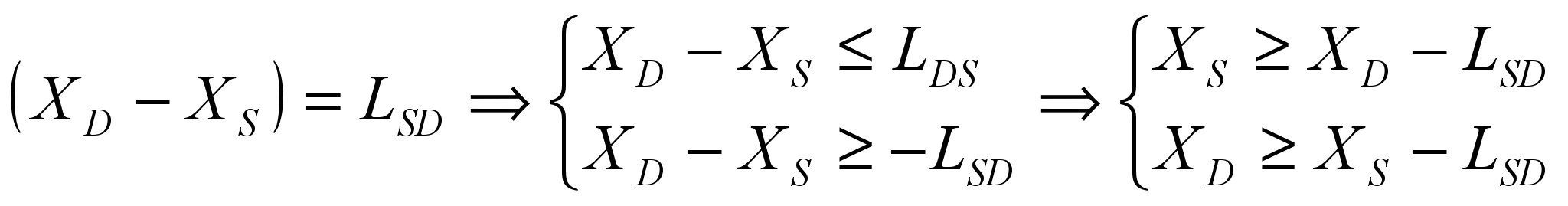(3)

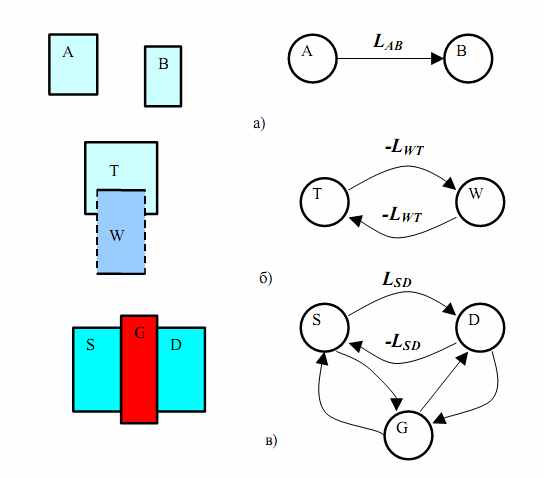
Рис. 6 Виды ограничений: а) мин. расстояния; б) связность провод-терминал; в) связность терминал-терминал (прибор)

1.3.1Построение графа ограничений.

Построение графа ограничений можно разделить на два этапа: первый - построение вершин и второй - ребер.

При построении вершин для заданного направления рассматриваются только элементы топологии, имеющие фиксированный размер в этом направлении. Каждому такому объекту соответствует вершина в графе. Координата вершины равна координате точки привязки объекта.

При построении ребер сначала создаются ограничения связности. Для каждой связи в топологии строятся ребра в соответствии с формулами (2) или (3). Далее строятся ограничения минимального расстояния в соответствии с (1). Создание ребер вносит основной вклад во время работы алгоритма одномерного сжатия. Его сложность равна O(n²), где n - количество объектов топологии. В худшем случае строятся ребра между каждой парой объектов, в то время как используется только их малое подмножество. Существует несколько эффективных методов построения графа ограничений: «Теневой Алгоритм (Shadow-Propagation Algorithm)» [1], средняя сложность которого O(n^1.5), и «Алгоритм Сканирующей Линии (Scanline Algorithm)» [1], сложность которого в худшем случае O(n²), но реально O(n), не считая сортировки.

Теневой алгоритм широко используется при построении графа ограничений. Каждый объект отбрасывает тень в направлении сжатия (Рис. 7). Обычно тень расширяют с двух сторон на величину ограничения. Если тень упирается в другой объект топологии, то добавляется ребро в граф ограничений и из фронта тени удаляется фрагмент, соответствующий препятствию. Процесс продолжается до тех пор, пока не удалится вся тень. Данный алгоритм выполняется для каждого объекта топологии.

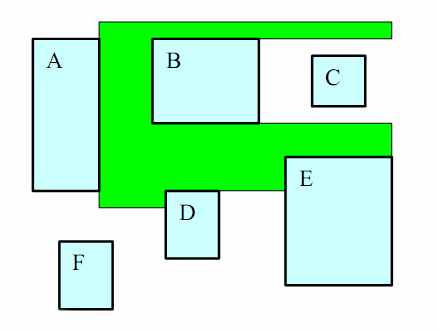
Рис. 7 Пример распространения тени.

Алгоритм Сканирующей Линии также широко применим. В данном методе воображаемая горизонтальная (для X-сжатия) линия сканирует топологию снизу вверх, перемещаясь по нижним и верхним границам элементов (Рис. 8). Сканирующая линия содержит множество элементов, пересекаемых линией и отсортированных по не убыванию X координаты. Добавление элемента в линию происходит, как только линия доходит до нижней его границы. После добавления элемента строятся ограничения со всеми элементами линии. При этом учитывается порядок элементов линии. Когда линия доходит до верхней границы элемента он удаляется из нее. Для удобства сканирования используются два списка элементов топологии. Первый отсортирован по не убыванию нижних границ, а второй - верхних.

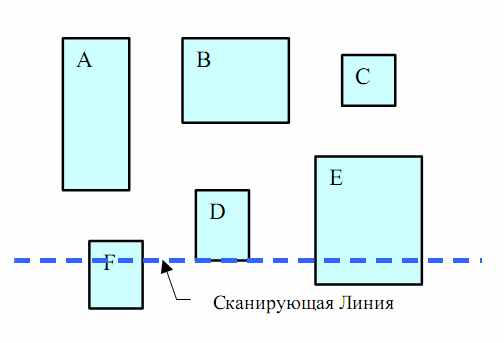
Рис. 8 Пример сканирующей линии.

Алгоритм сканирующей линии создает много избыточных ребер, которые не влияют на длиннейшие пути от Source до каждой вершины графа. Удаление таких ребер не изменит эти пути в графе ограничений. Рассмотрим пример на Рис. 9. Если

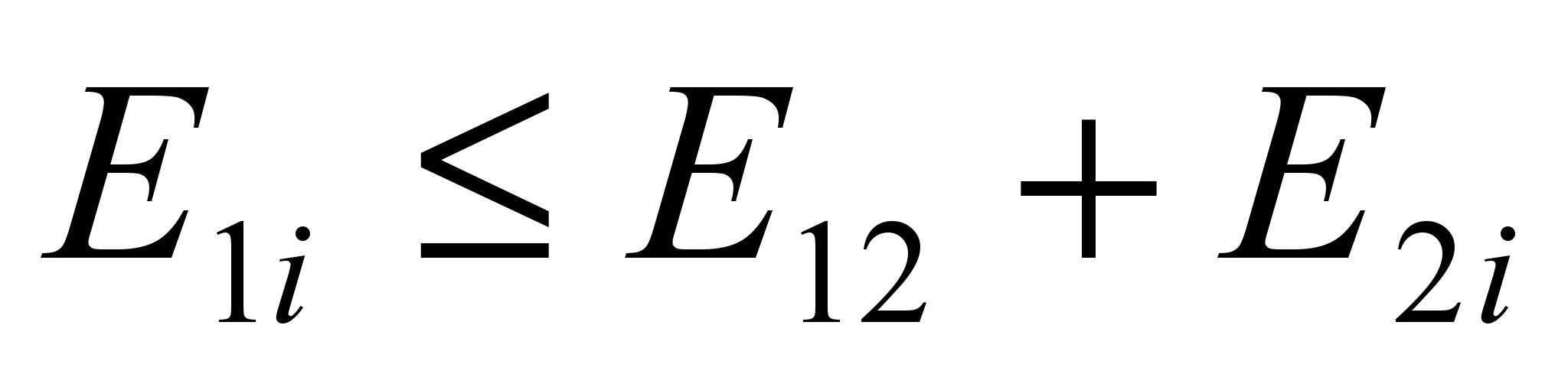, то ребро Е_1i - избыточное и может быть удалено.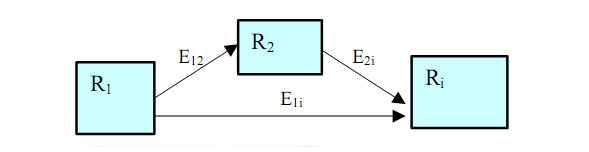

Рис. 9 Пример избыточного ребра

В общем случае ребро называется избыточным, если между двумя вершинами ребра существует путь, не содержащий данного ребра и его длина больше веса ребра. В теории графов такие ребра называют транзитивными. Удаление избыточных ребер значительно сокращает время работы последующих алгоритмов.

1.3.2Анализ критического пути.

Следующим шагом после построения графа ограничений является определение длиннейшего (критического) пути в графе. Основная цель одномерного сжатия - уменьшить размер топологии в направлении сжатия. Задача определения минимального размера эквивалентна задаче нахождения длиннейшего пути в граф. Если вершину Source поставить в нулевую точку, то величина длиннейшего пути от Source до некоторой вершины и будет ее минимально возможной координатой. Множество ребер, которые определяют минимальное расстояние между вершинами Source и Sink, формируют критический путь, а вершины и ребра данного пути называются критическими.

Вершины, которые не являются критическими, могут перемещаться в пределах некоторого интервала, не увеличивая размер топологии. Данный интервал называется Slack. Положение таких вершин может выбираться исходя из других критериев, таких как минимизация длины проводов, повышение выхода годных и т.д.

1.3.3Положительные циклы.

Одна из основных трудностей, с которыми приходится бороться при сжатии с использованием графа ограничений - это положительные циклы. Циклы в графе порождаются ограничениями связности. Если сумма длин всех ребер цикла больше нуля, то данный цикл называется положительным и делает невозможным поиск длиннейшего пути в графе, так как каждый проход по циклу постоянно увеличивает длину этого пути.

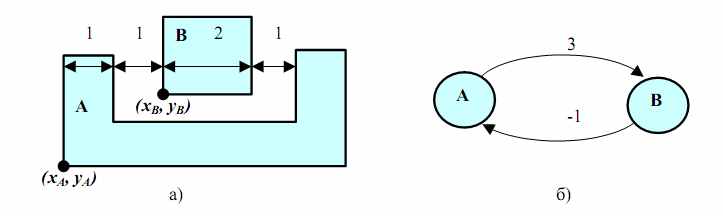
Рис. 10 Пример положительного цикла.

На Рис. 10 a) показан пример топологии, которая порождает положительный цикл в графе ограничений. Если между объектами А и В минимальное расстояние Sp_AB=2 и А - жесткий объект, то

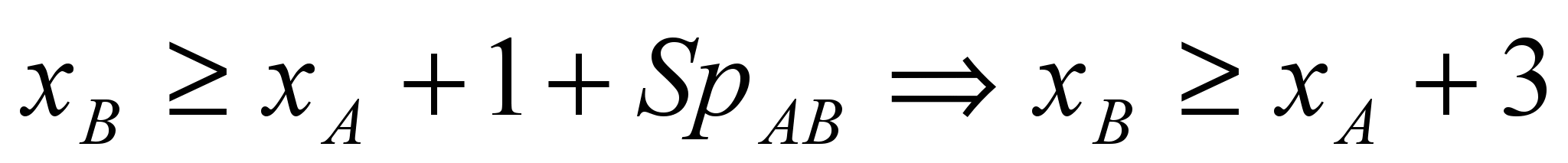и представляет ребро АВ длиной 3. С другой стороны

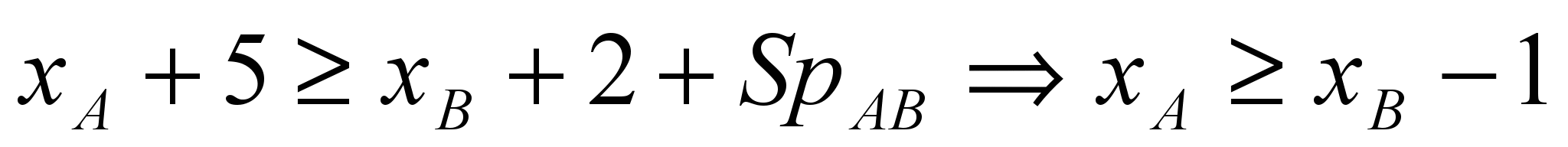и представляет ребро ВА длиной -1. Таким образом, получается положительный цикл длиной 2.

Анализируя публикации, можно выделить следующие методы борьбы с циклами:

Так называемая "заморозка". Все элементы топологии, образующие циклы, рассматриваются как неподвижные относительно друг друга в процессе сжатия и представлены одной вершиной в графе ограничений. Данные элементы помечаются в сжатой топологии для решения конфликта пользователем.
Уменьшение длины ограничений в соответствии с их приоритетом. Обычно корректируется длина ограничений связности. Длина ограничения уменьшается на длину цикла и данное место в топологии помечается стрелкой для информирования пользователя.
Добавление излома на некоторый проводник, который приводит к разбиению соответствующей вершины цикла на две новые, не имеющих ограничений между собой.

Алгоритмы удаления положительных циклов имеют большое значение для сжатия.