0 Распределение "свободных" электронов по энергиям

Вид материала

Документы

Содержание Область примесной проводимости T), то мы получим прямую с накло­ном 1/2k 6 (9) бриллюэна зоны Зонная теория Как и элементарную ячейку, первую зону Бриллюэна можно выбрать и другим способом. Действительно, по определению она должна облад Условия (3.9) означают, что волновая функция должна быть периодична с периодом

Подобный материал:

• ). Закон Дальтона: p=knT=k(n, 43.24kb.
• Те исследуется угловое распределение и энергетический спектр электронов при облучении, 18.67kb.
• Кыргызско-турецкий университет «манас» силлабус, 133.57kb.
• Планирование на предприятии, 524.23kb.
• Программа курса введение. Базовые идеи и материалы для построения структур пониженной, 17.33kb.
• Задачи: дать представление о форме различных орбиталей; обобщив полученные знания,, 82.88kb.
• Оценка влияния создания свободных экономических зон на функционирование региональной, 96.83kb.
• I. результаты, представляемые в доклад президента ран, 1441.88kb.
• Нормальный закон распределения наработки до отказа классическое нормальное распределение, 68.45kb.
• Конспект лекций по курсу «Банковское дело» содержание: Тема кредитная система, 1283.92kb.

Область примесной проводимости

Предположим, что температура недостаточно высока для того, чтобы в заметном количестве наблюдались пере­бросы электронов из заполненной зоны, то есть что электроны в зоне проводимости появляются в основном за счет пере­ходов с примесных уровней, а числом дырок в заполненной зоне мы можем пренебречь. Тогда уравнение (4.39) заме­няется более простым:

n + n_d = N_d (4.41)

или согласно (4.35) и (4.38)

[2(2m_nkT)^3/2/h³]e^–/kT + N_d/[e^{– (1+m)/kT} + 1] (4.42)


Уравнение (4.42) – уже квадратное уравнение относи­тельно е^–/kT . Решая его, получаем

 = – ₁ + kTln{} (4.43)

где {} = 1/2 {[1 + 2e^1/kTN_dh³/(2m_nkT)^3/2]^1/2 – 1}

Выражение (4.43) все еще слишком сложно для его непосредственной интерпретации, поэтому рассмотрим его предельные значения в различных интервалах температур.


Область низких температур:

e^1/kT >> [2(2m_nkT)^3/2/h³]e^/kT (4.44)


Пренебрегая единицами под знаком логарифма, полу­чаем

  –₁/2 + kTln[N_dh³/2(2m_nkT)^3/2]^1/2 (4.45)

В
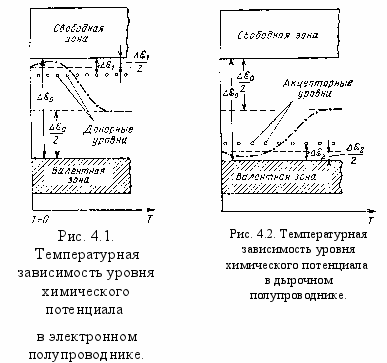
ыражение (4.45) показывает, что при абсолютном нуле температуры уровень химического потенциала проходит строго посредине между дном запрещенной зоны и донор­ными уровнями.

Второй член в (4.45) при низких температуpax [то есть пока (2m_nkT)^3/2 < N_dh³] положительный, а при более высоких становится отрицательным. Поэтому уро­вень химического потенциала сначала поднимается, а затем начинает опускаться (рис. 4.1).

Подставляя (4.45) в (4.35), получаем концентрацию свободных электронов:

n = (2N_d)^1/2[(2m_nkT)^3/4/h^3/2]e^{–1/2kT} = Ae^{–1/2kT}, (4.46)

где А = (2N_d)^1/2[(2m_nkT)^3/4/h³] – величина, слабо зависящая от температуры (по сравнению со вторым экспоненциальным множителем). Выражение (4.46) показывает, что (в этом интервале температур) концентрация электронов в зоне проводимости растет экспоненциально с ростом температуры. Прологарифмировав (4.46), получим

lnn = lnA – ₁/2k(1/T). (4.47)

Следовательно, если мы будем на графике отклады­вать по оси ординат In л, а по оси абсцисс – обратную температуру (1/ T), то мы получим прямую с накло­ном ₁/2k.

Область «высоких» температур:

e^1/kT << [2(2m_nkT)^3/2/h³]e^/kT

Термин «высокие температуры» здесь следует прини­мать лишь в смысле выполнения неравенства (4.48), но мы по-прежнему будем предполагать, что собствен­ная проводимость еще не играет существенной роли. Учитывая (4.48) и разлагая радикал в выражении (4.43) в ряд, получаем

  kTln[N_dh³/2(2m_nkT)^3/2] (4.49)

Согласно (4.48) и (4.49) в этом интервале температур уровень химического потенциала уже спустился ниже донорных уровней, и, следовательно, почти все они должны быть пусты.

Действительно, подставляя (4.49) в (4.35), получаем

n = N_d,

то есть все (или точнее почти все, так как мы все время поль­зуемся приближенными формулами) электроны перешли в зону проводимости. Концентрация электронов проводи­мости в этом интервале температур будет оставаться постоян­ной, что соответствует горизонтальному участку кривой рис. 1.7.

Заметим в заключение, что совершенно аналогичные выводы можно получить для примесного дырочного полу­проводника. В этом случае в области низких температур

'  ₁/2 – kTln[N_ah³/2(2m_pkT)^3/2] (4.50)

где ₂ – энергия, необходимая для заброса электрона из заполненной зоны на акцепторный уровень, то есть уро­вень химического потенциала проходит примерно посре­дине между верхним краем валентной зоны и акцепторным уровнем (рис. 4.2). При этом концентрация дырок меняется экспоненциально:

p = (2N_a)^1/2[(2m_pkT)^3/4/h^3/2]e^{–2/2kT} = Be^{–2/2kT}, (4.51)

В области более высоких температур уровень химиче­ского потенциала поднимается выше акцепторных уровней, и все они в силу этого оказываются забитыми электронами, а число дырок в заполненной зоне становится постоянным:

p = Na.

При дальнейшем подъеме температур и в случае элек­тронного и в случае дырочного полупроводника основную роль начинает играть собственная проводимость.


6

(3) ЗОННАЯ ТЕОРИЯ (ФЭС, т.2, с.86-93)






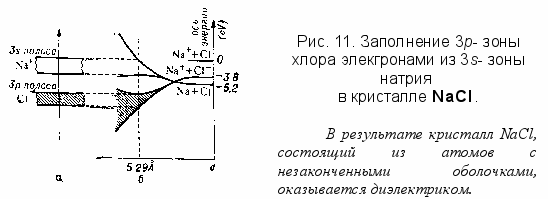
6 (9) БРИЛЛЮЭНА ЗОНЫ (ФЭС, т.1, с.210)


БРИЛЛЮЭНА ЗОНЫ – области k- пространства, внутри которых энергия электрона в кристаллической ре­шетке может изменяться квазинепрерывно; на граниwах зоны Бриллюэна. энергия электрона претерпевает разрыв. Ко­ординатами k-пространства k_x, k_y, k_z являются компо­ненты волнового вектора k, характеризующего стацио­нарные одноэлектронные волновые ф-ции в кристалле:

_k(r) = u_k(r)e^ikr, H_k = (k)_k,

где i – мнимая единица;

H и  – оператор Гамиль­тона и собственное значение энергии электрона в кристалле;

r – радиус-вектор электрона.

Форма концентрических многогранников, служащих границами зоны Бриллюэна, определяется симметрией кристал­лической решетки и тесно связана с условиями дифрак­ционных максимумов рентгеновых лучей в кристалле (уравнением Вульфа – Брэгга).

См. Зонная теория

ЗОНЫ БРИЛЛЮЭНА

(Бонч-Бруевич и Калашников, Физика полупроводников, М.1977, страницы 94100)


Этот материал полезен тем, кого привлекает академический способ изложе­ния и вообще теория. А еще интереснее оказался бы Ансельм А.И., Введение в теорию полупроводников, М.,1962.

Что же касается тех, кому милее экспериментальная физика, тоже может успешно воспользоваться этим материалом, а именно: если вдруг одолеет смертельная бессонница и никакие транквилизаторы не помогают уснуть, то нет в мире лучшего снотворного, чем это чтиво. В.Г.


§ 3. Зоны Бриллюэна

Введенный в предыдущем параграфе вектор квазиимпульса определяется равенствами (2.14)⁴⁾ и (2.17)⁵⁾. Комбинируя их, мы полу­чаем

(r + a_n) =  (r)exp[(i/)pa_n]. (3.1)

Таким образом, вектор p (или k = p/) характеризует закон преобразования волновой функции электрона при сдвиге ее аргумента на какой-либо вектор решетки. Разным собственным функ­циям соответствуют, вообще говоря, различные значения квази­импульса (квазиволнового вектора). Поэтому компоненты его (как и компоненты импульса в случае свободного электрона) следует рассматривать как квантовые числа, характеризующие данное ста­ционарное состояние. Однако, в отличие от компонент импульса и от квантовых чисел, встречающихся в теории атома, квазиимпульс определяется в принципе неоднозначно. Действительно, обозначим через с вектор, скалярное произведение которого на a_n есть целое кратное 2p:

a_nc = 2p  (целое число). (3.2)

Очевидно, векторы p и p + c, будучи подставлены в правую часть (3.1), дают один и тот же результат. Но равенство (3.1) есть единст­венное условие, определяющее квазиимпульс. Следовательно, век­торы p и p + c физически эквива­лентны: оба они определяют одно и то же преобразование волновой функции.

Нетрудно найти явный вид вектора p. Для этого следует лишь ввести понятие обратной решетки. Основные векторы последней b₁, b₂, b₃, определяются равенствами

b₁ = 2[a₂xa₃]/V₀, b₁ = 2[a₃xa₁]/V₀, b₁ = 2[a₁xa₂]/V₀, (3.3)

где V₀ = |(a₁[a₂a₃]| есть объем параллелепипеда, построенного на векторах a₁, a₂, a₃ (объем элементарной ячейки). В частности, в простой кубической решетке, когда a₁ = a₁ = a₂ = a_з = а и b₁ = b₂ = b₃ = b, мы имеем

b = 2/a. (3.3')

Очевидно, векторы b₁, b₂, b₃ имеют размерность обратной длины. На основных векторах b₁, b₂, b₃ можно построить периодическую решетку. Она и называется обратной (по отношению к прямой ре­шетке данного кристалла).

Произвольный вектор обратной решетки имеет вид

b_т = m₁b₁ + m₂b₂ + m₃b₃, (3.4)

где m₁, m₂, m₃ – положительные или отрицательные целые числа или нули (при этомm₁, m₂, m₃ не равны нулю одновременно), т = {m₁, m₂, m₃}.

Элементарная ячейка обратной решетки представляет собой параллелепипед, построенный на векторах b₁, b₂, b₃.

«Объем» этого параллелепипеда равен |(b₁[b₂b₃])| (разумеется, он имеет размерность обратного объема). Подставляя сюда формулы (3.3) для b₁, b₂, b₃ и раскрывая получающееся произведение, находим

|(b₁[b₂b₃])| = (2)³/V₀. (3.5)

Как и в случае прямой решетки, выбор элементарной ячейки в обратной решетке неоднозначен и определяется соображениями удобства.

Другой способ построения элементарной ячейки состоит в сле­дующем. Какой-то узел обратной решетки выбирают в качестве начала координат и соединяют его прямыми линиями с ближайшими к нему узлами. Через середины этих линий перпендикулярно к ним проводят плоскости. В качестве элементарной ячейки обратной решетки можно выбрать наименьший многогранник, ограниченный так построенными плоскостями и содержащий внутри себя начало координат. Этот многогранник называется ячейкой Вигнера – Зейтца.

Такие многогранники можно построить около любого узла ре­шетки; при этом они не перекрываются и совокупность их заполняет все обратное пространство. Отсюда следует, что объем одного много­гранника действительно равен (2)³/V₀. как это и должно быть.

В отличие от параллелепипеда, построенного на векторах b₁, b₂, b₃, элементарная ячейка» выбранная указанным только что образом» обладает всеми свойствами симметрии обратной решетки. Из определения (3.3) вытекают равенства

a₁b₁= a₂b₂= a₃b₃ = 2,

a_b_ = 0,    (,  = 1,2,3).

Умножим теперь произвольный вектор решетки (II.1.1) на век­тор обратной решетки (3.4). Пользуясь соотношениями (3.6), мы получаем

a_nb_m = (n₁m₁ + n₂m₂ + n₃m₃)2.

В скобках в правой части этого равенства стоит целое число, и, сле­довательно, вектор c, удовлетворяющий условию (3.2), можно записать в виде

c = b_m. (3.7)

Итак, квазиимпульс определен лишь с точностью до вектора обратной решетки, умноженного на . Это обстоятельство позволяет ограничить изменение компонент квазиимпульса конечной областью, исчерпывающей все физически неэквивалентные их значения. Такая область – совокупность всех физически неэквивалентных значений квазиимпульса – называется зоной Бриллюэна. В силу произвольности вектора b_т в (3.7) выбор ее неоднозначен. Так, можно выбрать в качестве зоны Бриллюэна область, определяемую неравенствами

–  < pa₁  ,

–  < pa₂  , (3.8)

–  < pa₃  ,

Эти неравенства определяют некоторый параллелепипед в p-пространстве, содержащий в себе начало координат. Его называют первой зоной Бриллюэна.

Можно определить первую зону Бриллюэна и для компонент квазиволнового вектора k: надо лишь заменить p на k в неравен­ствах (3.8), опустив множители . Квазиимпульс (или квазиволно­вой вектор), изменяющийся в пределах первой зоны Бриллюэна, называется приведенным. В частности, в простой кубической ре­шетке векторы a₁, a₂, a₃ одинаковы по величине (равной постоянной решетки a) и направлены по трем взаимно перпендикулярным осям куба. Выбирая эти оси в качестве координатных, получаем из (3.8) для данного частного случая

– p/a < p_  /a,  = x, y, z. (3.8')

Первая зона Бриллюэна здесь представляет собой куб объема

(2)³/V₀ = (2)³/a³.

в k-пространстве соответствующий объем равен (2)³/V₀.

Полученное только что выражение для объема первой зоны Бриллюэна справедливо и для произвольной решетки. Действительно, интересующий нас объем дается интегралом

J = dp_xdp_ydp_z,

взятым по области, определяемой неравенствами (3.8). Для вычисления этого интеграла удобно ввести переменные

₁ = (1/)(pa₁), ₂ = (1/)(pa₂), ₃ = (1/)(pa₃).

Якобиан перехода от переменных ₁, ₂, ₃ к переменным p_x, p_y, p_z пред­став­ляет собой детерминант [1]

d1/dpx d2/dpx d3/dpx	=	a1x a2x a3x	=	(a1[a2a3])  3	= V0/3
d1/dpy d2/dpy d3/dpy		a1y a2y a3y
d1/dpz d2/dpz d3/dpz		a1z a2z a3z

d₁d₂ d₃ = (V₀/³)dp_xdp_уdp_z.

и, следовательно,

J = (³/V₀)_–^d_–^d_–^d_³/V₀

Выбирая другие периоды p_x, p_y, p_z, мы получим вторую, третью и т. д. зоны Бриллюэна. Можно доказать [М6], что объемы их всех одинаковы и равны (2)³/V₀.

Вспоминая теперь равенство (3.5), видим, что объем зоны Брил-люэна равен объему элементарной ячейки в обратной решетке (умноженному на ³, если речь идет о p-пространстве).

Как и элементарную ячейку, первую зону Бриллюэна можно выбрать и другим способом. Действительно, по определению она должна обладать следующими свойствами:

а) внутри нее должна содержаться точка k = 0;

б) любые два вектора k, входящие в нее, могут отличаться друг от друга не более чем на (b₁ + b₂ + b₃), и в) объем ее равен (2)³/V₀.

Этими свойствами обладает ячейка Вигнера – Зейтца. Она и представляет собой первую зону Бриллюэна. В дальнейшем мы будем пользоваться этим определением.

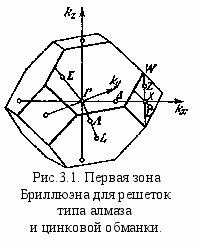
Таким образом, зона Бриллюэ­на есть чисто геометрическое по­нятие: форма ее зависит только от структуры решетки, но не от природы действующих в ней сил. Более того, как видно из предыду­щего, зона Бриллюэна определяет­ся только основными векторами решетки. Следовательно, она одна и та же как для простых, так и для базисных решеток одной и той же сингонии, например для простой гранецентрированной ре­шетки и для решетки типа алмаза.

На рис.3.1 изображена первая зона Бриллюэна для решеток типа алмаза и цинковой обманки. Некоторые точки в ней представляют особый интерес при исследовании поведения электронов и дырок. Это – «точки симметрии», обладающие тем свойством, что они переходят сами в себя при некоторых преобразованиях симметрии, допускаемых в данной решетке. К числу названных точек отно­сятся центр первой зоны Бриллюэна (то есть начало координат в k-про­странстве), центры ее граней или ребер, точки на осях – линиях, соединяющих центр зоны с центрами граней или ребер, и т. д.

Их принято обозначать большими греческими или латинскими буквами, которые и указаны на рисунках. Так, точка Г есть не что иное, как центр первой зоны Бриллюэна, и т. д.

Неоднозначность квазиимпульса есть специфическое свойство электрона, движущегося в периодическом поле.

Она составляет наиболее резкое различие между квазиимпульсом и импульсом: последний определен однозначно, и компоненты его p_x, p_y, p_z изме­няются в пределах от –  до + . Заметим, что мы можем фор­мально убедиться в этом, требуя, как и в конце предыдущего пара­графа, инвариантности системы относительно сдвига на любой вектор. Действительно, в этом случае точки, бесконечно близкие друг к другу, также являются эквивалентными, т. е. «постоянная решетки» a сколь угодно мала. Устремляя a к нулю, видим из (3.8'), что компоненты p_x, p_y, p_z изменяются в пределах от –  до + . Объем «зоны Бриллюэна» при этом также оказывается бесконечным: она представляет собой просто все импульсное пространство.

Неравенства (3.8) определяют пределы изменения компонент квазиимпульса, но ничего не говорят о физически дозволенных их значениях. Таковые определяются граничными условиями, накладываемыми на волновую функцию . Строго говоря, гранич­ные условия призваны отражать физическую ситуацию на поверх­ности образца. Эта ситуация определяется характером сил, дейст­вующих на электроны. Однако все силы взаимодействия, с которыми мы имеем дело, более или менее быстро убывают с расстоянием. Следовательно, условия на поверхности не могут сколько-нибудь заметно влиять на поведение электронов в глубине кристалла, если размеры его достаточно велики. Поэтому для определения возможных значений квазиимпульса в большом образце нет необхо­димости рассматривать истинную (далеко не простую) картину поверхностных явлений, а можно воспользоваться следующим искусственным приемом. Выделим прежде всего «внутреннюю область» кристалла, определив ее как объем, в котором не сказы­ваются специфические эффекты, связанные с наличием поверхности. Внутреннюю область разобьем на ряд достаточно больших частей, например кубов со стороной L. Длина L должна значительно пре­вышать все «физические» длины, фигурирующие в задаче, – посто­янную решетки, длину волны электрона, длину свободного про­бега и т. д.; в остальном значение L произвольно. Поскольку раз­личные кубы ничем не выделены, естественно потребовать, чтобы значения волновой функции в соответственных (отстоящих друг от друга на расстояние L) точках соседних кубов были одинако­выми:

 (x, y, z) =  (x+L, y, z) = ... =  (x+L, y+L, z+L). (3.9)

Равенства (3.9) позволяют ограничиться изучением движения элек­тронов в пределах только одного куба, рассматривая его как «крис­талл»; все, что в нем происходит, будет повторяться и в других кубах. Таким образом, оказывается возможным формально ввести в задачу «размеры кристалла», не интересуясь в то же время явле­ниями на его поверхности⁶⁾.

Условия (3.9) означают, что волновая функция должна быть периодична с периодом L. Соответственно и сами условия (3.9) называются условиями периодичности (или условиями Кармана – Борна). Сам куб со стороной L называется кубом периодичности (употребляют также названия «фундаментальный объем», «основной объем» или «основная область»).

Поскольку длина L сколь угодно велика, мы вправе считать L целым кратным a, где a — постоянная решетки по соответствующему направлению.

Поэтому, накладывая условия (3.9) на функцию (2.15) и принимая во внимание свойство периодичности u_k(r) (2.16), мы получаем

exp[i(k_xx + k_yy + k_zz)]u_k(x, y, z) =

= exp[ik_x(x + L) + ik_y (y + L) + ik_z(z + L)]u_k[(x+L), (y+L), (z+L)] =

= exp[ik_x(x + L) + ik_y (y + L) + ik_z(z + L)]u_k(x, y, z).

Отсюда

k_x = (2/L)n_x, k_x = (2/L)n_y, k_x = (2/L)n_z, (3.10)

где n_x, n_y, n_z — положительные или отрицательные целые числа (ограниченные условиями (3.8)) или нули.

Соответственно

p_x = (2/L)n_x, p_y = (2/L)n_y, p_z = (2/L)n_z. (3.10’)

Таким образом, значения компонент квазиволнового вектора (или квазиимпульса) образуют дискретную совокупность. Разно­сти между соседними значениями их, однако, весьма малы (равны соответственно 2/L и 2/L . По этой причине указанная, дискрет­ность не проявляется в наблюдаемых на опыте электрических и оптических явлениях. Спектр такого типа называется квазинепре­рывным.