0 Распределение "свободных" электронов по энергиям

Вид материала

Документы

Содержание Рассмотрим самым примитивным образом Упругое рассеяние Рассеяние на фононах Рассеяние на заряженных центрах Симметрия атомов, молекул и кристаллов

Подобный материал:

• ). Закон Дальтона: p=knT=k(n, 43.24kb.
• Те исследуется угловое распределение и энергетический спектр электронов при облучении, 18.67kb.
• Кыргызско-турецкий университет «манас» силлабус, 133.57kb.
• Планирование на предприятии, 524.23kb.
• Программа курса введение. Базовые идеи и материалы для построения структур пониженной, 17.33kb.
• Задачи: дать представление о форме различных орбиталей; обобщив полученные знания,, 82.88kb.
• Оценка влияния создания свободных экономических зон на функционирование региональной, 96.83kb.
• I. результаты, представляемые в доклад президента ран, 1441.88kb.
• Нормальный закон распределения наработки до отказа классическое нормальное распределение, 68.45kb.
• Конспект лекций по курсу «Банковское дело» содержание: Тема кредитная система, 1283.92kb.

Рассмотрим самым примитивным образом

роль заряженных центров и фононов.


Неупругое рассеяние происходит на оптических фононах благодаря межэлектронному взаимодействию.

Упругое рассеяние происходит на дефектах и акустических фононах.


Поскольку  = (e/2m)<>, то для определения температурной зависимости подвижности  надо искать, как зависит от температуры <> – среднее время свободного побега.

В свою очередь, <> обусловлено – средней скоростью электронов и < – средней длиной их свободного пробега:

<> = <v>

Согласно примитивной модели Друде, все электроны имеют одинаковую скорость, то есть, v> = v = Const. Поскольку в металлах дрейфовая скорость не может быть соизмеримой с тепловой скоростью, то можно принять: v = v_T + v_D  v_T ~ T^1/2 (из: _{электронов} ~ v² ~ T).

Итак, v ~ T^1/2

Остается оценить <> при рассеянии на фононах и заряженных центрах рассеяния.

Рассеяние на фононах.

Число столкновений электронов на колеблющихся атомах, обозначим его через Z, пропорционально квадрату амплитуды их колебаний A²:

Z ~ A².

В свою очередь, амплитуда колебаний A пропорциональна квадратному корню от температуры:

A ~ T^1/2.

Стало быть: Z ~ T.

Поскольку, чем больше центров рассеяния, тем короче свободный пробег, то:

<_Ф ~ 1/Z ~ 1/T.

Окончательно для рассеяния на фононах <_Ф = <_Ф/v имеем:

<_Ф ~ T^–3/2


Рассеяние на заряженных центрах.

Будем для упрощения считать, что число заряженных центров в металле от температуры не зависит.

Согласно результатам опытов Резерфорда по рассеянию -частиц (отклонение в электростатическом поле) длина свободного пробега пропорциональна четвертой степени скорости частиц:

<> ~ ⁴

Значит, для рассеяния на заряженных центрах (ионах) имеем:

<_И = <_И/v ~ ⁴/v ~ ³ ~ T^3/2

<_И ~ T^3/2

1 (2) СИММЕТРИЯ (Жданов, с.133)


Глава V

СИММЕТРИЯ АТОМОВ, МОЛЕКУЛ И КРИСТАЛЛОВ

§ 1. СИММЕТРИЯ КОНЕЧНЫХ И БЕСКОНЕЧНЫХ ФИГУР

Симметрия³⁾. Операции симметрии.

Волновые функции атома водорода и образуемые из них гибридные вол­новые функции и распределения электронной плотности в атомах обладают симметрией. Симметрия атомов и образуемых ими связей приводит к опре­деленной симметричной структуре молекул и кристаллов. Знание основ учения о симметрии и способов изображения симметрии существенно для понимания и описания структуры молекул и кристаллов и анализа их свойств.

Симметрия какого-либо тела заключается в его свойстве самосовме­щаться в различных своих положениях. Это свойство проявляется в повто­рении частей тела в пространстве.

Симметрия расширяет понятие равенства фигур (А. В. Шубников). Равными можно назвать фигуры, в которых расстояния между соответст­вующими точками одинаковы. Это условие необходимо, но недостаточно для обычного равенства, когда фигуры совмещаются при наложении. Это условие соблюдается также и для правых и левых фигур, которые не сов­мещаются друге другом при наложении (например, правая и левая перчатки, правая и левая молекулы винной кислоты, правый и левый кварц). Подоб­ные фигуры совмещаются только после зеркального отражения, переводя­щего правую фигуру в левую и наоборот. Различие правых нулевых форм молекул и кристаллов проявляется как в структуре, так и в некоторых физи­ческих свойствах и может быть установлено, например, по вращению плос­кости поляризации.

Совмещение разных тел или самосовмещение одного тела

осуществ­ляется с помощью:

• отражений;
  
• поворотов;
  
• инверсий;
  
• параллельных переносов;
  

называемых операциями симмет­рии

или

симметрическими преобразованиями.

Симметрические преобразо­вания являются преобразованиями координат (x, y, z) – (x', y', z') без рас­тяжений, сжатий и сдвигов, то есть такими, при которых расстояния между точками до и после преобразования не изменяются.

Симметрию кристаллов можно описывать двояко. Во-первых, кристаллы представляют собой конечные тела, обладающие анизотропией свойств, что часто проявляется в правильной их форме. В этом случае кристаллы можно заменить многогранниками, имеющими одинаковую с ними симметрию, и описывать их симметрию (с некоторыми ограничениями, рас­сматриваемыми далее) аналогично симметрии атомов и молекул и вообще конечных фигур.

Во-вторых, кристаллы обладают правильными периодиче­скими структурами и их можно рассматривать, как бесконечные тела, само­совмещающиеся при параллельных переносах, кратных периодам структуры.

В этом случае операцией симметрии является параллельный перенос (трансляция), отсутствующий у конечных фигур.

Представление о кристаллах, как о телах, имеющих правильную периодическую структуру, зародилось уже давно и первоначально было получено путем дедукции на основании данных о макроскопических свойствах кристаллов.

Достаточно строгое обос­нование теории решетчатого строения дало изучение симметрии и в первую очередь фе­номенологически установленный закон симметрии кристаллов (стр. 142).

Задолго до по­явления тонких методов исследования и наблюдения атомно-молекулярной структуры вещества Е.С. Федоровым (1890) была создана теория пространственных групп, описы­вающая симметрию атомных структур кристаллов, Веским, но все же косвенным аргументом в пользу решетчатого строения явилось открытие Лауэ (1912) дифракции рентге­новых лучей в кристаллах. Развитие новых микроскопических методов в последнее время позволило наблюдать молекулярную и атомную структуру и увидеть пространственную решетку.


О
перации поворота и параллельного переноса, который можно рас­сматривать как поворот на бесконечно малый угол около бесконечно уда­ленной оси, не меняют типа фигуры. Правая фигура при этих операциях остается правой фигурой. Отражение и инверсия изменяют тип фигуры, превращая правую фигуру в левую. Соответственно операции симметрии можно разделить на две группы: операции I и II рода, не изменяющие и изменяющие тип фигуры.

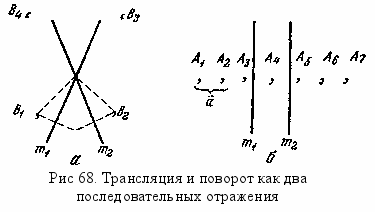
Простейшей операцией симметрии является отражение. Все другие операции симметрии можно свести к отражениям в ряде зеркал. Поворот на угол  эквивалентен отражениям в двух пересекающихся на оси поворота плоскостях, образующих между собой угол ½. При отражениях в калей­доскопе, состоящем из пересекающихся зеркал т₁ и т₂ (рис. 68, а), обра­зуется ряд точек B₁, B₂, B₃, ... , расположенных по кругу и повернутых друг к другу под углами, равными .

Параллельный перенос, определяемый вектором a, эквивалентен отра­жениям в двух плоскостях, перпендикулярных к вектору переноса и уда­ленных друг от друга на ½. При последовательных отражениях в калейдо­скопе, состоящем из параллельных зеркал, образуется прямолинейный пери­одический ряд точек A₁, A₂, A₃, ... (рис. 68, б).

Инверсия в центре симметрии эквивалентна отражениям в трех взаим­но-перпендикулярных зеркалах, проходящих через центр симметрии. Слож­ные операции симметрии образуются сочетанием отражений, поворотов и инверсий, поэтому любые операции симметрии I и II рода можно заменить соответственно четным или нечетным числом отражений.

Симметрию любого тела можно описать с помощью одних операций отражения. Это было выполнено в применении к симметрии кристаллических форм известным русским кристаллографом Ю.В. Вульфом. Однако для большей наглядности удобнее описывать симметрию, пользуясь сложными операциями симметрии.