0 Распределение "свободных" электронов по энергиям

Вид материала

Документы

Содержание Элементы симметрии (с.136)

Подобный материал:

• ). Закон Дальтона: p=knT=k(n, 43.24kb.
• Те исследуется угловое распределение и энергетический спектр электронов при облучении, 18.67kb.
• Кыргызско-турецкий университет «манас» силлабус, 133.57kb.
• Планирование на предприятии, 524.23kb.
• Программа курса введение. Базовые идеи и материалы для построения структур пониженной, 17.33kb.
• Задачи: дать представление о форме различных орбиталей; обобщив полученные знания,, 82.88kb.
• Оценка влияния создания свободных экономических зон на функционирование региональной, 96.83kb.
• I. результаты, представляемые в доклад президента ран, 1441.88kb.
• Нормальный закон распределения наработки до отказа классическое нормальное распределение, 68.45kb.
• Конспект лекций по курсу «Банковское дело» содержание: Тема кредитная система, 1283.92kb.

Элементы симметрии (с.136)

Операции симметрии выполняются с помощью геометрических элемен­тов. называемых элементами симметрии. В трехмерном пространстве такими элементами являются плоскость, прямая, точка, вектор переноса, а также более сложные элементы симметрии, возникающие в результате сочетания указанных элементов. Понятие «элемент симметрии», так же как и «элемен­тарная частица», является условным. Все «элементы» симметрии, кроме зеркальной плоскости, являются сложными. Система единиц (элементов) в учении о симметрии строится по принципу объединения единиц низшего порядка в единицы высшего порядка, на котором основана десятичная и подобные ей системы счета. В табл.21 приведены наиболее употребительные элементы симметрии, указаны их обозначения, даны координаты групп равнозначных точек, возникающих при выполнении операций симметрии, предписываемых элементом симметрии, и кратности. Кратность равна числу равнозначных точек, образуемых элементом симметрии.

Элементарный угол поворота _n для оси симметрии n-го порядка Cn определяется из условия цикличности

_n= 2p/n, n = 1,2.3... (V,1)

Л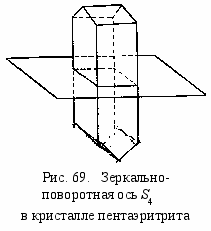юбая прямая является осью симметрии 1-го порядка C₁. Наличие в теле только таких элементов симметрии говорит об отсутствии симметрии. Зеркально-поворотные оси соответствуют повороту около оси и отражению в перпендикулярной плоскости. В осях четного порядка S_2n, как видно на примере кристалла пентаэритрита (рис. 69), имеющего ось S₄, нет ни от­дельно существующей поворотной оси C₄ ни перпендикулярной к ней плос­кости симметрии.

Поворотная ось симметрии вырождается в ось C_n с вдвое пониженной кратностью. Нечетные зеркально-поворотные оси распадаются на поворотную ось и перпендикулярную к ней плоскость S_2n+1 = C_2n+1+ m. Поэтому как самостоятельные элементы симметрии рассматриваются только четные зеркально-поворотные оси S_2n. Группа инверсионных осей эквива­лентна группе зеркально-поворотных осей: S_i = 1 = i; S₄ = 4; S₄= 3.

Отражение и поворот оставляют на месте точки, лежащие соответственно на плоскости и на прямой. Инверсия и операции, с ней связанные (инвер­сионные и зеркально-поворотные оси), оставляют на месте точку тела.

Таблица 21 Операции симметрии, элементы симметрии и их обозначения (с.137)

Операция симметрии	Элемент симметрии	Обозначение		Координаты равнозначных (сим­метричных) точек	Кратность (число равно­значных точек)
		по Шенфлису	между­народ­ное
Отражение в плоскости	плоскость симметрии	Cs	т	xyz; xỹz (плоскость т перпендикулярна оси Y)	2
Отражение в плоскости	плоскость симметрии	Cs	m	x y z; x y z (плоскость m перпендикулярна оси Y)	n
Поворот около оси на угол n	ось симметрии	Cп	п	x y z; xy z (ось C3 совпадает с осью Z)	n
Инверсия в точке	центр сим­метрии	Ci	i =1	xyz; x y z (центр симметрии в на­ чале координат)	2
Поворот около оси и отражение в перпен­дикулярной плоскости	зеркально- поворотная ось	S2n
Поворот около оси и ин­ версия в центре сим­метрии, лежащем на оси	инверсионная ось		n		п
Параллельный перенос	вектор переноса (трансляция) a,b,c			x = та; y = па, z = pa; т, n, p – целые числа	
Отражение в плоскости и перенос параллель­но плоскости	плоскость скольжения		a, b, c п, d		
Поворот около оси и перенос параллельно оси	винтовая ось		nт m =1, 2, ... , n		

Перечисленные операции и элементы симметрии, оставляющие на месте по крайней мере одну точку тела, возможны как в конечных, так и в беско­нечных телах. Кратности этих элементов конечны.

Кратности операций симметрии, связанных с параллельным переносом, равны бесконечности.

Эти операции симметрии не оставляют на месте ни одной точки тела и возможны только в бесконечных телах с периоди­ческой структурой. Последователь­ное применение параллельного пере­носа а к исходной точке, которую на­зовем узлом, приводит к образованию бесконечного, прямолинейного и периодического ряда узлов, положение которых определяется вектором линейной решетки р = та, где а –длина осевого масштаба, а m – любые целые числа, координаты узлов ряда.

Сочетание двух векторов переноса приводит к образованию двухмерной периодической сетки. Положение узлов плоской сетки определяется бинар­ной линейной формой p = та + nb. Сочетание трех некомпланарных век­торов переноса a, b, c приводит к образованию трехмерной бесконечной и периодической сетки, называемой пространственной решет­кой.

Координаты узлов пространствен­ной решетки определяются трехчленной линейной формой

р = та + nb + pc, (V,2)

где [[m, n, p]] – целочисленные коорди­наты узлов.

Сочетание плоскости симметрии с пер­пендикулярным к ней переносом a_n приво­дит к трансляционному размножению пло­скостей симметрии и образованию калейдо­скопа из параллельных зеркал, в котором зеркально-симметричный узел размножается в периодический ряд. При соче­тании отражения с параллельным переносом а возникает новый элемент симме­трии – плоскость скольжения.

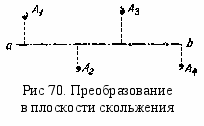
Н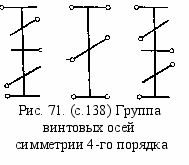а рис. 70 ab – след плоскости скольжения; направление сдвига параллельно плоскости чертежа. Плоскость скольжения приводит к образованию периодического ряда A₁, A₂, A₃, A₄, ... в виде «елочки» с периодом вдоль плоскости скольжения 2a_i. Сочетание поворота со сдвигом, параллельным оси поворота, дает винтовое движение, которому отвечает новый элемент симметрии – винтовая ось. Сдвиги вдоль винтовой оси n-го порядка a_i = (m/n)a, где т = 1 , 2, ... , п. Полный набор винтовых осей n-го порядка равен п, включая поворотную ось, для которой т = 0 (m = п). На рис.71 изображена группа винтовых осей симметрии 4-го порядка. Оси 4₁ и 4₃ – зеркально-симметричные право- и лево- винтовые оси. Ось 4₂ содержит поворотную ось 2.


6 (13) ОБЛАСТЬ ПРИМЕСНОЙ ПРОВОДИМОСТИ (Стильбанс, с.231)