0 Распределение "свободных" электронов по энергиям

Вид материала

Документы

Содержание Введем обозначение В случае большого уровня биполярного возбуждения По виду передачи энергии 8 (1) РАВНОВЕСНЫЕ И НЕРАВНОВЕСНЫЕ НОСИТЕЛИ ЗАРЯДА (Шалимова, с.221) Свободные носи­тели заряда, возникающие в резуль­тате термической генерации и находящиеся в тепловом равновесии Одновременно с генерацией сво­бодных носителей заряда идет про­цесс рекомбинации Не могу не вставить здесь еще и Киреева Системы, в которых вероятность нахождения частиц в верхних состояниях больше Для неравновесных систем с нормальным распределением частиц по состояниям используется функция Ферми Прошу обратить внимание на столь любимую студен­тами формулировочку Сначала он ввел два разных уровня Ферми с потолка Неравновесные носители заряда

Подобный материал:

• ). Закон Дальтона: p=knT=k(n, 43.24kb.
• Те исследуется угловое распределение и энергетический спектр электронов при облучении, 18.67kb.
• Кыргызско-турецкий университет «манас» силлабус, 133.57kb.
• Планирование на предприятии, 524.23kb.
• Программа курса введение. Базовые идеи и материалы для построения структур пониженной, 17.33kb.
• Задачи: дать представление о форме различных орбиталей; обобщив полученные знания,, 82.88kb.
• Оценка влияния создания свободных экономических зон на функционирование региональной, 96.83kb.
• I. результаты, представляемые в доклад президента ран, 1441.88kb.
• Нормальный закон распределения наработки до отказа классическое нормальное распределение, 68.45kb.
• Конспект лекций по курсу «Банковское дело» содержание: Тема кредитная система, 1283.92kb.

Введем обозначение

 = 1/_r(n₀ + p₀). (7-17)

Тогда уравнение (7-16) примет вид:

(dn/dt)_r = –(n – n₀)/ = –n₀/, откуда

п = n(0)exp(–t/), (7-19)

где n(0) – избыточная концентрация электронов в момент вы­ключения возбуждающего света.

Таким образом, в случае малого уровня биполярной генерации избыточная концентрация электронов и дырок после прекращения возбуждения уменьшается по экспоненциальному закону и за время  число их в результате рекомбинации убывает в e раз.

Следова­тельно,  представляет собой среднее время существования

избы­точной концентрации электронов и дырок

и называется временем жизни неравновесных носителей заряда.


Для собственного полупро­водника

скорости убывания числа электронов и дырок равны

и ве­личина  определяет время жизни электронно-дырочных пар.

Зна­чение объемного времени жизни неравновесных носителей заряда в зависимости от типа полупроводникового материала и от степени его чистоты может изменяться в очень широких пределах – от 10^–2 до 10^–8 c.

Поскольку величина  достаточна велика, свобод­ные электроны и дырки, диффундируя из приповерхностной об­ласти, где их концентрация повышена, в объем полупроводника, за время жизни успеют пройти большое расстояние. Следовательно, в случае биполярной генерации область генерации носителей заряда и область их рекомбинации пространственно не совпадают.

В случае большого уровня биполярного возбуждения, когда n >> n₀ + p₀, из (7-15) найдем, что

(dn/dt)_r = –_r(n)², (7-20)

то есть скорость рекомбинации носителей заряда зависит от n no квадратичному закону. {И рекомбинация называется линейной.}

Разделяя переменные, запишем:

dn/(n)² = –_rdt, (7-21)

откуда

n = n(0)/[1 + _rn(0)t]. (7-22)

Из равенства (7-22) следует, что при квадратичной рекомбина­ции избыточная концентрация носителей заряда уменьшается по гиперболическому закону.

Если ввести мгновенное время жизни _мгн, то в случае квадра­тичной рекомбинации согласно уравнению (7-20)

(dn/dt)_r = –n/_мгн (7-23)

и

_мгн = 1/_rn, (7-24)

то есть _мгн зависит от концентрации избыточных носителей заряда и в связи с этим является переменной величиной. Однако в каждый момент времени _мгн имеет определенный смысл, являясь мгновенным временем жизни носителей заряда. В силу этого при большом уровне инжекции имеем дело с мгновенным временем жизни, которое согласно уравнению (7-23) равно:

_мгн = –n/(dn/dt). (7-25)


Механизмы рекомбинации


Рассмотрим некоторые наглядные представления о механизме рекомбинации.

По виду передачи энергии рекомбинирующих частиц различают три основных типа рекомбинации.

1. Рекомбинация называется излучательной, или фотонной, если энергия рекомбинирующих частиц выделяется в виде энергии фотона.

2. Если энергия частицы передается решетке (фононам), то реком­бинация называется безызлучательной, или фононной.

3. Одним из видов безызлучательной рекомбинации является ударная ионизация (процессы Оже), когда энергия рекомбинирую­щих частиц передается третьей частице, которая благодаря этому становится «горячей». «Горячая» частица в результате ряда столкно­вений передает свою энергию фононам.

4. Кроме этих трех основных механизмов, энергия рекомбинирую­щих частиц может передаваться электронному газу (плазменная рекомбинация). Если электрон и дырка образуют в качестве про­межуточного состояния экситон, то такая рекомбинация носит назва­ние экситонной.

Фотонная, фононная и рекомбинация Оже могут протекать по-разному в зависимости от механизма перехода электрона из зоны проводимости в валентную зону.

Если частицы рекомбинируют в результате непосредственной встречи электрона и дырки, то такая рекомбинация называется

8 (1) РАВНОВЕСНЫЕ И НЕРАВНОВЕСНЫЕ НОСИТЕЛИ ЗАРЯДА (Шалимова, с.221)

7.1. РАВНОВЕСНЫЕ И НЕРАВНОВЕСНЫЕ НОСИТЕЛИ ЗАРЯДА

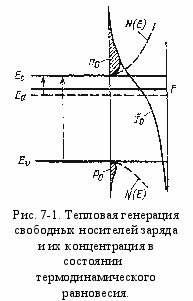
Рассмотрим донорный полупроводник, находящийся в состоя­нии термодинамического равновесия. В результате тепловой ге­нерации электроны с донорной примеси переходят в зону проводи­мости.

При достаточно высоких температурах будет существенным переброс электронов непосредственно из валентной зоны в зону проводи­мости. На рис. 7-1 стрелками пока­заны переходы электронов при теп­ловом возбуждении.

Свободные носи­тели заряда, возникающие в резуль­тате термической генерации и находящиеся в тепловом равновесии, с кристаллической решеткой, назы­ваются равновесными.

На рис.7-1 изображены плотность квантовых состояний N(Е) в зоне проводимости и валентной зоне, функция распределения Ферми–Ди­рака f₀(Е) и концентрация равновес­ных электронов n₀ и дырок p₀, кото­рые занимают состояния вблизи краев соответствующих зон (заштрихован­ные области).

Одновременно с генерацией сво­бодных носителей заряда идет про­цесс рекомбинации: электроны возвращаются в свободные состоя­ния в валентной зоне, в результате чего исчезают свободный элек­трон и свободная дырка. В условиях термодинамического равнове­сия эти процессы полностью взаимно уравновешиваются. Обозна­чим через G₀ число генерируемых, а через R₀ – число рекомбини­рующих электронно-дырочных пар в единице объема кристалла за одну секунду. Вероятность рекомбинации пропорциональна произведению концентраций свободных носителей заряда, поэтому

R₀ = _rn₀p₀. (7-1)

Здесь _к – коэффициент пропорциональности, называемый ко­эффициентом рекомбинации.

Для равновесного со­стояния полупроводника справедливо равенство

G₀ = R₀, (7-2)

которое является выражением принципа детального равновесия.

Помимо тепловой генерации имеются другие механизмы, при­водящие к возникновению свободных носителей заряда. Напри­мер, они могут образоваться при облучении полупроводника све­том, за счет разрыва валентных связей в сильных электрических полях или в результате инжекции с помощью p-п перехода. Во всех этих случаях возникает некоторая концентрация электронов п и дырок p, которая отличается от термодинамически равновесной. Подвижные носители заряда, не находящиеся в термодинамическом равновесии как по концентрации, так и по энергетическому распре­делению, называются неравновесными носителями заряда, а их концентрация п, и p называется неравновесной концентрацией. Из­быток неравновесной концентрации носителей заряда п, и p в по­лупроводнике по сравнению с равновесной п₀, p₀ называется избыточ­ной концентрацией носителей заряда.

При генерации, например при поглощении света, носители за­ряда могут иметь кинетическую энергию, значительно превышаю­щую среднюю тепловую энергию равновесных частиц. В резуль­тате рассеяния на дефектах кристаллической решетки носители заряда довольно быстро передают ей свою избыточную энергию.

Пусть энергия генерированных светом электронов была в зоне про­водимости примерно 1эВ. Рассеиваясь на длинноволновых фононах, они за каждое столкнове­ние будут передавать решетке энер­гию порядка 610^–4 эВ (см. с. 165). Для рассеива­ния своей избы­точной энергии избыточные электроны должны совершить около 1600 столкновений с акустическими фононами. Так как средняя длина свободного пробега электронов порядка 10^–6 см, а их тепло­вая скорость при комнатной температуре составляет приблизи­тельно 10⁷ см/с, при этом среднее время между двумя столкнове­ниями равно   10^–13 с, то уже через 1,610^–10 с избыточные электроны приобретут температуру кристаллической решетки и не будут отличаться от равновесных носителей заряда. Поэтому рас­пределение по энергиям неравновесных и равновесных носителей заряда будет одинаковым. Этот процесс сводится к тому, что не­равновесные электроны, рассеивая свою избыточную энергию, как бы «опускаются» к нижнему краю зоны проводимости, а неравно­весные дырки, рассеивая избыточную энергию, «поднимаются» к верхнему краю валентной зоны. Если при этом концентрация неравновесных носителей заряда мало отличается от равновесной, можно считать, что энергия кристалла практически не изменяется, а значит, не меняется температура кристалла и, следовательно, не меняется концентрация равновесных носителей заряда. В этом слу­чае общее количество электронов и дырок будет равно соответст­венно:

n = n₀ + n;

p = p₀ + p. (7-3)

Стационарную концентрацию неравновесных электронов п можно выразить с помощью формулы, аналогичной (4-40),

n = n₀ + n = _Ec^P_e(E)N(E)dE, (7-4)

где P_e(E) – функция распределения для неравновесных электро­нов, отличная от равновесной функции распределения f₀(E) и стремящаяся к ней при прибли­же­нии неравновесной системы к со­стоянию термодинамического равновесия. Это выражение можно представить в виде, аналогичном соотношению (4-42), введя ква­зиуровень Ферми для электронов в неравновесном со­стоянии F_n так, чтобы выполнялось условие

n = N_cF_1/2(_n) (7-5)

где

_n = (F_n – E_c)/kT (7-6)

есть приведенный квазиуровень Ферми для электронов.

Концентрацию неравновесных электронов в невырожденном по­лупроводнике с учетом равенств (4-65), (4-66) и (4-69) можно пред­ставить в виде

n = N_cexp(_n) = n₀exp(_n – ) = n₀exp(_n – _i). (7-7)

Аналогично концентрацию неравновесных дырок можно выра­зить следующим образом:

p = p₀ + p = _–^EvP_h(E)N(E)dE, (7-8)

где

_p = (F_p – E_v)/kT (7-9)

есть приведенный квазиуровень Ферми для дырок.

При отсутствии вырождения, учитывая формулы (4-67) и (4-69), можно написать:

p = N_vexp(–_p – _i) = p₀exp( – _p) = n_iexp(_i – _p). (7-10)

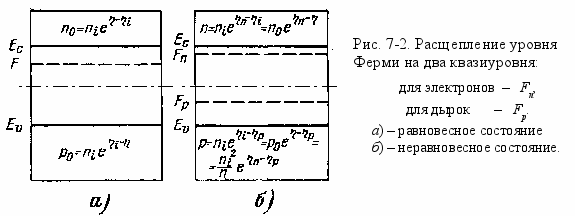
Таким образом, в неравновесном состоянии уровень Ферми как бы расщепляется на два квазиуровня – для электронов F_n и для дырок F_p (рис. 7-2).

Произведение концентраций электронов и дырок для неравно­весного состояния отличается теперь от его значения для равновес­ного состояния:

n
p = n₀p₀exp(_n – _p) = n_i²(_n – _p). (7-11)

Расстояние между приведенными уровнями Ферми (F_n – F_p) характеризует отклонение системы от состояния термодинамического равновесия:

np/n₀p₀ = np/n_i² = exp(_n – _p) (7-12)

Это соотношение выражает связь между концентрациями электронов и дырок неравновесном состоянии. При этом, чем сильнее различаются квазиуровни Ферми электронов и дырок, тем сильнее отличается произведение концентраций неравновесных носителей заряда от произведения равновесных концентраций.

________________________________________________________________

Не могу не вставить здесь еще и Киреева.

Раздел: § 65. МЕХАНИЗМЫ РЕКОМБИНАЦИИ. ЛИНЕЙНАЯ РЕКОМБИНАЦИЯ

Неравновесное состояние свободных носителей заряда может быть описано некоторой функцией распределения f(r,k,t), вид которой был найден в четвертой главе для случая, когда отклонение от равно­весного состояния вызывается полями E и B, градиентами хими­ческого потенциала F (энергии Ферми) и температуры.

Неравновес­ная часть функции распределения f⁽¹⁾ описывает перераспределе­ние частиц по состояниям в зоне Бриллюэна при сохранении числа частиц. При втором типе неравновесных состояний, когда концентра­ция частиц меняется, характер изменения функции распределения должен быть другим. Предположим, что для описания неравновес­ных состояний можно воспользоваться функцией Ферми-Ди­рака с другими значениями входящих в нее параметров.

Системы, в которых вероятность нахождения частиц в верхних состояниях больше, чем в нижних, называют системами с инверсной населенностью. Для их описания необходимо считать температуру величиной отрицательной. Системы с отрицательными температу­рами используются для создания квантовых генераторов и усили­телей.

Для неравновесных систем с нормальным распределением частиц по состояниям используется функция Ферми–Дирака (или функция Больцмана), в которой энергия Ферми F заменяется некоторой вели­чиной F*, называемой квазиуровнем Ферми. Квазиуровень Ферми F* можно ввести как величину, определяющую нормальное распределение частиц по состояниям в системах с неравновесной концентрацией носителей заряда. Величину F* можно определить из условия нор­мировки аналогично тому, как это было проделано для уровня Ферми:

n = (2N_c/^1/2)Ф_1/2(*), * = (F* – E_c)/kT; (65.1)

n = (2N_v/^1/2)Ф_1/2(*), * = (E_v – F*)/kT; (65.2)

Для невырожденных полупроводников можем записать


n = N_cexp(F_n* – Ec); p = N_vexp(E_v – F_p*) (65.3)

и

np = N_cN_vexp(–E₀/kT)exp[(F_n* – F_p*)/kT] = n_i²exp[(F_n* – F_p*)/kT]. (65.4)

Как видно из (65.4), квазиуровни Ферми электронов и дырок в неравновесных системах различны^). Чем сильнее различаются ква­зиуровни Ферми электронов и дырок, тем сильнее отличается произ­ведение неравновесных концентраций от произведения равновесных концентраций.


______________

^) Прошу обратить внимание на столь любимую студен­тами формулировочку:

«Как видно из формулы (в данном случае из 65.4) квазиуровни Ферми электронов и дырок в неравновес­ных системах различны».

Заметили, что это стало известно именно из формулы?!

Сначала он ввел два разных уровня Ферми с потолка «из условия нормировки», а именно: F_n* – уровень Ферми для электронов и F_p* – уровень Ферми для дырок, вставил это в формулы безо всякого объяснения и обоснования, после чего из этих же формул делает мудрый вывод, что уровни Ферми различны.


Здорово, правда?

Шалимова, правда, тоже себя не утруждает объяснением, почему уровни различны. Но она и не говорит, что разницу выудила “из формул”. В.Г.


НЕРАВНОВЕСНЫЕ НОСИТЕЛИ ЗАРЯДА

Неравновесные носители заряда (Бонч-Бруевич, с.244)


… При наличии внешних воздействий на полупроводник к тепловым перехо­дам v₁₂ добавляются переходы v₁₂' нетеп­ловой природы, и при этом частота обрат­ных переходов v₂₁ тоже изменяется. Со­стояние полупроводника в таких усло­виях мы будем называть термодинами­чески неравновесным. При этом принцип детального равновесия, вообще говоря, уже не выполняется.

При нарушении термодинамического равновесия концентрации электронов и дырок в зонах n и p изменяются по сравнению с их равновесными значениями n₀ и p₀, то есть в зонах появляются неравновесные носители заряда с концентрациями

n²⁾ = n – n₀ и p = p – p₀.

При этом изменяются и концентрации связанных носителей n_t и p_t.

Сказанное справедливо, конечно, и для металлов. Однако кон­центрация электронов в металлах гораздо больше, чем в полупро­водниках, и ее относительное изменение обычно ничтожно мало.

Отметим, что уже в гл. VI мы имели дело, по существу, с иерав­новесными состояниями, так как наличие тока нарушает термоди­намическое равновесие (ср. §VI.3). Однако там можно было счи­тать, что по отношению к концентрации носителей заряда равнове­сие сохраняется. Это значит, что для данного полупроводника при заданной температуре установившаяся концентрация электронов определяется только значением электростатического потенциала (ср., например, §VI.12). Теперь мы рассмотрим явления, в которых нарушается равновесие и по концентрациям. Именно такие состоя­ния мы будем называть в дальнейшем неравновесными.


§ 2. Время жизни неравновесных носителей заряда

В настоящей главе мы будем рассматривать поведение неравиовес­ных носителей заряда только в объеме полупроводника, отвлекаясь от возможного влияния его поверхности. Это можно сделать, если отношение поверхности к объему образца достаточно мало (строго говоря, для бесконечно протяженного полупроводника). Однако основные понятия и соотношения, вводимые в настоящей главе. сохраняются и в тех случаях, когда процессами генерации и реком­бинации на самой поверхности пренебрегать нельзя. Влияние по­верхности на неравновесные состояния будет рассмотрено дополни­тельно в гл.X, где будут выяснены и условия, при которых этим влиянием можно пренебречь.

Положим, что под влиянием внешнего воздействия в каждой единице объема полупроводника в единицу времени возникает g_n электронов проводимости и, соответственно, g_p дырок в валентной зоне. Темпы генерации g_n и g_p будем считать сначала одинаковыми по всему объему, хотя и не обязательно равными друг другу. Пусть, далее, R_n есть темп обратного процесса исчезновения свободных электродов вследствие процессов рекомбинации с дырками (свобод­ными и связанными на локальных уровнях энергии) и, соответст­венно, R_p — темп рекомбинации свободных дырок. Если в полу­проводнике нет электрического тока, то изменение во времени неравновеспых концентраций электронов и дырок в зонах определя­ется уравнениями

dn/dt = g_n — R_n, dp/dt = g_p — R_p (2.1)

Подчеркнем, что g_n и g_p обозначают генерацию, обусловленную только внешними воздействиями, и не включают переходы, вызван­ные тепловвым движением. Последние мы учитываем в величинах R_n и R_p, которые поэтому представляют результирующие темпы рекомбинации, то есть разности между темпом захвата носителей из соответствующей зоны и темпом обратной тепловой генерацией носи­телей в зону:

R_n = r_n — g_nT, R_p = r_p — gp_nT. (2.2)

Для количественного описания кинетики неравновесных элек­тронных процессов широко применяют понятия среднего времени жизни неравновесных электронов в зоне проводимости _n и. соот­ветственно, дырок в валентной зоне _p, которые определяются формулами

R_n = (n — n₀)/_n, R_n = (p —p₀)/_p. (2.3)

Или иначе: 1/_n есть вероятность исчезновения одного избыточного электрона из зоны проводимости в единицу времени вследствие рекомбинации (со свободными и связанными дырками). Аналогично, 1/_p есть вероятность рекомбинации одной избыточной дырки, тоже за единицу времени.

Так как _n и _p в формулах (2.2) по физическому смыслу не могут иметь слагаемых, не зависящих от n и, соответственно, p, то из


сравнения формул (2.2) и (2.3) следует, что

gn = n0/r g=.p0/ (2.4)

Следовательно, времена Тд и Тр определяют не только темп суммарной рекомбинации, но и темп тепловой генерации электронов и дырок. Пользуясь понятиями времен жизни, уравнения кинетики (2.2) для однородного образца без тока можно записать в виде

dn 6п dbp 6р

•dT-en- w-gp- <²-⁵)

Стационарные концентрации неравновесных носителей заряда. устанавливающиеся после длительного воздействия внешней гене­рации, равны

(6=g, (6p)s-gp. (2.6)

Величины Хп и Гр зависят от физических особенностей элементар­ных актов рекомбинации электронов и дырок. При этом Тл и т, вообще говоря, могут сами зависеть от неравновесных концентраций 6д и 6р, а также от температуры. Поэтому Тд и Гр не являются харак­теристиками данного полупроводника, но зависят еще от условий опыта. Эти вопросы будут подробнее рассмотрены в гл.IX (см. также § XVI 1.9). Сейчас же мы будем считать т и Гр заданными феноменологическими величинами, определяющими кинетику элек­тронных процессов.

В простейшем случае, когда Тд и т не зависят от п и р, интегри­рование уравнений (2.5) дает

6п = gntn — С ехр (— thn)

и такое же выражение для концентрации неравновесных дырок бр. Здесь С—постоянная интегрирования, определяемая начальными условиями. Так, если вначале полупроводник находился в термо­динамическом равновесии и затем в момент времени / == 0 было включено внешнее воздействие, мы имеем / ==- 0, бп = 0. Это дает

С - gnn - (6п)„ 6п = (6п), [1 » ехр (~ //т,)]. (2.7а)

Если в некоторый момент времени t == /i генерация выключается, то для / /I, gn == 0, а начальное условие есть / =- /i, 6п = (6/?)i. Тогда

С — (6n)i ехр ^/1, 6п - (6n)i ехр (- (/ - )/т„). (2.76)

-rt

При постоянном Тд установление избыточной концентрации элек­тронов и ее исчезновение описываются экспоненциальным законом, а среднее время жизни т„ есть время, в течение которого концентра­ция неравновесных электронов изменяется в e раз. То же справедли­во и для неравновесных дырок.


В общем случае Хп и Гр, изменяющихся вместе с п и р, соотноше­ния (2.3) определяют мгновенное времена жизни. Величины 1/т/г и 1/Тр в этом случае дают вероятности рекомбинации одной частицы в единицу времени при данных значениях п и /?, а Тд и Гр определяют времена, за которые неравновесные концентрации электронов или, соответственно, дырок изменились бы в e раз, если бы вероятность их рекомбинации сохранялась постоянной и равной данному мгно­венному значению.


7 (1) Подвижность носителей (T)