Варшавский В. И., Поспелов Д. А

Вид материала

Документы

Содержание Вместо предисловия Просто ли существовать в сложном мире? Омар Хайям Рii характеризуют вероятность того, что на следую­щем шаге автомат будет взаимодействовать с той же средой ei М* — время жизни автомата с начальным сос­тоянием j при оптимальном переключении им сред, d(i) — Станислав Ежи. Лец С. Маршака) Г л а в а 4 КОГДА "ВСЕ ПО СПРАВЕДЛИВОСТИ" N нуждающихся в квартирах, и имеется т 1—E сохранять их неизмен­ными с вероятностью E So автомата. Инициирующий сигнал поступает на край­ний автомат цепи А Ai поступает входной сигнал Xi Во справа на младший разряд множителя. Этот сигнал как бы 170 считывает значение разряда. Появление после этого состояния D Г л а в а 6 ДИАЛЕКТИКА ПРОСТОГО И СЛОЖНОГО В и Г. Для удобства будем обозначать такой автомат как А Литература и комментарий Предметный указатель Глава 2. Просто ли существовать в сложном мире? ... 26

Подобный материал:

• Герберт Александер Саймон Исследователи ии: Лотфи Заде Исследователи ии: А. А ляпунов,, 9.34kb.
• «Как привлечь средства государственных институтов развития» Варшавский Владислав Римович, 48.54kb.
• Аннотация к научно-образовательному материалу, 114.81kb.
• 141. Поспелов В. И., Стальнов В. С. Содружественная аккомодация глаз при дисбинокулярной, 167.36kb.
• Тезисы докладов участников III международного конгресса «Россия и Польша: память империй, 1372.37kb.
• Д. А. Поспелов, Г. С. Осипов, 487.33kb.
• Варшавский А. С. Следы на дне, 1828.32kb.
• Рабочая программа учебной дисциплины Для направления 080100. 62 «Экономика» (программа, 562.39kb.
• Диспут с Пирром: прп. Максим Исповедник и христологические споры VII столетия / Отв, 73.89kb.
• Программа дисциплины: Имитационные модели для направления Прикладная математика и информатика, 120.53kb.

Варшавский В. И., Поспелов Д. А.

Оркестр играет без дирижера: размышления об эволюции некоторых технических систем и управлении ими.—М.: Наука. Главная редакция физико-математической литературы, 1984.— 208 с., 50 илл.


Мир, создаваемый человеком в технических системах, во многом похож на тот, который окружает человека в природе. И в искусст­венном мире техники могут происходить процессы, подобные эволю­ции живых организмов. Возникают колонии и сообщества техниче­ских систем, формируются «сверхорганизмы» типа муравейника, возникают «коллективы», живущие по своим законам. Авторы книги анализируют эти аналогии и рассматривают принципы построения управления в таких технических системах, которые во многом от­личаются от привычных схем управления. Для чтения книги не требуется никакой специальной подготовки, хотя она обращена не только к так называемому широкому читателю, но и к специали­стам, работающим в области управления и кибернетики.


Издательство «Ника» Главная редакция

физико-математической Литературы, 1981


ВМЕСТО ПРЕДИСЛОВИЯ


13 февраля 1922 года в Москве состоялось пер" вое публичное выступление Персимфанса — Первого симфонического ансамбля Моссовета. Это выступле­ние стало настоящей сенсацией для всех профессио­налов и любителей музыки.

Дело в том, что Персимфанс исполнял музыку без дирижера. И не какие-нибудь легкие для коллектив­ного исполнения сочинения. В его первой программе прозвучали такие серьезные музыкальные вещи, как Третья (Героическая) симфония Бетховена или кон­церт для скрипки с оркестром того же автора. И звучали они настолько слаженно и артистично, что профессионалы уходили после концерта в пол­ном недоумении. Им казалось, что в игре Персим­фанса есть какой-то трюк, фокус, кто-то скрытно дирижирует оркестром, создает то неповторимое исполнение, которое может обеспечить лишь воля дирижера. Ибо лишь дирижер способен дать свою, глубоко индивидуальную интерпретацию музыкаль­ного произведения, навязать динамику исполнения, синхронизировать партии различных инструментов, заставить огромный оркестр звучать слаженно. Имен­но поэтому обычно музыканты сидят на сцене так, чтобы видеть дирижера и следовать его указаниям.

А музыканты Персимфанса сидели совсем иначе. Струнные сидели, образуя полный круг (частично спиной к зрителям!), а духовые располагались в середине этого круга. Каждый музыкант видел каждого, ибо в Персимфаисе каждый слушал каж­дого и всех, а все слушали каждого. Не было ника­кого трюка. Взаимодействуя непосредственно друг с другом, прекрасные музыканты, входившие в Перспмфанс, легко обходились без дирижера.

Десять лет продолжались с неослабевающим успехом выступления Персимфанса, и все это время загадка этого оркестра интересовала и широкую публику, и специалистов. В рамках общей цели — достижения артистичного исполнения того или иного

3


произведения, каждый музыкант реализовал наи­лучшим образом свою локальную цель, демонстрируя в полной мере свои профессиональные возможности. (Другим примером, возможно более близким некото­рым читателям, может служить джазовый ансамбль, играющий в стиле диксиленд.) Таким образом, вместо централизованного управления, реализуемого дирижером, в Персимфансе восторжествовал децен­трализованный способ управления. Этот способ реализовался за счет коллективного взаимодействия музыкантов, которое «порождало» процесс управле­ния. Но как это происходило, оставалось непонятным, не укладывалось в четкие и формальные правила.

Подобная ситуация, когда сложные процессы развиваются не за счет централизованных воздейст­вий, а за счет локальных взаимодействий их элемен­тов, широко распространена в природе и в челове­ческом обществе. Она встречается гораздо чаще, чем это может показаться на первый взгляд. А, значит, вопрос о том, как рождается децентрализованное управление в результате коллективного взаимодей­ствия элементов—куда глубже того, который возник у тех, кто стремился понять загадку Персимфанса. Ответ на него — одна из целей этой книги.

Авторы ее поставили перед собой задачу рассказать на популярном уровне о проблемах управления в сложных системах, которые в теории управления принято называть большими. В подобных системах часто приходится переходить от централизованного управления к децентрализованному. Это представляет собой как бы плату за сложность, присущую боль­шим системам. Централизованное управление в них, как правило, неэффективно, а в ряде случаев просто невозможно. Но откуда берутся столь сложные си­стемы? Не есть ли категория больших систем паду' манной? Как мы постарались показать в книге, мир больших систем, окружающих человека, все время обогащается. Рост сложности искусственных систем, создаваемых человеком, происходит постоянно. Идет эволюционное развитие созданных ранее искусствен­ных систем, в какой-то степени напоминающее эво­люцию в мире живых организмов. Децентрализован­ное управление—закономерное порождение этой эволюции. И наша задача — убедить читателей в справедливости этих утверждений.


Глава 2 ПРОСТО ЛИ СУЩЕСТВОВАТЬ В СЛОЖНОМ МИРЕ?


«Подражанье, повторенье — мира этого дела.

Если бы не повторенье, жизнь бы праздником была, —

Награждались бы старанья, исполнялись бы желанья,

А возмездия угроза бесполезная спала».

Омар Хайям


§ 2.1. Парадоксы целесообразности

Лиса вернулась с богатой добычей. Часть ее на­сытила лисий выводок, а оставшуюся пищу лиса прячет «на черный день». Тщательно роет яму, кла­дет в нее мясо и засыпает его землей. Наблюдая за ее поведением, можно прийти к выводу, что цель действий лисицы порождена ее «интеллектом». Столь целесообразно и «разумно» ее поведение.

Но судьба оказалась для нашей героини по очень счастливой. Она попала в западню и стала жительницей зоопарка. Теперь ей уже не прихо­дится тратить силы на добывание пищи. Ее кормят служители. Но что делать лисе, когда пищи избыток? Конечно, спрятать! И лиса скребет когтями бетонный пол вольера, а через некоторое время, когда «яма» готова, «прячет» в нее мясо. И после этого перестает обращать внимание на остаток трапезы, который, конечно, так и остается лежать на полу вольера. Лиса просто игнорирует его, не видит «зарытое» мясо. То, что в привычной для животного среде вы­глядело целесообразно, в условиях другой реальности становится лишенным каких-либо черт разумности.

Такие узко специализированные действия, тесно связанные с типовой ситуацией в окружающем мире, принято называть рефлексами. Чем проще организо­ван организм, тем жестче схема рефлекса. Тем неле­пее выглядит их поведение в изменившейся среде. Разных видов рефлексов существует немало и клас­сификация их довольно неустойчива. Для нас важно лишь то, что существуют рефлексы, которые помогают

26

живому организму приспосабливаться к условиям той среды, в которой он обитает.

Р

ассмотрим два небольших примера. Зоопсихо­логи очень любят использовать для наблюдения за поведением живых организмов и за изменением это­го поведения в условиях той или иной среды спе­циально сконструированные лабиринты. Площадки и коридоры лабиринтов снабжаются всевозможными


приятными и неприятными для живущего в нем раз­дражителями. А различные размещения этих раз­дражителей позволяют экспериментаторам создавать по своему желанию ту или иную «географию» среды обитания.

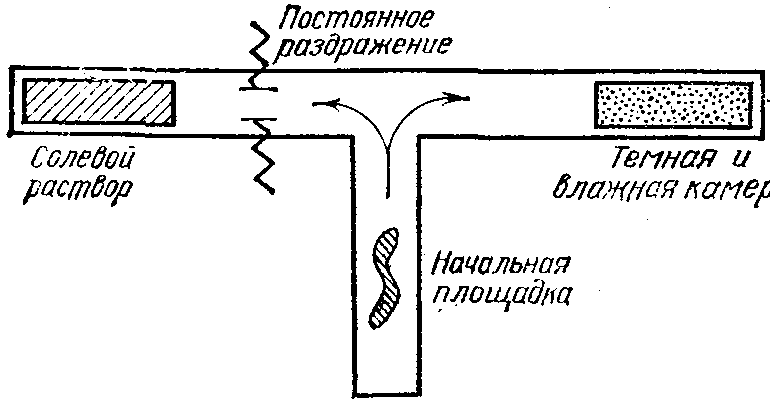
Простейшие лабиринты — Т-образные. На рис. 2.1 показано два таких лабиринта. Рассмотрим сначала верхний. Его использовал для своих опытов с обыч­ными дождевыми червями американец Йеркс. В на­чале опыта черви помещались на площадку в осно­вании буквы Т. Эту площадку ярко освещали, и червь начинал движение, стремясь найти более комфортабельное место. Там, где коридор имел раз-

27


ветвление, червь мог сделать выбор из двух альтер­натив: поворачивать влево или поворачивать вправо. Конечно, червь «не мог знать», что левый коридор сулит ему одни неприятности. По дороге налево включено электрическое поле, а камера в конце коридора представляет собой ванночку с раздражаю­щим червя солевым раствором. Зато правый коридор приводил червя в затемненную и влажную камеру, где он чувствовал себя превосходно.

В' процессе эксперимента червь многократно пре­одолевал лабиринт и «принимал решение» о выборе коридора при разветвлении. И постепенно обучался поворачивать только в правый коридор. Другими словами, не имея никакой первоначальной информа­ции об особенностях среды обитания, червь в про­цессе взаимодействия с окружающим миром выра­батывал целесообразный способ поведения в нем.

Изменение среды экспериментатором (например, замена раздражителей левого коридора на благо­приятные условия правого и перенесение этих раздра­жителей в правый коридор) делало поведение обу­ченного червя нецелесообразным. Казалось бы, что червь должен был бы до конца своего существования быть в полном разладе с окружающей его средой. Но через некоторое число безуспешных попыток найти в правом коридоре уютную камеру для отдыха червь впервые поворачивал в левый коридор. Шло переучивание. И снова наступала пора полной адап­тации червя к изменившемуся миру.

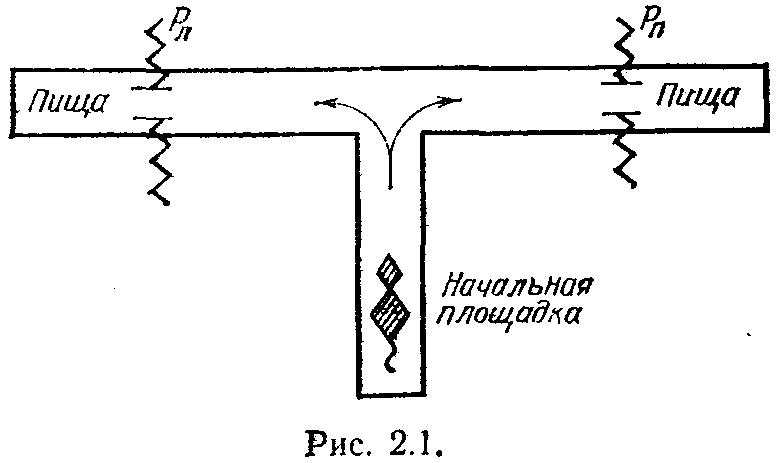
Рассмотрим теперь нижний лабиринт, показанный на рис. 2.1. Его использовал другой зоопсихолог— Торндайк для опытов с крысами. При разветвлении коридора голодная крыса, привлекаемая запахом приманки, должна сделать альтернативный выбор между левым и правым коридорами. Но в каждом из них крысу ждут неприятные ощущения от раздра­жения электрическим током. Эти раздражения про­исходят с фиксированными вероятностями Рп и Pл, которые не изменяются в одной серии опытов. Цель эксперимента — определить, сможет ли крыса в процессе обучения научиться выбирать только тот коридор, ведущий к пище, в котором вероятность электрического раздражения меньше.

Опыты Торндайка повторяли неоднократно. В экспериментах принимали участие не только кры-

28

сы, но и другие животные. Формы лабиринтов изме­няли. Но основной качественный результат во всех экспериментах оставался неизменным. После более или менее длительного периода обучения наступал момент, когда животное правильно оценивало раз­ницу в значениях Ру и Рл (в случае Т-образного лабиринта) и принимало целесообразное решение по выбору маршрута движения к пище. При незна­чительной разнице в значениях вероятностей болевых раздражении выбор пути движения происходил без заметных предпочтений.

Казалось бы, что математики должны были бы обратить на эти интересные факты свое внимание. Но этого не произошло. Эпоха моделей и открытий на стыке наук еще не наступила, науки еще сильно разобщены, у представителей каждой из них свой «внутрицеховой» язык, непонятный для непосвящен­ных. Интерес к результатам в соседних областях знаний минимален. Идет глубокий анализ явлений в отдельных областях, а время синтеза и интеграции знаний еще отделено от времени опытов Торндайка десятилетиями. Альянс между математикой и зоо­психологией в те далекие годы, предшествующие первой мировой войне, не состоялся. Математики не заметили опытов Торндайка, а психологи были очень и очень далеки от овладения языком мате­матики.

И лишь через 50 лет наступило время посмотреть па поведение червей и крыс с иной точки зрения.

§ 2.2. «Маленькая зверушка»

Моделирование и объяснение эффекта Йеркса и Торндайка были получены в цикле исследований по моделированию простейших форм поведения, выпол­ненных в 60-х годах нашего века оригинальным и глубоким советским ученым, оказавшим заметное влияние на все развитие работ в области моделиро­вания поведения, Михаилом Львовичем Цетлиным. Он был одповременно и изобретательным инженером, и великолепным математиком. Активно и вовсе не дилетантски интересовался медициной и биологией. Талант инженера, превосходная математическая интуиция и способность к точной, но одновременно весьма образной интерпретации фактов самых раз-

29

личных областей науки позволили ему объединить усилия специалистов в области математики, биологии, психологии, технических наук. Этот «незримый кол­ледж» сложился в своеобразное научное направление, подобного которому в то время, пожалуй, не было нигде в мире. В рамках этого научного коллектива были решены многие важные научные и прикладные проблемы (например, впервые в мире создан био­управляемый протез). Но нас интересует лишь одно направление в его работе. Направление, которое вылилось со временем в новую научную теорию — теорию коллективного поведения и управления.

В
основе этой теории лежит гипотеза простоты, высказанная М. Л. Цетлиным. Суть ее сводится к тому, что любое достаточно сложное поведение слага­ется из совокупности про­стых поведенческих актов. Их совместная реализация и простейшее взаимодей­ствие приводят в резуль­тате к весьма сложным поведенческим процессам. Отсюда возникла идея о том, что совместное функци­онирование простых «ма­леньких зверушек» в слож­ной среде способно обеспечить устойчивое существо­вание всего коллектива, который можно рассмат­ривать как некий «сверхорганизм». Клетки челове­ческого тела, пчелы улья или муравьи муравей­ника должны вызвать у читателя нужную ассо­циацию.

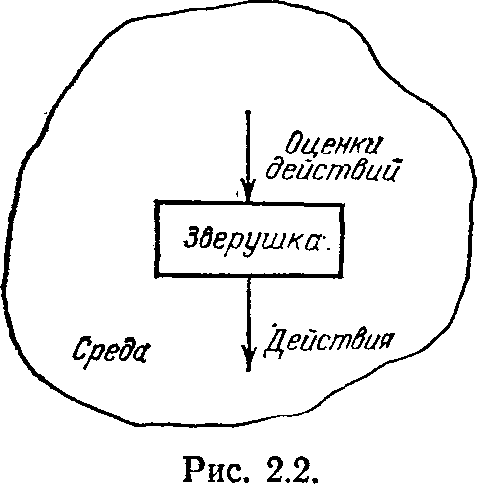
Вернемся к схеме опыта Торндайка. На рис. 2.2 показана некоторая интерпретация этой схемы. Ма­ленькая зверушка воспринимает из окружающей среды сигналы, которые являются оценками действий, совершенных ею перед этим. Эти оценки будут нами рассматриваться как двоичные: поощрение за вы­полненное действие (нештраф) и наказание за него (штраф). Зверушка может выбирать свои действия из некоторого заданного конечного набора D==[di, ds, ..., dn]. Значения оценок действия (будем их обозначать 1 и 0) формируются средой. Одна среда

30

отличается от другой тем, как вырабатываются оцен­ки. Рассмотрим один важный частный случай, когда среда формирует эти оценки следующим образом. Если зверушка делает в некоторый момент действие di, то с вероятностью Pi среда выдает оценку «на­казание» (штраф) и с вероятностью 1—Pi —оценку «поощрение» (нештраф). Если с течением времени значения Pi остаются неизменными, то такая среда называется стационарной. Для полного определения стационарной среды достаточно задать вектор E=(P1,P2,...,Pn).

Вернемся к опыту с крысой, описанному выше. В нем мы имеем дело со стационарной средой вида Е=(Рп,Рл), компоненты которой характеризуют вероятности наказаний (болевых раздражений) при выборе крысой правого или левого коридоров в Т-образном лабиринте. Эти выборы характеризуют множество действий крысы.

М. Л. Цетлин поставил перед собой вопрос: «Сколь сложным должна быть зверушка, которая подобно крысе в опытах Торндайка могла бы адаптировать свое поведение к стационарной среде так, чтобы всегда вести себя наиболее целесообразным образом?» Но прежде чем дать ответ на подобный вопрос, сле­дует уточнить само понятие целесообразности по­ведения.

Заменим нашу зверушку механизмом случайного равновероятного выбора действий. На каждом шаге своего функционирования этот механизм, никак не учитывая приходящих на его вход сигналов штраф — нештраф, с одинаковой вероятностью, равной 1/п, выбирает любое из доступных ему действий. В опы­тах с крысами это соответствовало бы следующей ситуации. Перед началом левого и правого коридоров имеются запирающиеся дверцы. Когда крыса под­бегает к развилке, то всегда оказывается открытой лишь одна из них. Открывание их происходит равно­вероятно. Для этого экспериментатор может, например, подбрасывать монету и на основании вы­падения ее той или иной стороной открывать соот­ветствующую дверцу. В таких условиях крыса, ко­нечно, лишена возможности принимать какое-либо решение о выборе маршрута движения. Это решение «принимает» за нее механизм случайного равновероят­ного выбора.

81

П
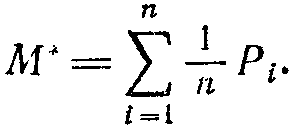
ри бесконечном повторении опыта со зверушкой, устроенной как механизм равновероятного выбора действий, будет накоплен некоторый суммарный штраф. Его величина определяется как математиче­ское ожидание штрафа по формуле, хорошо извест­ной в теории вероятностей:

Значение М* позволяет интерпретировать понятно целесоорбазного поведения следующим образом. Будем говорить, что зверушка ведет себя целесооб­разно, если накопленный ею суммарный штраф меньше, чем в случае механизма равновероятного выбора действий. А нецелесообразным будем считать такое поведение, при котором этот суммарны» штраф оказывается больше М*.

Пусть, например, в Т-образном лабиринте Рп=0,9, а Рл = 0,4. Если бы крыса заранее знала эти вероят­ности, то она, конечно, всегда бы предпочитала бе­жать в левый коридор. Суть опытов Торнданка а том, что именно это предпочтение и сформируется у крысы после некоторого опыта предварительного обучения. Если при наших значениях вероятностей штрафов за действия крысу поставить в условия рав­новероятного выбора (ввести открывающиеся равно­вероятно дверцы), то суммарное значение штрафа для нее будет равно М == 0,5*0,9 + 0,5*0,4 == 0,65. Поведение крысы будет целесообразным, если сум­марный штраф, накопленный ею, будет меньше 0,65. А наилучшим ее поведением будет то, при кото­ром этот штраф достигнет своего минимума (при вы­боре только левого коридора). В этом случае М=0*0,9+1*0,4=0,4.

Поставим перед собой следующую задачу: можно ли построить техническое устройство, которое вело бы себя аналогично нашей зверушке, обеспечивая целесообразное поведение в любой априорно неиз­вестной стационарной среде? И одним из удивитель­ных результатов теории коллективного поведения явилось создание конструкции ряда технических устройств, способных к этому.


32

§ 2.3. Линейная тактика — залог успеха

П
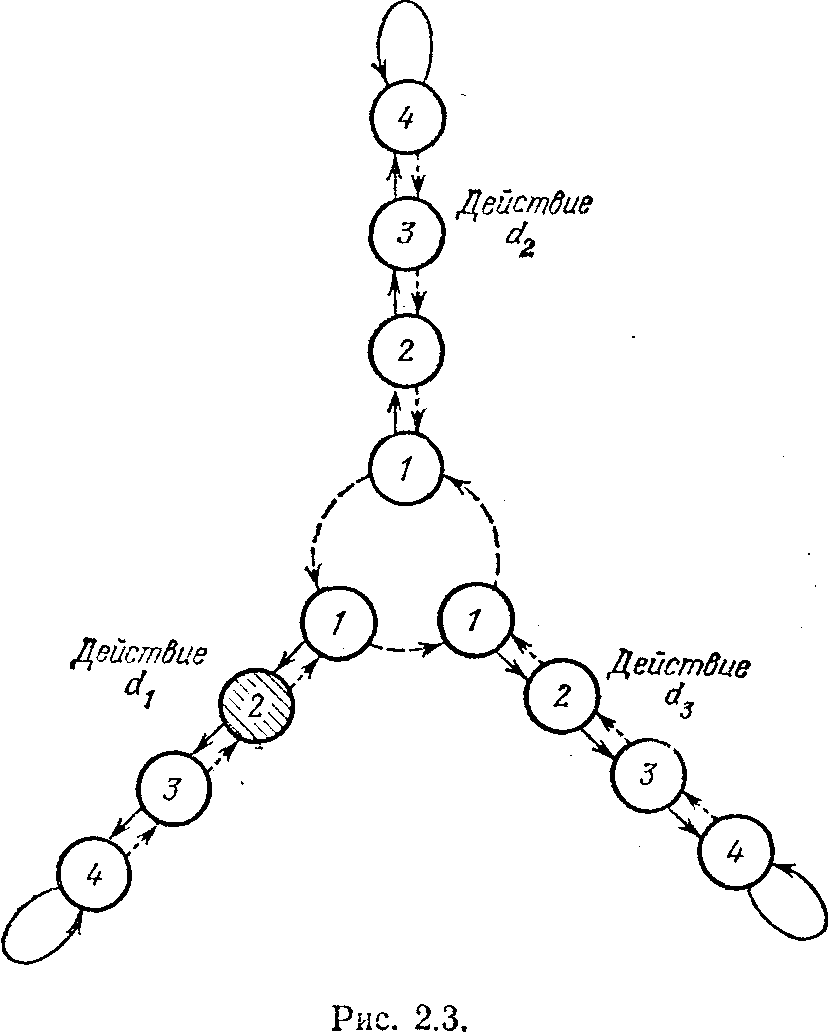
ервой конструкцией такого типа был автомат с линейной тактикой, предложенный М. Л. Цетлиным. На рис. 2.3 показан принцип функционирования по­добного устройства. Число лепестков «ромашки»


равно числу действий, доступных автомату. На ри­сунке для простоты показан случай, когда число таких действий равно трем. В каждом лепестке вы­делено четыре устойчивых состояния, в которых мо­жет находиться автомат. В любом из состояний, образующих лепесток ромашки, устройство выдает в среду сигнал действия, приписанного этому лепестку. Смена состояний происходит с учетом сигналов оце­нок за действия, поступающих от внешней среды. Как уже говорилось, эти сигналы двоичные. При поступлении сигнала нештраф наступает смена со­стояний, показанная на рис. 2.3 сплошными стрелка­ми. Автомат как бы переходит к внешнему краю ле-

83


пестка, а когда достигает последнего состояния в лепестке, то остается в нем. Если же на вход авто­мата приходит сигнал штраф, то состояния сменяют­ся в соответствии с пунктирными стрелками на рисунке. Автомат идет в глубь лепестка, в какой-то момент под влиянием сигнала штраф переходит «а другой лепесток ромашки и происходит смена дей­ствий автомата. Смена лепестков, как видно из рисунка, происходит поочередно.

Поясним теперь принцип работы устройства по­добного типа. Пусть оно взаимодействует со стаци­онарной средой, характеризуемой вектором вида Е = (0,9, 0,0001, 0,8). И пусть в начальный момент наше устройство находилось в состоянии, показанном на рис. 2.3 штриховкой. Понаблюдаем за его функ­ционированием. Находясь в заштрихованном состоя­нии, устройство выполнит действие d1. За это дей­ствие среда с вероятностью 0,9 оштрафует нашу зверушку и лишь с вероятностью 0,1 поощрит ее. Тогда устройство с вероятностью 0,9 перейдет из заштрихованного состояния в состояние 1 в том же лепестке, а с вероятностью 0,1 — в состояние 3 в том же лепестке. В любом случае оно снова произведет в среде действие d1. И опять неумолимая среда с вероятностью 0,9 выдаст сигнал штраф и лишь с ве­роятностью 0,1 поощрит устройство. Как следует из формул теории вероятностей для независимых собы­тий (а выработка сигналов средой на каждом шаге происходит независимо от других шагов), вероят­ность получения от среды двух сигналов штрафа подряд за действие d1 есть 0,9*0,9 == 0,81, вероят­ность получения двух поощрений подряд равна 0,1*0,1 = 0,01, а вероятность получить один штраф и одно поощрение — 0,9*0,1+0,1*0,9=0,18. Это означает, что после двух тактов взаимодействия со средой наше устройство с вероятностью 0,01 ока­жется в состоянии 4 группы состояний, соответствую­щих действию d1, с вероятностью 0,18 останется в заштрихованном состоянии и, наконец, с вероят­ностью 0,81 перейдет в состояние 1 той группы, ко­торой соответствует действие d3. С ростом числа взаимодействий качественная картина не изменится. Вероятность покинуть группу состояний, в которой совершается действие d1, неуклонно возрастает, а вероятность остаться в ней — падает,

84

Что произойдет, когда устройство перейдет в состояние 1 того лепестка, который соответствует действию d3? После формирования этого действия среда с вероятностью 0,8 оштрафует устройство, и оно перейдет в состояние 1 того лепестка, которому соответствует действие d2. С вероятностью же 0,2 будет получен сигнал поощрения, который заставит наше устройство перейти в состояние 2 лепестка, соотносимого с действием d3. Но, как и в предшест­вующем случае, вероятность остаться в состояниях этого лепестка будет убывать с ростом числа взаимо­действий, и автомат в конце-концов покинет и этот лепесток, перейдя в группу состояний, соответствую­щих действию d2. Здесь наблюдается иная картина. Поскольку величина вероятности штрафа за действие d2 весьма мала, то с большой вероятностью автомат заберется в последнее состояние лепестка и почти не будет покидать его. Вероятность уйти на другие лепестки ничтожно мала. По порядку величин она равна 10*E-15. А это значит, что после некоторого периода обучения автомат, имитирующий поведение зверушки, будет вести себя почти самым наилучшим образом. «Почти» связано с тем, что существует не­нулевая, хотя и очень малая, вероятность ухода авто­мата из состояния, соответствующего действию d2. Тогда после очередного периода блуждания по ле­песткам действий d1 и d3 автомат вновь вернется на благоприятный лепесток действия d2 и вновь надолго останется в нем. Однако за это «отступничество» ему придется накопить некоторый дополнительный штраф, которого не было бы, если бы всегда выполнялось действие d2.

На нашем рисунке в каждом лепестке ромашки по четыре состояния. Выбор этого числа состояний про­изволен. Каждый лепесток может содержать не четыре, а большее или меньшее число состояний. Обозначим это число через q. Оно называется глубиной памяти автомата. Смысл этого параметра заключается в следующем. Чем больше q, тем более инерционен автомат, ибо тем большая последова­тельность штрафов вынуждает его к смене действий. Интуитивно ясно, что, чем больше инерционность автомата, тем ближе он к тому, чтобы, выбрав на­илучшее в данной среде действие, продолжать вы­полнять только его.

85

Читателю должно быть ясно, что с ростом глубины памяти растет при функционировании в стационарных средах и целесообразность поведения автомата. И, наоборот, при малом значении q функционирование автомата подвержено воздействию сигналов штрафа, часто выводящих автомат на лепестки с невыгодны­ми действиями.

Конструкция автомата, рассмотренная нами, бы­ла названа М. Л. Цетлиным автоматом с линейной тактикой. И эта весьма простая в технической реа­лизации система (набор сдвигающих регистров, соот­носимых с лепестками и тривиальная логическая схема для организации сдвига единички в этих ре­гистрах и перехода с регистра на регистр) решает сложную задачу о целесообразном поведении в лю­бой заранее не фиксированной стационарной среде. Факт этот вызывает глубокое изумление. Сколь же просты оказываются конструкции, способные выпол­нять процедуры адаптации, представляющиеся на первый взгляд весьма сложными.

Но оказывается, что целесообразное поведение это еще не все. Можно показать (и М. Л. Цетлин сде­лал это), что если minP, не превосходит 0,5, то при росте величины q мы получим последовательность автоматов с линейной тактикой со все увеличиваю­щейся глубиной памяти, которая является асим­птотически оптимальной. Это означает, что при q -->бесконечность имеет место M(q,E) —>М, где М—минималь­ный суммарный штраф, который можно получить в данной стационарной случайной среде. Таким об­разом, во многих таких средах конструкция, предло­женная М. Л. Цетлиным, обеспечивает при достаточ­но больших значениях q поведение, сколь угодно близкое к наилучшему. А это уже совсем фантастично.

После автоматов с линейной тактикой было най­дено еще много конструкций зверушек, которые мог­ли вести себя целесообразно, а зачастую асимптоти­чески оптимально в любых стационарных случайных средах. О них мы расскажем ниже.

§ 2.4. «Личные» качества автоматов

Автомат с линейной тактикой аккуратен и педан­тичен. Неторопливо движется он по состояниям ле­пестков, отсчитывая число поступивших на его вход

36

н
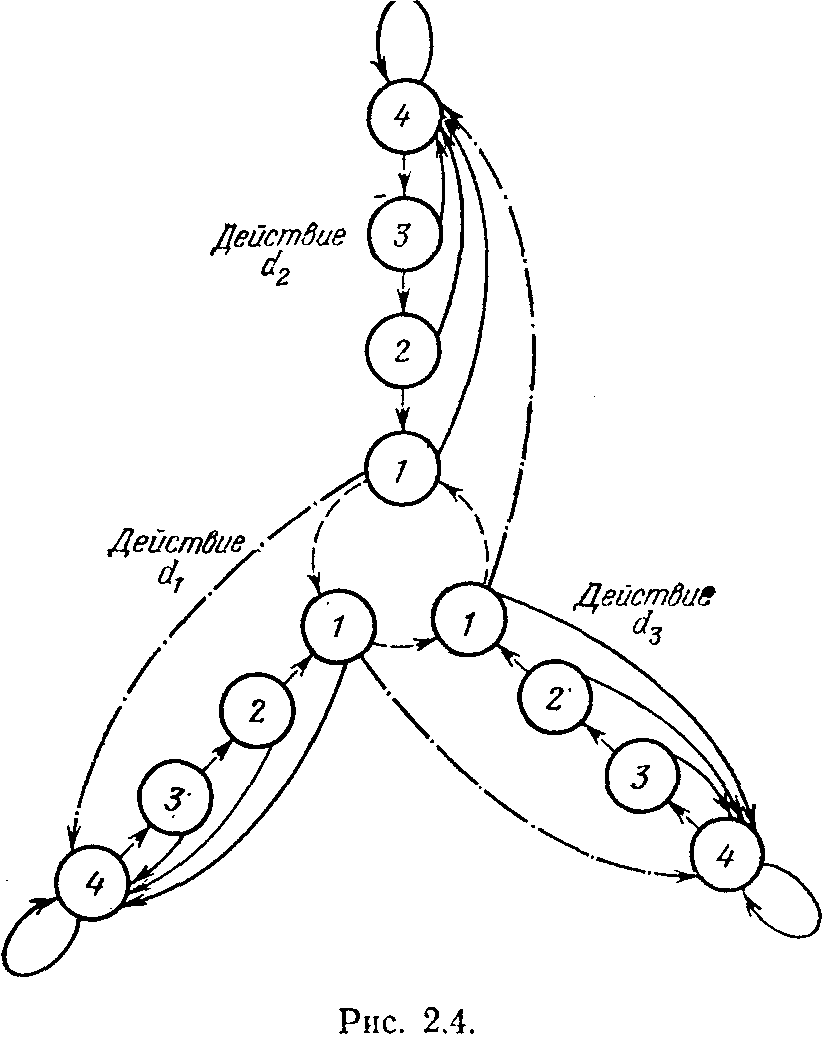
аказаний и поощрений. Но возможны и другие авто­маты. Вот один из них, предложенный В. И. Кринским. Он похож на автомат с линейной тактикой и действует при поступлении сигнала штраф аналогич­но автомату с линейной тактикой. Но при сигнале поощрение его поведение резко отлично от педан­тизма автомата с линейной тактикой. В каком бы

состоянии лепестка в этот момент не был автомат В. И. Кринского, он тут же меняет его на самое глу­бокое для данного лепестка состояние. Соответствую­щая картина показана на рис. 2.4 (пока не следует обращать внимание на штрихпунктирные линии). Такой автомат можно назвать «доверчивым». Он всегда «верит» в хорошее. И всякий положительный сигнал от среды приводит его в состояние «эйфории». Казалось бы, подобный способ поведения ничего кроме неприятностей автомату не сулит. Но мир ав­томатов оригинален и странен. Строго доказано, что доверчивые автоматы В. И. Кринского ведут себя

37

целесообразно в любых стационарных случайных сре­дах, а последовательность подобных автоматов с рос­том их глубины памяти q образует асимптотически оптимальную последовательность.

Оказывается, что и автоматы, предложенные Г. Роббинсом, которые отличаются от доверчивых ав­томатов тем, что при переходе с лепестка на лепесток они переходят не в начальное состояние лепестка, а в конечное его состояние (на рис. 2.4 эти переходы по­казаны штрихпунктирными стрелками), также ведут себя целесообразно в любой стационарной случайной среде и при росте глубины памяти q образуют асим­птотически оптимальную последовательность автома­тов. Создается такое впечатление, что любые меры по повышению инерционности автомата, задержке его в группе состояний, принадлежащих одному лепестку, улучшат качество его функционирования в среде. Пояснить это можно следующим примером. Заядлый рыболов, обнаружив однажды место, где был хоро­ший клев, может ходить сюда довольно долго, хотя результаты могут быть нулевыми. И часто при дос­таточном терпении он бывает вознагражден сторицей за предшествующие неудачи. А, сменив место ловли и не поймав ни одной рыбешки, такой рыболов не отчаивается и еще много раз приходит сюда, чтобы попытать счастья. И окончательно разочаруется в об­любованном месте лишь тогда, когда довольно много раз уйдет отсюда без какой-либо добычи. И, как по­казывает жизненный опыт многих поколений любите­лей рыбной ловли, средний улов такого рыболова всегда выше, чем у его коллеги, придерживающегося тактики менять место ловли, как только при первой же рыбалке его улов оказывается незначительным.

Опишем еще одну конструкцию автомата, обеспе­чивающего целесообразное поведение в любой ста­ционарной среде и дающего возможность построить асимптотически оптимальную последовательность ав­томатов, позволяющую получать минимальный воз­можный штраф в данной среде с любой наперед заданной точностью. В отличие от ранее рассмотрен­ных конструкций этот автомат будет не детермини­рованным, а вероятностным. Устроен он подобно ав­томату с линейной тактикой. При поступлении сиг­нала нештраф смена состояний в нем происходит так, как показано на рис. 2.3. Но при сигнале штраф та-

38

кой автомат не спешит менять состояние. Сначала он «подбрасывает монетку» и по результату подбрасы­вания либо переходит в состояние по пунктирной стрелке, показанной на рис. 2.3, либо сохраняет то состояние, в котором автомат получил сигнал штраф. Эта конструкция, предложенная В. Ю. Крыловым, может быть названа «осторожным» автоматом.

Интересен вопрос о том, насколько модели зве­рушек, построенные в рамках теории коллективного поведения, идентичны тем моделям, которые лежат в основе поведенческих актов, наблюдавшихся в опы­тах Торндайка, или в ситуациях альтернативного вы­бора, характерных для человека. М. А. Алексеев, М. С. Залкинд и В. М. Кушнарев провели серию экспериментов с людьми. Они проводили опыты в изолированной комнате, где ничего нет, кроме пуль­та с двумя кнопками, перед которым стоит стул. Ис­пытуемый садится на него и надевает наушники. Ес­ли нажать ту или иную кнопку, то с некоторой фик­сированной вероятностью, неизвестной испытуемым, в наушниках раздастся щелчок. Это сигнал поощре­ния. Отсутствие щелчка — аналог сигнала штраф. Цель испытуемого максимизировать сигналы нештра­фа путем правильного выбора нажимаемых кнопок. Внешне все выглядит так же, как в опытах Торн­дайка, т. е. альтернативный выбор из двух возмож­ностей и неизвестные заранее значения вероятностей поощрения и наказания. Как же ведут себя люди в этой экспериментальной ситуации? В простейших случаях, когда вероятность щелчка при нажатии одной из кнопок была равна единице, а при нажатии второй имелась ненулевая вероятность штрафа, люди быстро постигали ситуацию и нажимали лишь ту кнопку, которая гарантировала им стопроцентную удачу. Однако в более сложных случаях поведение испытуемых не было столь простым, как можно было бы предполагать.

Если стационарная среда задавалась, например, вектором Е == (0,2, 0,8), то, вместо того чтобы после некоторого периода обучения нажимать всегда пер­вую кнопку (здесь вероятность щелчка есть 0,8, так как вероятность штрафа для первой кнопки задана равной 0,2), человек нажимал то одну кнопку, то другую. На рис. 2.5 показан фрагмент действий ис­пытуемого. Верхняя цепь кружочков соответствует

39

н
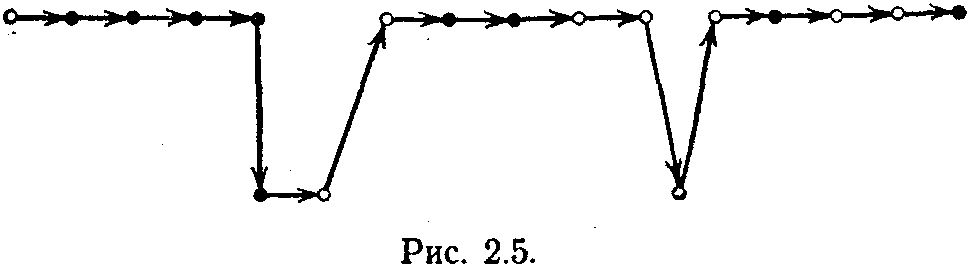
ажатию первой кнопки, а нижняя — второй кнопки. Зачерненные кружки соответствуют нажатию, при ко­тором испытуемый услышал щелчок, светлые — исхо­ду испытания со штрафом. Как видно из рисунка, испытуемый правильно считает, что надо нажимать на первую кнопку, но время от времени он пробует нажимать и на вторую. Появление штрафа при этом переходе с кнопки на кнопку (с лепестка на лепес­ток) приводит к возвращению к первой кнопке. Срав­нивая поведение людей с функционированием автома­тов с линейной тактикой, авторы эксперимента при­

шли к выводу, что людей можно уподобить таким ав­томатам с небольшой глубиной памяти (q = 1, 2, 3). Это приводит к тому, что люди решают задачу аль­тернативного выбора (особенно при близких значе­ниях вероятностей Pi друг к другу) хуже, чем авто­маты с линейной тактикой. И, конечно, хуже ос­тальных рассмотренных нами автоматов. Интересно, что И. Б. Мучник и О. Я. Кобринская показали, что крысы в условиях опыта Торндайка действуют с го­раздо большей глубиной памяти и превосходят в этом отношении человека. Но в средах с близкими значе­ниями вероятности штрафов за действия пальма пер­венства остается не за биологическими организмами, а за не знающими эмоций простейшими автоматными устройствами.