Варшавский В. И., Поспелов Д. А

Вид материала

Документы

Содержание 1—E сохранять их неизмен­ными с вероятностью E So автомата. Инициирующий сигнал поступает на край­ний автомат цепи А

Подобный материал:

• Герберт Александер Саймон Исследователи ии: Лотфи Заде Исследователи ии: А. А ляпунов,, 9.34kb.
• «Как привлечь средства государственных институтов развития» Варшавский Владислав Римович, 48.54kb.
• Аннотация к научно-образовательному материалу, 114.81kb.
• 141. Поспелов В. И., Стальнов В. С. Содружественная аккомодация глаз при дисбинокулярной, 167.36kb.
• Тезисы докладов участников III международного конгресса «Россия и Польша: память империй, 1372.37kb.
• Д. А. Поспелов, Г. С. Осипов, 487.33kb.
• Варшавский А. С. Следы на дне, 1828.32kb.
• Рабочая программа учебной дисциплины Для направления 080100. 62 «Экономика» (программа, 562.39kb.
• Диспут с Пирром: прп. Максим Исповедник и христологические споры VII столетия / Отв, 73.89kb.
• Программа дисциплины: Имитационные модели для направления Прикладная математика и информатика, 120.53kb.

§ 4.6. «Упрямые» автоматы и голосование

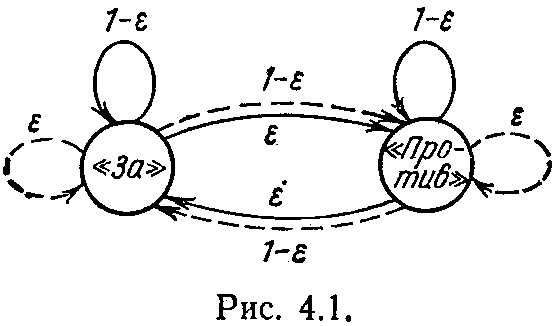
Дадим теперь формальную модель децентрализо­ванного согласования мнений. В традициях нашего изложения она будет описана на уровне функциони­рования коллектива автоматов. В' качестве членов этого коллектива будут выступать специальные «упрямые» автоматы. Простейший автомат такого типа показан на рис. 4.1. (На рис. 4.1 и 4.2, как и ранее, сплошными стрелками показаны переходы автоматов при сигнале поощрения, пунктирными — при сигнале наказания.) Как мы видим, упрямый автомат является вероятностным. У него два состоя­ния, которые соответствуют двум типам голосования («за» и «против»). Величина Эпсилон (E) характеризует степень

1

44


упрямства автомата. Если его штрафуют (например, «стыдят» его за то голосование, которого он придер­живался), то он с вероятностью 1—E принимает эту критику и меняет свое мнение. С вероятностью же E он продолжает отстаивать свою точку зрения. Если же его поощряют, то из-за своего упрямства с веро­ятностью E автомат все же в следующий тур голо­сования может сменить свой выбор.

Взаимодействие меж­ду автоматами в коллек­тиве мы организуем по следующему принципу, близкому к идее случай­ного взаимодействия: перед каждым туром го­лосования автоматы случайным образом разби­ваются на тройки (общее число автоматов, уча­ствующих в голосовании, будем для простоты считать кратным трем), в тройке с равной ве­роятностью выбирается один из автоматов и на его вход подается сигнал наказания, если его состояние не совпадает с состояниями двух других автоматов в данной тройке. В противном случае на его вход подается сигнал поощрения. Далее выбранный авто­мат с долей упрямства е производит смену своего мнения или сохраняет его. Эта операция проводится перед каждым туром голосования в новой случайно формируемой тройке и с новым случайно выбирае­мым автоматом в каждой тройке.

В каждой тройке происходит смена мнений (с известной долей упрямства) по принципу «как боль­шинство, так и я». Можно строго доказать, что коллектив таких автоматов выходит на статистиче­ски устойчивую точку, подобную точке Нэша. Доля автоматов, приходящих в нее, равна доле автоматов, ее покидающих. Если в исходном коллективе в пер­вом туре голосования большинство автоматов голо­совало «за», то эта точка такова, что и абсолютное большинство автоматов будет в ней голосовать «за». Если же исходное голосование было таково, что голосующих «против» было ощутимо больше поло­вины, то устойчивая точка будет нам демонстриро­вать абсолютное большинство голосующих «против». Когда в исходном состоянии доли автоматов,

145


голосующих «за» и «против», приблизительно равны, то выход в устойчивую точку будет происходить лишь при небольших значениях параметра упрямства E. Уменьшая его, можно добиться, чтобы коллектив все-таки вышел на устойчивую точку (даже один голос перевеса в начальной ситуации приведет к переходу нужной для абсолютного большинства части автоматов на это мнение).

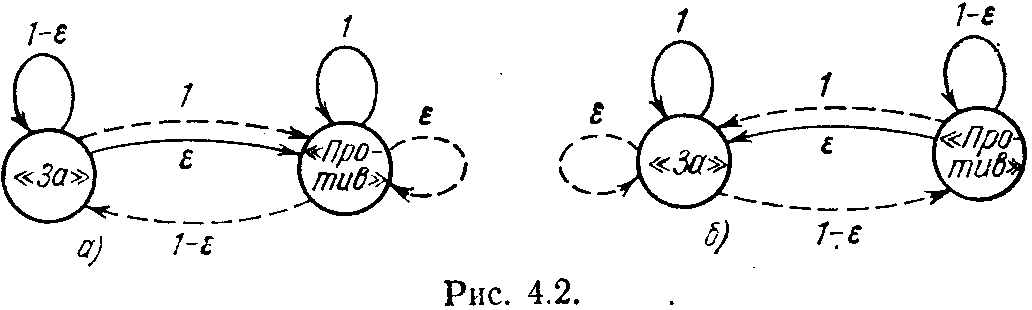
Наши упрямые автоматы были выбраны так, что они симметрично оценивали мнения «за» и «против». Психологические эксперименты, проведенные с людь­ми много раз, показывали, что для абсолютного большинства испытуемых этой золотой середины в выборе мнений не наблюдается. Одни более склонны принимать положительные альтернативы, голосуя «за», другие более склонны голосовать «против». Такую несимметричность легко привнести и в наши автоматы. Рис. 4.2 демонстрирует, как это можно


сделать. На рис. 4.2, а показана диаграмма смены состояний для упрямого автомата, предпочитающего голосовать «против», а на рис. 4.2, б — для любителя голосовать «за». В коллективе такие несимметрич­ные автоматы ведут себя аналогично симметричным. Их однородные совокупности выходят на такие же устойчивые точки, как и однородный коллектив из симметричных автоматов. Только скорость сходимости к ним будет несколько иной.

Естественно обсудить и модель неоднородного кол­лектива. Можно изучить два вида неоднородности. Во-первых, можно рассмотреть совокупность сим­метричных и несимметричных автоматов двух типов. Эксперимент на ЭВМ показал, что такой коллектив ведет себя подобно однородному. Обе устойчивые точки достигаются им успешно. Во-вторых, можно рассмотреть коллектив, в котором автоматы разли­чаются по степени своего упрямства. Параметр

1
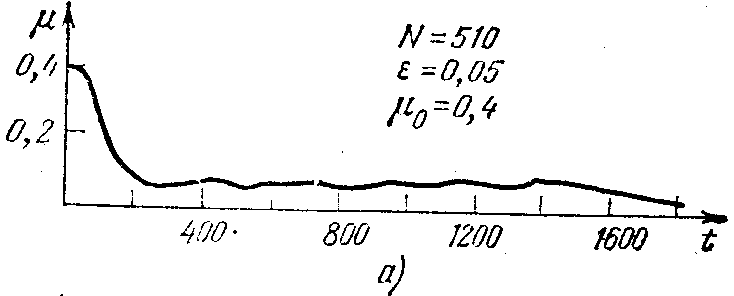
46


у
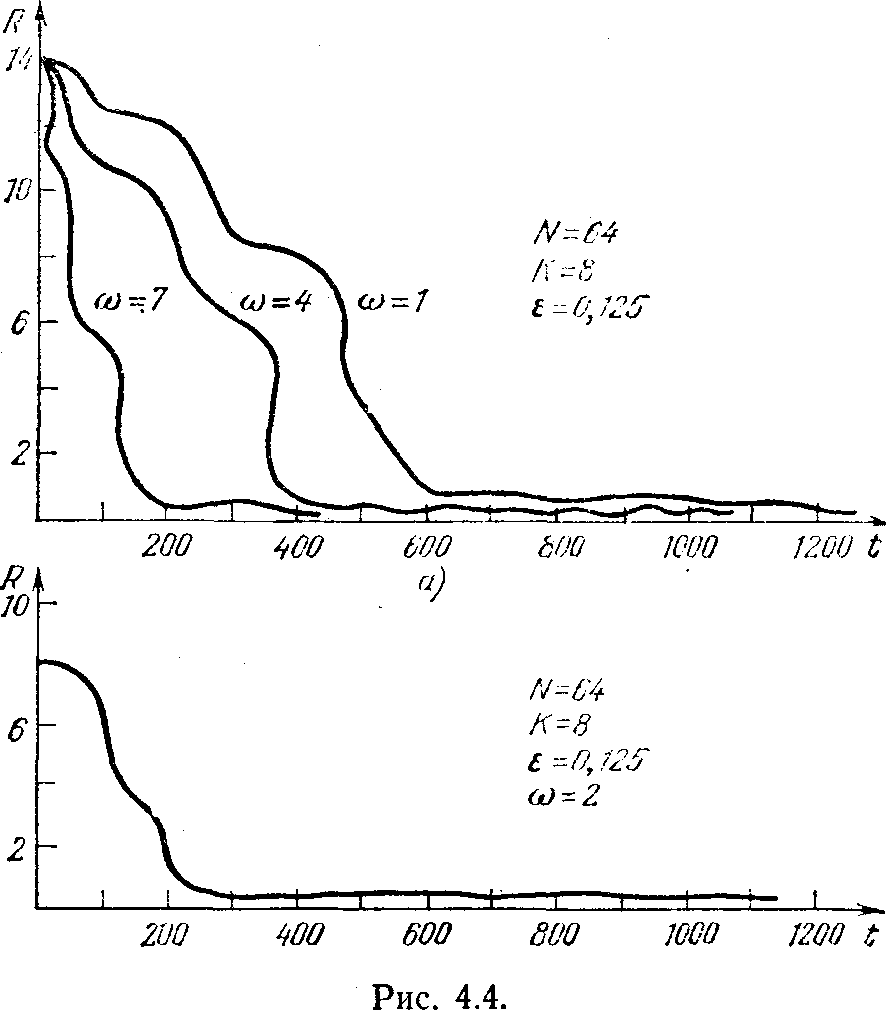
прямства для некоторого фиксированного автомата может принимать значения из множества {E1,E2, ..., En}. Но, как показывает эксперимент, и такой коллектив выходит либо на устойчивую точку, где абсолютное большинство голосует «за», либо на аналогичную точку, где абсолютное большинство го­лосует «против». На рис. 4.3 приведены типовые кривые, получаемые в результате моделирования. По оси абсцисс на этом рисунке отложены такты моделирования t (туры голосования), а по оси ор­динат Мю — доля автоматов в коллективе из N авто­матов, которая голосует «против» (Мю₀ — начальная доля таких автоматов). На рис. 4.3, а и 4.3,6 рас­смотрен однородный коллектив с разным числом автоматов в коллективе и разным начальным пред­почтением в коллективе голосующих. На рис. 4.3, в

147

п
оказан процесс моделирования для неоднородного коллектива, в котором имеется два типа автоматов, отличающихся по параметру своего упрямства.

Интересно отметить, что в отсутствие перемешивания в коллективе автоматов (например, при фик­сации для каждого автомата множества его возмож­ных соседей) эффект, который мы наблюдаем на рис. 4.3, становится недостижим. Это еще раз под­черкивает важность процедуры случайных взаимо­действий в «жизни» автоматных коллективов.

Выше мы рассмотрели простейшую модель голо­сования. Теперь от нее мы сможем перейти к модели, которая напомнит нам трудное заседание жилищной комиссии или парадокс «темной лошадки» Лошадкина при отборе работ на конкурсе. Наш коллектив, как и ранее, будет состоять из упрямых симметричных автоматов. Но теперь число состояний каждого авто­мата равно К, где К — число ранжируемых объектов. Если мы вспомним наш пример с конкурсной комис­сией из § 4.5, то там К=7 и каждый упрямый автомат, моделирующий некоторого члена конкурс­ной комиссии, должен иметь 7! состояний. Каждое состояние автомата есть некоторая фиксированная ранжировка объектов.

Предположим, что перед каждым туром голосо­вания происходит случайное разбиение коллектива автоматов на пары (т. е. осуществляется случайное парное взаимодействие). Если в коллективе нечетное число автоматов, то автомат, не вошедший в пару, в очередном туре голосования сохраняет свои пред­шествующие предпочтения. Для каждой пары вы­числяется значение рассогласованности предпочтений тех автоматов, которые попали в пару. Меру этой рас­согласованности ро можно подсчитать следующим об­разом. Пусть имеются два предпочтения (И, П, С, Л, К, М, Сб) и (Сб, И, М, Л, К, С, П). Б качестве объектов взяты претенденты на премии из примера § 4.5, а фамилии заменены первыми их буквами. Берем первый элемент из первой шкалы И и смотрим на каком месте он стоит во второй шкале. Во второй шкале он стоит на втором месте. Разность мест равна 1. Далее возьмем второй элемент первой шкалы П и снова смотрим, "на каком месте он на­ходится во второй шкале. В нашем случае он стоит на седьмом месте. Разность мест равна 5. Повторяем

148

этот процесс для всех элементов шкалы и суммируем получившиеся разности. Эта сумма и есть мера рассо­гласованности двух шкал. В нашем примере ро=1+5+3+0+0+3+6=18.

П
усть произведено разбиение множества автома­тов с их предпочтениями на N/2 пар (N — общее число автоматов в коллективе, если N—четно, либо число автоматов в коллективе без одного, если N—нечетно). Для каждой пары подсчитывается мера рассогласованности. Сумма этих мер, деленная на N/2, определяет R—меру рассогласованности мнений по коллективу автоматов. Именно она характеризует успешность или неуспешность коллективного голосова­ния. Если R=0, где R—мера рассогласованности по коллективу, то это означает, что у всех автоматов коллектива, состоящего из четного числа членов, все мнения полностью совпали.

Пусть в паре автоматов равновероятно выбирается один из них, который будет изменять свои предпоч­тения с вероятностью 1—E сохранять их неизмен­ными с вероятностью E. Как будет организовано изменение предпочтений? Автомат выделяет в мере рассогласованности тот элемент, который вносит в нее максимальное рассогласование. В том примере, кото­рый мы только что рассмотрели, таким элементом является Собакин. Его вклад в рассогласование, равный 6 единицам, самый большой. Тогда с вероят­ностью 1—E выбранный в паре автомат может переставить Собакина на несколько позиций так, чтобы рассогласование уменьшилось. Наиболее прост случай, когда перемещение происходит на соседнюю позицию. Тогда, если изменения производит второй автомат в паре, то ранжировка (Сб, И, М, Л, К, С, П) превращается в ранжировку (И, Сб, М, Л, К, С, П). Но можно осуществить перестановку и на большее число позиций. Число позиций, на которое переме­щается элемент, вносящий максимальное рассогласо­вание в ранжировки автоматов пары, можно назвать степенью «конформизма» автомата. После изменения предпочтений (или сохранения старых в тех парах, где проявилось упрямство) наступает новый тур голосования и образование в коллективе новых слу­чайных пар.

Моделирование на ЭВМ описанного процесса при различном числе автоматов, различном числе ранжи-

149


руемых элементов, различных, значениях параметра упрямства автоматов и степени конформизма пока­зало, что имеется явная тенденция сходимости про­цесса к некоторому единому мнению. На рис. 4.4 показаны типичные результаты моделирования. По оси абсцисс отложены такты моделирования t (туры голосования), а по оси ординат—значения R. На рис. 4.4,а показано поведение коллектива автоматов при различных степенях конформизма Омега. Видно, что увеличение степени конформизма приводит к ускоре­нию сходимости. В начальный момент мнения авто­матов в коллективе равномерно распределены по допустимым ранжировкам. На рис. 4.4,6 показан процесс сходимости в том случае, когда в начальной ситуации мнения автоматов не «размазаны» равно­мерно по всем возможным ранжировкам, а имеют вид нормального усеченного распределения на них. Этот случай ближе к реальности, чем предыдущий, так как в коллективе голосующих, как правило, уже перед первым туром наблюдается некоторое согласо-

150

ванное «общее мнение», по крайней мере относительно определенных претендентов. Как видно из рис. 4.4, скорость сходимости мнений экспертов при наличии предварительного общего мнения увеличивается.

Отметим, что модели голосования, которые мы рассмотрели, могут интерпретироваться в самых неожиданных областях. Например, модель простей­шего голосования «за» и «против» в коллективе автоматов тесно связана с созданием живучих тех­нических систем, в которых элементы способны к самовосстановлению. К этому мы еще вернемся в гл. 5.


Г л а в а 5. КОЛЛЕКТИВ ВО ВРЕМЕНИ


«Время уже оделось в числа»,

Луис де Гонгора

§ 5.1. Что такое синхронизация?

Уже довольно давно биологи, которые занимались культурами тканей, т. е. выращиванием живых кле­ток вне организма, обратили внимание на синхрони­зацию моментов деления клеток. Явление заключалось в следующем. Клетка делится. Две вновь образовав­шиеся клетки некоторое время находятся в состоянии покоя, а затем одновременно делятся. Тот же эффект повторяется для четырех вновь образовавшихся кле­ток и т. д. Возможны следующие механизмы, обеспе­чивающие синхронизацию делений. Во-первых, в каждой клетке могут существовать достаточно точные внутренние часы, которые определяют интервалы между делениями клетки. Во-вторых, клетки могут согласовывать друг с другом моменты своих делений. До сих пор ни одна из этих гипотез не нашла точ­ного экспериментального подтверждения. Первая гипотеза достаточно правдоподобна; если такие часы действительно существуют, то механизм синхрониза­ции очевиден. Для обеспечения механизма согласо­вания необходим обмен информацией между клет­ками. Существует возможность достаточно быстрого обмена сигналами, например при помощи биополя, но наличие такого биополя до сих пор нельзя считать экспериментально доказанным. Скорости же распространения электрохимических процессов, по-видимому, не могут обеспечить наблюдаемой точ­ности синхронизации достаточно больших популяций клеток. Последнее определило интерес биологов только к двум гипотезам, объясняющим механизм синхронизации — наличие биополя и внутренних часов. Существование биополя оставалось под большим сомнением, а внутренние часы могли объяснить только процесс синхронного независимого деления и также требовали рассмотрения механизмов взаимодействия, если включение процесса деления

152

инициируется каким-либо внешним для популяции клеток сигналом, воспринимаемым ограниченным числом клеток.

Описанный, но необъясненный эффект, возникаю­щий в изучаемом объекте, вещь неприятная, но не смертельная. Однако, как только ученые начали за­ниматься моделями самовоспроизведения, вопрос о механизмах, обеспечивающих одновременное вклю­чение разных частей самовоспроизводящейся машины, встал уже не перед биологами, а перед инженерами и математиками. Здесь, правда, вроде бы не было технической сложности — можно было иметь в си­стеме общие, достаточно точные часы и одновременно сообщать всем частям системы текущее время. Такой способ временного согласования поведения частей системы называется в технике синхронизацией. Однако идея синхронизации общих часов казалась далекой от биологических прототипов и американский ученый Дж. Майхилл сформулировал свою знамени­тую задачу, которая носит название «задачи о цепи стрелков». Задача Майхилла состоит в следующем:

Имеется цепь стрелков (рис. 5.1), каждый из которых может общаться только с двумя своими не­





посредственными соседями. Цепь состоит из конечного числа стрелков, два крайних стрелка имеют только по одному соседу. Один из крайних стрелков получает команду, после чего стрелки должны договориться и одновременно произвести выстрел. Существуют ли правила поведения стрелков, обеспечивающие реше­ние этой задачи, если количество слов, которыми могут обмениваться стрелки и объем внутренней памяти каждого из них ограничены и не зависят от длины цепи?

Положительный ответ на вопрос о существовании решения задачи Майхилла означает, что есть воз­можность синхронизации совокупности сколь угодно большого числа объектов ограниченной сложности за счет организации взаимодействия между ними при сколь угодно медленных процессах обмена сигналами.

153


Существование решения задачи Майхилла было доказано Дж. Мак-Карти и М. Минским, а в 1962 г. Э. Гото опубликовал решение задачи с минимально возможным временем решения, равным 2N—2, где N — число стрелков. При этом алгоритм поведе­ния каждого стрелка представлялся конечным авто­матом с несколькими тысячами внутренних состоя­ний. Следующий принципиальный шаг был сделан советским ученым В. И. Левенштейном, опубликовав­шим в 1965 г. блестящее решение задачи, в которой используется автомат, имеющий всего девять внут­ренних состояний. Усилиями последующих иссле­дователей число состояний удалось уменьшить до восьми.

Хотя решение задачи Майхилла давало ответ па принципиальный методологический вопрос и демон­стрировало ряд эффектов, которых мы коснемся в следующем параграфе, многие относились к полу­ченным конструкциям скептически: «Зачем городить все эти сложности, если можно протянуть провод меж­ду всеми стрелками и одновременно для всех вклю­чить лампочку, являющуюся командой стрелять?»

До последнего времени возражать таким скепти­кам было трудно. Принцип внешней синхронизации прекрасно обеспечивал решение огромного числа технических задач. Однако постепенно начали накап­ливаться представления, связанные с трудностями использования общей синхронизации в системах высокой сложности. Положение драматизировалось с появлением субмикронных интегральных схем. Дело в том, что если размер транзисторного перехода в кристалле меньше микрона, то задержки в соедини­тельных проводах становятся более существенными, чем время переключения транзистора, и мы опять попадаем в ситуацию, когда обмен информацией между объектами оказывается относительно медлен­ным. В обиход начал входить термин — эквихронная зона, т. е. зона кристалла, в которой можно считать, что время течет одинаково. Для обеспечения же синхронизации процессов, протекающих в различных эквихронных зонах, требуется организация специаль­ного взаимодействия между зонами.

Существуют разные подходы к решению этой задачи. Здесь мы остановимся на решении, связан­ном с задачей Майхилла.

154

§ 5.2. Управление стрелками

Сформулируем задачу Майхилла в терминах авто­матов, моделирующих поведение стрелков.

И
меется цепь из N автоматов. Каждый автомат имеет п внутренних состояний. Состояние каждого автомата в следующий момент времени зависит от его состояния в текущий момент времени и состояний двух его соседей, правого и левого. В начальный мо­мент все автоматы находятся в некотором начальном состоянии S_о. В начальный момент па один из край-них автоматов цепи подается внешний сигнал, выво­дящий его из начального состояния. Существует ли такая конструкция автомата (правила смены его состоянии), что после инициации крайнего автомата цепи через некоторое время все автоматы одновре­менно перейдут в одно и то же состояние S и ни один из них не перейдет в это состояние ни в один из предыдущих моментов, при­чем сложность каждого ав­томата п не зависит от дли­ны цепи.

Рассмотрим возможный алгоритм взаимодействия автоматов, обеспечивающий решение указанной задачи. На рис. 5.2 изображена временная диаграмма по­ведения цепи из девяти ав­томатов. Каждому автомату соответствует вертикальная

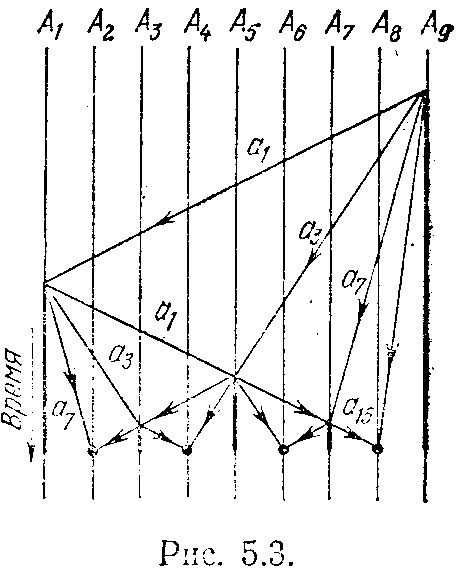
линия. Тонкая линия обозначает начальное состояние So автомата. Инициирующий сигнал поступает на край­ний автомат цепи А₉ и переводит его в состояние, ко­торое мы будем называть состоянием готовности S₁. Перейдя в это состояние, автомат посылает в цепь два сигнала а₁ и a₃, распространяющиеся по цепи со ско­ростями 1 и Уз соответственно. Распространение сигнала по цепи со скоростью 1 означает, что авто­мат, получивший справа сигнал а₁, передает его в том же направлении в следующем такте работы, а при скорости распространения 1/3 задерживает сигнал а₃ на три такта.

155


Сигнал a₁, дойдя до противоположного края цепи, переводит крайний автомат в состояние готовности Si и отражается от края цепи, начиная распростране­ние в обратном направлении (слева направо). Не­трудно понять, что отраженный сигнал а₁ и сигнал а₃ встретятся точно в середине цепи. Находящийся в точке встречи автомат A₅ (или два автомата в слу­чае их четного числа) переходит в состояние готов­ности Si, которому на рис. 5.2 соответствует жирная черта.

Автомат A₅, перешедший теперь в состояние S₁, посылает в обе стороны по паре сигналов a1 и a3, причем сигнал a1 отражается от первого встречен­ного им автомата в состоянии S₁. В результате в точках встречи отраженных сигналов с сигналом из (А3 и A7) происходит переход автомата в состоя­ние S₁ и наступает новая генерация сигналов a1 и a3 в обе стороны.

Т
аким образом, в каждом цикле происходит деле­ние интервала между двумя автоматами, находящи­мися в состоянии S₁ пополам, и в центре этого интер­вала автомат тоже переходит в состояние S₁. Такой процесс продолжается до тех пор, пока все автоматы цепи не перейдут в состояние S₁. Обратим внимание на то, что до последнего деления у каждого автомата будет по крайней мере один сосед, который не готов к синхронизации, т. е. находится в состоянии, отлич­ном от S₁. Автомат переходит в состояние синхрони­зации S, если он сам и оба его соседа находятся в состоянии S₁. Таким образом, задача синхронизации решается и правила поведения каждого автомата не зависят от длины цепи. Время, необходимое для ре­шения задачи деления интервала пополам, равно 3/2 его длины, и, следовательно, общее время синхрони­зации с точностью до постоянных, зависящих от четности и нечетности интервалов, равно утроенной длине цепи.

Процесс синхронизации можно ускорить, если автомат, перешедший в состояние готовности, по­сылает еще сигнал а7, распространяющийся со скоростью 1/7, и сигнал а15, распространяющийся со скоростью 1/15 (рис. 5.3). Причины, приводящие к ускорению процесса синхронизации в такой ситуа­ции, очевидны из сравнения рис. 5.2 и 5.3. Хотя и в этом случае правила локального поведения не

156

зависят от длины цепи, но сложность автоматов возрастает.

Для того чтобы отдельно взятый автомат мог осуществить задержку сигнала на Т тактов, необхо­димо, чтобы он имел не менее Т внутренних состоя­ний. Если он одновременно должен задерживать один сигнал на Т1 тактов, а другой сигнал на Т₂ тактов, то число его состояний должно быть не меньше, чем T₁T₂. Таким образом, введение допол­нительных сигналов, ускоряющих синхронизацию, ведет к существенному росту сложности автоматов. Кроме того, теперь необхо­димое число сигналов, а следовательно, и сложность автоматов начинает зави­сеть от длины цепи.

В предыдущем парагра­фе мы уже упоминали о блестящем решении задачи синхронизации В. И. Левенштейном. Необычайное изящество этого решения состоит в том, что он на­шел способ организовать взаимодействие между авто­матами так, что в про­цессе взаимодействия между соседними автоматами осуществляется задержка распространения сигналов на число тактов, равное 1, 3, 7, 15, ..., (2^k—1), причем k зависит не от числа состояний автомата, а от длины цепи. Решающие эту задачу автоматы имели всего девять внутренних состояний. Сейчас известно решение для восьми внутренних состоянии. В этом случае время синхронизации достигает свое­го минимального значения, равного удвоенной длине цепи, т. е. времени, необходимого для того, чтобы сигнал, распространяющийся со скоростью 1, про­шел всю цепь туда и обратно.

Методологически принципиально в этом решении то, что за счет взаимодействия каждый автомат решает локальную задачу, сложность которой та­кова, что без взаимодействия сам автомат не может се решить и, более того, с ростом числа автоматов при сохранении ограниченности взаимодействия

157


только двумя соседями растет сложность решаемых локальных задач.

Появление решения задачи Майхилла породило несколько дополнительных интересных проблем. Прежде всего была решена задача синхронизации цепи автоматов для случая инициации произвольного автомата цепи. Сложность локального автомата при этом возросла до 10 состояний.

Следующий вопрос, возникший при развитии мо­делей этого типа,— вопрос о возможности синхрони­зации двух автоматов, между которыми включена неизвестная им задержка, причем сложность авто­матов не должна зависеть от величины задержки. Последнее требование исключает возможность ис­пользования простого алгоритма, сводящегося к на­хождению временного интервала между посылкой сигнала и возвращением отраженного сигнала об­ратно. Использование указанного алгоритма не­возможно и в случае, если задержка изменяется во времени — например, в такой полуфантастической ситуации, когда мы хотим синхронизовать события на Земле и удаляющемся от нее космическом кораб­ле. В этой ситуации мы должны синхронизовать систему, посылая друг другу сигналы синхронизации в один и тот же момент. Возникает вопрос о суще­ствовании алгоритма выхода на синхронный режим за счет локального поведения командного комплекса на Земле и систем космического корабля. В рамках рассматриваемых автоматных моделей решение оказалось достаточно простым и обеспечивается автоматами, имеющими 12 внутренних состоянии.

Идея алгоритма, осуществляющего синхрониза­цию с точностью до такта автомата, достаточно про­ста и состоит в следующем. Инициирующей синхро­низацию автомат посылает в канал связи в три последовательных момента времени три сигнала a1, a2 и a3. Приемник отправляет эти сигналы обратно, задержав сигнал а1, на один такт, сигнал a2 на два такта и сигнал a3, на три такта. Одновре­менный прием одним из участников обмена сигна­лов a1 и a3 означает выход на синхронный режим, и с этого момента он начинает посылать в канал синхросигнал s. В момент совпадения у одного из участников сигналов a1 и a3 другой участник полу­чает сигнал a2, который отправляет обратно с за-

158

держкой в два такта. После выхода на синхронный режим сигнал a2 не отличим от сигнала s, и если последний возвращается участником с задержкой в два такта, то обмен сигналами s начинает поддер­живать взаимную синхронизацию. Для исключения влияния неточности локальных часов, определяющих локальное время на Земле и космическом корабле, обмен сигналами a1 и a2 должен продолжаться и после выхода на синхронный режим.

Т
еперь рассмотрим ситуацию, в которой майхилловские стрелки не стреляют из ружей, а включают какие-то устройства (рис. 5.4), каждое из которых обладает своим латентным временем, т. е. временем между нажатием пусковой кнопки и началом работы устройства. Например, от момента включения пи­тания радиолокационной станции до момента разо­грева радиоламп проходит 1 мин, а от момента за­пуска двигателя до его прогрева — 5 мин. Каждому «стрелку» известно только латентное время своего собственного устройства. Возникает вопрос о су­ществовании локальных правил поведения автоматов, сложность которых (число состояний) не зависит ни от длины цепи, ни от латентных времен других «стрелков», иными словами, после подачи команды одному из «стрелков» цепи они должны нажать пусковые кнопки так, чтобы все управляемые ими устройства начали работать одновременно.

Оказалось, что эта задача имеет решение, бази­рующееся на принципах решения исходной задачи Майхилла и локальный автомат представляет собой цепочку из T_k автоматов, решающих задачу Майхил­ла, где T_k — локальное латентное время, и логиче­ской схемы, вырабатывающей стартовый сигнал в зависимости от состояний автоматов указанной цепочки.

159


Коль скоро мы рассматриваем алгоритмы локаль­ного ограниченного взаимодействия, то естественно задуматься о влиянии на решение задачи числа соседей. При изучении этого вопроса оказалось, что решение задачи синхронизации не на отрезке, а на произвольном графе, приблизительно так же сложно. С другой стороны, возникает вопрос, а может ли быть решена задача синхронизации не при двух, а только при одном соседе? Ответ на этот вопрос положителен. Любая задача, которую можно решить на отрезке с двумя соседями, можно решить на кольце с одним соседом.