Варшавский В. И., Поспелов Д. А

Вид материала

Содержание

Рii характеризуют вероятность того, что на следующем шаге автомат будет взаимодействовать с той же средой ei
М* — время жизни автомата с начальным состоянием j при оптимальном переключении им сред, d(i) —

Подобный материал:

1 2 3 4 5 6 7 8 9 ... 13

§ 2.5. Как жить в динамическом мире?

До сих пор мы рассматривали стационарную среду. Этакий застывший и неизменный мир. Такой мир возможен только в эксперименте. А в жизни любое животное живет в постоянно меняющейся среде. И задача выживания в динамическом мире куда слож-нее, чем адаптация к застывшему навеки стационарному миру. Законы изменения параметров внешней среды могут быть самыми различными. Трудно даже

40

Перечислить их виды. Поэтому при описании динамической среды мы поступим следующим образом. Рассмотрим k различных стационарных сред E1, E2, ..., Ek. И будем считать, что каждая такая среда представляет собой как бы мгновенную фотографию состояния динамической среды. Эти фотографии, меняясь, как кадры кинофильма, воссоздадут нам динамическую среду. На рис. 2.6 показано взаимодействие автомата с таким миром.

К

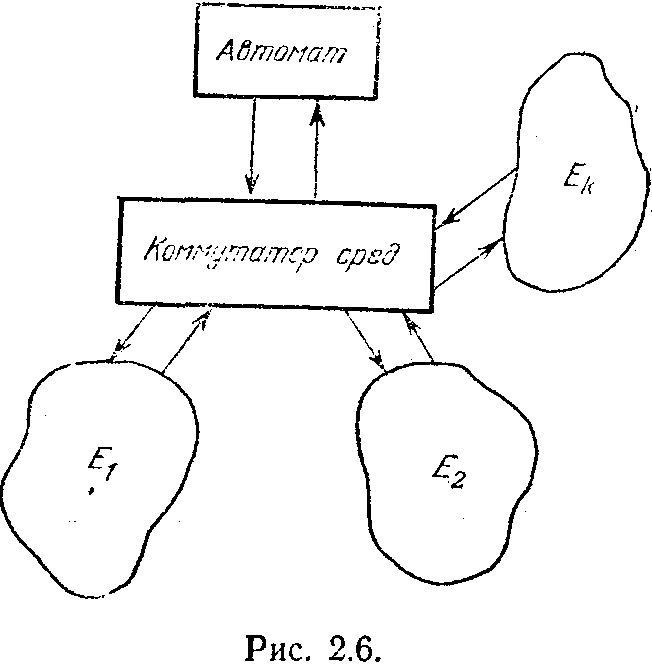
оммутатор как бы подключает зверушку к той или иной стационарной среде. Как характеристики этих сред, так и законы работы коммутатора автомату заранее неизвестны. Адаптация состоит теперь не только в оценке значений Рi в степени m, где верхний индекс характеризует среду Ет, а и в определении закономерности смены сред коммутатором.

В' дальнейшем мы рассмотрим лишь один частный случай работы коммутатора. Связано это с тем, что в теории коллективного поведения именно он оказался изученным наиболее глубоко. Остальные более сложные случаи еще ждут своего анализа. Предположим, что коммутатор производит подключение стационарных сред на основании некоторой таблицы (матрицы), имеющей k строк и k столбцов. Элемент Pij, стоящий на пересечении i-й. строки этой таблицы и ее j-го столбца, есть вероятность того, что после среды Ei, воздействовавшей на вход автомата, к нему будет подключена среда Ej. Элементы вида

41

Рii характеризуют вероятность того, что на следующем шаге автомат будет взаимодействовать с той же средой ei, что и на предшествующем шаге. Подобную динамическую среду можно назвать переключающейся. Если подбирать значения Рij надлежащим образом, то переключающаяся среда может достаточно хорошо описывать многие динамические среды.

Что же изменяется при переходе зверушки в переменчивый мир переключающейся среды? Остаются ли верными те основные положения, которые мы смогли постулировать при описании поведения в застывших стационарных мирах?

Рассмотрим сначала ситуацию, часто встречающуюся в русских народных сказках. Иванушка-дурачок встречает свадьбу. И он начинает громко причитать и плакать. Такое неадекватное поведение вызывает мгновенную реакцию. Жестоко битый Иванушка через некоторое время встречает похоронную процессию. Помня о своей неудаче, он начинает весело смеяться и плясать. И снова жестокая кара постигает простодушного героя. Он снова бит. Если свадьбы и похороны чередуются в строгом порядке, а Иванушка-дурачок имеет единичную глубину памяти, то, как показывает схема на рис, 2.7,

б

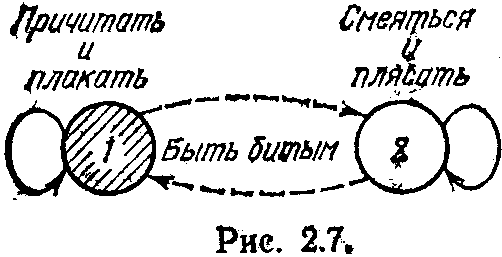
ыть ему всегда битому. Ибо действует он в противофазе с работой коммутатора, переключающего среду Ei = (l, 0) на среду Е2 = (0, 1) так, что каждый раз действие Иванушки вызывает сигнал наказания С вероятностью, равной единице. Если бы коммутатор переключал среды не жестко детерминированно, а с некоторыми вероятностями, то на долю Иванушки выпадали бы и счастливые минуты. Он причитал и плакал бы на похоронах, а смеялся и плясал на свадьбах, хотя и в этих условиях ему приходилось бы попадать в глупое положение и быть битому. Первое, что приходит в голову при анализе тяжелой судьбы Иванушки, это то, что он действует, как автомат с малой глубиной памяти. Он не обладает инерционностью, которая была благом для автоматов, действующих в случайных средах. Но правы ли мы были, если бы поторопились с таким заключением?

42

В

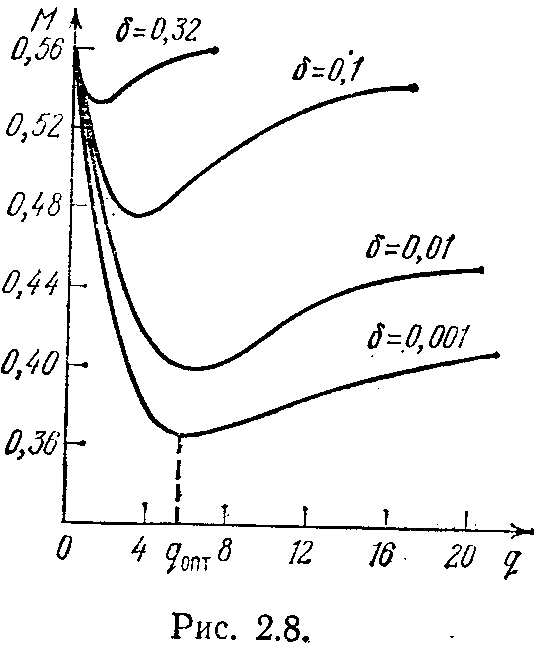
едь если в динамическом мире смена ситуаций происходит с большой частотой, то инерционность вряд ли может служить хорошим средством для существования в этом мире. В'едь в динамическом мире надо быстро, оперативно следить за возникающими изменениями среды. И для каждого динамического мира нужна своя наилучшая глубина памяти, выбранная в зависимости от скорости изменения обстановки, а вовсе не по принципу «чем больше, тем лучше». Это означает, что не приходится и мечтать о том, что рассмотренные нами конструкции зверушек будут вести себя целесообразно во всех динамических средах. И эксперименты неумолимо свидетельствуют об этом. На рис. 2.8 можно увидеть результаты одного такого эксперимента. Он проводился с помощью ЭВМ. Испытывались автоматы с линейной тактикой, имеющие различное число состояний в лепестках. Для простоты считалось, что автоматы могут выбирать

одно из двух действий. Переключающаяся среда была устроена тоже достаточно просто. Она состояла из двух стационарных сред, отличающихся друг от друга перестановкой вероятностей штрафов за действия (и этим она была похожа на пару сред в сказке об Иванушке-дурачке). В первой среде за первое действие вероятность штрафа была весьма велика, а за второе действие мала. В другой среде эти вероятности относились уже ко второму и первому действиям, т. е. ситуация была обратной. Обозначим через б вероятность смены сред (значения этого параметра надписаны над кривыми, показанными на рис. 2.8). По оси абсцисс отложена глубина памяти автомата, а по оси ординат — математическое ожидание накапливаемого штрафа.

Результаты эксперимента ясно показывают, что для каждого значения б существует своя оптимальная глубина памяти автомата с линейной тактикой, при

43

которой накапливаемый штраф минимизируется. Аналогичную картину можно наблюдать и при использовании в переключающейся среде автоматов других конструкций, целесообразно ведущих себя в стационарных случайных средах.

Итак, в динамических средах найденные нами конструкции автоматов оказываются не самыми лучшими. И единственный выход из этого положения — использовать какую-нибудь гибкую конструкцию, которая изменяется вместе с тем миром, где она функционирует.

Ученики и продолжатели дела М. Л. Цетлина предложили несколько конструкций зверушек, способных целесообразно функционировать в динамических средах. Самой известной из них является предложенная одним из авторов этой книги модель автомата с переменной структурой.

Предположим, что вы на своей автомашине ежедневно добираетесь из дома на работу. В вашем распоряжении есть два возможных маршрута, и вы вольны выбирать любой из них. Так как вы всегда выезжаете в одно и тоже время, то обстановка на каждом из маршрутов как бы стационарна. И, анализируя эту обстановку, вы убедились, что один из маршрутов лучше другого: времени тратится меньше — движение здесь менее интенсивное, чем по другому маршруту, да и светофоров не так много. Но вот беда. Время от времени из-за каких-то строительных работ движение здесь резко снижается, образуются пробки, и можно потерять много времени, пока они ликвидируются. В этих условиях данный маршрут становится намного хуже другого. Вы бы потеряли куда меньше времени и не опоздали бы на работу, выбрав в эти неудачные дни другой маршрут. Если нет никакой информации о частоте строительных работ на трассе первого маршрута, то при выезде из дома нет никаких шансов угадать, по какому маршруту лучше сегодня ехать. Однако день за днем вы накапливаете некоторую информацию. Учитесь на своем горьком опыте. Выясняется, что чаще всего пробки образуются в среду и пятницу и вероятность этих пробок достаточно велика. Тогда, выбирая в остальные дни недели первый маршрут, вы в среду и пятницу без колебаний выбираете менее хороший маршрут поездки.

44

Этот пример мы привели для того, чтобы у читателя возникли необходимые ассоциации с поведением автомата с переменной структурой в переключающейся среде. Опишем теперь его структуру и функционирование на более строгом уровне.

В

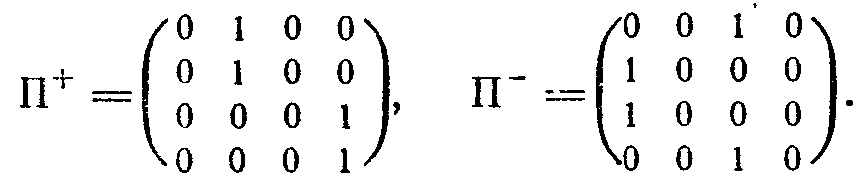
ернемся снова к автомату с линейной тактикой показанному на рис. 2.3. Его структура может был задана в виде двух матриц, определяющих смену состояний при получении сигнала нештраф и при получении сигнала штраф. Каждая такая матрица содержит 12 строк и 12 столбцов по числу различных состояний автомата. И в каждой строке этих матриц имеется одна единица, показывающая, как осуществляется переход. Выписывание этих матриц слишком громоздко. Поэтому вместо автомата с четырьмя состояниям

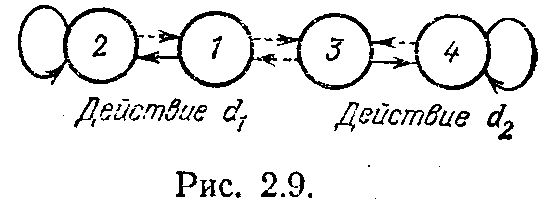
и в каждом лепестке и тремя действиями рассмотрим автомат с линейной тактикой с двумя состояниями в лепестке и двумя действиями (рис. 2.9) Для такого автомата матрицы имеют вид

Эти матрицы определяют детерминированную структуру нашего автомата. Если автомат вероятностный (как, например, упоминавшийся нами автомат В. И. Крылова), то вместо единиц и нулей в матрицах П+ и П- будут стоять значения вероятностей смены состояний. Если, например, автомат с линейной тактикой, показанный на рис. 2.9, заменить автоматом В. И. Крылова, то соответствующие матрицы примут вид

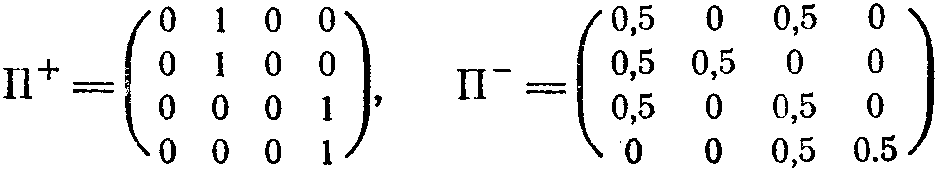
В отличие от детерминированного и вероятностного автоматов, у которых матрицы П+ и П- в процессе их функционирования остаются неизменными, для

45

автомата с переменной структурой П+ и П- не постоянны. В зависимости от результатов функционирования (наказаний или поощрений, получаемых от среды) автомат меняет свою структуру.

В

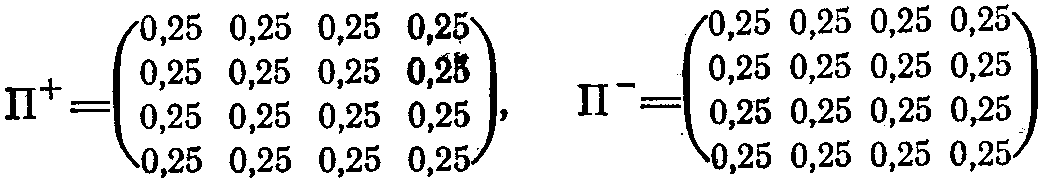
начальном периоде своей работы такой автомат находится в «безразличном» состоянии, когда вероятности всех переходов между состояниями для него абсолютно одинаковы. Для условий, показанных на рис. 2.9, это соответствует тому, что начальный вид матриц смены состояний для автомата с переменной структурой задается следующим образом:

Пусть для определенности начальным состоянием автомата было состояние с номером 1 и автомат, выполнив действие d1, соответствующее этому состоянию (см. рис. 2.9), с помощью равновероятного выбора по матрице П+ перешел в состояние 4. И пусть после этого он получил сигнал штраф. Получение подобного сигнала заставляет автомат считать свой переход 1-->4 при нештрафе за действие d1 ошибкой. Эта информация фиксируется следующим образом. Вероятность П14+ уменьшается на некоторую величину А. Но сумма вероятностей в любой строке матрицы должна быть равна 1, и поэтому уменьшение П14+ на Дельту должно привести к увеличению всех

о

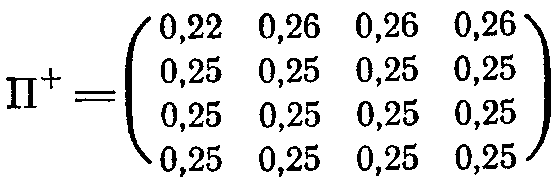
стальных вероятностей в этой строке, например, на величину Дельта/3, что позволит сохранить нормировку строк. Если взять Дельта== 0,03, то после этого шага матрица П- останется прежней, а матрица П+ примет вид

На очередном шаге автомат делает действие d2, соответствующее состоянию 4, и выбирает очередное состояние на основании матрицы П- (так как в текущем акте общения со средой он находится в условиях последнего сигнала от среды—штрафа).

46

Пусть он выбрал переход 4—>4 и вновь получил штраф. Теперь уже меняется матрица П-, а матрица П+ остается неизменной. В матрице же П- четвертая строка приобретает вид (0,26 0,26 0,26 0,22). На очередном шаге взаимодействия автомат опять использует вероятностный переход по матрице П-, и в зависимости от оценочного сигнала меняются значения вероятностей в четвертой строке матрицы и совершается очередной выбор либо по матрице П- (если последний пришедший оценочный сигнал был наказанием), либо по матрице П+.

Так постепенно происходит перестройка матриц П+ и П- в зависимости от сигналов, формируемых средой. Возникает вопрос: будут ли эти матрицы стремиться к какому-нибудь устойчивому значению, например к матрицам из нулей и единиц, соответствующих автомату с линейной тактикой, или какому-либо другому автомату, целесообразно ведущему себя в стационарных случайных средах? Если бы ответ был положительным, то это означало бы, что из механизма случайного выбора мы могли бы. формировать структуру зверушки, целесообразно функционирующей в статических случайных средах. Конечно, тот или иной ответ на поставленный нами вопрос зависит от тех законов изменения элементов в П+ и П-, которые мы будем использовать.

Что же показали проведенные исследования? Оказалось, что линейные законы изменения переходных вероятностей Пij в матрицах П+ и П-, описанных выше, не всегда приводят к оптимальным конструкциям, подобным автоматам В. И. Кринского или Г. Роббинса. Но если ввести нелинейное изменение элементов указанных матриц, то исходные «размазанные» матрицы с одинаковыми значениями Пij сходятся к матрицам из нулей и единиц, соответствующих автоматам, наилучшим образом ведущих себя в стационарных случайных средах.

Но не это главное. В стационарных случайных средах нет нужды тратить время на обучение автомата с переменной структурой, ибо заранее известны конструкции, успешно решающие в этих средах поведенческие задачи. Главное — поведение в динамических и, в частности, в переключающихся средах. Что дает использование автоматов с переменной структурой здесь?

47

Вернемся к рис. 2.8. Как мы уже знаем, для авто--матов с линейной тактикой существует оптимальное значение глубины памяти, зависящее от скорости переключения стационарных сред, при котором суммарный штраф, накапливаемый автоматом, становится минимальным. Но глубина памяти тесно связана с вероятностью пребывания автомата на том или ином лепестке и, следовательно, с вероятностью выполнения того или иного действия. Для автоматов с переменной структурой экспериментально (путем моделирования перестройки их структуры на ЭВМ) получен следующий фундаментальный результат:

с течением времени функционирование автомата с переменной структурой в переключающихся средах, в которых автомат с линейной тактикой действует целесообразно, неограниченно приближается к функционированию автомата с линейной тактикой, обладающему оптимальной глубиной памяти. Другими словами, автомат с переменной структурой сам находит эту оптимальную глубину памяти. Это весьма важно, так как значение qопт, показанное на рис. 2.8, нельзя априорно определять аналитическим путем, а оно должно подбираться в процессе функционирования в среде, на что автомат с линейной тактикой просто неспособен.

И еще одно. Вспомним наш пример с Иванушкой-дурачком. Нетрудно подобрать многочисленные примеры переключающихся сред, в которых эффект непрерывного битья все время будет преследовать автомат с линейной тактикой. Только он подстроится под определенную среду, как среда уже изменилась, и битье продолжается. Для этого достаточно условия, что среда переключается быстрее, чем автомат покидает свой лепесток и переходит на другой. Если бы заяц менял окраску шкурки в противофазе со сменой зимы и лета, затрачивая на это время, соизмеримое с полугодом, то он давно бы исчез с лица земли. Для автомата с переменной структурой подобного положения не существует. Как было сказано в одной из первых работ по таким автоматам, «миниальный штраф выплачивается в том случае, когда за вчерашние грехи сегодня награждают и в том случае, когда грехи остаются грехами».

В заключение этого параграфа приведем результат одного эксперимента с автоматом с переменной

48

структурой, имеющим восемь состояний и моделирующим поведение в среде, в которой автомат с линейной тактикой имел бы оптимальную глубину памяти, равную двум. Этот результат приведен на рис. 2.10. По оси абсцисс на этом рисунке отложено число тактов взаимодействия автомата со средой, а по оси ординат — средняя величина штрафа в расчете на одно взаимодействие. Горизонтальная пунктирная прямая соответствует значению м

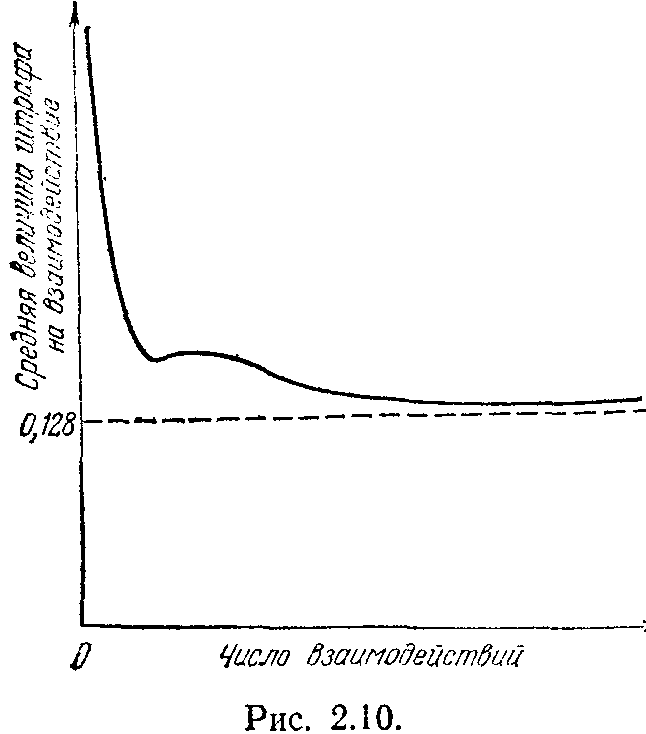
атематического ожидания штрафа для автомата с линейной тактикой с глубиной памяти, равной двум. Как мы видим, автоматы с переменной структурой на начальном этапе весьма быстро приближаются к наилучшему режиму работы автомата с линейной тактикой, а потом неуклонно асимптотически стремятся к этому оптимуму.

Такая явная связь между автоматами с линейной тактикой и с переменной структурой наводит на мысль о естественности этих конструкций, об их «эволюционной» связи.

И еще одно интересное наблюдение. Автомат с переменной структурой все время стремится уйти от штрафа, уйти в область благоприятных для себя действий. Это значит, что он чаще получает поощрения, а не наказания (если только среда не устроена так, что наказания в ней имеют значительно большую

49

вероятность, чем поощрения). А это в свою очередь означает, что матрица П+ изменяется сильнее, чем П-. Автомат как бы настраивается на хорошее функционирование в благоприятных мирах. К функционированию в таких условиях он лучше адаптирован.

Поведение автоматов в стационарных средах мы сравнивали с результатами экспериментов по альтернативному выбору решений людьми. Аналогичные эксперименты были проведены теми же авторами (М. А. Алексеев, М. С. Залкинд, В. М. Кушнарев) и в случае переключающихся сред. В процессе эксперимента по нажатию кнопок без ведома испытуемого происходило переключение среды. Если в предшествующий период (75—100 нажатий кнопок) имела место среда с E1==(0,8, 0,2), то на следующий период нажатий она сменялась на среду с Е2==(0,2, 0,8). Каков же результат этого эксперимента? Вывод, к которому пришли экспериментаторы, оказался парадоксальным. Человек в среднем лучше решает задачу адаптации к переключающейся среде, чем задачу для стационарной среды. Вернемся снова к рис. 2.5. При решении задачи в случае стационарной среды человек время от времени отказывается от хорошего выбора и как бы пробует, что получится, если сменить стратегию. И это характерно для любого испытуемого. Что кроется за этим феноменом? Наиболее ярко он проявляется, когда предпочтительность того или иного выбора близка к предельной. При близких вероятностях штрафа за выбор кнопки уходы с предпочтительной стратегии более редки. А чем яснее и проще решение, тем менее устойчиво поступает человек. Какая особенность его психики скрывается за этим? Почему в стационарной среде с Е = (0,8, 0,2) процент поощрений равен 62%, а в переключающейся среде, где E2 =(0,2, 0,8), он равен 72%? И это только на 1% ниже того, что достигает в данной динамической среде автомат с линейной тактикой с оптимальной глубиной памяти. Ответов на поставленные вопросы пока нет. Это еще один аргумент в пользу того, что поведение человека зачастую не только не оптимально, но и нецелесообразно. В сложном мире от зверушки до человека огромная качественная дистанция.

50

§ 2.6. «Доживем до понедельника»

Так назывался известный фильм из школьной жизни. Но то, о чем мы хотим поговорить здесь, ничем кроме названия не ассоциируется с этим давним фильмом. У нас речь пойдет о возможности организации зверушкой такого управления внешней средой или приспособления к ней, которое обеспечивает ей максимальный срок «жизни». Однако прежде нам нужно дать содержательную постановку задачи, а уже затем ее формальное описание.

Биологами хорошо исследована модель охоты летучих мышей, в частности, охота на ночных бабочек, способных воспринимать локационный ультразвуковой сигнал летучих мышей. Экспериментальный материал, относящийся к этой ситуации, можно суммировать следующим образом.

Летучая мышь испускает с помощью своего голосового аппарата направленный ультразвуковой сигнал. Встретив препятствие, сигнал отражается от него. Летучая мышь способна улавливать отраженный сигнал и с большой скоростью и точностью различать и идентифицировать его, что позволяет отличать неподвижные цели от подвижных, отражения от поверхности земли от отражений от воздушных целей, большие размеры от малых (например, отраженные сигналы от летящих птиц и комаров). Кроме того, отраженный сигнал позволяет летучей мыши с весьма большой точностью определять направления и расстояния до потенциальных целей.

Ночные бабочки в свою очередь способны принять локационный сигнал летучей мыши, определить местоположение источника, из которого был послан сигнал, а также определить интенсивность последнего. Поведение ночной бабочки различно в зависимости от того, как далеко от нее находится летучая мышь и сколь интенсивен сигнал. Если расстояние достаточно велико или интенсивность мала, то ночная бабочка производит маневр, направленный на уход от летучей мыши. В экспериментальных ситуациях наблюдалось три способа выполнения такого маневра. Либо бабочка разворачивалась и двигалась в сторону, противоположную своему предшествующему движению, либо она использовала маневр

51

в вертикальной плоскости, уходя со своего прежнего курса вверх или вниз. Если же расстояние до летучей мыши было мало или интенсивность локационного сигнала была очень велика, то ночная бабочка переходила на хаотический полет. Это происходит потому, что органы слуха бабочки в таких условиях начинают работать в режиме насыщения, и бабочка уже не может определить положение летучей мыши и направление ее движения. Хаотический полет состоит из чередования пассивного падения со сложенными крыльями, крутых поворотов, петель, пикирования. Другими словами, бабочки переходили на такую траекторию полета, которая максимально затрудняла для нападающего предсказание последующей точки на этой траектории. Интересно, что, как показывают эксперименты, более чем в 70% случаев хаотическое движение оказывалось для ночных бабочек спасительным.

Попробуем формализовать описанную ситуацию, несколько упростив ее. Это упрощение не является принципиальным. На основе той упрощенной модели, которую мы опишем, ряд исследователей построил совсем не игрушечные модели «преследуемый — преследователь», в том числе и для моделирования поведения ночной бабочки, спасающейся от летучей мыши.

Посмотрим на рис. 2.11. На нем изображен граф смены состояний некоторого вероятностного автомата. Его особенность состоит в том, что для каждой группы состояний (на рисунке группы состояний оконтурены пунктирными линиями) имеется ненулевая вероятность перейти в особое состояние, в котором автомат погибает (на рисунке оно заштриховано). Состояния можно интерпретировать, например, следующим образом: 1 — летучая мышь производит поиск и с вероятностью 0,3 обнаруживает бабочку, а с вероятностью 0,7 пропускает ее (для первой группы состояний); 2—летучая мышь определяет направление своего движения и расстояние до жертвы, причем с вероятностью 0,8 цель при этом не теряется; 3 — летучая мышь настигает бабочку и уничтожает ее с вероятностью 0,95. Что же может противопоставить преследователю бабочка? В чем заключаются ее действия? Будем рассматривать каждую группу состояний автомата как определенную

52

с

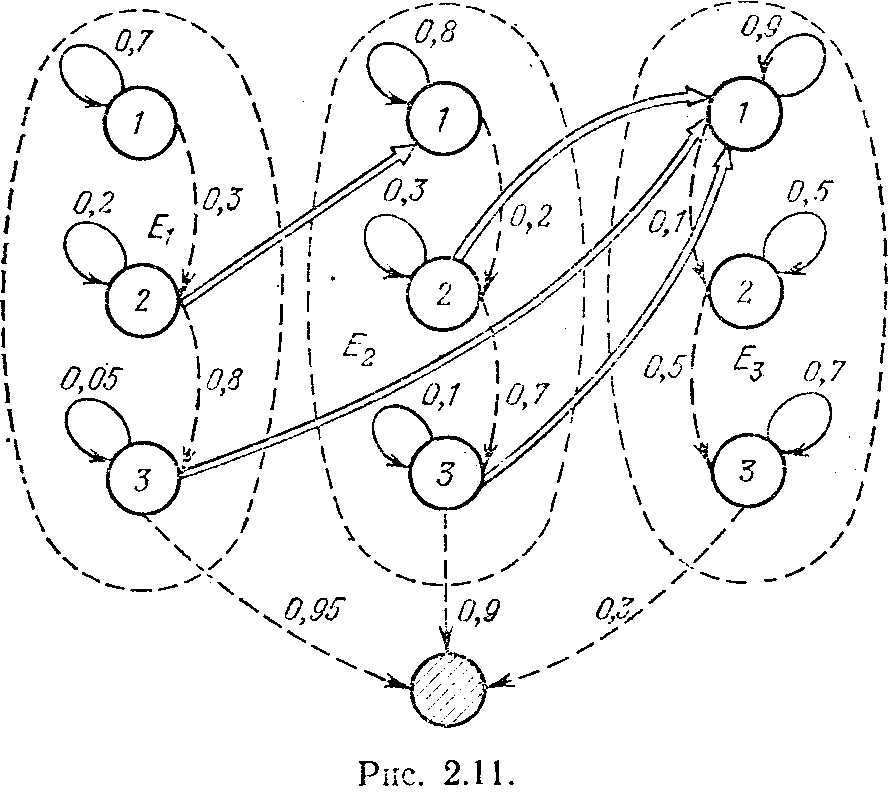
реду, задаваемую той стратегией бабочки, которой она придерживается. Трем группам состояний, показанных на рис. 2.11, можно, например, соотнести следующие стратегии: прямой полет (E1), пикирование или кабрирование (E2) и хаотическое движение (Ез). Действия бабочки сводятся к смене сред, переключению их. При этом бабочка может реализовать действие лишь в состояниях 2 и 3. На рис. 2.11 эти действия показаны двойными стрелками

переходов. В остальных состояниях бабочка выдает в среду нейтральный сигнал (другими словами, не меняет своих действий). После ухода от летучей мыши бабочка опять возвращается к движению по горизонтальной траектории, обеспечивающей ей возможность выполнения ее жизненного назначения — продолжения потомства. Эти переходы — действия на рисунке не показаны, чтобы не загромождать картину погони, которую мы анализируем.

В примере с ночной бабочкой и летучей мышью картина весьма прозрачна. Действия по переключению сред, показанные на рис. 2.11, позволяют бабочке максимально увеличить вероятность своего спасения. Однако в общем случае выбор оптимальной последовательности переключении, максимизирующей время жизни автомата, далеко не тривиален.

53

Пусть, например, как и в нашем примере, имеется три случайных среды, которые автомат может переключать своими действиями. И пусть имеется три обычных состояния и три поглощающих (летальных), в которых автомат погибает. Первые три мы, как и ранее, будем обозначать цифрами 1, 2, 3, а поглощающие состояния — цифрами 4, 5, 6. Вместо рисунка, подобного рис. 2.11, зададим три матрицы переходов автомата в трех возможных средах (табл 2.1)

Таблица 2.1

				Состо	ЯНИЯ
Среда	Состояния	1	2	3	4	5	6
	1	0,9			0,1
	2	0,95				0,05
Е1	3 4	0,8			1		0,2
	5					1
	6						¹
	1		0,9		0,1
	2		0,7			0,3
E2	3 4		0,95		1		0,05
	5					1
	6						1
	1			0,9	0,1
	2			0,92		0,08
E3	3 4			0,7	1		0,3
	5					1
	6						1

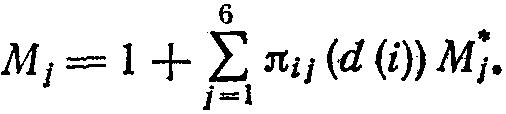
табл. 2.1 указаны только ненулевые значения переходных вероятностей Пиij. Если начальное состояние автомата есть i (i== 1, 2, 3), то время жизни автомата можно вычислить по формуле

Здесь М* — время жизни автомата с начальным состоянием j при оптимальном переключении им сред, d(i) — значение функции выхода автомата для состояния с номером i, т. е. номер той среды, на которую автомат переключает в этом состоянии текущую среду, Пиij(d(i)) — переходные вероятности смены состояний в среде с номером d(i). Очевидно, что оптимальное переключение d*(i) будет достигнуто тогда, когда будет получен maxМj для всех j (или max min Mj,

Мы не рассчитываем на то, что читатель будет в состоянии выдержать аналитические выкладки, лежащие в основе процедуры построения оптимального переключения. Отметим только, что такая процедура существует. И строго показано, что она позволяет автомату вероятностного типа осуществлять поиск оптимального способа переключения сред. Для подготовленного читателя укажем лишь на то, что, по сути своей, эта процедура есть модификация схемы динамического программирования Беллмана. Для нашего примера оптимальное переключение задается следующей функцией выхода: d{1)=3, d(2)==3, d(3)=2. При этом M3*= 15,47; М2*=15,23;

M1*=13,92. Общее время жизни автомата, выполняющего переключение сред, в полтора раза больше времени его жизни в пассивном режиме. А, значит, ночная бабочка совсем не зря тратит усилия на смену стратегии своего полета.

§ 2.7. От индивида к коллективу

Итак, мы познакомились с конструкциями зверушек, способных взаимодействовать с довольно сложно организованными средами. Правда, модели, которые мы обсудили, чрезвычайно упрощенно описывали это взаимодействие. Весьма бедным был ассортимент оценочных сигналов за действия, скудна информация, используемая для адаптации, примитивны средства организации взаимодействия со средой. Но к такому обеднению мы прибегли сознательно. Ибо нашей целью было показать, что, даже в условиях почти полного отсутствия информации о структуре поведения и о структуре среды, автономные подсистемы могут достигать поставленных перед ними целей. В последующих разделах книги мы время от времени будем «обогащать» зверушек, наделяя их более широкими возможностями, чем в данной главе. Однако основная Ваша цель—не исследование способностей подобных

65

устройств и эволюции их развития, а изучение поведения коллектива из таких устройств.

Нас будут интересовать проблемы взаимодействия зверушек между собой, организация их в сообщество, способное достигать общих целей, согласование личных целей участника сообщества с целью всего коллектива, распределение функций и ресурсов между совместно функционирующими участниками общего дела.

Прежде чем перейти к решению этих проблем, остановимся на той концептуальной схеме, которая будет лежать в основе всех наших дальнейших рассуждений. Читатель легко соотнесет ее с моделями, которые обсуждались нами в гл. 1 нашей книги. Эта модель изображена на рис. 2.12. Коллектив из

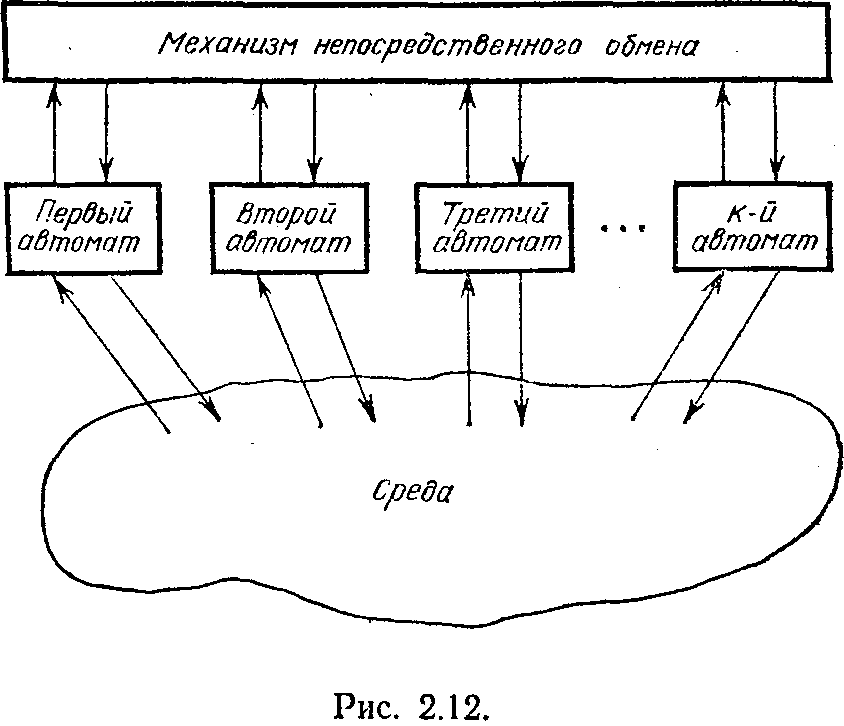
k автоматов взаимодействует со средой. Каждый из них делает это самостоятельно, не зная не только о действиях других членов коллектива, но и об их существовании. Для каждого автомата остальные участники коллектива как бы растворяются в среде, выступают по отношению к данному автомату как часть среды. Если в некотором такте взаимодействия автоматы зафиксировали свои действия, то среда воспринимает их как комбинированное воздействие, описываемое набором (di₁¹, di₂², ..., di_k^k), где верхний индекс указывает номер автомата в коллективе, а нижний — выбранное им действие. Среда может формировать оценочные сигналы на автомат либо на основании действий некоторой части или всех автоматов, либо на основании действий только данного автомата. Во втором случае коллектив разваливается и вся задача коллективного поведения сводится к рассмотрению k независимых друг от друга задач индивидуального поведения. Этот крайний случай не представляет интереса, и в дальнейшем мы его исследовать не будем. В первом же случае среда может как-то регулировать совместное воздействие автоматов и он представляет для нас принципиальный интерес.

Иногда мы будем рассматривать модели коллективного поведения, в которых, помимо среды, автоматы непосредственно общаются между собой. На рис. 2.12 эта возможность отражена в наличии некоторых специальных механизмов непосредственного обмена между автоматами, образующими коллектив.

И, наконец, вполне правомерно рассматривать все k автоматов и механизм непосредственного обмена (если он существует) как подсистемы некоторого организма, взаимодействующего со средой. Такая трактовка в ряде конкретных моделей будет нами использована в последующих главах книги.

Авторы чувствуют, что у читателя готовы сорваться с языка веские возражения против предлагаемой концептуальной модели взаимодействия в коллективе. Ограничение на общение между участниками коллектива кажется весьма надуманным и резко снижающим эффективность функционирования всей системы. Но мы еще раз подчеркиваем принципиальность этой схемы в рамках тех моделей, которым посвящена данная книга. В условиях невозможности полного обмена информацией о действиях, отсутствия центрального управляющего органа и резкого ограничения на время принятия решений по выбору действий предлагаемая модель все-таки оказывается, как будет видно из дальнейшего, вполне работоспособной.

Blog

Варшавский В. И., Поспелов Д. А

Содержание