Варшавский В. И., Поспелов Д. А

Вид материала

Документы

Содержание Г л а в а 4 КОГДА "ВСЕ ПО СПРАВЕДЛИВОСТИ"

Подобный материал:

• Герберт Александер Саймон Исследователи ии: Лотфи Заде Исследователи ии: А. А ляпунов,, 9.34kb.
• «Как привлечь средства государственных институтов развития» Варшавский Владислав Римович, 48.54kb.
• Аннотация к научно-образовательному материалу, 114.81kb.
• 141. Поспелов В. И., Стальнов В. С. Содружественная аккомодация глаз при дисбинокулярной, 167.36kb.
• Тезисы докладов участников III международного конгресса «Россия и Польша: память империй, 1372.37kb.
• Д. А. Поспелов, Г. С. Осипов, 487.33kb.
• Варшавский А. С. Следы на дне, 1828.32kb.
• Рабочая программа учебной дисциплины Для направления 080100. 62 «Экономика» (программа, 562.39kb.
• Диспут с Пирром: прп. Максим Исповедник и христологические споры VII столетия / Отв, 73.89kb.
• Программа дисциплины: Имитационные модели для направления Прикладная математика и информатика, 120.53kb.

§ 3.7. Еще три простые модели

D животном мире и мире растений неоднород­ность помогает регулировать соотношение тех или иных видов в биоценозах и фитоценозах. В качестве иллюстрации приведем две простенькие модели, хо­рошо известные в экологии.

На рис. 3.19,а показана ситуация, сложившаяся в среде, где живут бактерии, изображенные в виде овалов. В некоторые из них проникли частицы, назы­ваемые плазмидами. Эти органические образования стоят на грани живого и неживого. Плазмиды самовоспроизводятся и имеют обмен с внешней для них средой. Этой средой служат для них тела бактерий. В условиях неперенаселенности, когда бактерии име­ют достаточное количество пищи, плазмиды выделя­ют в окружающую их среду вещество, называемое иммунопротеином. На рис. 3.19, а плазмиды показаны зачерненными кружками, а иммунопротеин — точка­ми. Но вот количество бактерий увеличилось на

108

с
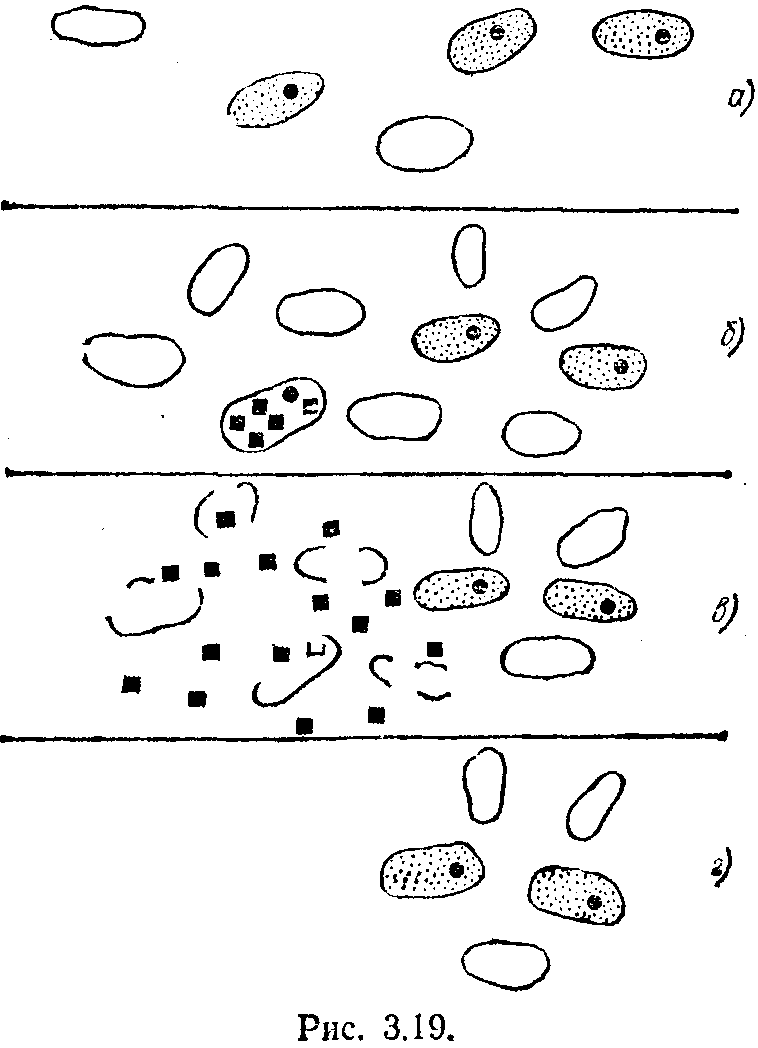
только, что они начинают испытывать голод. Голодают и плазмиды. Это приводит к тому, что плазмиды, оказавшиеся за граничным значением голодания, начинают вырабатывать не иммунопротеин, безвредный для бактерии-хозяина, а комицин. На рис. 3.19,6 показана такая ситуация, когда одна из плазмид начинает вырабатывать комицин (зачерненные квад­ратики в теле бактерии). Комицин убивает бактерию и плазмиду. Но комицин, попадая во внешнюю сре­ду, убивает в определенной окрестности все бактерии, не содержащие в своем теле иммунопротеин (рис. 3.19, б), после чего в среде остается уже мень­шее число бактерий (рис. 3.19,г), Если их все еще слишком много, то найдется такая плазмида, кото­рая опустится ниже «порога жизни" и начнет сра­батывать комицин, что приведет к дальнейшему со­кращению популяции бактерий. Плазмиды же де­лятся вместе с бактериями только тогда, когда пищи становится «слишком много", выше некоторого

109


порога, превышение которого вызывает деление у «чистых» бактерий.

Эту реальную модель саморегулирования численности организмов можно представить и в виде неод­нородного коллектива автоматов, живущего в некоторой среде, в которой поддерживается постоянный уровень пищи. Вся пища делится поровну между чле­нами коллектива. Автоматы - плазмидоносители делят­ся в том случае, когда количество поглощаемой ими пищи превышает некоторый порог Q₁. Остальные автоматы производят деление при более низком по­роге Q₂. Когда автомат - плазмидоноситель получает пищи меньше, чем Q₃ < Q₂, то он погибает и унич­тожает все обычные автоматы, которые находятся от него на определенном расстоянии (например, на торе в клетках, отстоящих от данной на расстоянии, не превышающем 5-кратного размера клетки). Для того чтобы одновременно не погибли все автоматы - плазмидоносители в модели, случайным образом выби­рается один из них. Если после этого уровень пищи все еще не превосходит Q₃, то случайным образом выбирается еще один автомат, способный уменьшить величину популяции. Моделирование такого процесса на ЭВМ показало почти точное совпадение процесса регулирования с тем, что происходит в природе у бактерий.

Вторая модель регулирования численности чуть-­чуть сложнее. Пусть члены коллектива могут исполь­зовать друг относительно друга при столкновениях (например, при случайных парных взаимодействиях) две стратегии: агрессивную и угрожающую. Если оба члены коллектива применяют агрессивную стратегию, то это напоминает драку двух петухов или схватку оленей. Оба противника наращивают усилия и не же­лают уступать друг другу. И лишь гибель или позор­ное бегство одного из них выявляет победителя. Если один из членов коллектива применяет агрессивную стратегию, а другой лишь угрожающую, то при дости­жении определенного уровня агрессивности тот, кто придерживался угрожающей стратегии, спасается бег­ством. Встреча собаки и кошки — яркий пример этой ситуации. Собака сначала всегда придерживается аг­рессивной стратегии, а кошка отвечает ей угрожаю­щей (выгибает спину, издает шипение и т. д.). Если собака пугается и переходит на угрожающую страте-

110

гию, то после взаимных угрожающих поз животные расходятся. Если же собака продолжает наращивать усилия в рамках агрессивной стратегии, то кошка спасается бегством.

Противники с самого начала могут оба придержи­ваться угрожающих стратегий. Они принимают раз­личные ритуальные угрожающие позы, и этот про­цесс продолжается до тех пор, пока один из них не признает себя побежденным (для этого он, как пра­вило, принимает специальную ритуальную позу под­чинения). Подобное соперничество можно наблюдать у собак, серых гусей, тетеревов и многих других животных.

Рассмотрим модель подобного соперничества. Агрессивную и угрожающую стратегии будем обо­значать соответственно буквами А и У. Составим таблицу, в которой оценены все возможные комбина­ции парного соперничества (табл. 3.6).

Таблица 3.6

		Вто	рой
		А	У
Первый	А	(-5, -5)	(+10, 0)
	У	(0, +10)	(+2, +2)

На пересечении строк и столбцов таблицы стоят пары чисел. Это условные оценки выигрышей — про­игрышей соперников при выборе той или иной стра­тегии поведения. Если, например, один из них (пер­вый) выбрал стратегию А, а второй — стратегию У, то первый получает выигрыш, равный 10 условным единицам, а второй остается при «своем интересе». Поясним теперь, как возникли эти оценки. Сначала мы условно оцениваем победу при соперничестве как выигрыш, равный +10, серьезное повреждение или гибель, которые могут произойти при наращивании усилий в стратегиях А, оцениваем как (—20). По­скольку при встрече двух агрессоров исход поединка мы считаем равновероятным, то математические ожидания поощрения — наказания при паре страте­гий (А,А) есть 0,5*10+0,5*(—20)= --5. Аналогич­но для встречи со стратегиями (У,У) это ожидание

111


вычисляется как 0,5*10+(—3)=2. Здесь оценка (—3) есть плата за нервное напряжение в длитель­ном конфликте при стратегии У. Эта стратегия приводит к значительному расходу нервных и других ре­сурсов животного. Таким образом, таб. 3,6 задает платежную матрицу некоторой игры.

Рассмотрим организм, который может по своему желанию менять свою стратегию в зависимости от обстоятельств. Этот организм можно смоделировать в виде автомата с двумя состояниями, соответствую­щими стратегиям А и У, использование которых оп­ределяется вероятностями Р_A и Ру. При этом, ко­нечно, Р_A+Ру=1. Рассмотрим коллектив, состоя­щий из подобных автоматов, и предположим, что он неоднороден, причем неоднородность задается раз­личными значениями Р_A. В частности, при Р_A==1 автомат является чистым агрессором. Он во всех случаях жизни придерживается стратегии А. При Р_A==0 автомат всегда придерживается стратегии У.

Как и в предшествующей модели, зададим неко­торые пороги Q1 и Q2. Если автомат накапливает выигрыш, превышающий Q1, то он «размножается». Вместо него появляются два автомата с тем же зна­чением Р_A у каждого. Если же накопленное нака­зание становится по абсолютной величине больше Q2, то автомат «вымирает». Возникает вопрос об оптимальном значении Р_A при случайном парном взаимодействии автоматов в коллективе. При моде­лировании на ЭВМ было показано, что коллектив из достаточно большого количества описанных автома­тов, в котором значения Р_A имели распределение, близкое к равномерному, эволюционирует в сторону однородного коллектива, для которого Р_A прибли­жается к значению 8/13. Из теории игр следует, что смешанная стратегия, при которой стратегии А и У выбираются с вероятностями 8/13 и 5/13, является для игрока в определенном смысле наилучшей. Она обеспечивает игроку максимально возможный гаран­тированный выигрыш (при самых наихудших для него действиях противника). Интересно было бы по­лучить экспериментальные данные из наблюдений за животными (например, кошками), которые давали бы оценки частоты выбора ими стратегий А и У при встрече с противником, равным по силе. К сожале­нию, такими данными мы не располагаем.

112

Вернемся к тому, с чего мы начали настоящую главу. События в Арбатове побудили нас рассмотреть ряд моделей коллективного взаимодействия и согла­шений. Эти модели, будь дети лейтенанта Шмидта образованными в области децентрализованного уп­равления, позволили бы им извлекать из участков куда больший доход, чем тот, которого они достигли. И в этом сила моделей, с которыми мы познако­мились.

В заключение укажем еще на одну модель рас­пределения участков, которой можно было бы вос­пользоваться при экспансии детей лейтенанта Шмид­та на территориях, на которых они никогда не быва­ли и сведений о которых у них нет. Такие участки кажутся равноценными, и распределение их вряд ли кого-нибудь взволнует. Жеребьевка их чисто фор­мальна. Но вот участники дележа разъехались на места и начали «работу». Через некоторое время они уже могут оценить средний доход с доставшегося им участка. Повторный съезд участников конвенции должен восстановить справедливость (например, за счет отступных или общей кассы). Но владельцам богатых участков этого не хочется. Они не альтруис­ты. Тогда можно использовать механизм направлен­ной лжи. При вопросе о среднем доходе с участка спрашиваемый говорит истинную цифру лишь тем, чей доход выше, или тем, кому невыгодно переходить на его участок. Остальным он врет, снижая истин­ный доход до того уровня, когда переход для спра­шивающего становится невыгодным. В этой модели участники должны располагать различной информа­цией о реальных доходах других участников.

При этом увеличение объема информация способ­ствует улучшению условий функционирования дан­ного автомата. Обратим внимание читателей на это важное свойство обсуждаемой модели. В модели рефлексивного поведения такая прямая зависимость не наблюдается.

Все модели, которые мы предложили в данной главе, обладают одной особенностью. Если рассмат­ривать коллектив автоматов как прообраз некоторой биологической, социальной или технической системы, то эта система функционирует в параллельном режи­ме, все ее подсистемы действуют независимо друг от друга и им не приходится ждать каких-либо

113


результатов работы других подсистем. Такое положение дел встречается не столь уж часто. В сложных системах работа подсистем часто взаимоувязана, су­ществуют определенные временные зависимости, отражающие порядок срабатывания подсистем. Эти зависимости могут носить как вероятностный, так и детерминированный характер. Поэтому в последую­щих двух главах мы рассмотрим децентрализованное управление, осуществляемое при таких дополнитель­ных ограничениях.


Г л а в а 4 КОГДА "ВСЕ ПО СПРАВЕДЛИВОСТИ"


«Мы холодны душой к нелепым чудесам.

И лишь возможное всегда по вкусу нам».

Буало


§ 4.1. Прав ли был Остап Бендер?

«..у окошечка администратора господствовало оживление. Там стояла цветная очередь. Молодые люди, в фасонных пиджаках и брюках того покроя, который провинциалу может только присниться, уверенно размахивали записочками от знакомых режиссеров, артистов, редакций, театрального костю­мера, начальника района милиции и прочих, тесно связанных с театром лиц, как то: членов ассоциации теа- и киноработников, общества «Слезы бедных ма­терей», школьного совета «Мастерской циркового эксперимента» и какого-то «Фортинбраса при УМСЛОПОГАСЕ». Человек восемь стояли с записка­ми от Эспера Эклеровича.

Остап врезался в очередь, растолкал фортинбрасовцев и, крича:—«Мне только справку, вы же ви­дите, что я даже калош не снял!», пробился к око­шечку и заглянул внутрь».

Прав ли был герой романа «Двенадцать стульев», когда считал, что с коротким делом можно проры­ваться без очереди, или великий комбинатор за­блуждался? Как должна была вести себя очередь? И как себя должен был вести администратор?

Очередь! Очередь становится таким же спутником нашего быта, как еда, сон, развлечения. Впрочем, как не вспомнить здесь очередь за едой в столовой, оче­редь за сном в гостинице, очередь за развлечением в театральной кассе. Временами нам кажется, что очередь является порождением чьей-то злой воли, ре­зультатом деятельности враждебных сил. Однако в действительности, возникновение очередей — такая же закономерность, как выпадение снега зимой и дождя летом. Плохая, неразумная организация не порождает очередь, а лишь увеличивает ее длину.

116


Понятие очереди безусловно предполагает нали­чие тех, кто в ней стоит. Заметим, что в очереди мо­гут стоять не только люди, а, например, коровы, ожидающие, когда их будут доить. Не только оду­шевленные предметы, а, например, радиоприемники, ожидающие починки, или месторождения полезных ископаемых, ожидающие, когда их разведают, а раз­веданные — когда их освоят. Очередь могут образо­вывать и объекты не материальной природы, напри­мер научные идеи, ожидающие, когда их разработа­ют и внедрят.

Объекты, стоящие в очереди, независимо от их природы, мы будем называть клиентами. При этом очередью мы будем именовать не всякую совокуп­ность клиентов, а лишь совокупность клиентов, свя­занных общей целью. Такой целью является стрем­ление быть обслуженным.

Обслуживание не обязательно должно быть ак­тивным. Например, без двух минут восемь вы вста­ли в очередь, чтобы расписаться в книге прихода на работу. Вы расписались, но «с точки зрения» очере­ди, эта книга обслужила вас

Весь комплекс обслуживающих средств: место обслуживания, обслуживающий персонал и т. п. в со­вокупности с правилами обслуживания мы будем на­зывать каналом обслуживания*).

Совокупность клиентов, каналов обслуживания и правил взаимодействия между клиентами и канала­ми, клиентов между собой и каналов между со­бой мы будем называть системой обслуживания.

Для изучения системы обслуживания мы должны знать, каким способом клиенты попадают в систему или каковы механизмы, или модели механизмов, по­рождающие у клиентов потребность в обслуживании. Должны знать, каковы характеристики процесса об­служивания. Должны знать, как организовано или как может быть организовано поведение клиентов в очереди и их взаимодействие друг с другом. Как клиенты попадают из очереди в канал обслуживания и как каналы обслуживания получают клиентов.

*) Для читателей, знакомых с терминологией теории массо­вого обслуживания, отметим, что введенное нами понятие «канал обслуживания» для классических моделей этой теории эквива­лентно понятию «обслуживающий прибор». Но наше понимание моделей обслуживания шире, чем в рамках упомянутой теории.

116

И, наконец, мы должны представлять себе возможные механизмы взаимодействия каналов обслужива­ния друг с другом как в процессе получения клиен­тов, так и в процессе их обслуживания.

У внимательного читателя может возникнуть сом­нение в логичности наших определений. С одной сто­роны, мы включаем клиентов в качестве элементов в систему обслуживания, а, с другой стороны, гово­рим, о том, что клиенты попадают откуда-то в эту систему. Но противоречие это чисто внешнее. Клиен­ты действительно попадают в систему обслуживания извне, но затем становятся ее элементами. И дрова в отопительной системе могут проиллюстрировать эту мысль.

Для организации управления в системе обслужи­вания мы, кроме правил поведения системы, с по­мощью которых можно осуществлять управление, должны также уметь оценивать качество функцио­нирования этой системы. Нетрудно понять, что здесь могут существовать явно противоречивые критерии, Как правило, в системах обслуживания критерий по­вышения рентабельности обслуживания вступает в противоречие с критериями качества обслуживания. Повышение рентабельности функционирования город­ского транспорта путем повышения загрузки транс­портных средств вряд ли будет встречено с понима­нием пассажирами. Именно противоречивость оценок качества функционирования делает системы обслу­живания наиболее интересными с точки зрения ор­ганизации в них оптимального управления.

Как клиенты поступают в систему? Самый простой способ — поступление клиентов через равные промежутки времени. Если время обслуживания меньше этого промежутка или равно ему, то очередь возникать не будет. Если же время обслуживания превышает интервал между появлениями клиентов, то очередь будет неограниченно возрастать.

Максимальное число клиентов, которое может об­служить канал за фиксированный отрезок времени, будем называть пропускной способностью канала. Доля времени, в течение которой система занята обслуживанием, будет определять нагрузку канала. При постоянном интервале поступления клиентов, или, как мы иногда будем говорить, поступлением заявок на обслуживание, и постоянном времени

117


обслуживания очередь не возникает, если нагрузка не превышает пропускной способности канала.

Если темп поступления клиентов или длитель­ность обслуживания подвергаются случайным коле­баниям, то очередь будет возникать всегда! Даже если пропускная способность системы больше, чем нагрузка. Очередь будет тем больше, чем больше разброс длительности интервала между поступления­ми клиентов и чем больше разброс длительности обслуживания. Очередь также возрастает по мере приближения нагрузки к пропускной способности системы. При приближении нагрузки к пропускной способности очередь начинает расти неограниченно. Зная, как характеристики очереди зависят от параметров системы, мы можем искать пути их измене­ния, приводящие, например, к уменьшению очереди.

Работая над гл. 3, мы в один из дней решили посмотреть кинофильм и начали звонить в ближай­ший кинотеатр, чтобы узнать репертуар и время на­чала сеансов. Телефон кинотеатра, как всегда, был непрерывно занят. Непрерывно набирая номер в те­чение 20 мин, мы наконец услышали:

— «Здравствуйте! Вам отвечает автоответчик кинотеатра «Прометей». Сегодня смотрите в нашем кинотеатре: на детском утреннике в 9 ч утра кино­фильм «Внимание, черепаха!». На сеансах 11 и 13 ч новая кинокомедия «Мимино». Новый художествен­ный фильм «Приезжая» на сеансах 15 ч, 16 ч 40 мин, 18 ч 30 мин, 20 ч 20 мин и 22 ч 10 мин. Приглашаем посетить наш кинотеатр. Наш адрес: проспект Про­свещения, д. 20». На часах было 16 ч, и нам каза­лось, что половину сообщения, которое мы прослу­шали, можно было бы опустить — нас мало интере­совало, что показывали в кинотеатре до 16 ч. Нам казалось, что можно было опустить также две пер­вых и предпоследнюю фразы — сокращение времени, необходимого для того, чтобы дозвониться до кино­театра, с лихвой компенсировало бы некоторое отсут­ствие избыточной вежливости в ответе. Мы взялись за карандаши.

Оказалось, что сокращение длительности текста, приводящее к увеличению пропускной способности, так изменяет отношение пропускной способности к нагрузке, что среднее время ожидания уменьшается почти в 5 раз. Нам, чтобы дозвониться до кинотеат-

118

pa, потребовалось бы 4 мин вместо 20 мин. Этот вы­игрыш оправдывает затраты на смену пленки в ав­тоответчике после начала каждого сеанса. Ведь если нам просто не повезло и среднее время, которое не­обходимо затратить, чтобы дозвониться в справочное бюро кинотеатра, равно не 20, а только 10 мин., то и в этом случае уменьшение вдвое времени обслужи­вания дает в час экономию около десяти человеко-часов, проведенных у телефона. Трудности ликвида­ции такого положения заключаются в том, что тысячи человеко-часов в месяц, затрачиваемые у теле­фонов в бесплодных попытках дозвониться в спра­вочные службы кинотеатров, дополнительные нагруз­ки на каналы телефонной связи и коммутационное оборудование телефонных станций ни в коей мере не влияют на оценку эффективности функционирования кинотеатров и их справочных служб. Аналогичные выводы, кстати, можно сделать о большинстве теле­фонных систем обслуживания, куда чрезвычайно сложно дозвониться.

Моральный и материальный ущерб, приносимый очередями людям, очевиден. Но, быть может, он не столь уж важен, если речь идет о неодушевленных предметах? К чему в этом случае сводится ущерб, приносимый очередью?

Во-первых, и это относится ко всем очередям не­зависимо от того, кто или что является клиентом, очередь должна где-то располагаться. Чем больше очередь, тем большего размера хранилища для кли­ентов следует создавать. Причем мы не можем ори­ентироваться на среднюю длину очереди — грубо го­воря, в половине случаев действительная очередь бу­дет больше средней. Создание помещений для рас­положения очереди (складов для хранения, стоящих в очереди изделии, буферной памяти для стоящих в очереди на обработку информационных массивов и т. п.) существенно удорожает системы обслуживания. В ряде случаев снижение объема хранилищ для оче­реди оправдывает расходы на введение дополнитель­ных каналов обслуживания.

Во-вторых, клиенты, стоящие в очереди, изъяты из употребления. Люди, стоящие в очереди в мага­зине, в это время не работают, не читают книги, не воспитывают своих детей. Автомобили, стоящие в очереди на ремонт, не перевозят грузы. Стоимость

119


всего, что стоит в очереди, входит в стоимость системы обслуживания. Если большой магистральный неф­тепровод заполнен нефтью, то эта нефть изъята из употребления и является составной частью нефтепровода, ее стоимость входит в стоимость нефтепровода, Так же и в системе обслуживания. Детали, стоящие в очереди на обработку, изъяты из употребления и в размере, равном средней длине очереди, входят в определение стоимости системы обработки. Среднее число автомашин, ожидающих своей очереди на ре­монт, является составной частью системы автосер­виса, и их стоимость входит в стоимость системы автосервиса.

Из сказанного ясно, что задача снижения средней длины очереди имеет явный экономический смысл.

Выше мы уже видели на примере, что среднюю длину очереди можно снизить, если уменьшить вре­мя обслуживания или, что эквивалентно, увеличить пропускную способность системы. Однако очень час­то мы не в состоянии влиять на этот параметр. Можем ли мы вместе с тем уменьшить среднюю длину очереди?

Выше уже говорилось, что система обслуживания, кроме всего прочего, характеризуется взаимодей­ствием клиентов в очереди, иначе говоря, договорен­ностью об их взаимном поведении в очереди. Такую договоренность мы будем называть дисциплиной об­служивания. Какие существуют дисциплины обслу­живания?

Самая привычная для нас дисциплина носит на­звание «первым пришел — первым обслужен». Это обычная, так называемая живая очередь. Существуют и экзотические дисциплины. Например,— последним пришел — первым обслужен. Смысл использования такой дисциплины может определяться различными соображениями, например конструкцией помещения для очереди. Порождающие указанную дисциплину хранилища для очереди называются мага­зином по аналогии с магазином для патронов в пис­толете. Отсюда и название «магазинная память» в вычислительных устройствах. Дисциплина «послед­ним пришел — первым обслужен» часто используется в системах противовоздушной обороны. Клиент (са­молет), появившийся последним в зоне обслужива­ния, имеет большую вероятность быть обслуженным

120

(сбитым), так как он дольше других клиентов (са­молетов) будет находиться в зоне обслуживания.

Дисциплины обслуживания предусматривают на­личие различных приоритетов, что разрешает клиен­ту нарушить основную дисциплину очереди. Типич­ный пример установленного приоритета — табличка:

«Инвалиды Отечественной войны обслуживаются без очереди». Приоритетные правила чрезвычайно раз­нообразны и каждый раз связаны с конкретными условиями функционирования системы. Если мы не можем изменять нагрузку на систему и характери­стики каналов обслуживания, т. е. их пропускную способность, то приоритетные правила остаются един­ственной возможностью вмешиваться в функциони­рование системы, т. е. управлять ее поведением. При этом возникают следующие вопросы. Существуют ли способы улучшить качество функционирования сис­темы за счет введения приоритетов? Если существу­ют, то какие характеристики системы могут быть улучшены и за счет каких приоритетов? Существуют ли способы организации коллективного поведения клиентов или каналов обслуживания, обеспечива­ющие выработку системы приоритетов, оптимизиру­ющей качество функционирования системы?

На все эти вопросы мы попытаемся ответить в следующих параграфах данной главы.